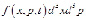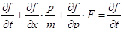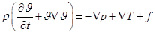Что требуется для перемещения потока в условиях турбулентности
Турбулентный режим движения жидкости
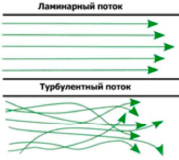
Движение жидкости, наблюдаемое при больших скоростях, называют турбулентный режим движения жидкости. В этом случае в движении жидкости нет видимой закономерности. Отдельные частицы перемешиваются между собой и движутся по самым причудливым все время меняющимся траекториям весьма сложной формы.
В этой статье подробно описывается процесс турбулентного режима, переход в турбулентный режим из ламинарного, формула и закон этого режима и многое другое.
Содержание статьи
Турбулентный режим движения в опытах
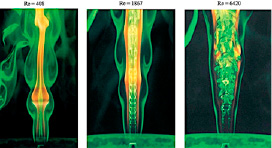
Для более конкретного представления турбулентного режима движения жидкости рассмотрим опыт Рейнольдса. Подробное описание здесь.
При добавлении краски в поток жидкости движущейся с небольшой скоростью красная краска будет двигаться ровной струйкой.
При увеличении скорости потока движение частиц так же увеличится. Струйка краски будет колебаться как на указано на рисунке.
При открытии крана и увеличении расхода через трубку, поток краски будет всё более интенсивнее перемешиваться с основным потоком жидкости, образуя всё больше вихрей.
Несмотря на кажущуюся беспорядочность движения частиц и изменения их скорости, величина средней скорости в достаточно большом промежутке времени остается постоянной.
Турбулентный режим движения жидкости всегда характеризуется пульсация скоростей. Под действием пульсации частицы жидкости, движущиеся в главном (осевом) направлении потока, получают, кроме того, так же и поперечные перемещения, вследствие чего между соседними слоями жидкости возникает обмен частицами, вызывающими непрерывное перемешивание жидкости.
Однако у стенок, ограничивающих поток, имеют место совсем иные, особые условия для движения жидкости. Наличие твердых границ делает поперечные движения частиц невозможными. Поэтому перемешивание жидкости здесь не происходит и частицы движутся по извилистым траекториям, почти параллельно стенкам.
Переход ламинарного режима в турбулентный
Все выше описанное позволяет установить следующую схему движения потока жидкости, обычно и принимаемую за основную рабочую схему при исследовании турбулентного режима.
По этой схеме у стенок образуется весьма тонкий слой, в котором движение жидкости происходит по законам ламинарного режима. Основная же центральная часть потока (ядро), связанная с этим слоем, называемым вязким (или ламинарным) подслоем, короткой переходной зоной, движется турбулентно с почти одинаковой для всех частиц жидкости средней скоростью.
Наличие вязкого (ламинарного) подслоя доказано экспериментально в результате весьма тщательных и точных измерений. Толщина этого слоя очень мала и обычно определяется долями миллиметра. Она зависит от числа Рейнольдса, и тем меньше, чем больше это число, т.е. чем больше турбулентность потока.
где d – диаметр трубы.
Из чего следует, что движение жидкости при турбулентном режиме течения должно всегда происходить со значительно большей затратой энергии, чем при ламинарном.
При ламинарном режиме энергия расходуется только на преодоление сил внутреннего трения между движущимися с различной скоростью соседними слоями жидкости. При турбулентном режиме, кроме этого, значительная энергия затрачивается на процесс перемешивания, вызывающий в жидкости дополнительные касательные напряжения.
Формула турбулентного режима течения
В старых теориях о турбулентном режиме принималось, что у стенок, ограничивающих поток, образуется некоторый неподвижный слой, по которому со значительными скоростями движется вся остальная масса жидкости.
Наличие этого неподвижного слоя с неизбежностью приводило к неправдоподобным выводам о “разрыве” скоростей, т.е. к такому закону распределения скоростей в поперечном сечении, при котором имеет место внезапное скачкообразное изменение скорости от нуля в неподвижном слое до конечной величины в остальной части потока.
Современные теории турбулентного режима течения исходят из схемы Л. Прандтля, который установил теоретический закон распределения скоростей в поперечном сечении потока.
По этому закону скорость в какой-нибудь точке сечения, например цилиндрической трубы, на расстоянии y от ее оси определяется формулой.
Для практического применения применяют выведенные из указанной выше формулы.
Для шероховатых труб
Для того, чтобы в трубе установилось распределение скоростей, соответствующее турбулентному режиму, жидкость должна пройти от входного сечения трубы некоторый определенный участок, называемый начальным участком турбулентного режима.
Длина этого участка определяется по формуле
Где d – диаметр трубы
Re – число Рейнольдса
Высказанные таким образом соображения о механизме движения и распределении скоростей в турбулентном потоке подтверждаются большим числом опытных данных. Из их рассмотрения следует, что при турбулентном режиме, как и нужно было ожидать, скорости распределяются по сечению более равномерно, чем при ламинарном режиме.
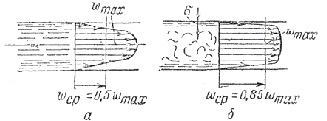
Для иллюстрации этого положения приведена картинка с нарисованными на ней кривыми распределения скоростей для потока жидкости в цилиндрической трубе при турбулентном режиме(сплошная линия) и при ламинарном режиме (пунктир).
При турбулентном режиме отношение средней скорости к максимальной осевой υср / υ0 изменяется от 0,75 до 0,90, в то время как при ламинарном режиме это отношении равно 0,5.
При этом следует иметь ввиду, что чем больше число Рейнольдса, т.е. чем интенсивнее происходит процесс перемешивания жидкости, тем больше будет это соотношение.
Видео по теме
Турбулентность наступает после превышения некоторого критического значения числа Рейнольдса, но в некоторых случаях она может возникнуть самопроизвольно.
Например, в случае перепада давления когда соседние области потока движутся рядом или проникают одна в другую, при воздействии силы тяжести или когда жидкая среда обтекает непроницаемую поверхность.
Математики доказали универсальный закон турбулентности
Используя случайные процессы, три математика доказали элегантный закон, лежащий в основе хаотического движения турбулентных систем
Представьте себе спокойную реку. А теперь представьте быстрый поток пенящейся воды. Какая между ними разница? Для математиков и физиков она состоит в том, что спокойная река течёт в одном направлении, а бурный поток – в нескольких направлениях сразу.
Физические системы с таким бессистемным движением называют турбулентными. Из-за того, что их движение имеет одновременно столько характеристик, их очень сложно изучать математически. Сменится не одно поколение математиков до тех пор, пока исследователи научатся описывать бурную речку точными математическими выражениями.
Однако новое доказательство говорит о том, что хотя некоторые турбулентные системы и кажутся непокорными, на самом деле они подчиняются одному универсальному закону. В этой работе приводится одно из самых строгих описаний турбулентности, когда-либо данных математикой. И появляется оно благодаря новому набору методов, которые сами по себе меняют процесс изучения исследователями этого доселе непокорного явления.
«Возможно, это самый многообещающий подход к турбулентности», — сказал Владимир Сверак, математик из Миннесотского университета, эксперт по турбулентности.
В новой работе даётся способ описания закономерностей, возникающих в движущихся жидкостях. Их хорошо видно на примере резких колебаний температуры у соседних точек океанов или завораживающих картинах, получающихся при смешивании чёрной и белой красок. В 1959 году австралийский математик Джордж Бэтчелор предсказал, что у этих закономерностей есть точный и регламентируемый порядок поведения. Новое доказательство подтверждает истинность «закона Бэтчелора», как назвали это предсказание.
«Закон Бэтчелора можно увидеть повсюду», — сказал Джейкоб Бедроссиан, математик из Мэрилендского университета в Колледж-Парке, соавтор доказательства совместно с Алексом Блументалем и Сэмюэлем Паншон-Смитом. «Доказав этот закон, мы смогли лучше осознать его универсальность».
Турбулентность сверху донизу
И хотя в новом доказательстве описываются не совсем такие же процессы, какие происходят в бурном течении реки, они близко связаны с ними и достаточно знакомы нам. Поэтому давайте для начала представим их себе, перед тем, как перейти к турбулентности особого типа, которую анализировали математики.
Представьте себе кухонную раковину, полную воды. Вода начинает вращаться в раковине практически как единая масса. Если мы увеличим жидкость и измерим её скорость на более мелких масштабах, мы увидим то же самое – каждая микроскопическая часть жидкости движется в согласии с остальными.
«Движение в основном завязано на масштаб всей раковины», — сказал Блументаль, постдок из Мэрилендского университета в Колледж-Парке.

Алекс Блументаль, постдок из Мэрилендского университета в Колледж-Парке
Теперь представьте, что вместо того, чтобы просто дать воде стечь, выдернув пробку, вы добавили в раковину водяные струи, закручивающие её, как в джакузи. Невооружённым взглядом можно будет уловить множество возникающих в воде водоворотов. Выберем один из них и увеличим его масштаб. Если бы вы были математиком, пытающимся анализировать потоки турбулентной раковины, вы могли бы надеяться, что каждая частица воды в выбранном водовороте двигается в одном и том же направлении. Это сильно облегчило бы работу моделирования жидкости.
Но, увы, вы обнаружите, что сам водоворот состоит из множества маленьких водоворотиков, каждый из которых движется особым образом. Увеличьте его изображение, и вы вновь увидите, что и он в свою очередь состоит из различных водоворотов, и так далее, вплоть до самых мелких масштабов, пока эффекты внутреннего трения (или вязкости) жидкости не возьмут вверх и не сгладят потоки.
Это явный признак турбулентных систем – различное поведение вложенных одна в другую подсистем на разных масштабах. Чтобы полностью описать движение турбулентной системы, придётся описать происходящее на всех этих масштабах в любой момент времени. Ни один из них не получится проигнорировать.
Это серьёзное требование – оно похоже на моделирование траекторий движения бильярдных шаров, учитывающее абсолютно всё, от движения Земли по Галактике, до взаимодействия молекул газа с шарами.
«Пришлось учитывать всё и сразу, из-за чего эту задачу так невероятно сложно моделировать», — сказал Жан-Люк Тиффо из Висконсинского университета, изучающий турбулентность.
В итоге математики десятилетиями пытались создать описание турбулентности, точно описывающее происходящее в каждой точке турбулентной системы в каждый момент времени. И не добились успеха.
«Турбулентность слишком сложна для того, чтобы атаковать её в лоб», — сказал Тиффо. Это верно для бурных рек и раковин с вытекающей жидкостью. Это верно и для особого варианта турбулентности, используемого в новом доказательстве.
Перемешивание
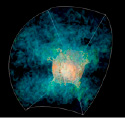
Раковина и река – примеры гидродинамической турбулентности. Они турбулентны в том смысле, что векторы скорости жидкости – направления и скорости движения частиц – сильно варьируются от точки к точке. Новая работа описывает другие свойства жидкости кроме векторов скорости, которые можно измерить в каждой её точке. Чтобы понять, что это означает, представим себе смешивание красок.
Начнём с банки белой краски. Будем добавлять чёрную по одной капле в секунду, помешивая краску. Первая капля упадёт в белую краску и будет выделяться, как островок. Но вскоре она начнёт растворяться в белой краске, вытягиваясь во всё более тонкие линии. Последующие капли чёрной краски будут находиться на разных стадиях того же преображения: растягиваться, удлиняться, вливаться в краску, которая постепенно превращается в серую.
Как векторы скорости меняются от точки к точке в раковине, где перемешивают воду, так и концентрация чёрной краски в белой будет меняться от точки к точке при перемешивании: в некоторых местах её концентрация будет больше (более толстые линии), в некоторых – меньше.
Такой вариант является примером «пассивной скалярной турбулентности». Она возникает при вливании одной жидкости, «пассивного скаляра», в другую – молоко в кофе, чёрную краску в белую.
Пассивная скалярная турбулентность также описывает многие явления природы – резкие перепады температуры между близкими точками океана. В такой среде океанские течения «смешивают» температуры так же, как перемешиваются чёрная и белая краски.
Закон Бэтчелора предсказывает соотношение количества крупномасштабных явлений (толстых завитков краски или потоков океанской воды одинаковой температуры) к количеству явлений на меньших масштабах (тонких линий краски) при смешивании жидкостей. Законом его называют потому, что физики уже много лет наблюдают это явление в экспериментах.
«С точки зрения физики этого достаточно, чтобы назвать его законом», — сказал Паншон-Смит, математик из университета Брауна. Однако до этой работы не существовало математического доказательства его непременного выполнения.

Закон Бэтчелора предсказывает соотношение количества крупномасштабных явлений (толстых завитков краски или потоков океанской воды одинаковой температуры) к количеству явлений на меньших масштабах (тонких линий краски) при смешивании жидкостей. Это соотношение остаётся неизменным при изменении масштабов, так, как маленькие матрёшки сохраняют пропорции большой.
Чтобы осознать идею Бэтчелора, вернёмся к краске. Представьте, что вы некоторое время продолжаете этот эксперимент, добавляя капли чёрной краски и помешивая. Теперь остановим время. Вы увидите толстые полоски чёрной краски (её замешивали меньше всего), более тонкие полоски (их замешивали дольше), и ещё более тонкие (их замешивали ещё дольше).
Закон Бэтчелора предсказывает, что количество толстых полосок, более тонких и совсем тонких полосок подчиняется точной пропорции – примерно как матрёшки подчиняются одинаковым пропорциям.
«В заданном фрагменте жидкости видны полоски разных масштабов, потому что часть капель только начала замешиваться, а часть замешивается уже некоторое время, — сказал Блументаль. – Закон Бэтчелора описывает распределение размеров полосок чёрной краски». Точную пропорцию описать в двух словах трудно, однако более тонких полосок получается больше, чем толстых, причём в определённое количество раз.
Закон предсказывает, что пропорция сохраняется даже если посмотреть на фрагмент жидкости с увеличением. У полосок различной толщины, как в небольшом участке жидкости, так и во всей банке будет ровно то же соотношение по количеству; и увеличивая масштаб, мы будем видеть то же самое соотношение. Закономерность одна на всех масштабах, как в гидродинамической турбулентности, где в каждом водовороте есть маленькие водоворотики.
Довольно смелое предсказание, которое, к тому же, сложно смоделировать математически. Сложная вложенность явлений на разных масштабах не даёт возможности точно описать появление закона Бэтчелора в едином потоке жидкости.
Но авторы работы придумали, как обойти эту сложность и доказать его.
Случайный подход
Бедроссиан, Блументаль и Пуншон-Смит применили подход, рассматривающий среднее поведение жидкостей во всех турбулентных системах. Математики и раньше пробовали эту стратегию, но ни у кого не вышло успешно её реализовать.
Этот подход работает потому, что случайность иногда позволяет делать точные предсказания поведения системы. Представьте себе вертикальную доску, утыканную гвоздями. Уроните вдоль неё монетку сверху, и она будет отскакивать от гвоздей, пока не попадёт в одну из щелей внизу. Сложно предсказать, куда попадёт конкретная монетка –слишком много факторов влияет на то, куда она будет отскакивать после каждого столкновения.

Сэмюэл Пуншон-Смит
Вместо этого можно рассматривать систему как случайную – и что для каждого гвоздя есть шансы, что монетка отскочит как вправо, так и влево. Если правильно подсчитать вероятности, то можно будет делать точные предсказания о поведении системы в целом. К примеру, можно обнаружить, что монетки с большей вероятностью будут попадать в конкретные щели.
«Что хорошо со случайностью, так это возможность делать усреднения, — сказал Тиффо. – Усреднение – очень надёжная идея, в том смысле, что её не касаются многие мелкие детали».
Что это означает для турбулентности и смешивания красок? Поскольку точные и детерминистские утверждения находятся за пределами возможности математики, полезнее будет представлять, что на краску действуют некие случайные силы – иногда мешающие её сюда, иногда туда, безо всякой закономерности. Такой подход называют случайным, или стохастическим. Он позволяет математикам использовать статистические выкладки высокого уровня и изучать, что происходит в системах в целом, не зарываясь в специфику каждой детали.
«Немного случайности позволяет победить сложности», — сказал Пуншон-Смит.
Именно это, наконец, позволило трём математикам доказать закон Бэтчелора.
Понимание смешивания
Один из способов доказать физический закон – представить себе условия, которые бы его аннулировали. Если можно доказать, что такие условия не возникают, это докажет, что закон всегда работает. Команда поняла, что для того, чтобы избежать предсказываемых законом Бэтчелора закономерностей, у замешивания должны быть совершенно определённые характеристики.
Доказательство закона разделено на четыре работы, опубликованные в онлайне между сентябрём 2018 и ноябрём 2019. Первые три концентрировались на понимании определённых движений смешиваемой краски, которые не позволили бы сработать закону Бэтчелора, и исключении таких движений. Они доказали, что даже если бы вы взяли жидкость, специально созданную так, чтобы победить закон Бэтчелора, закономерность в ней всё равно бы проявилась.
«Главное, что нужно понять – это что жидкость не может замыслить ничего против вас», — сказал Бедроссиан.

Джейкоб Бедроссиан
К примеру, закон Бэтчелора не сработал бы, если бы процесс смешивания приводил к появлению стойких водоворотов, или воронок, в краске. Такие воронки удерживали бы некоторые капли чёрной краски на одном месте – как обломки на краю потока – и краска бы не смешивалась.
«В таком водовороте траектории частиц будут не хаотичными; они не разделяются быстро, а крутятся все вместе, — сказал Бедроссиан. – Если ваша система не смешивает краски с правильной скоростью, закон Бэтчелора не проявится».
В первой работе математики сконцентрировались на том, что происходит во время процесса смешивания с двумя точками чёрной краски, изначально находившимися рядом друг с другом. Они доказали, что точки следуют случайными путями и расходятся в разных направлениях. Иначе говоря, близко расположенные точки не могут застрять в водовороте, который бы удерживал их вместе всё время.
«Изначально частицы движутся вместе, — сказал Блументаль, — но в итоге разделяются и расходятся по совершенно разным направлениям».
Во второй и третьей работах они шире взглянули на процесс смешивания. Они доказали, что в хаотической жидкости в общем случае чёрная и белая краска смешиваются с максимально возможной скоростью. Затем они определили, что в турбулентной жидкости не формируются локальные несовершенства (водовороты), которые бы могли помешать появлению элегантной глобальной картины, описанной законом Бэтчелора.
В первых трёх работах авторы проделали сложные математические выкладки, необходимые для доказательства того, что краска смешивается тщательно и хаотично. В четвёртой они показали, что в жидкости с такими свойствами смешивания закон Бэтчелора возникает как необходимое следствие.
Это одно из наиболее сильных математически строгих утверждений, касающихся турбулентных систем. Что ещё важнее, оно открывает нам возможности для нового потока математических идей. Турбулентность – явление хаотичное, почти случайное в своём движении. Три математика придумали, как бороться со случайностью при помощи случайности. Другие специалисты в этой области почти наверняка последуют за ними.
«Их большой вклад состоит в том, чтобы предоставить нам платформу, на которой можно строить доказательства, — сказал Тиффо. – Думаю, случайность – один из немногих способов построения модели турбулентности, которую мы способны понять математически».
Что требуется для перемещения потока в условиях турбулентности
Данная статья является реферативным изложением основной работы. Полный текст научной работы, приложения, иллюстрации и иные дополнительные материалы доступны на сайте V Международного конкурса научно-исследовательских и творческих работ учащихся «Старт в науке» по ссылке: https://school-science.ru/5/11/33832
Турбулентные процессы наверняка ощущал каждый, кто хотя бы пару раз летал на самолете. Иногда она почти не заметна, а иногда становится причиной травм пассажиров и серьезных повреждений техники. Как сообщает Федеральное Агентство по гражданской авиации США (FAA), за год более 1000 человек получают травмы во время перелетов из-за турбулентности. Турбулентность неблагоприятно действует на навигационные приборы, вызывая помехи, а порой и повреждения. Ученые придумывают все новые способы, как ослабить это явление. Но существуют случаи, когда турбулентность играет на руку человеку. Один из примеров таких случаев меня и заинтересовал. Это смешивание топлива в двигателях в турбулентных потоках. В этом случае турбулентность помогает в убыстрении процесса смешивания, а как следствие и горения.
Увеличение скорости получения горючей смеси и ее горения одна из важнейших задач современного инженера. Поэтому использование турбулентности весьма актуально. Подробнее о турбулентности и ее применении в строении двигателей я расскажу в своем проекте.
1. Что такое турбулентность?
При определенных параметрах турбулентность наблюдается в потоках жидкостей и газов, многофазных течениях, жидких кристаллах, квантовых бозе- и ферми- жидкостях, магнитных жидкостях, плазме и любых сплошных средах (например, в песке, земле, металлах). Турбулентность также наблюдается при взрывах звезд, в сверхтекучем гелии, в нейтронных звездах, в легких человека, движении крови в сердце, при турбулентном (т. н. вибрационном) горении.
Турбулентность возникает самопроизвольно, когда соседние области среды следуют рядом или проникают один в другой, при наличии перепада давления или при наличии силы тяжести, или когда области среды обтекают непроницаемые поверхности. Она может возникать при наличии вынуждающей случайной силы. Обычно внешняя случайная сила и сила тяжести действуют одновременно. Например, при землетрясении или порыве ветра падает лавина с горы, внутри которой течение снега турбулентно.
Мгновенные параметры потока (скорость, температура, давление, концентрация примесей) при этом хаотично колеблются в округ средних значений. Зависимость квадрата амплитуды от частоты колебаний (или спектр Фурье) является непрерывной функцией.
Турбулентность – явление, заключающееся в том, что, обычно, при увеличении скорости течения жидкости или газа в среде самопроизвольно образуются многочисленные нелинейные фрактальные волны и обычные, линейные различных размеров, без наличия внешних, случайных, возмущающих среду сил и/или при их присутствии. Для расчета подобных течений были созданы различные модели турбулентности. Волны появляются случайно, и их амплитуда меняется хаотически в некотором интервале. Они возникают чаще всего либо на границе, у стенки, и/или при разрушении или опрокидывании волны. Они могут образоваться на струях. Экспериментально турбулентность можно наблюдать на конце струи пара из электрочайника.
Турбулентность в ее обычном понимании возникает в пристеночных слоях слабовязких жидкостей или газов либо на некотором удаленном расстоянии за плохообтекаемыми телами. Скорее всего, турбулентность описывается уравнением Больцмана, поскольку характерные масштабы этого уравнения намного меньше масштабов турбулентности.
Уравнение Больцмана описывает эволюцию во времени (t) функции распределения плотности f(x, p, t) в одночастичном фазовом пространстве, где x и p – координата и импульс соответственно. Распределение определяется так, что
пропорционально числу частиц в фазовом объеме d³x d³p в момент времени t. Уравнение Больцмана
Здесь F(x, t) – поле сил, действующее на частицы в жидкости или газе, а m – масса частиц. Слагаемое в правой части уравнения добавлено для учета столкновений между частицами.
Но вопрос остается открытым, в настоящее время ведутся исследования о применимости этого уравнения для моделирования процесса возникновения турбулентности. Чаще всего в качестве математического описания турбулентности используют уравне́ния Навье́ – Сто́кса это – система дифференциальных уравнений в частных производных, описывающая движение вязкой ньютоновской жидкости. Уравнения Навье – Стокса являются одними из важнейших в гидродинамике и применяются в математическом моделировании многих природных явлений и технических задач. Названы по имени французского физика Анри Навье и британского математика Джорджа Стокса.
Однако до настоящего момента не получено ни одного точного аналитического решения этой системы уравнений для турбулентной области течения. Проблема заключается в том, что уравнения движения жидкости (уравнения Навье-Стокса) являются безмасштабными, то есть сами по себе не задают пределов прямого каскада и таким образом не определяют характерного размера (масштаба) турбулентных вихрей. Тем не менее, на их основе разработано огромное множество математических моделей турбулентности (RANS, LES, DES и DNS модели). Эти модели, за исключением модели DNS, широко используются для инженерных расчетов. В случае несжимаемой жидкости система состоит из двух уравнений:
В гидродинамике обычно уравнением Навье – Стокса называют только одно векторное уравнение движения. Впервые уравнение Навье – Стокса было получено Навье (1822, несжимаемая жидкость) и Пуассоном (1829, сжимаемая жидкость), которые исходили из модельных представлений о молекулярных силах. Позже феноменологический вывод уравнения был дан Сен-Венаном и Стоксом. Обычно турбулентность наступает при превышении критической величины неким параметром, например числом Рейнольдса или Релея (в частном случае скорости потока при постоянной плотности и диаметре трубы и/или температуры на внешней границе среды). Количественные условия перехода к турбулентности были экспериментально открыты английским физиком и инженером О. Рейнольдсом в 1883 году при изучении течения воды в трубах. Число Рейнольдса – величина, характеризующая отношение нелинейного и диссипативного членов в уравнении Навье – Стокса. Число Рейнольдса 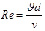
2. Смешивание и горение
в турбулентном потоке
Турбулентность, например, можно создать, если:
• увеличить линейную скорость или угловую скорость вращения потока, размер обтекаемого тела, уменьшить первый или второй коэффициент молекулярной вязкости, увеличить плотность среды;
• увеличив угловую скорость вращения или радиальный градиент
• задав очень сложный вид внешней силы (примеры: хаотичная сила, удар). Течение может не иметь фрактальных свойств.
• создав сложные граничные или начальные условия, задав функцию формы границ. Например, их можно представить случайной функцией. Например: течение при взрыве сосуда с газом. Или организовать вдув газа в среду, создать шероховатую поверхность. Использовать разгар сопла. Поставить сетку в течение. Течение может при этом не иметь фрактальных свойств.
• облучив среду звуком высокой интенсивности.
• с помощью химических реакций, например горения. Форма пламени, как и вид водопада может быть хаотичной.
Рассмотрим более подробно последний аспект возникновения турбулентности в процессе сгорания топлива в тепловых двигателях, который непосредственно связан с запуском летательных аппаратов. Тепловой двигатель – устройство, преобразующее внутреннюю энергию топлива в механическую энергию. К тепловым двигателям относятся: паровая машина, двигатель внутреннего сгорания, паровая и газовая турбины, реактивный двигатель. Их топливом является твердое и жидкое топливо, солнечная и атомная энергии.
Горение топлива в тепловых двигателях обычно происходит в сильно турбулизованном потоке. Турбулентный поток характеризуется неупорядоченным движением частиц газа, при котором скорость в каждой точке потока меняется по направлению и по величине. Для турбулентного потока характерно наличие пульсаций скорости, давления, температуры и концентрации вещества.
Молекулярный механизм передачи тепла и массы вещества интенсифицируется пульсациями и перемешиваниями отдельных объемов газовой смеси. В мелкомасштабных молях происходит быстрый процесс молекулярного перемешивания, в частности происходит перемешивание продуктов сгорания со свежей смесью. В тех молях, где получающаяся после смешения температура достаточно высока, смесь успевает сгореть по законам объемной реакции раньше, чем в таком медленном процессе, как ламинарное горение. Образующиеся при этом продукты реакции опять смешиваются с молями свежей смеси и, таким образом, происходит распространение пламени. В тех молях, где температура после смешения слишком мала, реакция горения за время существования моля не успевает завершиться. Кроме того, в зоне горения должны также существовать моли, состоящие только из свежей смеси или только из продуктов реакции и в данный момент не участвующие в горении. Можно предполагать, что суммарная скорость горения в этом случае будет значительно превышать скорость ламинарного горения, так как молекулярно-турбулентное смешение происходит с большей скоростью, чем ламинарное. Ламинарное течение – течение, при котором жидкость или газ перемещается слоями без перемешивания и пульсаций (то есть без беспорядочных быстрых изменений скорости и давления).
Скорость распространения пламени зависит также от состояния смеси перед воспламенением. Если смесь неподвижна или течет ламинарно, то процессы переноса во фронте пламени осуществляются за счет молекулярной диффузии и теплопроводности. Такое распространение пламени называют ламинарным. Если горючая смесь находится в турбулентном движении, то молекулярная диффузия начинает играть второстепенную роль – ведущее значение в распространении пламени приобретают процессы турбулентного смешения свежей смеси с продуктами сгорания. Подобное горение называют турбулентным.
Смесители для жидкостей работают преимущественно по механизму ламинарного смешения, сопровождающегося увеличением площади поверхности раздела между компонентами и распределением элементов поверхности раздела внутри объема смесителя. Конструкция такого смесителя зависит от вязкости смесей. Например, для низковязких жидкостей применяют лопастные и высокоскоростные диспергирующие смесители. При малой вязкости смеси существенную роль может играть турбулентное смешение. Для смесей со средними значениями вязкости используют разнообразные двухроторные смесители, например смеситель с 2-образными роторами. Такой смеситель представляет собой камеру, образованную двумя полуцилиндрами. В камере установлены два ротора, вращающиеся навстречу друг другу с различной скоростью. Обычно отношение скоростей вращения роторов составляет 2/1. Смешение происходит вследствие взаимного наложения тангенциального и осевого движений материала. Чтобы исключить возможность образования застойных зон, зазор между роторами и стенкой камеры делают небольшим – около 1 мм. Такие смесители используют для смешения жидкостей с вязкостью 0,5—500 Па-с. К двухроторным относятся также смесители с зацепляющимися роторами, вращающимися с одинаковой скоростью. Двухроторные смесители широко используют для изготовления наполненных пластмасс, а также для смешения различающихся по вязкости жидкостей и паст.
3. Различные подходы в описании турбулентности
Для теоретического описания турбулентности применяются различные подходы. При статистическом подходе считается, что турбулентность порождает случайно изменяющаяся совокупность вихревых элементов различных размеров. Другим подходом является метод спектрального анализа, который дополняет статистический подход.
При больших числах Рейнольдса, скорости потока от небольших изменений на границе зависят слабо. Поэтому при разных начальных скоростях движения корабля формируется одна и та же волна перед его носом, когда он движется с крейсерской скоростью. Нос ракеты обгорает и создается одинаковая картина разгара, несмотря на разную начальную скорость.
4. Фрактальное представление турбулентности
Прежде чем говорить о фрактальном представлении волн турбулентности, надо упомянуть, что же такое фрактал. Фрактал – это математическое множество, обладающее свойством самоподобия. Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке в результате изучения непрерывных недифференциируемых функций (например, функция Больцано, функция Вейерштрасса, множество Кантора). Термин «фрактал» введен Бенуа Мандельбротом в 1975 году и получил широкую известность с выходом в 1977 году его книги «Фрактальная геометрия природы». Особую популярность фракталы обрели с развитием компьютерных технологий, позволивших эффектно визуализировать эти структуры.
Слово «фрактал» употребляется не только в качестве математического термина. Фракталом может называться предмет, обладающий, по крайней мере, одним из указанных ниже свойств:
• Обладает нетривиальной структурой на всех масштабах. В этом отличие от регулярных фигур (таких как окружность, эллипс, график гладкой функции): если мы рассмотрим небольшой фрагмент регулярной фигуры в очень крупном масштабе, то он будет похож на фрагмент прямой. Для фрактала увеличение масштаба не ведет к упрощению структуры, то есть на всех шкалах мы увидим одинаково сложную картину.
• Является самоподобным или приближенно самоподобным.
• Обладает дробной метрической размерностью или метрической размерностью, превосходящей топологическую.
Многие объекты в природе обладают свойствами фрактала, например: побережья, облака, кроны деревьев, снежинки, кровеносная система, система альвеол человека или животных.
Увидеть турбулентность крайне сложно без специального оборудования, но можно прибегнуть к компьютерному моделированию и использовать фрактальную структуру турбулентности. Турбулентный вихрь сам состоит из подобных ему завихрений. Используя язык программирования Java, я попытался создать модель турбулентного фрактального вихря (см. полный текст работы. ПРИЛОЖЕНИЕ 1). За основу взял дугу полуокружности 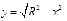
На середине каждой дуги был построен еще один «вихрь», а на серединах новых «вихрей» следующие. В итоге после одной итерации получаем 15 вихрей, в результате второй 225, после третьей 153 и т.д. В результате имеем следующий фрактал, который визуально напоминает «вихрь» или воронку, а сам он состоит из таких же самоподобных вихрей.
Заключение
Исследования турбулентных течений, этой все еще наиболее трудной проблемы гидродинамики, продолжают приносить важные технологические достижения, однако путь к прогрессу здесь никак не назовешь прямым. История исследований турбулентных течений научными методами насчитывает приблизительно сто лет, и на протяжении этого периода времени некоторые из наиболее великих умов в области физики, механики и техники пробовали иногда свои силы в решении имеющихся здесь проблем. Было достигнуто продвижение вперед по многим направлениям исследований, и в итоге мы видим действительно заметный прогресс в наших знаниях о предмете. Тем не менее «проблема турбулентности» в целом, что бы она ни означала, все еще сохраняется. С точки зрения теории новый интерес к идеям распространения вихрей в невязкой жидкости и кинематике вихревых взаимодействий оказывается неслучайным. Заслуживает внимания и вопрос о естественных или неустранимых вихревых образованиях. Наиболее важным аспектом существования в турбулентном потоке детерминированных структур является возможность воздействия на турбулентность путем прямой интерференции этих крупномасштабных структур. Такое воздействие могло бы привести к очень важным для техники достижениям. Турбулентность и теперь, и в будущем останется одной из наиболее трудных проблем гидродинамики, и имеющийся здесь опыт позволяет предположить, что последующее падение интереса к когерентным структурам более чем вероятно. Итоговый рост наших знаний о турбулентности может оказаться ниже уровня сегодняшних больших ожиданий, но в любом случае он будет положительным.