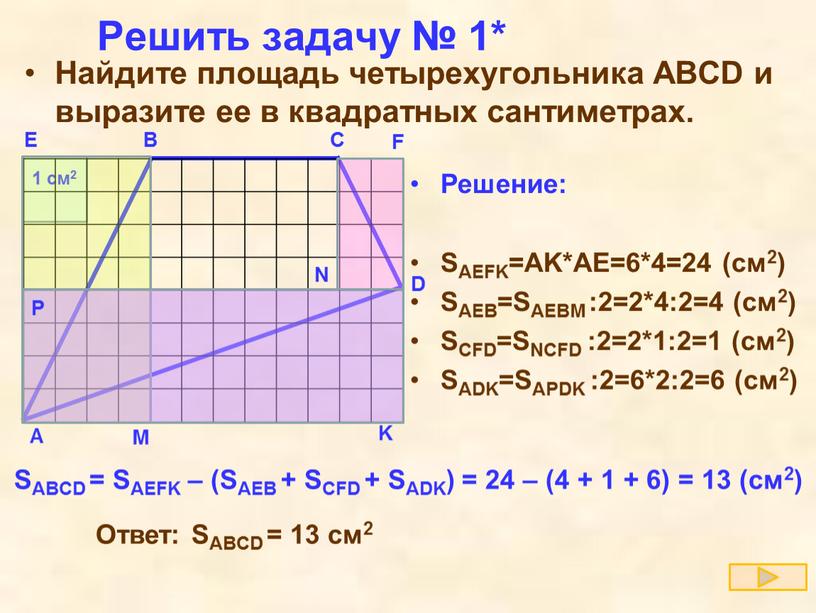
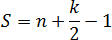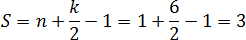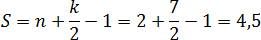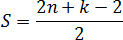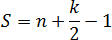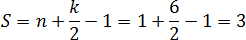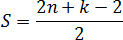что такое узлы координатной сетки
Задача B5: метод узлов
Сегодня мы научимся считать площади фигур в задаче B5 методом узлов. Для начала введем два определения:
Давайте посмотрим, как эти узлы выглядят на конкретной фигуре в задаче B5 из ЕГЭ по математике:
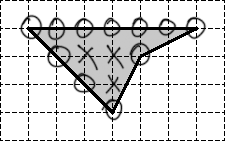
Задача. Найдите площадь четырехугольника изображенного на клетчатой бумаге с размером клетки 1 см × 1 см. Ответ дайте в квадратных сантиметрах.
Крестиками обозначены внутренние узлы. Очевидно, их количество n = 3. Кружками обозначены граничные узлы. Их общее количество равно k = 11.
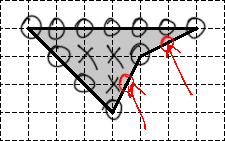
Обратите внимание: под узлами подразумеваются только те точки, которые лежат на пересечении горизонтальных и вертикальных линий нашей сетки. Другими словами, следующие две точки не являются узлами, хотя в них граница фигуры также пересекается с линиями сетки:
Переходим к решению задачи. Для того, чтобы решать задачи B5 ЕГЭ по математике методом узлов, вам потребуется запомнить следующую теорему:
Пусть дана фигура с n внутренними узлами и k граничными узлами. Тогда площадь этой фигуры S считается по формуле:
Вот так все просто! Главное — запомните, что n — это число внутренних узлов, а k — число граничных узлов.
В нашем случае мы уже подсчитали, что n = 3, k = 11. Подставляем полученные числа в формулу и получаем:
S = 3 + 0,5 · 11 − 1 = 3 + 5,5 − 1 = 7,5
Вот и все решение! Мы получили ответ: площадь четырехугольника равна 7,5. Как видите, задача свелась практически к устному счету. Поэтому обязательно возьмите данный прием на вооружение, ведь велика вероятность того, что на настоящем ЕГЭ по математике вам попадется именно такая задача B5 — площадь фигур на координатной сетке.
Метод узлов в задаче B5
Существует замечательная формула, которая позволяет считать площадь многоугольника на координатной сетке почти без ошибок. Это даже не формула, а настоящая теорема. На первый взгляд, она может показаться сложной. Но достаточно решить пару задач — и вы поймете, насколько это крутая фишка. Так что вперед!
Для начала введем новое определение:
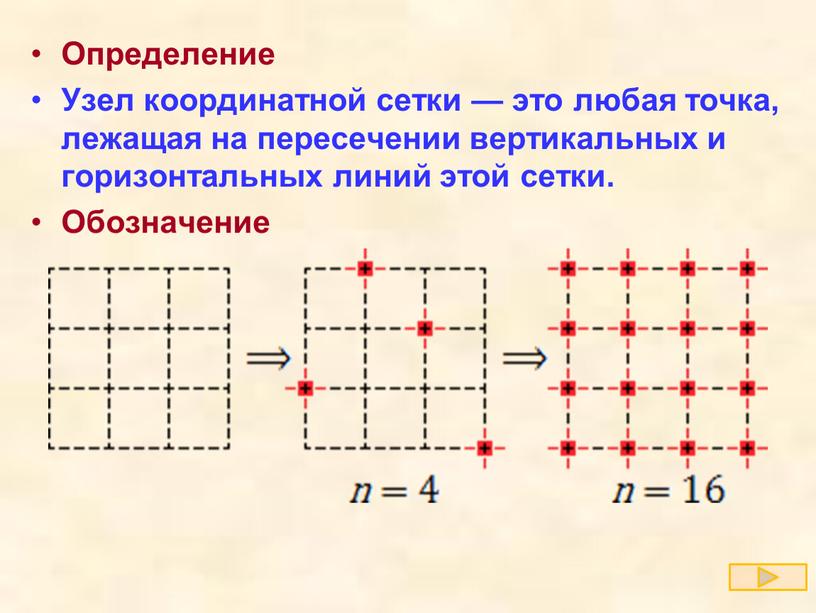
— это любая точка, лежащая на пересечении вертикальных и горизонтальных линий этой сетки.
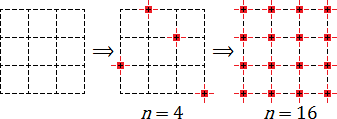
На первой картинке узлы вообще не обозначены. На второй обозначены 4 узла. Наконец, на третьей картинке обозначены все 16 узлов.
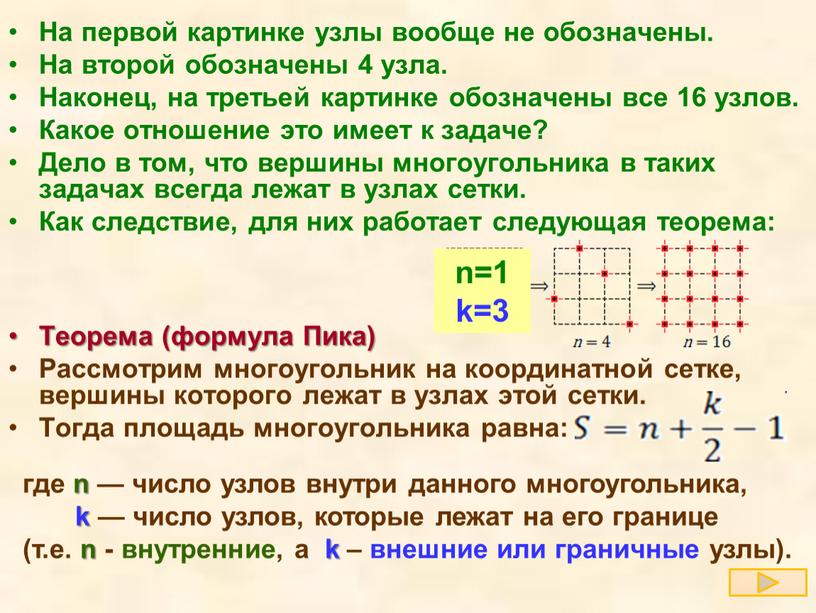
Какое отношение это имеет к задаче B5? Дело в том, что вершины многоугольника в таких задачах всегда лежат в узлах сетки. Как следствие, для них работает следующая теорема:
Теорема. Рассмотрим многоугольник на координатной сетке, вершины которого лежат в узлах этой сетки. Тогда площадь многоугольника равна:
где n — число узлов внутри данного многоугольника, число узлов, которые лежат на его границе (граничных узлов).
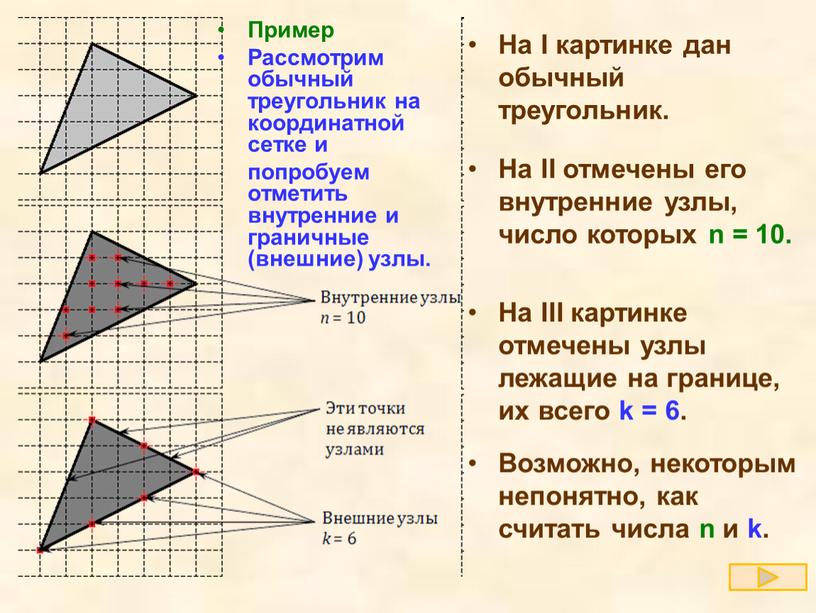
В качестве примера рассмотрим обычный треугольник на координатной сетке и попробуем отметить внутренние и граничные узлы.
На первой картинке дан обычный треугольник. На второй отмечены его внутренние узлы, число которых равно На третей картинке отмечены узлы лежащие на границе, их всего
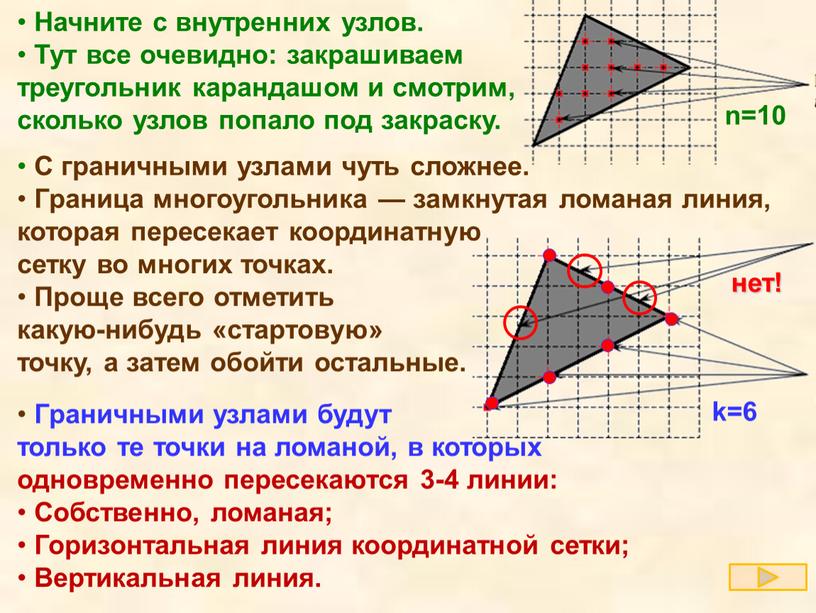
Возможно, многим читателям непонятно, как считать числа Начните с внутренних узлов. Тут все очевидно: закрашиваем треугольник карандашом и смотрим, сколько узлов попало под закраску.
С граничными узлами чуть сложнее. Граница многоугольника — замкнутая ломаная, которая пересекает координатную сетку во многих точках. Проще всего отметить какую-нибудь «стартовую» точку, а затем обойти остальные.
Граничными узлами будут только те точки на ломаной, в которых одновременно пересекаются
Посмотрим, как все это работает в настоящих задачах.
Задача. Найдите площадь треугольника, если размер клетки равен 1 x 1 см:
Для начала отметим узлы, которые лежат внутри треугольника, а также на его границе:
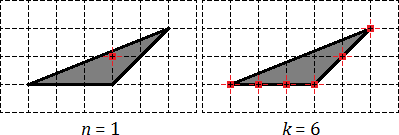
Получается, что внутренний узел всего один: Граничных узлов — целых шесть: три совпадают с вершинами треугольника, а еще три лежат на сторонах.
Теперь считаем площадь по формуле:
Вот и все! Задача решена.
Задача. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см на 1 см. Ответ дайте в квадратных сантиметрах.
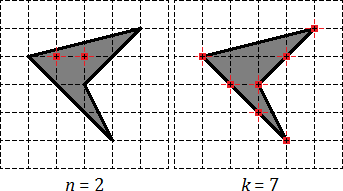
Снова отмечаем внутренние и граничные узлы. Внутренних узлов всего Граничных узлов: из которых 4 являются вершинами четырехугольника, а еще 3 лежат на сторонах.
Остается подставить числа в формулу площади:
Обратите внимание на последний пример. Эту задачу реально предлагали на диагностической работе в 2012 году. Если работать по стандартной схеме, придется делать много дополнительных построений. А методом узлов все решается практически устно.
Важное замечание по площадям
Но формула — это еще не все. Давайте немного перепишем формулу, приведя слагаемые в правой части к общему знаменателю. Получим:
Числа n и k — это количество узлов, они всегда целые. Значит, весь числитель тоже целый. Мы делим его на 2, из чего следует важный факт:
Площадь всегда выражается целым числом или дробью. Причем в конце дроби всегда стоит «пять десятых»: 10,5; 17,5 и т.д.
Таким образом, площадь в задаче B5 всегда выражается целым числом или дробью Если ответ получается другим, значит, где-то допущена ошибка. Помните об этом, когда будете сдавать настоящий ЕГЭ по математике!
Метод узлов
Существует замечательная формула, которая позволяет считать площадь многоугольника на координатной сетке почти без ошибок. Это даже не формула, а настоящая теорема. На первый взгляд, она может показаться сложной. Но достаточно решить пару задач — и вы поймете, насколько это крутая фишка. Так что вперед!
Для начала введем новое определение:
— это любая точка, лежащая на пересечении вертикальных и горизонтальных линий этой сетки.
Обозначение
На первой картинке узлы вообще не обозначены. На второй обозначены 4 узла. Наконец, на третьей картинке обозначены все 16 узлов.
Какое отношение это имеет к задаче B5? Дело в том, что вершины многоугольника в таких задачах всегда лежат в узлах сетки. Как следствие, для них работает следующая теорема:
Теорема
Рассмотрим многоугольник на координатной сетке, вершины которого лежат в узлах этой сетки. Тогда площадь многоугольника равна:
где n — число узлов внутри данного многоугольника, число узлов, которые лежат на его границе (граничных узлов).
Задача:
Рассмотрим обычный треугольник на координатной сетке и попробуем отметить внутренние и граничные узлы.
На первой картинке дан обычный треугольник. На второй отмечены его внутренние узлы, число которых равно На третей картинке отмечены узлы лежащие на границе, их всего
Возможно, многим читателям непонятно, как считать числа Начните с внутренних узлов. Тут все очевидно: закрашиваем треугольник карандашом и смотрим, сколько узлов попало под закраску.
С граничными узлами чуть сложнее. Граница многоугольника — замкнутая ломаная, которая пересекает координатную сетку во многих точках. Проще всего отметить какую-нибудь «стартовую» точку, а затем обойти остальные.
Граничными узлами будут только те точки на ломаной, в которых одновременно пересекаются
Посмотрим, как все это работает в настоящих задачах.
Задача 2:
Найдите площадь треугольника, если размер клетки равен 1 x 1 см:
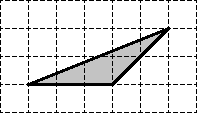
Для начала отметим узлы, которые лежат внутри треугольника, а также на его границе:
Получается, что внутренний узел всего один: Граничных узлов — целых шесть: три совпадают с вершинами треугольника, а еще три лежат на сторонах.
Теперь считаем площадь по формуле:
Вот и все! Задача решена.
Задача 3:
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см на 1 см. Ответ дайте в квадратных сантиметрах.

Снова отмечаем внутренние и граничные узлы. Внутренних узлов всего Граничных узлов: из которых 4 являются вершинами четырехугольника, а еще 3 лежат на сторонах.
Остается подставить числа в формулу площади:
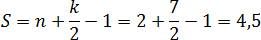
Обратите внимание на последний пример. Эту задачу реально предлагали на диагностической работе в 2012 году. Если работать по стандартной схеме, придется делать много дополнительных построений. А методом узлов все решается практически устно.
Важное замечание по площадям
Но формула — это еще не все. Давайте немного перепишем формулу, приведя слагаемые в правой части к общему знаменателю. Получим:
Числа n и k — это количество узлов, они всегда целые. Значит, весь числитель тоже целый. Мы делим его на 2, из чего следует важный факт:
Площадь всегда выражается целым числом или дробью. Причем в конце дроби всегда стоит «пять десятых»:
Таким образом, площадь в задаче B5 всегда выражается целым числом или дробью Если ответ получается другим, значит, где-то допущена ошибка. Помните об этом, когда будете сдавать настоящий ЕГЭ по математике!
Сегодня мы научились считать площади фигур в задаче B5 методом узлов. Повторим, что для начала введят два определения:
Давайте посмотрим, как эти узлы выглядят на конкретной фигуре в задаче B5
Задача. Найдите площадь четырехугольника изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.
Крестиками обозначены внутренние узлы. Очевидно, их количество Кружками обозначены граничные узлы. Их общее количество равно
Обратите внимание: под узлами подразумеваются только те точки, которые лежат на пересечении горизонтальных и вертикальных линий нашей сетки. Другими словами, следующие две точки не являются узлами, хотя в них граница фигуры также пересекается с линиями сетки:
Переходим к решению задачи. Для того, чтобы решать задачи B5 ЕГЭ по математике методом узлов, вам потребуется запомнить следующую теорему:
Теорема. Пусть дана фигура с внутренними узлами и граничными узлами. Тогда площадь этой фигуры считается по формуле:
S = n + 0,5 k − 1
Вот так все просто! Главное — запомните, это число внутренних узлов, число граничных узлов.
В нашем случае мы уже подсчитали, что Подставляем полученные числа в формулу и получаем:
Мы получили ответ: площадь четырехугольника
Ответ: 7,5
Как видите, задача свелась практически к устному счету. Поэтому обязательно возьмите данный прием на вооружение, ведь велика вероятность того, что на настоящем ЕГЭ по математике вам попадется именно такая задача B5 — площадь фигур на координатной сетке.
КДМ. Площадь многоугольника: разбиение фигуры на части и «метод узлов» по формуле Пика.
Площадь фигуры (многоугольника)
Площадь фигуры (многоугольника)
В задании требуется всегда одно и то же: найти площадь фигуры, которая задана точками на координатной плоскости или на координатной сетке
В задании требуется всегда одно и то же: найти площадь фигуры, которая задана точками на координатной плоскости или на координатной сетке.
В зависимости от фигуры, все задачи делятся на два типа:
Площадь многоугольника;
Площадь круга.
Независимо от типа, надо помнить важнейшее правило, вытекающее из свойств площади: если фигуру разрезать на несколько частей, то сумма площадей этих частей равна площади всей фигуры.
Рассмотрим площадь многоугольника.
Решить задачу № 1* Найдите площадь четырехугольника
Найдите площадь четырехугольника ABCD и выразите ее в квадратных сантиметрах.
Найдите площадь в см2
прямоугольника AEFK
Найдите площадь в см2
прямоугольных
треугольников AEB, CFD,
ADK
Найдите площадь четырехугольника ABCD
Решить задачу № 1* Найдите площадь четырехугольника
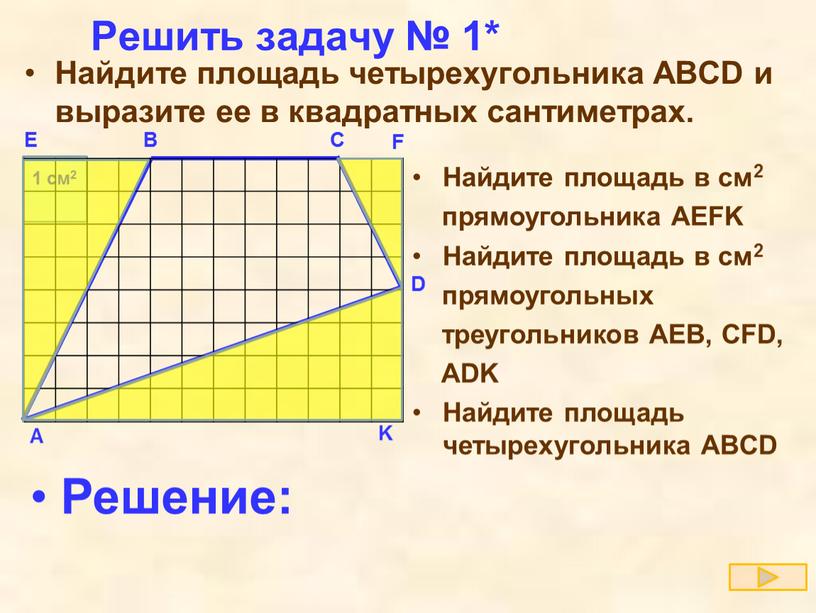
Найдите площадь четырехугольника ABCD и выразите ее в квадратных сантиметрах.
Найдите площадь
прямоугольника AEFK в см2
Найдите площадь прямоугольных треугольников AEB, CFD, ADK в см2
Найдите площадь четырехугольника ABCD
Решить задачу № 1* Найдите площадь четырехугольника
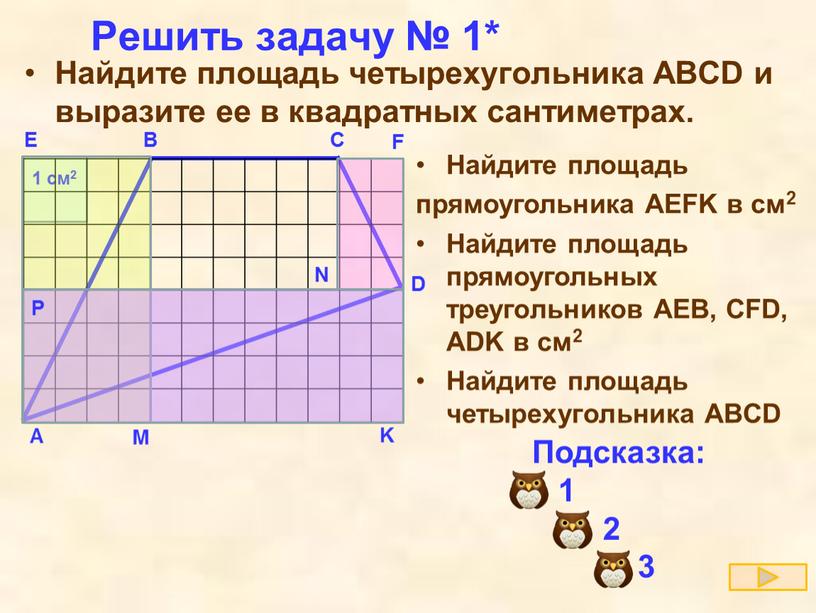
Найдите площадь четырехугольника ABCD и выразите ее в квадратных сантиметрах.
SAEFK=AK*AE=6*4=24 (см2)
SAEB=SAEBM :2=2*4:2=4 (см2)
SCFD=SNCFD :2=2*1:2=1 (см2)
SADK=SAPDK :2=6*2:2=6 (см2)
SABCD = SAEFK – (SAEB + SCFD + SADK) = 24 – (4 + 1 + 6) = 13 (см2)
Ответ: SABCD = 13 см2
Эту формулу редко кто изучает в школе…
Эту формулу редко кто изучает в школе…
О ней, вряд ли, вспомнят в колледже или даже в университете.
Но те, кто ее знают, всегда решат задачу правильно.
Никаких дополнительных построений и треугольников — все намного проще.
Запоминайте и пользуйтесь
замечательной формулой!
Метод узлов
А я знаю, как решить такую задачу намного проще и быстрее!
Есть отличная формула.
Существует замечательная формула, которая позволяет считать площадь многоугольника на координатной сетке почти без ошибок
Существует замечательная формула, которая позволяет считать площадь многоугольника на координатной сетке почти без ошибок.
Это даже не формула, а настоящая теорема.
На первый взгляд, она может показаться сложной.
Но достаточно решить пару задач — и вы поймете, насколько это крутая фишка.
Так что вперед!
Для начала введем новое определение:
Определение Узел координатной сетки — это любая точка, лежащая на пересечении вертикальных и горизонтальных линий этой сетки
Определение
Узел координатной сетки — это любая точка, лежащая на пересечении вертикальных и горизонтальных линий этой сетки.
Обозначение
На первой картинке узлы вообще не обозначены
На первой картинке узлы вообще не обозначены.
На второй обозначены 4 узла.
Наконец, на третьей картинке обозначены все 16 узлов.
Какое отношение это имеет к задаче?
Дело в том, что вершины многоугольника в таких задачах всегда лежат в узлах сетки.
Как следствие, для них работает следующая теорема:
Теорема (формула Пика)
Рассмотрим многоугольник на координатной сетке, вершины которого лежат в узлах этой сетки.
Тогда площадь многоугольника равна:
Пример Рассмотрим обычный треугольник на координатной сетке и попробуем отметить внутренние и граничные (внешние) узлы
Пример
Рассмотрим обычный треугольник на координатной сетке и
попробуем отметить внутренние и граничные (внешние) узлы.
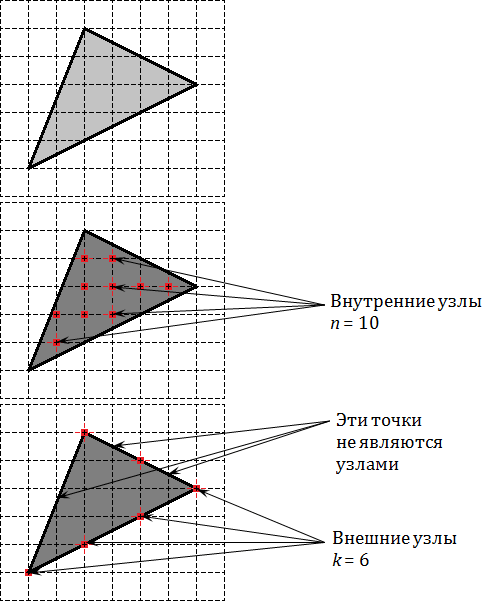
На I картинке дан обычный треугольник.
На II отмечены его внутренние узлы, число которых n = 10.
На III картинке отмечены узлы лежащие на границе, их всего k = 6.
Возможно, некоторым непонятно, как считать числа n и k.
Начните с внутренних узлов. Тут все очевидно: закрашиваем треугольник карандашом и смотрим, сколько узлов попало под закраску
Начните с внутренних узлов.
Тут все очевидно: закрашиваем
треугольник карандашом и смотрим,
сколько узлов попало под закраску.
С граничными узлами чуть сложнее.
Граница многоугольника — замкнутая ломаная линия, которая пересекает координатную
сетку во многих точках.
Проще всего отметить
какую-нибудь «стартовую»
точку, а затем обойти остальные.
Граничными узлами будут
только те точки на ломаной, в которых
одновременно пересекаются 3-4 линии:
Собственно, ломаная;
Горизонтальная линия координатной сетки;
Вертикальная линия.
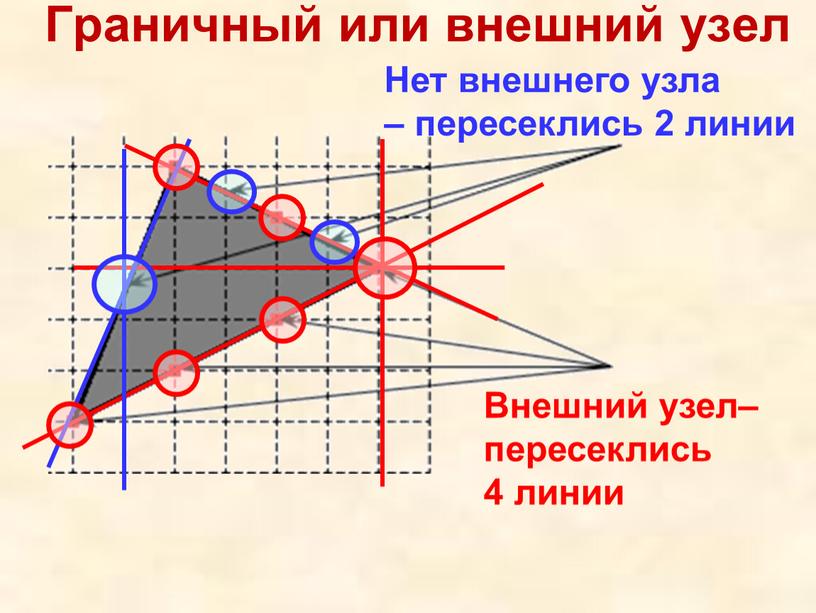
Граничный или внешний узел Нет внешнего узла – пересеклись 2 линии
Граничный или внешний узел
Нет внешнего узла
– пересеклись 2 линии
Внешний узел–
пересеклись
4 линии
Формула Пика В 1899 г. австрийский математик
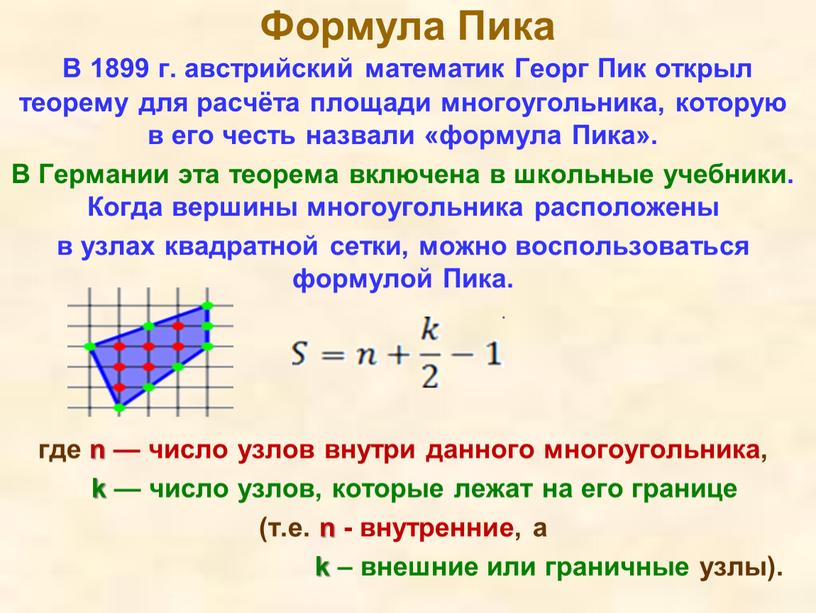
В 1899 г. австрийский математик Георг Пик открыл теорему для расчёта площади многоугольника, которую в его честь назвали «формула Пика».
В Германии эта теорема включена в школьные учебники. Когда вершины многоугольника расположены
в узлах квадратной сетки, можно воспользоваться формулой Пика.
Георг Алекса́ндр Пик (нем. Georg
Что такое узлы координатной сетки
ГОСУДАРСТВЕННЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Шаги координатной сетки
Printed boards. Grid systems
Дата введения 1998-01-01
1 РАЗРАБОТАН АООТ Центральным научно-исследовательским институтом «Техномаш»
ВНЕСЕН Всероссийским научно-исследовательским институтом «Эталон»
2 ПРИНЯТ И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Госстандарта России от 26 марта 1997 г. N 104
3 Стандарт соответствует Международному стандарту МЭК 97-91 в части применения координатной сетки для печатных плат
1 ОБЛАСТЬ ПРИМЕНЕНИЯ
Настоящий стандарт распространяется на печатные платы независимо от вида, конструктивных особенностей и метода изготовления.
2 НОРМАТИВНЫЕ ССЫЛКИ
В настоящем стандарте использована ссылка на
ГОСТ 20406-75 Платы печатные. Термины и определения
3 ОПРЕДЕЛЕНИЯ
В настоящем стандарте применяют термины по ГОСТ 20406, а также следующие термины:
4 ОСНОВНЫЕ ШАГИ КООРДИНАТНОЙ СЕТКИ
4.1 Для размещения соединений на печатной плате должна применяться координатная сетка с номинальным шагом 0,50 мм в обоих направлениях.
4.2 Если координатная сетка с номинальным шагом 0,50 мм не удовлетворяет требованиям конкретной конструкции, то должна применяться координатная сетка с номинальным шагом 0,05 мм.
4.3 Для конкретных конструкций, использующих элементную базу с шагом 0,625 мм, допускается применение шага координатной сетки 0,625 мм.
5 ПРЕДПОЧТИТЕЛЬНЫЙ ШАГ КООРДИНАТНОЙ СЕТКИ
5.1 При необходимости применения координатной сетки с шагом, отличным от основных, шаг ее должен быть кратным основным шагам координатной сетки.
5.2 Предпочтительные модули для координатных сеток с шагом 0,50; 0,05 мм и соответствующие им значения кратных шагов координатной сетки приведены в таблице 1.
Основной шаг координатной сетки
Предпочтительный шаг координатной сетки