что такое утверждение в логике
логическое утверждение
Смотреть что такое «логическое утверждение» в других словарях:
Логическое высказывание — утверждение, которому всегда можно поставить в соответствие одно из двух логических значений: ложь (0, ложно, false) или истина (1, истинно, true). Логическое высказывание принято обозначать заглавными латинскими буквами. Высказывательной формой… … Википедия
ЛОГИЧЕСКОЕ И ИСТОРИЧЕСКОЕ — см. Историческое и логическое. Философский энциклопедический словарь. М.: Советская энциклопедия. Гл. редакция: Л. Ф. Ильичёв, П. Н. Федосеев, С. М. Ковалёв, В. Г. Панов. 1983. ЛОГИЧЕСКОЕ И ИСТОРИЧЕСКОЕ … Философская энциклопедия
ЛОГИЧЕСКОЕ СЛЕДОВАНИЕ — отношение между некоторыми высказываниями (посылками) Г и высказыванием В (заключением), отображающее тот факт, что из Г, используя правильные приёмы рассуждения, можно получить В. В логике, фиксирующей нормы рассуждения с помощью… … Философская энциклопедия
Логическое мышление — Логика (др. греч. λογική «наука о рассуждении», «искусство рассуждения» от λόγος «речь», «рассуждение») наука о формах, методах и законах интеллектуальной познавательной деятельности, формализуемых с помощью логического языка. Поскольку это… … Википедия
Логическое «или» — Дизъюнкция логическая операция, по своему применению максимально приближенная к союзу «или» в смысле «или то, или это, или оба сразу». Синонимы: логическое «ИЛИ», включающее «ИЛИ», логическое сложение, иногда просто «ИЛИ». Это бинарная инфиксная … Википедия
Логическое ИЛИ — Дизъюнкция логическая операция, по своему применению максимально приближенная к союзу «или» в смысле «или то, или это, или оба сразу». Синонимы: логическое «ИЛИ», включающее «ИЛИ», логическое сложение, иногда просто «ИЛИ». Это бинарная инфиксная … Википедия
Логическое сложение — Дизъюнкция логическая операция, по своему применению максимально приближенная к союзу «или» в смысле «или то, или это, или оба сразу». Синонимы: логическое «ИЛИ», включающее «ИЛИ», логическое сложение, иногда просто «ИЛИ». Это бинарная инфиксная … Википедия
Логическое отрицание — Отрицание в логике унарная операция над суждениями, результатом которой является суждение (в известном смысле) «противоположное» исходному. Обозначается знаком ¬ Как в классической, так и в интуиционистской логике «двойное отрицание» ¬¬A является … Википедия
ПРОТИВОРЕЧИЕ ЛОГИЧЕСКОЕ — ПРОТИВОРЕЧИЕ ЛОГИЧЕСКОЕ утверждение одновременного наличия некоторой ситуации А и отсутствия этой ситуации. В языке выражается утверждением А и не А: (Α& Α), которое является тождественно ложным. Методологическое значение логических… … Философская энциклопедия
СЛЕДОВАНИЕ ЛОГИЧЕСКОЕ — СЛЕДОВАНИЕ ЛОГИЧЕСКОЕ отношение между некоторым множеством высказываний Г (гипотез) и высказыванием В (заключением), отображающее тот факт, что, в силу только логической структуры названных высказываний и, значит, независимо от их содержания… … Философская энциклопедия
9. Краткий курс классической логики. Суждение
Суждение – это форма мышления, в которой что-либо утверждается или отрицается. Примеры суждений: «Некоторые студенты – отличники», «Все люди – смертные».
Суждения составляется из понятий, оно предоставляет собой чаще всего повествовательное предложение. В редких случаях оно бывает риторическое-восклицательное или риторическое-вопросительное предложение, которое что-то утверждает или отрицает.
Бывают простые и сложные суждения, сложные суждения складываются из двух или более простых суждений соединённых союзом.
Суждение на отмену от понятий бывают истинные и ложные, а так же имеют сложную структуру, которая складывается из таких понятий:
Субъект и предикат суждения могут состоять в отношениях:
1.Равнозначности – когда объем субъекта равен объёму предиката. «Все квадраты – равносторонние прямоугольники».
2.Подчинения – когда объем субъекта входит в объем предиката или наоборот. «Все березы – это деревья». Объем понятия деревья больше понятия березы, так как береза только одно из разновидностей деревьев.
3.Пересечения – когда объемы субъекта и предиката пересекаются частично, к примеру, «Некоторые литераторы – это лауреаты нобелевской премии». Литераторы могут быть лауреатами нобелевской премии, но могут и не быть, так же как и лауреаты нобелевской премии могут быть литераторами, но могут ими и не быть. Объем этих понятий совпадает только в некоторых случаях, потому субъект и предикат находятся в отношении пересечения.
4.Несовместимости – когда объемы субъекта и предиката не имеют общих точек соприкосновения. «Звезды – это не планеты». Чаще субъект и предикат, входя в третье более общее понятия, в нашем случае – это небесные тела.
Важно заметить, что при обращении, суждения меняют свой тип, согласно ниже приведенных примеров:
Суждения типа А:
равнозначности – обращается в самое себя.
подчинения – обращается в суждения типа I.
Суждения типа I:
пересечения – обращается в самое себя.
подчинения – обращается в суждения типа I.
Суждения типа Е:
несовместимости – обращается в самое себя.
Суждения типа О:
пересечения – обращению не поддается.
подчинения – обращению не поддаётся.
Второе действие над суждениями — превращения. Оно заключается в том, что у суждения меняется связка, положительная на отрицательную или наоборот. При этом предикат суждения меняется на противоречащий, перед ним ставиться частица «не». Вернемся к нашему исходному суждению: «Все акулы – являются рыбами». Результатом превращения будет суждения: «Все акулы не являются не рыбами». Выглядит это суждения непривычно, однако это более короткое изречение той мысли, что если какое-то животное не являются акулой, то оно не являются и рыбой. Или, что если какое-то животное является акулой то оно обязательно должно являться рыбой, ни одна акула не может быть таким существом, которое бы не являлось при этом рыбой.
В отличие от обращения превращение не зависит от характера отношения субъекта и предиката простого суждения:
Суждения типа А всегда превращается в суждения типа Е, и наоборот.
Суждения типа I всегда превращается в суждения типа О, и наоборот.
При действии противоставления предикату суждения меняют свой тип, аналогично обращении.
В итоге, из одного суждения, мы можем получить четыре:
1. Исходное суждение: «Все акулы являются рыбами».
2. Результат обращения: «Некоторые рыбы – это акулы».
3. Результат превращения: «Все акулы не являются не рыбами».
4. Результат противоставления предикату: «Все не рыбы не являются акулами».
Если мы разобрались с этим, то совершить превращения и противоставления предикату этого суждения совсем не проблематично. Получиться, как и в первом варианте — четыре суждения:
Исходное суждение: «Идти назад – значит не идти вперед»
Обращения: «Иногда не идти вперед, значит идти назад».
Превращения: «Идти назад не означает, не идти вперед».
Противоставление предикату: «Иногда не идти вперед не означает, не идти назад».
Несовместимые суждения находятся в отношениях:
Противоположности (контарность) – суждения, в которых, так же как при отношении частичного совпадения, субъект и предикат совпадает, а связка отличается, но в этом случае суждения могут быть только общими: общеутвердительными (А) или общеотрицательными (О). «Все люди – лгут», «Все люди – не лгут». Важным признаком противоположных суждений является то, что они не могут быть одновременно истинные как несовместимые, но при этом могут быть одновременно ложными. Между этими суждениями всегда можно вставить третье, нейтральное утверждение. В нашем примере это «Некоторые люди лгут, а некоторые не лгут». Это суждение, будучи истинным, доказывает ложность двух первых.
Противоречия (контрадикторность) – это отношения между двумя суждениями в которых предикаты совпадают, связки отличаются, а субъекты находятся в родовом, видовом отношении, то есть отличаются объемами. «Все люди – являются разумными существами», Некоторые люди – не являются разумными существами». На отмену от противоположных суждений противоречивые, не могу быть одновременно ложными. Ложность одного непременно будет доказательством истинности другого, и наоборот.
Возможные отношения между простыми суждениями отображают посредством, так называемого логического квадрата:
Истинное значение суждения, связано с истинностью значений всех других сравнимых суждений. К примеру если суждения типа А: «Все акулы – являются рыбами» истинно, смотря на логический квадрат, можно определить, что суждения типа I: «Некоторые рыбы – являются акулами», тоже будет истинным. Суждения типа Е: «Все акулы – не являются рыбами», точно так же как и суждения типа О: «Некоторые акулы – не являются рыбами», будут ложными.
Еще несколько слов о сложных суждениях. В зависимости от союза, которым соединяются простые суждения в сложные, выделяют пять видов сложного суждения:
Утверждение (логика)
Оглавление
двусмысленность
Значение выражения, данного во введении, является преобладающим значением.
Однако термин « заявление» используется неоднозначно.
Их можно свести к четырем основным значениям:
Смысл выражения «утверждение» зависит от того, «что именно является объектом логики» и что на самом деле является «носителем» истины или лжи. Однако этот вопрос не нуждается в пояснении для технического использования логики.
Заявления и заявления
Согласно широко распространенному, но противоречивому мнению, утверждения не являются предложениями, а утверждения являются (только) лингвистическим выражением утверждений. Утверждение является репрезентативным для высказывания, является только знаком для высказывания (суждения) и только «лингвистическим коррелятом высказывания».
Возражение против приравнивания утверждения и предложения-утверждения состоит в том, что утверждение, «которое сделано с этим утверждением», должно отличаться от типа предложения и его высказывания.
Пример 2: Когда Ханс и Ина говорят «Я болен», то оба произносят одно и то же предложение (с точки зрения типа предложения), генерируют разные вхождения предложения и делают разные утверждения своими высказываниями.
Тугендхат примерно говорит о лингвистической, психологической и онтологической базовой концепции логики: лингвистическое высказывание соответствует суждению как психологическому акту и онтологически высказыванию, мысли (Фреге); факты (Гуссерль: Витгенштейн I ) или суждение (английская философия).
Разграничения
требовать
Ценностное суждение
Форма заявления
слово
За каждым термином стоит одно или несколько утверждений, которые определяют его содержание и связывают этот термин с другими. «Следовательно, утверждение о том, что понятие является единицей характеристик по своему содержанию, приводит к идее, что каждое понятие представляет собой связь высказываний». Это особенно поддерживалось Коном, а также поддержано Фреге, когда он сказал, что слово имеет только значение в предложении.
Достаточно
«Каждое утверждение, в котором что-то приписывается объекту, можно рассматривать как своего рода вывод, предпосылки которого определяют предмет рассматриваемого утверждения и приписывают или отрицают свойство термину, который его определяет».
Типы заявлений
З. Например, разделение утверждения «Дорога мокрая и идет дождь» на два утверждения, которые связаны между собой и образуют утверждение, больше не является таким разделением для отдельных утверждений «Дорога мокрая» и «Идет дождь». возможный. Таким образом, эти операторы являются атомарными операторами. При пропозициональном анализе аргументов важно подразделить формулировки на атомарные утверждения, поскольку это единственный способ формализовать соединения, которые важны для структуры аргумента.
В простом заявлении объекту присваивается или запрещается единственный предикат.
Когда говорится, что простой оператор не имеет дополнительной структуры, следует понимать, что внутренняя структура оператора не уточняется.
Интерпретация атомарных предложений осуществляется путем присвоения значений истинности.
Эти символы для простых утверждений являются предметом конвенции. Обычно используется, например, использование заглавных букв A, B, C, возможно, с индексированными буквами.
Связь утверждений может быть расширенной (экстенсиональная связь утверждений) или интенсиональной (размерная связь утверждений).
Есть шестнадцать двузначных ссылок (переходов) для объединения двух утверждений. Для всех возможных комбинаций значений истинности вы указываете типичное значение истинности результата для этой ссылки. Например, конъюнктно связанный оператор a AND b истинен только в том случае, если истинны и a, и b; в любом другом случае соединение неверно.
Пример: «Антон читает книгу о логике, потому что считает логику невероятно увлекательной».
Высказывания традиционно делятся на аналитические утверждения и синтетические утверждения. Вместо «утверждения», «предложение» или «суждение» также используется в том же смысле (см. Выше трехстороннее деление Тугендхат).
Утверждения логики высказываний
Утверждения в логике предикатов
Урок 4. Суждения и высказывания. Введение в силлогистику
В прошлых уроках рассказывалось о том, как правильно работать с понятиями и определениями. Хотя операции над ними очень важны и встречаются повсеместно, сами по себе они ещё не составляют рассуждений. В этом уроке мы как раз приблизимся к теме того, как правильно рассуждать. Мы будем рассматривать рассуждения на примере силлогистики. Силлогистика – это самая древняя логическая система. Она была изобретена древнегреческим философом Аристотелем в IVвеке до н.э. До сих пор она остаётся одной из самых понятных, приближенных к естественному языку и лёгких для изучения логических систем. Одно из главных её достоинств – возможность применения в повседневных ситуациях без особых усилий.
Содержание:
Суждения и высказывания
Что такое рассуждение? Можно было бы сказать: вывод, умозаключение, размышление, доказательство и т.д. Всё это верно, но, пожалуй, самым очевидным ответом было бы: рассуждение – это последовательность суждений, которые в идеале должны быть связаны между собой согласно правилам логики. Поэтому обучение правильному рассуждению нужно начинать с того, что такое суждения и как ими корректно пользоваться.
Суждение – это мысль об утверждении или отрицании наличия некоторой ситуации в мире.
В естественном языке суждения передаются с помощью повествовательных предложений, или высказываний. Примеры суждений, выраженных в высказываниях: «Пришла осень», «Катя не знает английского языка», «Я люблю читать», «Трава зелёная, а небо голубое». Одно и то же суждение может быть выражено с помощь разных высказываний, в частности: «Небо голубое» и «The sky is blue» – разные высказывания, но суждение они выражают одно и то же, так как они передают одну и ту же мысль. Точно также высказывания «Никто не покидал дома» и «Все оставались дома» разные, но они передают одно суждение.
Поскольку высказывания посредством суждений фиксируют какое-то положение дел в мире, в отличие от понятий и определений, мы можем оценивать их с точки зрения их истинности и ложности. Так высказывание «Бил Гейтс основал компанию “Microsoft”» – истинное, а высказывание «Апельсины фиолетовые» – ложное.
Если вспомнить треугольник Фреге, то высказывание будет находиться на вершине, обозначающей знак, суждение будет составлять его смысл, а истина и ложь – значение.
Существует множество типов суждений и, соответственно, высказываний. Разные логические системы концентрируются на их разных аспектах. Силлогистика работает с так называемыми категорическими атрибутивными высказываниями. Категорические высказывания противопоставляются гипотетическим. Гипотетические высказывания говорят о возможности наличия или отсутствия какой-то ситуации в мире: «Возможно, пойдёт дождь». Категорические высказывания безапелляционно утверждают о том, что какая-то ситуация имеется или не имеется: «Пошёл дождь». Термин «атрибутивный» означает, что эти высказывания говорят о наличии либо отсутствии у предмета или класса предметов некоторого свойства. Примеры категорических атрибутивных высказываний: «Моя машина синего цвета», «Парк около нашего дома большой», «Никто не любит рыбий жир», «Некоторые люди считают, что они самые умные». Хотя на первый взгляд может показаться, что из-за концентрации именно на категорических атрибутивных высказываниях, применение силлогистики ограничено, это не так. Огромный пласт рассуждений не выходит за рамки подобных высказываний, а потому знания силлогистики оказывается достаточно для того, чтобы научиться размышлять логично и не давать ввести себя в заблуждение.
Состав и виды категорических атрибутивных высказываний
Категорические атрибутивные высказывания состоят из терминов, предицирующих связок и кванторов.
Термины делятся на субъект и предикат.
Предицирующие связки, как, возможно, вы помните из первого урока, это связки «есть» и «не есть». В естественном языке они могут выражаться с помощью разных слов и конструкций: «есть», «являться», «суть», «это», «выступать», знака тире, глаголов, либо вообще опускаться.
Кванторы – это слова, указывающие на количественные характеристики субъекта. Существует два вида кванторов: квантор общности («все», «каждый», «любой», «ни один», «никто») и квантор существования («некоторые», «не все», «какой-либо», «многие»). Также как и предицирующие связки, кванторы в естественной речи могут опускаться. Мы можем сказать: «Люди равны перед законом», подразумевая, что «Все люди равны перед законом»; или «Дети любят сладкое» – подразумевая, что «Многие дети любят сладкое». Зачастую лучше всего уточнить у вашего собеседника, какой именно квантор он имеет в виду, так как это будет сказываться на условиях истинности его высказываний.
Давайте разберём следующее высказывание: «Кошки мурлычут, когда им приятно». «Кошки» – это субъект, «существа, мурлычущие, когда им приятно» – это предикат. Также здесь присутствует невидимая связка «есть», которая соединяет субъект с предикатом, и невидимый квантор общности «все». Так, если записать это высказывание в соответствии с его логической формой, то получим: «Все кошки есть существа, которые мурлычут, когда им приятно». Благодаря этому примеру становится ясно, что прежде чем определять, истинно высказывание или ложно, нужно выявить его логическую форму и преобразовать исходное высказывание так, чтобы все четыре элемента (квантор, субъект, связка, предикат) были на своих местах.
В зависимости от свойств логических и нелогических терминов, входящих в состав категорических атрибутивных высказываний, их можно разделить на несколько видов.
Если мы скомбинируем эти виды между собой, то получается, что всего существует шесть видов категорических атрибутивных высказываний:
Условия истинности для категорических атрибутивных высказываний в традиционной силлогистике
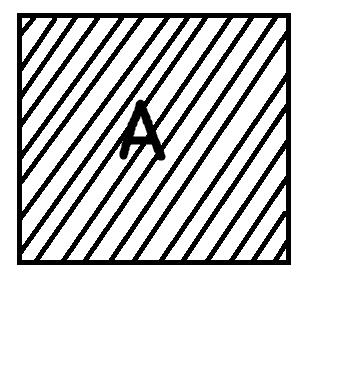
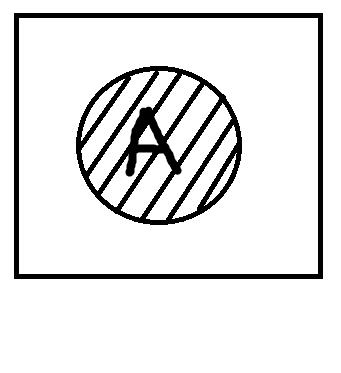
Следует начать с того, что традиционная силлогистика накладывает два ограничения на используемые термины, а именно: они должны быть непусты и неуниверсальны, то есть если под термин не подпадает ни один объект из универсума рассмотрения или, наоборот, подпадают все объекты универсума, то они не могут быть предметом рассмотрения. Посмотрим на рисунки:
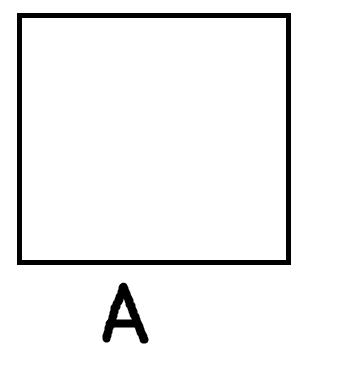
Первый рисунок изображает ситуацию, когда термин А пуст, поэтому весь квадратик (универсум рассмотрения) остался белым. Второй рисунок показывает случай, когда объём термина А совпадает с объёмом универсума рассмотрения, поэтому весь квадрат заштрихован. Последний рисунок репрезентирует термин А, который является непустым и в то же время неуниверсальным. Заштрихованая область соотвествует объёму А. Традиционная силлогистика работает только с терминами, которые соотвествуют третьему рисунку. Такое условие ставится для того, чтобы исключить из рассмотрения высказывания, которые невозможно оценить как истинные либо ложные. Возьмём высказывание: «Все дети Ивана лысые». Вроде бы с высказыванием всё впорядке, однако представьте, что у Ивана нет детей. Мы не можем в данном случае просто сказать, что высказывание ложное. Если назвать его ложным, то тем самым мы подразумеваем, что не все дети Ивана лысые, а это не так. В то же время мы не можем сказать, что оно истинное. Выход из этого затруднительного положения состоит как раз в том, чтобы указать на пустоту термина «дети Ивана». Поскольку у Ивана нет детей, этот термин пуст, и мы не можем построить с ним корректное высказывание.
Непустота и неуниверсальность термина будут определяться не только контекстом, но и выбранным универсумом рассмотрения. Если наш квадратик представляет собой универсум живых существ или материально существующих предметов, то, конечно, такие термины как «русалка», «хоббит», «дракон» и т.п. окажутся пустыми, и мы не сможем их рассматривать. Однако, если универсум рассмотрения – это мифологические или сказочные существа, то все эти термины перестают быть пустыми. То же самое верно и для универсальности. Термин «люди» может рассматриваться как универсальный, что исключает его из области традиционной силлогистики. Однако если мы хотим сказать «Сократ – человек», то в качестве универсума рассмотрения вполне можно взять живых существ. На универсуме живых существ, термин «люди» уже не будет универсальным.
Кроме того, нужно помнить, что субъект и предикат должны задаваться на одном и том же универсуме рассмотрения.
Теперь посмотрим, при каких условиях разные типы категориальных атрибутивных высказываний будут истинными. Для этого советуем ещё раз заглянуть в урок, посвящённый отношениям между понятиями. По большому счёту, субъект и предикат – это термины, представляющие некоторые понятия. Соответственно, если соединить эти понятия в одном предложении с помощью предицирующих связок и кванторов, то, чтобы узнать будут эти предложения истинными или ложными, достаточно посмотреть на диаграммы, иллюстрирующие отношения между этими двумя понятиями. Итак, преступим.
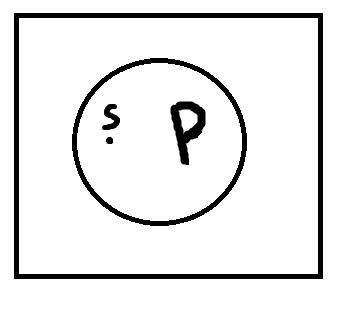
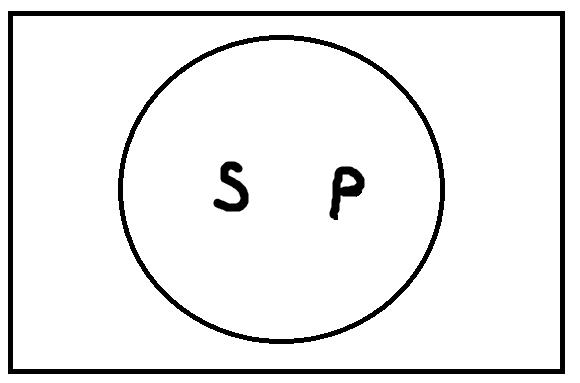
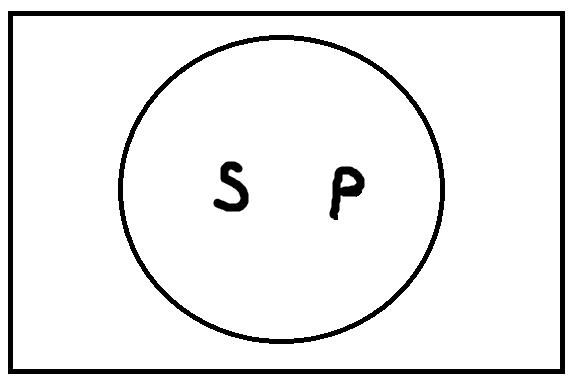
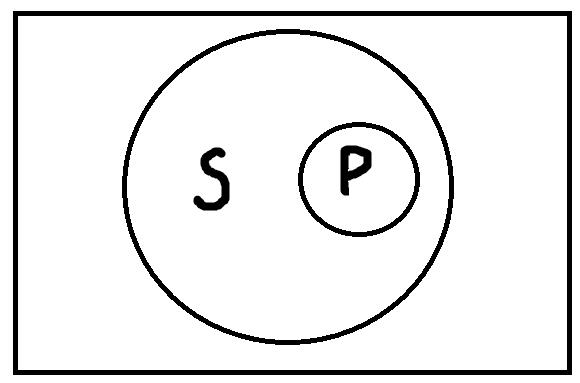
Единичноутвердительные высказывания формы «s есть P» истинны, только если термины s и P находятся в следующем отношении:
Другими словами, единичноутвердительные высказывания истинны, если точка, представляющая собой имя s, находится внутри кружочка, изображающего объём термина P. Например, возьмём высказывание «Лев Толстой проповедовал вегетарианство». «Лев Толстой» – это субъект, имя s. «Человек, проповедующий вегетарианство» – это предикат, термин P. Это высказывание истинно, так как точка s будет входить в объём термина P. Если же взять высказывание «Николай Гоголь – это великий русский композитор», то точка s, представляющая имя («Николай Гоголь»), не будет входить в объём термина P («великие русские композиторы»). Поэтому это высказывание ложно.
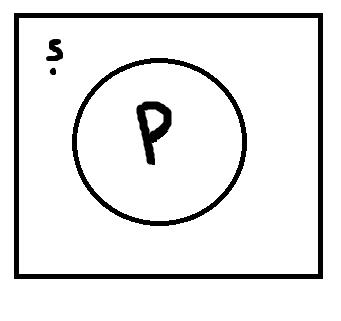
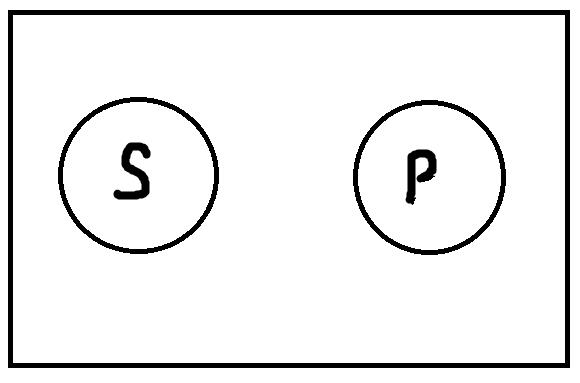
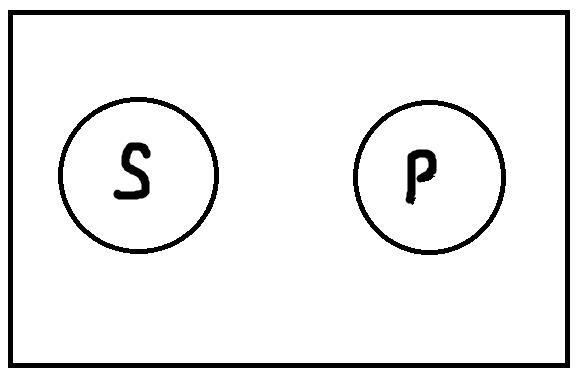
Единичноотрицательные высказывания, имеющие форму «s не есть P» истинны, если термины s и P находятся в следующем отношении:
Как видно из рисунка, здесь имеет место ситуация, прямо противоположная условиям истинности единичноутвердительных высказываний. Если точка, представляющая имя s, находится вне объёма термина P, то высказывание истинно. В обратном случае, оно ложно. Пример истинного единичноотрицательного высказывания: «Александр Пушкин никогда не был во Франции». Ложным единичноотрицательным высказыванием будет: «Иван Бунин не получил Нобелевскую премию по литературе».
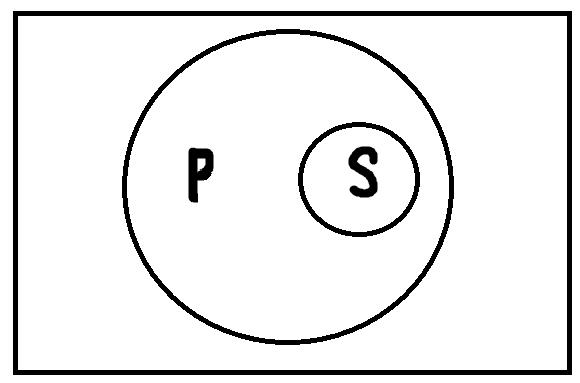
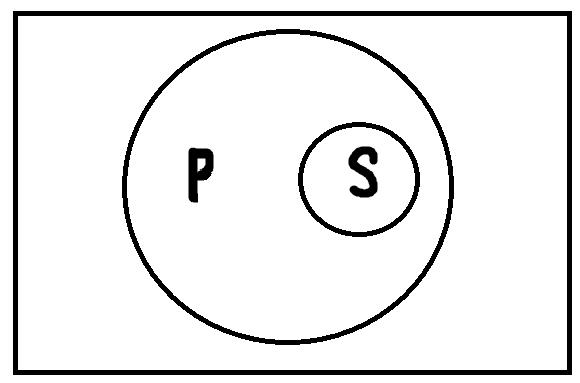
Общеутвердительные высказывания формы «Все S есть P» истинны, если термины S и P находятся в одном из следующих отношений:
Первый рисунок изображает отношение равнообъёмности, второй – обратного подчинения. Если объёмы двух терминов совпадают (S и P делят один кружочек) или объём термина S полностью входит в объём термина P (кружочек S полностью включается в P), то общеутвердительное высказывание истинно. Если термины S и P находятся в каком-либо другом отношении, то общеутвердительные высказывания не могут быть истинными. В качестве иллюстрации истинных высказываний можно привести: «Все хвойные растения имеют шишки», «Все киты – это млекопитающие». Пример ложных высказываний: «Все политики – обманщики», «Все девушки мечтают выйти замуж за миллионера». В этих примерах термины, обозначающие субъект и предикат, не находятся ни в одном из указанных выше отношений.
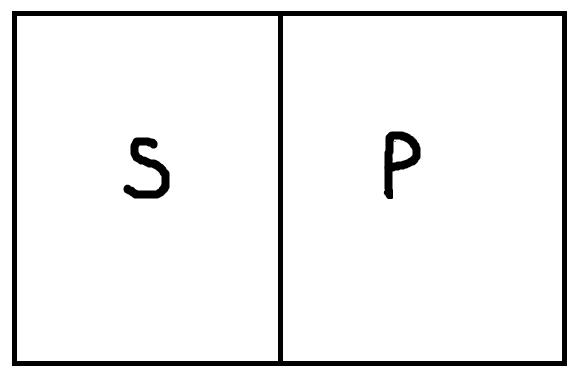
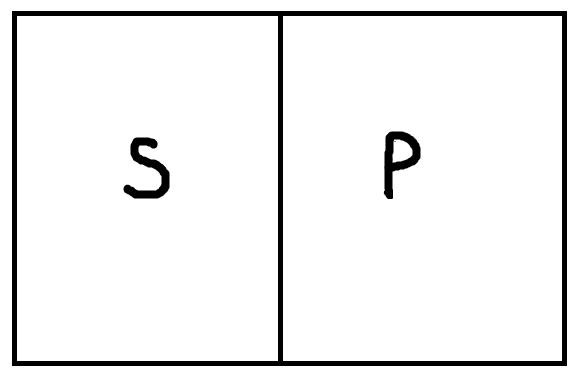
Общеотрицательные высказывания, имеющие форму «Ни один S не есть P» истинны, только если термины S и P находятся в следующих отношениях:
На первом рисунке представлено отношение противоречия, а на втором – соподчинения. Как видно, у S и P нет общих элементов, их объёмы не пересекаются. К примеру, истинными будут высказывания: «Ни один павлин не относится к числу певчих птиц», «Ни один человек младше восемнадцати лет не является совершеннолетним в России». Пример ложного высказывания: «Ни один гуманитарий не разбирается в математике». Высказывание ложно, так как термины «гуманитарий» и «люди, разбирающиеся в математике» не находятся ни в отношении противоречия, ни в отношении соподчинения.
Частноутвердительные высказывания формы «Некоторые S есть P» истинны, если термины S и P находятся в следующих отношениях:
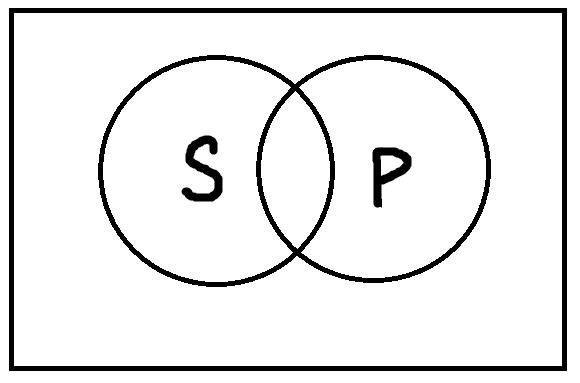
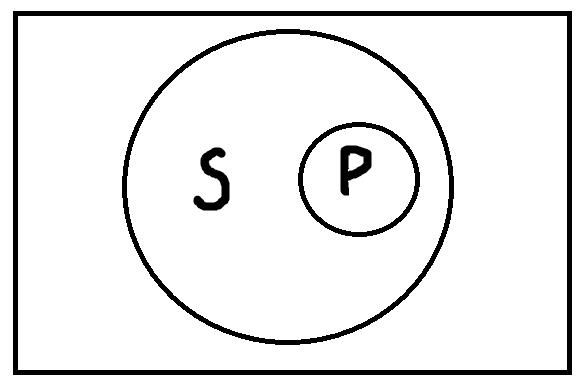
Частноутвердительные высказывания будут ложными, только если термины S и P находятся в отношении противоречия или соподчинения: «Некоторые тракторы – это самолёты», «Некоторые ложные высказывания истинны».
Частноотрицательные высказывания типа «Некоторые S не есть P» истинны, если термины S и P находятся в следующих отношениях:
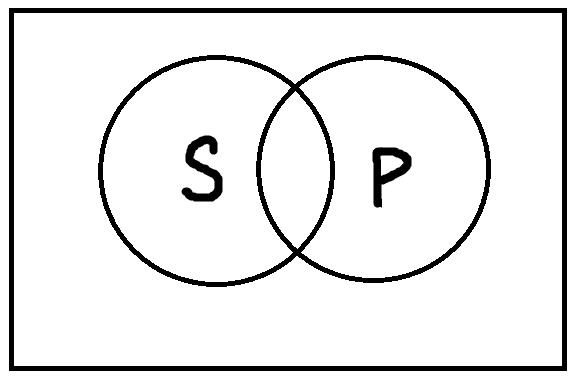
Это отношения: пересечения, дополнительности, включения, противоречия и соподчинения. Очевидно, что первые три отношения совпадают с тем, что было верно и для частноутвердительных высказываний. Все они как раз представляют случаи, когда некоторые S есть P, и в то же время некоторые S не есть P. Примеры подобных истинных высказываний: «Некоторые здоровые люди не употребляют алкоголь», «Некоторые наши работники из категории младше сорока ещё не достигли возраста и двадцати пяти», «Некоторые деревья не являются вечнозелёными».
По тем же причинам, по которым отношения равнообъёмности и обратного подчинения представляли собой условия истинности для частноутвердительных высказываний, отношения противоречия и соподчинения будут верны для частноотрицательных высказываний. Из высказывания, имеющего форму «Некоторые S не есть P» нельзя логично вывести высказывание «Некоторые S есть P». Однако из высказывания «Все S не есть P» можно перейти к высказыванию «Некоторые S не есть P», так как на основании информации, которой мы обладаем обо всех элементах объёмов терминов S и P, можно сделать вывод и об их отдельных представителях. Поэтому верными будут высказывания: «Некоторые журналы не являются книгами», «Некоторые глупцы не являются умными» и т.п.
Частноотрицательные высказывания будут ложными, только если термины S и P находятся в отношениях равнообъёмности и обратного подчинения. Примеры ложных высказываний: «Некоторые рыбы не умеют дышать под водой», «Некоторые яблоки не являются фруктами».
Итак, мы выяснили, при каких условиях высказывания той или иной формы будут истинными и ложными. При этом стало понятно, что не всегда истинность и ложность высказываний с логической точки зрения совпадает с нашими интуитивными представлениями. Иногда одинаковые на первый взгляд высказывания оцениваются совершенно по-разному, так как за ними скрываются разные логические формы и, следовательно, разные отношения между входящими в них терминами. Эти условия истинности важно запомнить. Они пригодятся, когда в следующем уроке мы научимся складывать высказывания в цепочки рассуждений и будем пытаться найти такие формы умозаключений, которые будут всегда правильными.
Игра «Пересечение множеств»
В этом упражнении вам нужно внимательно прочитать текст задания и правильно расположить множества, соответствующие понятиям.
Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.
Упражнения
Прочитайте следующие категориальные атрибутивные высказывания. Определите, к какому типу они относятся. С помощью диаграмм покажите, истинны они или ложны.
Проверьте свои знания
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.