что такое устранимая особая точка

Что такое устранимая особая точка

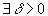
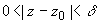
Точка z₀, принадлежащая области комплексных чисел, называется изолированной особой точкой функции f(z), если такая, что f(z) является однозначной аналитической функцией в (в самой точке аналитичность f(z) нарушается).

ПРИМЕР 1. Отыскание особых точек рациональной дроби.

ПРИМЕР 2. Определение типа особых точек.

ПРИМЕР 3. Определение типа особой точки.

Для того чтобы особая точка функции была полюсом, необходимо и достаточно, чтобы главная часть ряда Лорана функции в окрестности этой точки содержала конечное число членов.

Ряд Лорана функции f(z) в случае z₀-полюс имеет вид:
(2)
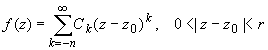
если z₀ принадлежит области комплексных чисел.

Номер старшего члена главной части ряда Лорана функции в ее разложении в окрестности полюса называется порядком полюса.
Так, точка z₀ является полюсом порядка n функции f(z), если в разложении (2) 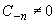, C_k = 0 при k

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Источник

Что такое устранимая особая точка

ОСОБЫЕ ТОЧКИ И ИХ КЛАССИФИКАЦИЯ

Точка аС z называется изолированной особой точкой однозначного характера функции f ( z ), если f ( z ) аналитическая и однозначная (регулярная) в кольце < z :0 z – a | r >, а в самой точке а не определена.

Бесконечно удаленная точка называется изолированной особой точкой однозначного характера функции f ( z ), если f ( z ) регулярна в некоторой окрестности < R z | z= и функция

имеет в точке x = 0 изолированную особую точку однозначного характера.

В зависимости от поведения функции f ( z ) вблизи точки а различают следующие три типа особых точек.

Изолированная особая точка а функции f ( z ) называется

а) устранимой особой точкой, если существует конечный предел

в) существенно особой точкой, если

Заметим, что типы особых точек z = функции f ( z ) и x = 0 функции j(x) совпадают, ибо

f ( a )= f ¢ ( a )=…= f ( m-1 ) ( a ) =0,

f (m) ( a ) 0.

При т =1 точка а называется простым нулем функции f ( z ), при m >1-кратным.

Порядком (или кратностью) полюса функции g ( z ) в точке а называется кратность нуля в точке а регулярной функции

, где P ( z ) и Q ( z ) – полиномы, не имеющие общих корней, то корни полинома Q ( z ) (и только они) являются полюсами функции f ( z ).

Порядок полюса f ( z ) совпадает с кратностью соответствующих корней полинома Q ( z ).

Точка z= называется нулем кратности m 1 для функции f ( z ), регулярной в этой точке, если функция

имеет нуль кратности т в точке x =0.

Если z=а – изолированная особая точка однозначного характера для функции f ( z ), то f ( z ) регулярна в некотором кольце < z : 0 z-a | r >и ее можно разложить в ряд Лорана, сходящийся в этом кольце,

.

Тип изолированной особой точки однозначного характера определяется видом лорановского разложения функции в проколотой окрестности этой точки.

2. Для того чтобы точка а была полюсом функции f ( z ), необходимо и достаточно, чтобы главная часть лорановского разложения функции f ( z ) в окрестности этой точки содержала лишь конечное число членов (причем полюсом порядка т ³ 1, если главная часть имеет вид

, где с т 0.

3. Точка а тогда и только тогда является существенно особой, когда главная часть лорановского разложения функции f ( z ) в окрестности этой точки содержит бесконечно много отличных от нуля членов.

Разложение функции f ( z ) в окрестности бесконечно удаленной точки в ряд Лорана имеет вид

Опираясь на приведенные критерии типа особой точки и определение вычета в точке z = , рекомендуем читателю сформулировать соответствующие утверждения для точки z = .

Источник

Ряды Лорана. Изолированные особые точки и их классификация

По этой ссылке вы найдёте полный курс лекций по математике:

Любую функцию f(z), однозначную и аполитичную в круговом котьце можно представить в этом кольце в виде суммы сходящегося ряда коэффициенты Сп которого определены однозначно и вычисляются по формулам где 7р — окружность радиуса м Зафиксируем внутри кольца Я произвольную точку z. Построим окружности центрами в точке го, радиусы которых удовлетворяют неравенствам и рассмотрим новое кольцо По интегральной теореме Коши для многосвязной области имеем Преобразуем отдельно каждый из интегралов в сумме (8).

Возможно вам будут полезны данные страницы:

Совокупность членов этого ряда с неотрицательными степенями называется правильной частью ряда Лорана, а с отрицательными — его главной частью.

Следовательно, имеется три кольцевых области, с центром в точке го = 0. в каждой из которых функция /(г) является аналитической: а) круг кольцо внешность круга (рис.27). Найдем лорановские разложения функции /(z) в каждой из этих областей. Представим /(z) в виде суммы элементарных дробей а) Круг Преобразуем соотношение (16) следующим обра- Используя формулу для суммы членов геометрической прогрессии, получим Подставим найденные разложения в формулу (17): Это разложение является рядом Тейлора функции /(z). б)

Эгот пример показывает, что для одной и той же функции f(z) лорановское разложение, вообще говоря, имеет различный вид для разных колец. Пример 3. Найти разложение 8 ряд Лорана функции Ряды Лорана Изолированные особые точки и их классификация а кольцевой области А Воспользуемся представлением функции f(z) в следующем виде: и преобразуем второе слагаемое Используя формулу для суммы членов геометричесхой прогрессии, получим Подставляя найденные выражения в формулу (22), имеем Пример 4.

в окреслюсти тонки zq = 0. Для любою комплексного имеем Положим Это разложение справедливо для любой точки z Ф 0. В данном случае кольцевая область представляет собой всю комплексную плоскость с одной выброшенной точкой z — 0. Эту область можно определить следующим соотношением: Данная функция является аналитической в области Из формул (13) для коэффициентов ряда Лорана такими же рассуждениями, что и в предыдущем параграфе, можно получить неравенства Kouiw.

Изолированная особая точка называется: 1) устранимой, если существует конечный 2) пмюсач, если 3) существенно особой точкой, если функция f(z) не имеет предела при Тип изолированной особой точки тесно связан с характером лорановского разложения функции выколотым центром го. Теорема 16. Изолированная особая точка z0 функции f(z) является устранимой особой точкой в том и только в тач случае, когда лорановское разложение функции f(z) в окрестности точки zo не содержит главной части, т. е. имеет вид.

Теорема 17. Изолированная особая точка zq функции f(z) является устранимой тогда и только тогда, когда функция J(z) ограничена в некоторой проколотой окрестности точки zq, Згмечаи не. Пусть го — устранимая особая точка функции /(г). Полагая мы получим, чтофункция /(г) аналитична в некотором к руге с центром в точке го.

Это определяет название точки — устранимая. Теорема 18. Изолированная особая точка zq функции f(z) является полюсом в том и только в том случае, когда главная частьлорановскогоразложения функции f(z) в окрестности точки содержит конечное (и положительное) числоотличных от нуля членов, т. е. имеет вид 4 Пусть z0 — полюс. Так как то существует проколотая окрестность точки z0, в которой функция f(z) аналитична и отлична от нуля.

Из теорем 16 и 18 вытекает следующее утверждение. Теорема 19. Изолированная особая тонка является существенно особой в том и только в том случае, когда главная часть лорановского разложения в проколотой окрестности этой точки содержит бесконечно много отличных от нуля членов. Пример 5. Особой точкой функции является zo = 0. Имеем Ряды Лорана Изолированные особые точки и их классификация.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник