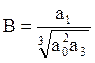что такое устойчивость системы автоматического регулирования сар
Что такое устойчивость системы автоматического регулирования сар
Устойчивостью систем автоматического регулирования называют их способность поддерживать заданный регулируемый режим работы системы с определенной точностью и восстанавливать его в случае нарушения. Таким образом, об устойчивости системы регулирования можно судить по характеру свободного переходного процесса.
Следовательно, двигатель, оборудованный автоматическим регулятором, будет работать устойчиво только в том случае, если все корни характеристического уравнения (722) или (724) являются отрицательными действительными или комплексными сопряженными с отрицательной действительной частью. Наличие хотя бы одного положительного корня или положительной действительной части одной из пар комплексных сопряженных корней делает исследуемую систему регулирования двигателя неустойчивой.
Рассматривая действительные корни характеристического уравнения (724) в качестве частного случая комплексных сопряженных корней, все корни уравнения можно расположить на комплексной плоскости (рис. 250) с мнимой осью ординат и действительной осью абсцисс. В этом случае каждому корню на выбранной координатной плоскости соответствует вполне определенная точка, а сам корень изображается в виде вектора, длина которого является модулем комплексного числа, а угол наклона, отсчитанный от положительного направления действительной оси, — аргументом (или фазой).
Система автоматического регулирования устойчива только в том случае, если все точки, соответствующие корням характеристического уравнения, находятся в левой полуплоскости расположения корней (заштриховано).
К эксплуатации могут быть пригодны только те двигатели, системы автоматического регулирования которых являются устойчивыми на всех рабочих режимах, поэтому оценка системы на устойчивость является одной из первостепенных задач.
Отказ от линеаризации характеристик приводит к нелинейным дифференциальным уравнениям.
Устойчивость системы регулирования без ограничения отклонений параметров получают, как правило, в результате исследования нелинейных дифференциальных уравнений. Такая устойчивость называется устойчивостью в большом.
Специальными исследованиями установлено, что по полностью линеаризованным уравнениям двигателя и регулятора можно не только правильно оценить устойчивость системы регулирования, но и в определенном (довольно большом) диапазоне отклонений параметров построить переходные процессы, хорошо согласующиеся с переходными процессами, полученными экспериментальным путем. Это свидетельствует о достаточной достоверности результатов анализа в малом и о практической их ценности. Однако необходимо отметить, что возможны случаи, когда система автоматического регулирования, устойчивая в малом, будет неустойчивой в большом.
Устойчивость систем автоматического регулирования



Основное требование к САР состоит в том, что система должна быть устойчивой. Система автоматического регулирования называется устойчивой, если регулируемая величина, получившая отклонение от заданного значения под действием внешних возмущений, с течением времени в установившемся режиме становится равной заданному значению или близкому к нему с некоторой ошибкой.
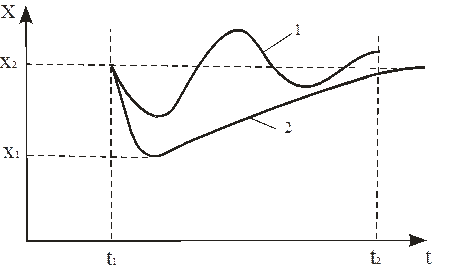
Объект регулирования находится под воздействием внешних возмущений; результат этих возмущений – отклонение регулируемой величины от заданного значения. Регулятор воспринимает это отклонение и воздействует на объект так, чтобы устранить появившееся отклонение регулируемой величины. В правильно созданной САР после появления отклонения регулируемая величина с течением времени принимает заданное значение или близкое к нему (рис. 1.12).
Рис. 1.12. Характер изменения регулируемой величины во времени в устойчивой САР:
1 – апериодический сходящийся переходный процесс; 2 – колебательный процесс
Характер изменения регулируемой величины во времени (апериодический или колебательный) зависит от свойств объекта и регулятора. Кривая 1 рис. 1.12 может характеризовать, например, изменение уровня воды в барабане котла: до момента времени 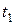
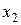
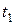
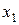
Рассмотренный процесс в САР с момента времени 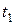
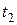
|
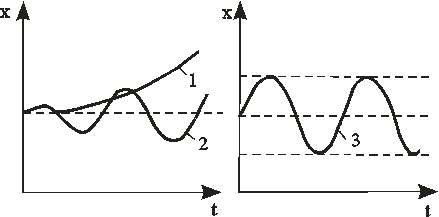
В неустойчивых САР регулируемая величина с течением времени удаляется от своего заданного значения и переходный процесс носит расходящийся характер (рис. 1.13а).
|
Рис. 1.13. Переходный процесс в неустойчивой САР:
1 – апериодический расходящийся; 2 – колебательный расходящийся; 3 – колебательный незатухающий
Переходный процесс в САР может иметь характер незатухающих колебаний с постоянной амплитудой (рис. 1.13б). Такие САР относят также к неустойчивым, и они не пригодны к эксплуатации.
Устойчивость автоматических систем



Подобно тому, как употребляется термин «устойчивость» в общераспространенном понимании, в автоматике под этим термином тоже в некоторой степени подразумевается способность какой-либо системы противостоять факторам, выводящим систему из равновесия. Строгая формулировка такова.
Устойчивость – это способность системы приходить к состоянию равновесия после прекращения действия факторов, которые вывели её из равновесия. Состояние равновесия характеризуется неизменностью во времени регулируемых величин. Если система не приходит к состоянию равновесия, а бесконечно от него удаляется, она не устойчива. Неустойчивые системы не могут эксплуатироваться, поскольку в них происходит неконтролируемое изменение регулируемых величин. Как правило, потеря системой устойчивости приводит к авариям объекта регулирования, причем часто катастрофического характера. Как примеры можно указать на опрокидывание потерявших остойчивость судов, разрушение двигателей («разнос»), взрывы на предприятиях химического производства и т. д. Таким образом, требование устойчивости является обязательным для любой работоспособной системы. Следует отметить, что потеря устойчивости САР может произойти вследствие изменения её свойств, вызванного как износом или отказом элементов, так и (весьма нередко) неквалифицированными действиями человека при попытке изменить настройку системы либо в процессе выполнения профилактических мероприятий. Заметим также, что понятие устойчивости имеет качественный характер, но не количественный. Так, о системе можно сказать, что она устойчива либо неустойчива, но нельзя говорить, что система «более» либо «менее» устойчива.
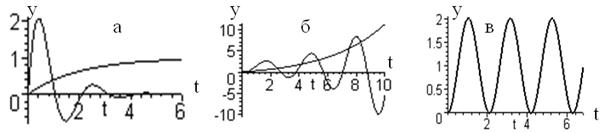
Характер переходных процессов в устойчивых и неустойчивых системах при действии внешних факторов можно видеть на рис. 6.1. Устойчивые системы по окончании переходного процесса приходят к некоторому установившемуся значению регулируемой величины (рис. 6.1, а), в неустойчивых системах (рис. 6.1, б) регулируемая величина неограниченно изменяется. Если же процесс в системе носит характер установившихся колебаний (как граничный между затухающими и расходящимися колебаниями), то говорят, что система находится на границе устойчивости (рис. 6.1, в). Понятно, что только вариант (6.1, а) приемлем для практического применения. Таким образом, внешним признаком устойчивой системы является ограниченность регулируемой величины: у = огр.
Рис. 6.1 Переходные процессы в системах:
а – устойчивых; б – неустойчивых;
в – САР на границе устойчивости.
Исходными данными для решения задачи об устойчивости системы является её математическое описание. Первое решение такой задачи, не лишенное недостатков, дал английский физик Джеймс Максвелл (1868).
Оценка устойчивости САР по корням её
характеристического уравнения (теорема Максвелла)
Пусть система описывается дифференциальным уравнением
| (anp n + an-1p n-1 + …+ a1p + a0) y = bx. | (6.1) |
Решение его, как любого линейного уравнения, ищется в виде
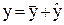
где 
| (anp n + an-1p n-1 + …+ a1p + a0) y=0, | (6.2) |
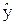
Как всегда, частное решение – это значение регулируемой величины на новом установившемся режиме, вызванном воздействием х=х0:
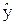
Подстановка в (6.1) даёт условие установившегося режима:
а0
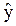
В реальных условиях воздействие всегда ограничено по величине, и поэтому частное решение ограничено. Отсюда следует важный вывод: правая часть дифференциального уравнения не влияет на устойчивость линейной системы, следовательно, от внешних воздействий не зависит, обладает система свойством устойчивости или нет. Таким образом, устойчивость САР определяется только видом левой части её уравнения. Общее решение:
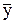 = C1exp(p1t)+ C2exp(p2t)+…+ Cnexp(pnt), = C1exp(p1t)+ C2exp(p2t)+…+ Cnexp(pnt), | (6.3) |
Поскольку постоянные интегрирования есть ограниченные величины, очевидно, что ограниченность общего решения зависит от вида функций
то есть от корней характеристического уравнения. В общем случае среди корней могут быть вещественные, комплексные и мнимые. Каждому виду корней в выражении (6.3) соответствует определенный вид слагаемого и, естественно, требуется ограниченность каждого из них (табл. 6.1).
Третий случай даёт незатухающую составляющую в общем решении, и если остальные составляющие являются сходящимися, то система находится на границе устойчивости. Это свойство часто используется при анализе устойчивости САР. Выражение в квадратных скобках есть ограниченная величина. Таким образом, ограниченность общего решения зависит от того, ограничены или нет функции exp(akt) для всех k Î[1,n]. При очевидном t > 0 для этого требуется, чтобы
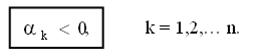 | (6.4) |
| Вид корня | Вид слагаемого |
| вещественный pk = ak | Ckexp(akt) |
| комплексные pk,k+1=ak±wki | exp(akt)[Ckcos(wkt)+Ck+1sin(wkt)] |
| Mнимые pk,k+1=±wki | Ckcos(wkt)+Ck+1sin(wkt) |
Теорема Максвелла: для устойчивости линейной системы необходимо и достаточно, чтобы вещественные части всех корней характеристического уравнения этой системы были отрицательны.
Частные случаи: достаточные условия устойчивости систем первого и второго порядков.
Характеристическое уравнение САР 1 порядка
Характеристическое уравнение САР 2 порядка
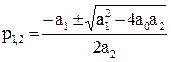
Анализ этого выражения приводит к заключению, что и здесь достаточным условием устойчивости является положительность всех коэффициентов характеристического уравнения, а если коэффициенты отличаются по знаку, то система неустойчива.
Устойчивость САР высоких порядков.
Для устойчивости систем 3 и более высоких порядков требование положительности всех коэффициентов характеристического уравнения является необходимым, но не достаточным. Другими словами, если все корни имеют отрицательные вещественные части, то все коэффициенты будут положительны, но обратное утверждение не справедливо.
Вычисление корней уравнений третьей и четвертой степеней связано со значительными трудностями, а корни уравнений пятой и более высоких степеней согласно теореме Абеля не могут быть выражены через коэффициенты с использованием знаков алгебраических действий и операции извлечения квадратного корня. Это значит, что при несомненной справедливости теоремы Максвелла её использование ограничено. Поэтому разработаны такие способы анализа устойчивости систем, когда не требуется нахождение корней. Все эти способы получили название критериев устойчивости. Здесь мы считаем возможным рассмотреть наиболее употребительные из них.
Критерий Гурвица (1895).
Уравнение системы порядка n
будет иметь корни с только отрицательными вещественными частями при выполнении следующих требований:
все коэффициенты характеристического уравнения и все диагональные миноры определителя Гурвица должны быть положительны:
Правило составления определителя Гурвица.
По главной диагонали располагаются последовательно коэффициенты уравнения, начиная со второго слева. Расположение коэффициентов в колонках в направлении сверху вниз соответствует их расположению в уравнении в направлении справа налево. Места отсутствующих коэффициентов заполняются нулями. Диагональные миноры – это определители, получающиеся из определителя Гурвица последовательным вычеркиванием правых колонок и нижних строк. Например, минор с индексом (n-3) выглядит так:


Заметим, что в принятом нами порядке индексации индекс минора совпадает с индексом коэффициента, стоящего в его нижнем правом углу.
Модификация критерия Гурвица – критерий Льенара-Шипара. Авторы этого критерия установили, что можно обойтись меньшим количеством неравенств, чем это требуется по критерию Гурвица. Согласно этому критерию, требование положительности всех диагональных миноров заменяется требованием положительности диагональных миноров с нечетными индексами.
Критерий Михайлова (1938).
Пусть собственный оператор системы имеет вид
| D(p) = anp n + an-1p n-1 + … + a1p + a0. | (6.5) |
| D(p) = an(p – p1)(p – p2)…(p – pn). | (6.6) |
Произведём замену p = iw:
2. Производится подстановка р = iw:
3. Выделяются вещественная и мнимая части:
4. Приняв для w ряд значений в диапазоне (0, ¥), рассчитываются соответствующие значения координат вектора кривой Михайлова и строится эта кривая.
5. По виду кривой делается заключение об устойчивости.
Примечание. Для любой системы кривая Михайлова уходит в бесконечность в той четверти, каков порядок системы, и это свойство следует использовать при выборе диапазона изменения w.
Критерий Найквиста (1932).
Этот критерий позволяет судить об устойчивости замкнутой САР по виду амплитудно-фазовой характеристики этой системы в разомкнутом состоянии. Между АФХ разомкнутой системы Wp и замкнутой W3 соотношения таковы:
Рассмотрим схему САР на рис. 6.5. Система, имеющая передаточную функцию в разомкнутом состоянии Wp, замкнута единичной отрицательной главной обратной связью.
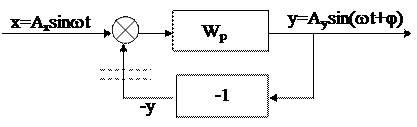 |
Рис. 6.5 Замыкание разомкнутой САР
Мысленно разорвём замкнутую цепь в месте, указанном пунктиром. Возбудим на входе гармонические колебания х. На выходе разомкнутой системы возникнут колебания
а на выходе звена обратной связи колебания будут иметь обратный знак, что можно трактовать как смещение по фазе на угол p:
Примем некоторую частоту, при которой фазовый сдвиг, получающийся в разомкнутой системе,
Замкнутая система будет устойчивой, если соответствующая разомкнутая система устойчива, и АФХ последней не охватывает точку с координатами (-1,0i) (рис. 6.6).
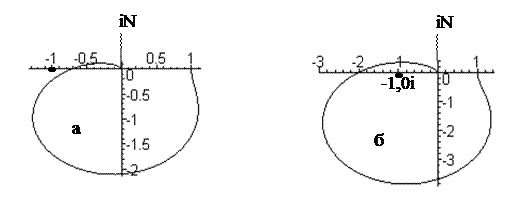 |
Рис. 6.6 АФХ разомкнутых систем:
б – замкнутая система неустойчива.
D- разбиение пространства параметров.
Этот способ анализа САР на устойчивость отличается от других тем, что даёт ответ не только на вопрос, устойчива САР или нет, но и позволяет определить для некоторых интересующих нас параметров системы области этих параметров, в которых САР сохраняет свойство устойчивости. Наиболее распространено D- разбиение по двум параметрам.
Пусть характеристическое уравнение САР имеет вид
| anp n +an-1p n-1 +…+Ap k +…+ Bp s +…+a1p+a0=0, | (6.8) |
где A и B- коэффициенты уравнения, для которых мы хотим найти те области, где САР устойчива. Выведем систему на границу устойчивости, для чего потребуем наличия чисто мнимых корней уравнения (3.76) p = iw:
| an(iw) n +an-1(iw) n-1 +…+A(iw) k +…+B(iw) s +…+a1(iw)+a0=0. | (6.9) |
Записанное слева комплексное число равно нулю по определению тогда, когда равны нулю его вещественная и мнимая части. Выделив их, получим:
| F1(A,w) = 0; F2(B,w) = 0. | (6.10) |
Иногда удаётся из этих уравнений исключить w, и тогда получают зависимость
Функция B = f(A) является границей устойчивости и отображает мнимую ось комплексной плоскости корней. Она делит область возможных по необходимому условию устойчивости значений А и В на области устойчивости и неустойчивости. Для выделения области устойчивости проще всего поступить так. Задаться в какой-нибудь области точкой с координатами (А=А1, В=В1) и с помощью какого-либо из рассмотренных ранее критериев проанализировать эту конкретную систему на устойчивость. Если результат окажется положительным, это означает, что вся область, к которой принадлежит выбранная точка, является областью устойчивости, и её штрихуют по границе с направлением штриховки внутрь. Если линия границы устойчивости имеет самопересечения, то по выходу из заштрихованной области штриховку продолжают с той же стороны по ходу по кривой. Типичным примером D- разбиения является рассматриваемый ниже критерий Вышнеградского.
Он распространяется на системы третьего порядка и в своё время был разработан в связи с необходимостью анализа САР частоты вращения вала паровой машины с центробежным регулятором прямого действия. Характеристическое уравнение системы
Выполнив замену переменной
приходим к выражению
| U 3 + AU 2 + BU + 1 = 0, | (6.12) |
называемому уравнением Вышнеградского, где коэффициенты
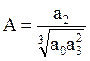
называются параметрами Вышнеградского.
Отметим прежде всего, что необходимые условия устойчивости выражаются в таком виде:
Выведем систему на границу устойчивости, для чего в уравнение (6.12) подставим р = iw:
(iw) 3 + A (iw) 2 + B iw + 1 = 0,
что после разделения вещественной и мнимой частей даёт
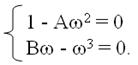 | (6.14) |
Из второго уравнения системы (6.14) подставим в первое w 2 = В, тем самым совместно с (6.13) получим условия границы устойчивости:
| А > 0, В > 0, АВ = 1. | (6.15) |
На диаграмме Вышнеградского рис. 6.7 кривая, называемая гиперболой Вышнеградского, является границей устойчивости, и она делит область возможных значений коэффициентов А и В на две части, одна из которых является областью устойчивости. Для обнаружения этой области рассмотрим заведомо устойчивую систему, корни характеристического уравнения которой
Тогда характеристический полином можно представить в виде
откуда А = 3, В = 3. Этими координатами определяется точка М на диаграмме, следовательно, область выше гиперболы Вышнеградского есть область устойчивости. Тогда условия устойчивости записываются так:
Устойчивость линейных САР. Признаки устойчивости. Запасы устойчивости линейных САР.
Идентификация статических объектов. Планирование эксперимента. Полный факторный эксперимент.
Планирование эксперимента
Большинство научных исследований связано с экспериментом. Он проводится в лабораториях, на производстве, на опытных полях и т.д. Эксперимент может быть физическим, психологическим или модельным. Он может проводиться как на самом объекте так и на модели. Модель, как известно, может отличаться от реального объекта масштабом, а иногда природой (пример).
При этом существенно следующее:
1) стремление к минимизации общего числа опытов;
3) использование математического аппарата, формализующего многие действия эксперимента;
4) выбор чёткой стратегии, позволяющей принимать обоснованные решения после каждой серии экспериментов.
Задачи, для решения которых может использоваться планирование эксперимента (ПЭ), чрезвычайно разнообразны:
1) поиск оптимальных условий;
2) построение интерполяционных формул;
выбор существенных факторов;
3) уточнение констант теоретических моделей.
Задачи поиска оптимальных условий являются одними из наиболее распространенных научно-технических задач. Они возникают в тот момент, когда установлена возможность проведения процесса и необходимо найти наилучшие условия его реализации.
Для описания объекта исследования удобно воспользоваться понятием «черного ящика»:
|
Входы: Выходы:







| |
|
Планирование эксперимента предполагает активное вмешательство в процесс и возможность выбора в каждом опыте тех уровней факторов, которые представляют интерес. Поэтому такой эксперимент называется активным. Объект, на котором возможен активный эксперимент, называется управляемым.
На практике нет абсолютно управляемых объектов. На реальный объект обычно действуют как управляемые, так и неуправляемые факторы. Неуправляемые факторы влияют на воспроизводимость эксперимента и являются причиной её нарушения. Если требования воспроизводимости не выполняются, приходится обращаться к активно-пассивному эксперименту.
Результаты эксперимента используются для получения математической модели объекта исследований, которая представляет собой уравнение, связывающее, например, оптимизации и факторы. Такое уравнение называют функцией отклика.
Параметр оптимизации
При планировании экстремального эксперимента очень важно определить параметр, который нужно оптимизировать. Сделать это совсем не просто, как кажется на первый взгляд. Цель исследования должна быть сформулирована очень четко и допускать количественную оценку. В зависимости от объекта и цели исследования параметры оптимизации могут быть очень разнообразными.
Рис.2 Классификация параметров оптимизации
1) эффективным с точки зрения достижения цели;
3) количественным и выражаться одним числом;
4) статически эффективным (точные измерения);
5) имеющим физический смысл, простым и легко вычисляемым;
Факторы
После того как выбран объект исследования и П.О., нужно включить в рассмотрение все существующие факторы, которые влияют на процесс. Если какой-либо существующий фактор не учтен, то это может привести к неприятным последствиям. Чем больше факторов, то тем больше опытов необходимо провести, так как 
2. Планировать эксперимент можно только в том случае, если уровни факторов подчиняются воле экспериментатора.
3. Факторы должны непосредственно воздействовать на объект исследования. Трудно управлять фактором, если он является функцией других переменных, но в планировании эксперимента могут участвовать сложные факторы, такие, как логарифмы, соотношения и т.д. Факторы должны быть определены операционально.
5. Точность фиксации Ф. должна быть высокая, степень точности определяется диапазоном изменения факторов.
Выбор модели
В качестве примера запишем модель в форме полинома для 2 х факторов. Полином нулевой степени:
Полином первой степени:
Полином второй степени:
Выбор основного уровня

В разных случаях мы располагаем различными сведениями об области наилучших условий. Если имеются сведения о координатах одной наилучшей точки и нет информации о границах определения факторов, то остается рассматривать эту точку в качестве основного уровня. Аналогичное решение принимается, если границы известны и наилучшие условия лежат внутри области. На рис.2. Изображена область определения для 2 х факторов. Кружком отмечены наилучшие условия, известные из априорной информации. Чтобы правильно выбрать основной уровень следует пользоваться блок-схемой рис. 4.
Ошибки параллельных опытов
Каждый эксперимент содержит элемент неопределенности вследствие ограниченности экспериментальных данных. Постановка повторных (параллельных) опытов не дает полностью совпадающих результатов, потому что всегда существует ошибка опыта (ошибка воспроизводимости). Эту ошибку и следует оценить по параллельным опытам. Для этого опыт воспроизводится по возможности в одинаковых условиях несколько раз и затем берется среднее арифметическое всех результатов. Среднее арифметическое Y равно сумме всех m отдельных результатов, делённой на количество параллельных опытов m
Как правило, ошибка опыта является суммарной величиной, результатом многих ошибок: ошибок измерения факторов, параметра оптимизации и т.д. Все ошибки принято разделять на 2 класса: систематические и случайные.
Схематическое изображение компонент ошибок измерений представлено на рис. 8.
Рис.8 Схематичное изображение компонент ошибки измерений
Для выявления грубых ошибок используют критерий Стьюдента: 
Значение t берут из таблицы t-распределения Стьюдента. Опыт считается бракованным, если экспериментальное значение t по модулю больше табличного значения.
Рандомизация опытов
Регрессионный анализ
Как только мы начинаем говорить о пригодности модели или о значимости коэффициентов, приходится вспоминать о статистике: и с этого момента МНК превращается в регрессионный анализ.
Регрессионный анализ, как всякий статистический метод, применим при определенных предположениях, постулатах.
Первый постулат
Второй постулат
Дисперсия Y не зависит от абсолютной величины Y.
Третий постулат
Значения факторов суть не случайные величины. Это утверждение практически означает, что установление каждого фактора на заданный уровень и его поддержание существенно точнее, чем ошибка воспроизводимости.
Устойчивость линейных САР. Признаки устойчивости. Запасы устойчивости линейных САР.
На любую систему автоматического регулирования всегда действуют различные внутренние и внешние возмущения, которые могут нарушить ее нормальную работу. Правильно спроектированная САР должна устойчиво работать при всех возмущениях. Определение устойчивости: под устойчивостью понимают способность системы возвращаться с определенной точностью к состоянию равновесия после устранения причин, выведенных систему из состояния равновесия.
Для пояснения смысла, понятия устойчивости положения равновесия системы, удобно воспользоваться следующим примером. Пусть имеется некоторая чаша, поставленная дном вниз (рис. 1).

а) Устойчивая система б) Неустойчивая система в) Граница устойчивости
На дне чаши (а) в положении равновесия 1 находится тяжелый шарик, который приложенный внешней силой может быть отклонен в положение 2. В определенный момент времени, принимаемый за нулевой, внешняя сила убирается. Шарик, предоставленный сам себе, из положения 2 устремится вниз, и по инерции проскочит положение 1. Затем, достигнув наивысшего положения, уже справа от точки 1, шарик снова будет двигаться вниз. Совершив несколько колебательных движений, шарик из-за наличия сил сопротивления остановится с некоторой точностью в положении равновесия 1, т.е. согласно определению имеет место устойчивость положения равновесия для кратности обозначаемая литерой У.
В случае, когда чаша поставлена дном вверх (б). Шарик снова находится в положении равновесия 1 и если к нему не прикладывать никаких сил, то в этом положении он будет находиться сколь угодно долго. Если же некоторой внешней силой переместить шарик в положение 2, а затем убрать эту силу, то шарик удалится от положения 1 на бесконечно большое расстояние и никогда в него не вернется. Такое положение равновесия называется и обозначается 
В третьем случае (в) изображено нейтральное положение равновесия или граница устойчивости. Если шарик, находящийся на горизонтальной поверхности в положении 1, с помощью внешней силы переместить в положение 2, а затем убрать эту силу, то шарик останется положении 2 до тех пор, пока к нему не будет приложена новая внешняя сила. Случай нейтрального положения равновесия, можно обнаружить и на рис. 1 а, если там не существует сил сопротивления. В этом случае шарик будет совершать незатухающие колебания вокруг положения равновесия 1.
Принцип устойчивости САР
Обратимся теперь к математической стороне вопроса. Любая система автоматического регулирования с входным сигналом (внешней силой) х и выходным сигналом z, имеющая передаточную функцию: 
может быть описана линейным неоднородным дифференциальным уравнением
п-го порядка с постоянными коэффициентам 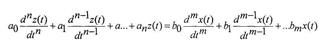
Решение этого неоднородного уравнения z(t,)состоит из общего решения zсв(t)-свободная составляющая однородного дифференциального уравнения 
если 
если 
если
Дифференциальному уравнению (3) соответствует характеристическое уравнение 
корни, которых могут быть либо вещественными (в том числе нулевыми) либо комплексно-сопряженными (в том числе чисто мнимыми).
Решение дифференциального уравнения (3) как известно, имеет следующий вид 
 |
Рассмотрим случаи, когда рi –вещественные корни

 |


 |
д) корни мнимые – не содержат действительной части
Рассмотрим все случаи на плоскости

Если все корни характеристического уравнения левые (либо отрицательные, либо имеют отрицательную вещественную часть), то система устойчива.
Система находится на границе устойчивости, если кроме левых корней есть еще корни, расположенные на мнимой оси.
Расположение корней зависит от коэффициентов характеристического уравнения, а следовательно, от параметров системы. a0p n + … + an = 0.
Если К2 > К1 – корни сдвинутся вправо.
Если К3> К2 – может привести к неустойчивости системы. При переходе корня навстречу штриховке устойчивость уменьшается.
Чем больше коэффициент усиления, тем меньше устойчивость (в большинстве случаев).
К3> Кгр>К2>К1. Кгр – параметр, при котором система выходит на границу устойчивости.
Система, у которой изменением параметра можно изменить устойчивость системы называется структурно-устойчивой системой; в противном случае, когда никакими изменениями параметров неустойчивую систему нельзя сделать устойчивой, называется структурно-неустойчивой системой.
Но корни характеристического уравнения можно вычислить только до 4 степени и вычисление их очень трудоемко.
Стодола – высказал условие, которое оказалось необходимым, но недостаточным.
Условие Стодола: Для устойчивости системы необходимо (но недостаточно), чтобы все коэффициенты характеристического уравнения были положительны (одного знака). Это условие будет необходимым и достаточным для уравнений 1 и 2 порядков.


Этой ситуации не возникнет, если САР работает не вблизи границе устойчивости. А в достаточном удалении от нее. Иначе говоря, САР должна обладать некоторым запасом устойчивости, обеспечивающим работоспособность ее в различных условиях эксплуатации.
Так как устойчивость замкнутой системы оценивается критерием Найквиста по расположению АФХ разомкнутой системы относительно критической точки, то в качестве меры оценки запаса устойчивости можно принять расстояние между АФХ Wp(jω) и критической точки (-1, j0). Но положение АФХ Wp(jω) на комплексной плоскости для каждого значения частоты ω характеризуется фазой и модулем. Именно поэтому вводят понятия запасов устойчивости те модулю (амплитуде) и фазе.




С ростом Куст – запас устойчивости
по амплитуде уменьшается.
Для устойчивых систем ЗУФ положителен γ>0.
Для неустойчивых систем ЗУФ отрицателен γ1>0.