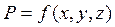что такое установившееся движение жидкости

Установившееся и неустановившееся движение.

Установившимся называют такое движение жидкости, при ко­тором скорость потока и давление в любой его точке не изменяются с течением времени и зависят только от ее положения в потоке, т. е. являются функциями ее координат. Примерами установившегося движения могут служить истечение жидкости из отверстия резервуара при постоянном напоре, а также поток воды в канале при не­изменном его сечении и постоянной глубине.

Неустановившимся называют такое движение жидкости, при ко­тором скорость движения и давление в каждой данной точке изме­няются с течением времени, т. е. являются функциями не только координат, но и времени. Примером неустановившегося движения служит истечении жидкости из отверстия резервуара при перемен­ном напоре. В этом случае в каждой точке сечения струи, выте­кающей из отверстия, скорость движения и давление изменяются во времени.

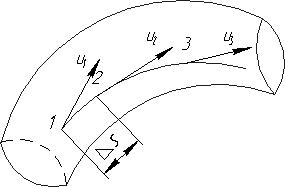
Линия тока. В точках 1, 2, 3 и т. д. потока, взятых на расстоя­нии ΔS друг от друга, проведем векторы u₁, u₂, u₃, показывающие значение и направление скоростей движения частиц жидкости в данный момент времени (рис. 1.18). Получим ломаную линию 1—2— 3и т. д. Если уменьшить длину от­резков ΔS, то в пределе ломаная линия станет кривой.

Рис. 1.18. Схематическое изображение линии тока в потоке

Эта кривая, называемая линией тока, характеризуется тем, что в данный момент времени во всех ее точках векторы скоростей бу­дут касательными к ней.

Элементарная струнка. Если в движущейся жидкости выделить бесконечно малый замкнутый контур и через все его точки провести линии тока, соответствующие данному моменту времени, получится как бы трубчатая непроницаемая поверхность, называемая трубкой тока.

Масса жидкости, движущейся внутри трубки тока, образует элементарную струйку.

Поток. Совокупность элементарных струек, представляющая собой непрерывную массу частиц, движущихся но какому-либо направлению, образует поток жидкости. Поток может быть пол­ностью или частично ограничен твердыми стенками, например в трубопроводе или канале, и может быть свободным, например струя, выходящая из сопла гидромонитора.

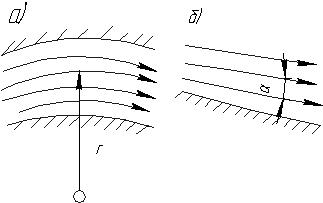
Рис. 1.19. Условия плавно из­меняющегося движения

Равномерным называют такое уста­новившееся движение жидкости, при котором живые сечения и средняя скорость потока не меняются по его длине. Примером равномерного дви­жения служит движение жидкости в цилиндрической трубе или в кана­ле неизменного сечения и постоянной глубины.

Неравномерным называют такое установившееся движение жид­кости, при котором живые сечения и средние скорости потока из­меняются по его длине. Примером неравномерного движения служит движение жидкости в конической трубе, в естественном русле, на перепаде.

При равномерном движении липни тока представляют собой систему прямых параллельных линий. Такое движение называется также параллельно–струйным. При движении жидкости в естествен­ных руслах живое сечение обычно непрерывно изменяется вдоль по­тока как по форме, так и по площади, и движение жидкости являет­ся установившимся неравномерным. Для облегчения изучения та­кого движения в гидравлике введено понятие плавно изменяюще­гося движения, которое характеризуется следующими свойствами (рис. 1.19):

Последнее свойство просто обосновывается. Если внутри плавно изменяющегося потока выделить частицу жидкости и спроекти­ровать все действующие на нее силы па плоскость живого сечения, то вследствие того, что скорости и ускорения почти перпендикуляр­ны живому сечению, силы инерции в уравнение равновесия не войдут; в связи с этим уравнение равновесия и закон распределения давления в плоскости живого сечения не будут отличаться от закона распределения давления в жидкости, находящейся в покое.

Напорным называется поток, у которого но всему периметру живого сечения жидкость соприкасается с твердыми стенками. Примером напорного потока может служить движение воды в водо­проводных трубах.

Безнапорным называется поток со свободной поверхностью. Примером безнапорного потока служит движение воды в реках, каналах и канализационных трубах.

1. В механике сплошной среды применяются два метода исследования – метод Л. Эйлера и метод Лагранжа.

В методе Л.Эйлера рассчитываются параметры сплошной среды в одних и тех же неподвижных точках пространства. Этот метод чаще всего используется в гидромеханике. Здесь данные расчета легко сравнивать с результатами экспериментов, т.к. все датчики (давления, температуры, скорости и т.п.) устанавливаются в неподвижных точках (труб, воздуховодов и т.п.).

В методе Лагранжа рассчитываются параметры (скорость, давление, температура) в одних и тех же подвижных точках среды. Метод Лагранжа более сложный. Он используется в научных исследованиях и в теории упругости. Здесь рассчитываются траектории частиц, т.к. здесь важно рассчитать перемещение точек тела. Здесь датчики параметров перемещаются вместе с точками твердого тела.

Источник

Виды движения жидкости

Основными видами движения жидкости являются: движение установившееся и неустановившееся, равномерное и неравномерное, напорное и безнапорное, сплошное и прерывистое.

Установившимся движением называется такое движение жидкости, при котором давление и скорость не изменяются во времени в каждой фиксированной точке пространства, через которую проходит жидкость.

,

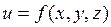
Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени, называется неустановившимся или нестационарным

,

.

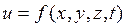
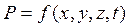
Примером неустановившегося движения может служить истечение жидкости из отверстия при переменном уровне ее в резервуаре: с понижением высоты столба жидкости скорость истечения уменьшается во времени.

Установившееся движение в свою очередь подразделяется на равномерное и неравномерное.

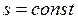
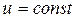
Равномерным называется такое установившееся движение, при котором живые сечения вдоль потока не изменяются: в этом случае ; средние скорости по длине потока также не изменяются, т.е. . Примером равномерного движения является: движение жидкости в цилиндрической трубе, в канале постоянного сечения при одинаковых глубинах.

Установившееся движение называется неравномерным, когда распределение скоростей в различных поперечных сечениях неодинаково; при этом средняя скорость и площадь поперечного сечения потока могут быть и достоянными вдоль потока. Примером неравномерного движения может быть движение жидкости в конической трубе или в речном русле переменной ширины.

Напорным называется движение жидкости, при котором поток полностью заключен в твердые стенки и не имеет свободной поверхности. Напорное движение происходит вследствие разности давлений и под действием силы тяжести. Примером напорного движения является движение жидкости в замкнутых трубопроводах (например, в водопроводных трубах).

Безнапорным называется движение жидкости, при котором поток имеет свободную поверхность. Примером безнапорного движения может быть: движение жидкости в реках, каналах, канализационных и дренажных трубах. Безнапорное движение происходит под действием силы тяжести и за счет начальной скорости. Обычно на поверхности безнапорного потока давление атмосферное.

Следует отметить еще один вид движения: свободную струю. Свободной струей называется поток, не ограниченный твердыми стенками. Примером может служить движение жидкости из пожарного брандспойта, гидромонитора, водопроводного крана, из отверстия резервуара и т. п. В этом случае движение жидкости происходит по инерции (т. е. за счет начальной скорости) и под действием силы тяжести.

Для упрощения выводов, связанных с изучением потока жидкости, вводится понятие о плавно изменяющемся движении жидкости.

Плавно изменяющимся называется такое движение жидкости, при котором кривизна струек незначительна (равна нулю или близка к нулю) и угол расхождения между струйками весьма мал (равен нулю или близок к нулю), т. е. практически поток жидкости мало отличается от параллельноструйного. Это предположение вполне оправдывается при изучении многих случаев движения жидкости в каналах, трубах и других сооружениях.

Отметим следующие свойства потока при плавно изменяющемся движении:

1. поперечные сечения потока плоские, нормальные к оси потока;

2. распределение гидродинамических давлений по сечению потока подчиняется закону гидростатики, т.е. гидродинамические давления по высоте сечения распределяются по закону прямой. Это свойство легко можно доказать, если внутри потока выделить частицу жидкости и спроектировать все действующие на нее силы на плоскость живого сечения. Вследствие того, что скорости и ускорения в этом случае будут перпендикулярны сечению, силы инерции в уравнение не войдут; поэтому уравнение равновесия и закон распределения давления в плоскости живого сечения не будет отличаться от такового для жидкости, находящейся в покое;

3. удельная потенциальная энергия (т. е. потенциальная энергия единицы веса жидкости) по отношению к некоторой плоскости сравнения для всех точек данного сечения потока жидкости есть величина постоянная.

Источник

Что такое установившееся движение жидкости

Если отдельные частицы абсолютно твердого тела жестко связаны между собой, то в движущейся жидкой среде такие связи отсутствуют. Движение жидкости состоит из чрезвычайно сложного перемещения отдельных молекул.

если угол в радианах, или

Поскольку скорость движения различных частиц жидкости отличается друг от друга, поэтому скорость движения и усредняется. В круглой трубе, например, скорость на оси трубы максимальна, тогда как у стенок трубы она равна нулю.

Течение жидкости может быть установившимся и неустановившимся. Установившимся движением называется такое движение жидкости, при котором в данной точке русла давление и скорость не изменяются во времени

Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени, называется неустановившимся или нестационарным

Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор скорости в данный момент времени направлены по касательной.

Из закона сохранения вещества и постоянства расхода вытекает уравнение неразрывности течений. Представим трубу с переменным живым сечением (рис.3.4). Расход жидкости через трубу в любом ее сечении постоянен, т.е. Q₁=Q₂= const, откуда

Таким образом, если течение в трубе является сплошным и неразрывным, то уравнение неразрывности примет вид:

Уравнение Даниила Бернулли, полученное в 1738 г., является фундаментальным уравнением гидродинамики. Оно дает связь между давлением P, средней скоростью υ и пьезометрической высотой z в различных сечениях потока и выражает закон сохранения энергии движущейся жидкости. С помощью этого уравнения решается большой круг задач.

Рассмотрим трубопровод переменного диаметра, расположенный в пространстве под углом β (рис.3.5).

Выберем произвольно на рассматриваемом участке трубопровода два сечения: сечение 1-1 и сечение 2-2. Вверх по трубопроводу от первого сечения ко второму движется жидкость, расход которой равен Q.

Кроме пьезометров в каждом сечении 1-1 и 2-2 установлена трубка, загнутый конец которой направлен навстречу потоку жидкости, которая называется трубка Пито. Жидкость в трубках Пито также поднимается на разные уровни, если отсчитывать их от пьезометрической линии.

Пьезометрическую линию можно построить следующим образом. Если между сечением 1-1 и 2-2 поставить несколько таких же пьезометров и через показания уровней жидкости в них провести кривую, то мы получим ломаную линию (рис.3.5).

Однако высота уровней в трубках Пито относительно произвольной горизонтальной прямой 0-0, называемой плоскостью сравнения, будет одинакова.

Если через показания уровней жидкости в трубках Пито провести линию, то она будет горизонтальна, и будет отражать уровень полной энергии трубопровода.

Для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли имеет следующий вид:

Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе:

и прочитать так: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть величина постоянная.

С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии:

Следовательно, согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении постоянна.

В этом случае уравнение Бернулли можно прочитать так: сумма геометрической, пьезометрической и скоростной высоты для идеальной жидкости есть величина постоянная.

Уравнение Бернулли для потока реальной жидкости несколько отличается от уравнения

Дело в том, что при движении реальной вязкой жидкости возникают силы трения, на преодоление которых жидкость затрачивает энергию. В результате полная удельная энергия жидкости в сечении 1-1 будет больше полной удельной энергии в сечении 2-2 на величину потерянной энергии (рис.3.6).

Потерянная энергия или потерянный напор обозначаются и имеют также линейную размерность.

Уравнение Бернулли для реальной жидкости будет иметь вид:

Из рис.3.6 видно, что по мере движения жидкости от сечения 1-1 до сечения 2-2 потерянный напор все время увеличивается (потерянный напор выделен вертикальной штриховкой). Таким образом, уровень первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного напора между сечениями 1-1 и 2-2.

Кроме этого в уравнении появились еще два коэффициента α₁ и α₂, которые называются коэффициентами Кориолиса и зависят от режима течения жидкости ( α = 2 для ламинарного режима, α = 1 для турбулентного режима ).

Потерянная высота складывается из линейных потерь, вызванных силой трения между слоями жидкости, и потерь, вызванных местными сопротивлениями (изменениями конфигурации потока)

Для измерения скорости в точках потока широко используется работающая на принципе уравнения Бернулли трубка Пито (рис.3.7), загнутый конец которой направлен навстречу потоку. Пусть требуется измерить скорость жидкости в какой-то точке потока. Поместив конец трубки в указанную точку и составив уравнение Бернулли для сечения 1-1 и сечения, проходящего на уровне жидкости в трубке Пито получим

Для измерения расхода жидкости в трубопроводах часто используют расходомер Вентури, действие которого основано так же на принципе уравнения Бернулли. Расходомер Вентури состоит из двух конических насадков с цилиндрической вставкой между ними (рис.3.7). Если в сечениях I-I и II-II поставить пьезометры, то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе.

Выражение, стоящее перед , является постоянной величиной, носящей название постоянной водомера Вентури.

Из полученного уравнения видно, что h зависит от расхода Q. Часто эту зависимость строят в виде тарировочной кривой h от Q, которая имеет параболический характер.

Источник

Виды движения жидкости. Неустановившееся и установившееся движение

Неустановившееся и установившееся движение

Величины гидродинамических давлений p и скоростей u в потоке жидкости в общем случае распределены неравномерно, они меняются при переходе от одной точки потока к другой, т.е. являются функциями координат (x, y, z).

Помимо того гидродинамические давления и скорости в одних и тех же фиксированных точках потока могут изменяться во времени как по величине, так и по направлению. Эти условия в общем виде могут быть записаны следующим образом:

Такой вид движения, при котором гидродинамические давления и скорости в каждой точке потока жидкости изменяются во времени по величине и направлению, называется неустановившимся движением.

Примерами неустановившегося движения жидкости могут служить:

— движение воды в реке во время весеннего половодья или при разрушении плотины, сопровождающееся изменением во времени уровня воды, ширины потока, скорости течения и давления в каждом сечении потока;

— истечение жидкости через отверстие в резервуаре при переменном уровне жидкости в нем, когда траектория струи и скорости истечения жидкости изменяются во времени;

— движение перекачиваемой жидкости во всасывающем или нагнетательном трубопроводе поршневого насоса.

Неустановившееся движение является самым общим и самым сложным видом движения жидкости, изучению которого посвящаются специальные курсы гидравлики.

Мы будем, в основном, рассматривать вопросы, касающиеся установившегося движения жидкости, при котором скорости и гидродинамические давления в каждой точке потока не изменяются во времени, а являются лишь функциями координат. При установившемся движении

Эти зависимости можно пояснить следующим образом. Пусть в данной фиксированной точке потока с координатами x, y, z в какой-то момент времени t частица жидкости будет обладать скоростью u (с проекциями на координатные оси u_x, u_y, u_z) и испытывать гидродинамическое давление p. Спустя некоторое время dt рассматриваемая частица переместится в какую-то другую точку, может приобрести другую скорость и испытывать другое давление. Но вторая частица жидкости, пришедшая на смену первой в фиксированную точку потока с координатами x, y, z будет обладать в точности такой же скоростью по величине и направлению и испытывать абсолютно такое же гидродинамическое давление, что и первая частица, когда она находилась в данной точке.

Следовательно, для полной характеристики установиваегося движения жидкости необходимо уметь находить функции (В – 3), которые будучи выражены в аналитической форме позволяют определить четыре неизвестных величины p, u_x, u_y, u_z в пространстве x, y, z.

Примерами установившегося движения жидкости являются:

— движение жидкости ( воды, бензина, масла ) в трубопроводе с постоянной скоростью течения;

— движение воды в канале постоянного сечения при постоянной глубине воды ;

— истечение жидкости через отверстие в резервуаре при постоянном уровне жидкости.

Источник

Гидродинамика. Характер изменения поля скоростей.

По характеру изменения поля скоростей во времени движения жидкости выделяют установившиеся и неустановившиеся, квазистационарное.

Установившееся движение – движение, характеризующееся тем, что в любом месте потока жидкости скорость (и давление) с течением времени претерпевают изменения, имеется в виду, что указанные показатели зависят исключительно от координат точки. Их величина изменяется лишь при переходе к другой точке пространства:

Неустановившееся движение – движение, характеризующееся тем, что в любом месте потока жидкости скорость с течением времени претерпевает изменения, т. е. выступает как функция координат и времени:

Квазистационарное движение – движение, характеризующееся тем, что изменчивость характеристик движения жидкости в течение отобранного временного отрезка не будет существенной, имеется в виду, что ее влияние лежит в пределах допускаемой точности решения, и его можно рассматривать как установившееся.

При описании установившегося движения жидкости выделяют равномерное и неравномерное.

Равномерным принято обозначать установившееся движение, при котором живые сечения вдоль потока неизменны: в этом случае w = const; средние скорости по длине потока также неизменны, т.е. v = const.

Установившееся движение принято обозначать неравномерным, когда выполняется условие, что распределение скоростей в различных поперечных сечениях разное; при этом средняя скорость и площадь поперечного сечения потока могут пребывать и постоянными вдоль потока.

Источник