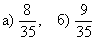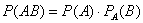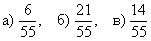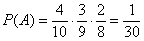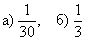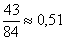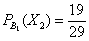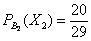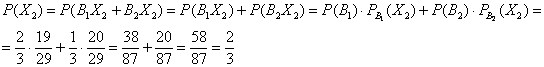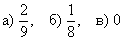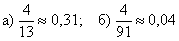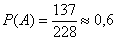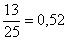что такое условная вероятность события
Условная вероятность. Формула Байеса
Условная вероятность. Формула Байеса
Условная вероятность является одним из важнейших понятий теории вероятностей.
Условная вероятность — вероятность наступления события А при условии, что событие В произошло.
Вероятность события А, вычисленная в предположении, что событие В уже произошло, обозначается 
Прежде чем привести формулу, позволяющую вычислить условную вероятность, проиллюстрируем это понятие с помощью кругов Эйлера:
Пусть для некоторого эксперимента красный круг обозначает множество всех возможных исходов. Зеленый круг обозначает множество исходов, благоприятствующих событию 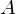
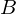
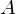
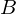
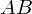
Как мы знаем, вероятностью события называется отношение числа благоприятных исходов к числу всех возможных исходов.
То есть вероятность события показывает, какую часть благоприятные исходы составляют от всех возможных исходов.
Если мы вычисляем вероятность события 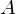
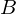
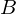
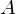
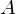
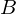
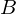
Пусть 

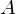


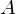
Пусть 

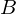


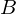
Пусть 

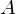
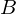


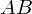
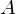
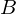
Тогда
Но по определению условной вероятности 

Заметим, что аналогично получим формулу для нахождения вероятности наступления события 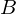
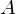

Очевидно, что
Формулы (1) и (2) для нахождения условной вероятности по сути одна и та же формула, это и есть формула Байеса.
Рассмотрим примеры задач на условную вероятность.
Пример 1. На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Результат округлите до сотых.
В задаче описана следующая ситуация: при производстве посуды часть тарелок имеют дефект. Но контроль качества отбраковывает не все дефектные тарелки, а только 80% из них, остальные (20%) поступают в продажу.
Нам нужно найти вероятность того, что что случайно выбранная при покупке тарелка не имеет дефектов. То есть нас интересует какая часть из всех тарелок, которые поступили в продажу, не имеют дефекта.
Нарисуем дерево вероятностей:
Красными веточками обозначены тарелки, которые поступили в продажу. Это тарелки без дефектов (они составляют 0,9 от всех тарелок) и тарелки с дефектами, которые пропустила система контроля. Их 
Таким образом, вероятность того, что тарелка поступила в продажу равна 

Следовательно, вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов равна
40% пакетов с молоком производят на молочном комбинате в Л., а остальные на молокозаводе в С. Известно, что в среднем 3% пакетов, поступивших в продажу протекают, а среди пакетов, изготовленных в Л. протекают в среднем 5%.
а) Найдите вероятность того, что протекающий пакет изготовлен на заводе в С.
б) Найдите вероятность того, что пакет, изготовленный на заводе в С протекает.
Решение. Нам нужно найти вероятность того, что протекающий пакет изготовлен на заводе в С. То есть нам нужно найти, какая часть из всех протекающих пакетов изготовлена на заводе в С. По условию задачи всего протекает 3%, то есть 0,03 часть всех пакетов. Пусть среди пакетов, изготовленных на заводе в С. протекает 
Нарисуем дерево вероятностей:
Красными веточками обозначены пакеты, которые протекают. При этом на заводе в Л. изготовлено 

Получаем 



Тогда вероятность того, что протекающий пакет изготовлен на заводе в С. равна 
Ответ: а) 

Алгебра и начала математического анализа. 11 класс
Конспект урока
Алгебра и начала математического анализа, 11 класс
Урок №34. Условная вероятность. Независимость событий.
Перечень вопросов, рассматриваемых в теме:
— Совместные и несовместные события
— Схема решения задач на вычисление условной вероятности события;
— Задачи на определение независимости событий.
Совместные события – события, одновременное появление которых возможно.
Несовместные события – события, одновременное появление которых невозможно.
События являются независимыми, если вероятность наступления любого из них не зависит от появления остальных событий рассматриваемого множества событий.
Событие В называется зависимым, если вероятность P(B) зависит от появления или непоявления события А. Вероятность события В, вычисленная в предположении того, что событие А уже произошло, называется условной вероятностью наступления события В и обозначается PA(B).
Условная вероятность – вероятность наступления одного события при условии, что другое событие уже произошло.
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014. с. 186-194.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.
Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.
Теоретический материал для самостоятельного изучения
Иногда нам требуется выяснить вероятность совместного появления зависимых событий. Самый простой пример – найти вероятность получить выигрышную комбинацию в азартной карточной игре, где вероятность выпадения каждой новой карты зависит от того, какие карты уже лежат на столе.
Рассмотрим примерную задачу:
Из колоды карт извлекают четыре карты. Первые две оказались семёрками. Какова вероятность, что одна или обе оставшиеся карты окажутся семёрками? (колода содержит 36 карт)
События называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании.
Пример совместных событий: выпадение чётного числа и выпадение числа, кратного трём, при броске игрального кубика. Когда выпадает шесть, реализуются сразу оба события.
События называются несовместными, если появление одного из них исключает появление другого в одном и том же испытании.
Пример несовместных событий: выпадение чётного числа и выпадение нечётного числа при броске игрального кубика.
Теорема о сумме двух событий:
Вероятность суммы любых двух событий А и В равна сумме вероятностей этих событий без вероятности их совместного осуществления: Р(А+В) = Р(А)+Р(В)-Р(АВ)
В лотерее выпущено 10 000 билетов, из них: 10 выигрышей по 200 рублей, 100 выигрышей по 100 рублей, 500 выигрышей по 50 рублей и 1000 выигрышей по 10 рублей. Какова вероятность того, что человек, купивший билет, выиграет не менее 50 рублей?
Воспользуемся теоремой: Р(М)=Р(А)+Р(В)+Р(С)=0,061.
Дана вероятность исходного события. Чему равна вероятность противоположного события?
Вероятность исходного события А обозначим Р(А). Вероятность противоположного события Р(Ᾱ).
События А и Ᾱ образуют полную группу событий, вероятность которой равна 1.
Тогда вероятность противоположного события находится по формуле:
Например, монета брошена два раза.
Вероятность появления «Орла» во втором испытании не зависит от результата первого испытания.
Теорема умножения вероятностей независимых событий: вероятность совместного появления независимых событий A и B равна произведению вероятностей этих событий:
Подбрасываются две монеты. Найдите вероятность выпадения двух орлов.
Введем обозначение событий:
A1– на 1-й монете выпадет орёл;
A2– на 2-й монете выпадет орёл.
Событие “выпадение двух орлов” заключается в том, что на 1-й монете появится орёл и на 2-й монете появится орёл, следовательно, это произведение событий A1A2. Вероятность выпадения орла на одной монете не зависит от результата броска другой монеты, следовательно, события A1 и A2 независимы. По теореме умножения вероятностей независимых событий получим:
Отыскать вероятность совместного появления зависимых событий помогает теорема умножения вероятностей зависимых событий: вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже произошло: P(AB) = P(A)·PA(B).
Связь теории вероятностей с теорией множеств.
В математике принято устанавливать связи между различными разделами. Связь между теорией вероятностей и теорией множеств устанавливается следующим образом: события отождествляются с множествами. В таком случае понятию исход будет эквивалентно понятие элемент множества. При таком подходе выберите из списка, какому понятию из теории множеств соответствует данное понятие из теории вероятностей:
— Невозможное событие (подмножество, бесконечное множество, пустое множество, пересечение множеств, объединение множеств, разность множеств, декартово произведение множеств)
— Сумма событий (подмножество, бесконечное множество, пустое множество, пересечение множеств, объединение множеств, разность множеств, декартово произведение множеств)
— Произведение событий (подмножество, бесконечное множество, пустое множество, пересечение множеств, объединение множеств, разность множеств, декартово произведение множеств)
Примеры и разбор решения заданий тренировочного модуля
1. В урне 6 черных, 5 красных и 4 белых шара. Последовательно извлекают три шара без возврата. Найдите вероятность того, что первый шар окажется черным, второй – красным и третий – белым.
А – первый шар окажется черным

2. Колю отпускают гулять при условии сделанных уроков с вероятностью 0,8. Папа выдает ему деньги на мороженое с вероятностью 0,6. С какой вероятностью Коля пойдет гулять без мороженого?
A – папа выдал Коле денег на мороженое
B – Колю отпустили гулять
Вероятность того, что Коля пойдёт гулять, есть в условии задачи P(B) = 0,8. Вероятность, что папа не выдаст ему деньги на мороженое, равна P(Ᾱ) = 1 – P(A) = 1 – 0,6 = 0,4. Вероятность одновременного осуществления двух независимых событий – произведение их вероятностей P(ᾹB) = P(Ᾱ)·P(B) = 0,8·0,4 = 0,32.
Зависимые события и условная вероятность
На предыдущем уроке мы ознакомились с основными теоремами сложения и умножения вероятностей, а также научились решать типовые задачи с независимыми событиями, и сейчас последует гораздо более интересное продолжение, которое позволит не только освоить новый материал, но и, возможно, окажет практическую житейскую помощь.
Кратко повторим, что такое независимость событий: события 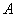
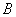
Понятие зависимости событий вам тоже знакомо и настал черёд заняться ими вплотную.
Сначала рассмотрим традиционный набор, состоящий из двух событий: событие 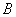
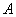
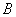
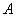
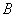
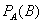
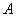
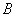
Из колоды в 36 карт последовательно извлекаются 2 карты. Найти вероятность того, что вторая карта окажется червой, если до этого:
а) была извлечена черва;
б) была извлечена карта другой масти.
Решение: рассмотрим событие: 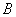
а) Если сначала была извлечена черва (событие 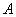
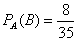
б) Если же сначала была извлечена карта другой масти (событие 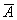
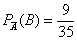
Всё логично – если вероятность извлечения червы из полной колоды составляет 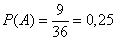
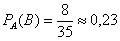
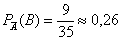
Ответ:
Зависимых событий, разумеется, может быть и больше. Пока задача не остыла, добавим ещё одно: 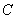
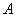
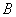
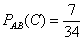
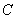
Для самостоятельной тренировки:
В конверте находится 10 лотерейных билетов, среди которых 3 выигрышных. Из конверта последовательно извлекаются билеты. Найти вероятности того, что:
а) 2-й извлечённый билет будет выигрышным, если 1-й был выигрышным;
б) 3-й будет выигрышным, если предыдущие два билета были выигрышными;
в) 4-й будет выигрышным, если предыдущие билеты были выигрышными.
Краткое решение с комментариями в конце урока.
А теперь обратим внимание на один принципиально важный момент: в рассмотренных примерах требовалось найти лишь условные вероятности, при этом предыдущие события считались достоверно состоявшимися. Но ведь в действительности и они являются случайными! Так, в «разогретой» задаче извлечение червы из полной колоды – есть событие случайное, вероятность которого равна 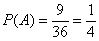
На практике гораздо чаще требуется отыскать вероятность совместного появления зависимых событий. Как, например, найти вероятность события 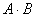
теорема умножения вероятностей зависимых событий: вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже произошло:
В нашем случае:
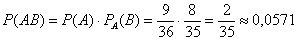
Аналогично:
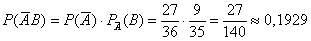
Вероятность события 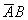
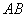
И, само собой, не нужно питать особых надежд, что из конверта с десятью лотерейными билетами (Задача 2) вы вытяните 3 выигрышных билета подряд: 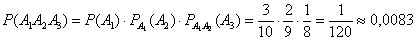
Да, совершенно верно – теорема умножения вероятностей зависимых событий естественным образом распространяется и на бОльшее их количество.
Закрепим материал несколькими типовыми примерами:
В урне 4 белых и 7 черных шаров. Из урны наудачу один за другим извлекают два шара, не возвращая их обратно. Найти вероятность того, что:
а) оба шара будут белыми;
б) оба шара будут чёрными;
в) сначала будет извлечён белый шар, а затем – чёрный.
Обратите внимание на уточнение «не возвращая их обратно». Этот комментарий дополнительно подчёркивает тот факт, что события зависимы. Действительно, а вдруг извлечённые шары возвращают обратно? В случае возвратной выборки вероятности извлечения чёрного и белого шара меняться не будут, а в такой задаче уже следует руководствоваться теоремой умножения вероятностей НЕзависимых событий.
Решение: всего в урне: 4 + 7 = 11 шаров. Поехали:
а) Рассмотрим события 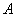
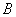
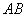
По классическому определению вероятности: 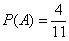
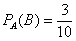
По теореме умножения вероятностей зависимых событий:
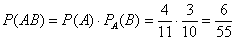
б) Найдём вероятность события 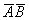
По классическому определению: 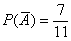
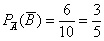
По теореме умножения вероятностей зависимых событий:
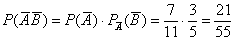
в) Найдём вероятность события 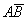
После извлечения белого шара (с вероятностью 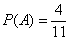
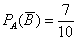
По теореме умножения вероятностей зависимых событий:
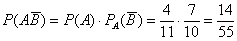
Ответ:
Данную задачу нетрудно проверить через теорему сложения вероятностей событий, образующих полную группу. Для этого найдём вероятность 4-го недостающего события: 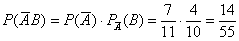
События 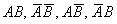
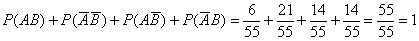
И сразу же предлагаю проверить, насколько хорошо вы усвоили изложенный материал:
Какова вероятность того, что из колоды в 36 карт будут извлечены два туза подряд?
В урне 6 черных, 5 красных и 4 белых шара. Последовательно извлекают три шара. Найти вероятность того, что
а) третий шар окажется белым, если до этого был извлечён черный и красный шар;
б) первый шар окажется черным, второй – красным и третий – белым.
Решения и ответы в конце урока.
Надо сказать, что многие из рассматриваемых задач разрешимы и другим способом, но чтобы не возникло путаницы, пожалуй, вообще о нём умолчу.
Наверное, все заметили, что зависимые события возникают в тех случаях, когда осуществляется некоторая цепочка действий. Однако сама по себе последовательность действий ещё не гарантируют зависимость событий. Пусть, например, студент наугад отвечает на вопросы какого-нибудь теста – данные события хоть и происходят одно за другим, но незнание ответа на один вопрос никак не зависит от незнания других ответов =) Хотя, закономерности тут, конечно, есть =) Тогда совсем простой пример с неоднократным подбрасыванием монеты – сей увлекательный процесс даже так и называется: повторные НЕзависимые испытания.
Я как мог, старался отсрочить этот момент и подбирать разнообразные примеры, но если в задачах на теорему умножения независимых событий хозяйничают стрелки, то здесь происходит самое настоящее нашествие урн с шарами =) Поэтому никуда не деться – снова урна:
Из урны, в которой находится 6 белых и 4 черных шара, извлекаются наудачу один за другим три шара. Найти вероятность того, что:
а) все три шара будут черными;
б) будет не меньше двух шаров черного цвета.
Решение: всего: 6 + 4 = 10 шаров в урне.
Событий в данной задаче будет многовато, и в этой связи целесообразнее использовать смешанный стиль оформления, обозначая прописными латинскими буквами только основные события. Надеюсь, вы уже поняли, по какому принципу подсчитываются условные вероятности.
а) Рассмотрим событие: 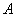
По теореме умножения вероятностей зависимых событий:
б) Второй пункт интереснее, рассмотрим событие: 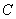
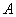
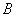
Событие 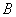
в 1-м испытании извлечён белый и во 2-м и в 3-м испытаниях – чёрные шары
или
в 1-м испытании извлечён ЧШ и во 2-м – БШ и в 3-м – ЧШ
или
в 1-м испытании извлечён ЧШ и во 2-м – ЧШ и в 3-м – БШ.
По теоремам сложения вероятностей несовместных и умножения вероятностей зависимых событий:
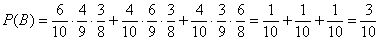
На всякий случай озвучу примерный ход рассуждений при конструировании, например, произведения 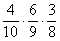
«в 1-м испытании с вероятностью 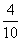
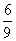
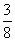
По теореме сложения вероятностей несовместных событий:
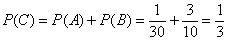
Ответ:
Вы просто не сможете от этого отказаться =):
Из 20 экзаменационных билетов 3 содержат простые вопросы. Пять студентов по очереди берут билеты. Найти вероятность того, что хотя бы одному из них достанется билет с простыми вопросами
А почему бы и нет? Ситуация более чем реалистичная: представьте, начался экзамен, в аудиторию пригласили 5 человек. Проведите самостоятельное исследование – какова вероятность того, что хоть кому-то из этих пяти добровольцев повезёт с билетом?
К вопросу о тактике и стратегии сдачи экзамена мы вернёмся в конце статьи, а пока рассмотрим ещё одну стандартную задачу о перекладывании шаров из урны в урну:
В первой урне содержится 12 шаров, из них 7 белых, во второй – 6 шаров, из них 3 белых. Из первой урны во вторую наудачу перекладывают один шар, а затем из второй урны наудачу извлекают один шар. Найти вероятность того, что он окажется белым.
Решение: по условию, из первой урны во вторую наудачу перекладывают один шар, и, очевидно, он может быть как белым, так и не белым. В этой связи необходимо рассмотреть 2 несовместные гипотезы:
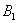
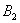
Обозначим через 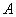
Несовместные исходы удобно расписать по пунктам:
1) По классическому определению: 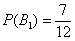
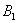
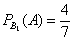
По теореме умножения вероятностей зависимых событий:

2) По классическому определению: 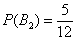
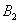
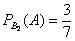
По теореме умножения вероятностей зависимых событий:
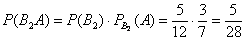
Подводим итог. По теореме сложения вероятностей несовместных событий:
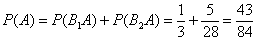
Ответ:
Более интересная вариация по теме:
В первой урне находится 3 белых и 2 черных шара, во второй – 4 белых и 4 черных. Из первой урны во вторую наудачу перекладывают 2 шара. Найти вероятность того, что из второй урны будет извлечён белый шар.
Для решения задания нужно рассмотреть 3 несовместные гипотезы, привлечь на помощь комбинаторику и воспользоваться типовой задачей на классическое определение вероятности.
Желающие могут ознакомиться с более трудными примерами из сборника Чудесенко, в которых перекладываются несколько шаров. Особым любителям предлагаю задачи повышенной комбинационной сложности – с двумя последовательными перемещениями шаров из 1-й во 2-ю урну, из 2-й в 3-ю и финальным извлечением шара из последней урны – смотрите последние задачи файла Дополнительные задачи на теоремы сложения и умножения вероятностей. Кстати, там немало и других интересных заданий.
А в заключение этой статьи мы разберём прелюбопытнейшую задачу, которой я вас заманивал на самом первом уроке =) Даже не разберём, а проведём небольшое практическое исследование. Выкладки в общем виде будут слишком громоздкие, поэтому рассмотрим конкретный пример:
Петя сдаёт экзамен по теории вероятностей, при этом 20 билетов он знает хорошо, а 10 плохо. Предположим, в первый день экзамен сдаёт часть группы, например, 16 человек, включая нашего героя. В общем, ситуация до боли знакома: студенты один за другим заходят в аудиторию и тянут билеты.
Очевидно, что последовательное извлечение билетов представляет собой цепь зависимых событий, и возникает насущный вопрос: в каком случае Пете с бОльшей вероятностью достанется «хороший» билет – если он пойдёт «в первых рядах», или если зайдёт «посерединке», или если будет тянуть билет в числе последних? Когда лучше заходить?
Сначала рассмотрим «экспериментально чистую» ситуацию, в которой Петя сохраняет свои шансы постоянными – он не получает информацию о том, какие вопросы уже достались однокурсникам, ничего не учит в коридоре, ожидая своей очереди, и т.д.
Рассмотрим событие: 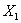
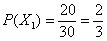
Как изменится вероятность извлечения удачного билета, если пропустить вперёд отличницу Настю? В этом случае возможны две несовместные гипотезы:
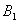
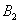
Событие же 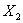
1) Предположим, что Настя с вероятностью 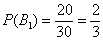
2) Теперь предположим, что Настя с вероятностью 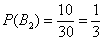
Используя теоремы сложения вероятностей несовместных и умножения вероятностей зависимых событий, вычислим вероятность того, что Петя вытянет «хороший» билет, будучи вторым в очереди:
Вероятность… осталось той же! Хорошо, рассмотрим событие: 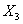
Здесь гипотез будет побольше: дамы могут «обокрасть» джентльмена на 2 удачных билета, либо наоборот – избавить его от 2 неудачных, либо извлечь 1 «хороший» и 1 «плохой» билет. Если провести аналогичные рассуждения, воспользоваться теми же теоремами, то… получится такое же значение вероятности 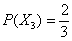
Таким образом, чисто с математической точки зрения, без разницы, когда идти – первоначальные вероятности останутся неизменными. НО. Это только усреднённая теоретическая оценка, так, например, если Петя пойдёт последним, то это вовсе не значит, что ему останутся на выбор 10 «хороших» и 5 «плохих» билетов в соответствии с его изначальными шансами. Данное соотношение может варьироваться в лучшую или худшую сторону, однако всё же маловероятно, что среди билетов останется «одна халява», или наоборот – «сплошной ужас». Хотя «уникальные» случаи не исключены – всё-таки тут не 3 миллиона лотерейных билетов с практически нулевой вероятностью крупного выигрыша. Поэтому «невероятное везение» или «злой рок» будут слишком уж преувеличенными высказываниями. Даже если Петя знает всего лишь 3 билета из 30, то его шансы составляют 10%, что заметно выше нуля. И из личного опыта расскажу обратный случай: на экзамене по аналитической геометрии я хорошо знал 24 вопроса из 28, так вот – в билете мне попались два «плохих» вопроса; вероятность сего события подсчитайте самостоятельно 🙂
Математика и «чистый эксперимент» – это хорошо, но какой стратегии и тактики всё же выгоднее придерживаться в реальных условиях? Безусловно, следует принять во внимание субъективные факторы, например, «скидку» преподавателя для «храбрецов» или его усталость к концу экзамена. Зачастую эти факторы могут быть даже решающими, но в заключительных рассуждениях я постараюсь не сбрасывать со счетов и дополнительные вероятностные аспекты:
Если Вы готовы к экзамену хорошо, то, наверное, лучше идти «в первых рядах». Пока билетов полный комплект, постулат «маловозможные события не происходят» работает на Вас гораздо в бОльшей степени. Согласитесь, что намного приятнее иметь соотношение «30 билетов, среди которых 2 плохих», чем «15 билетов, среди которых 2 плохих». А то, что два неудачных билета на отдельно взятом экзамене (а не по средней теоретической оценке!) так и останутся на столе – вполне и вполне возможно.
Теперь рассмотрим «ситуацию Пети» – когда студент готов к экзамену достаточно хорошо, но с другой стороны, и «плавает» тоже неплохо. Иными словам, «больше знает, чем не знает». В этом случае целесообразно пропустить вперёд 5-6 человек, и ожидать подходящего момента вне аудитории. Действуйте по ситуации. Довольно скоро начнёт поступать информация, какие билеты вытянули однокурсники (снова зависимые события!), и на «заигранные» вопросы можно больше не тратить силы – учите и повторяйте другие билеты, повышая тем самым первоначальную вероятность своего успеха. Если «первая партия» экзаменующихся «избавила» вас сразу от 3-4 трудных (лично для Вас) билетов, то выгоднее как можно быстрее попасть на экзамен – именно сейчас шансы значительно возросли. Постарайтесь не упускать момент – всего несколько пропущенных вперёд человек, и преимущество, скорее всего, растает. Если же наоборот, «плохих» билетов вытянули мало – ждите. Через несколько человек эта «аномалия» опять же с большой вероятностью, если не исчезнет, то сгладится в лучшую сторону. В «обычном» и самом распространённом случае выгода тоже есть: расклад «24 билета/8 плохих» будет лучше соотношения «30 билетов/10 плохих». Почему? Трудных билетов теперь не десять, а восемь! С удвоенной энергией штудируем материал!
Если Вы готовы неважно или плохо, то само собой, лучше идти в «последних рядах» (хотя возможны и оригинальные решения, особенно, если нечего терять). Существует небольшая, но всё же ненулевая вероятность, что Вам останутся относительно простые вопросы + дополнительная зубрёжка + шпоры, которые отдадут отстрелявшиеся сокурсники =) И, да – в совсем критической ситуации есть ещё следующий день, когда экзамен сдаёт вторая часть группы 😉
Какой можно сделать вывод? Субъективный оценочный принцип «кто идёт раньше, тот готов лучше» находит внятное вероятностное обоснование!
Ну, а если на экзамене произойдёт «несчастный случай», не расстраивайтесь и вспомните моё пожелание:
Задача 2: Решение: рассмотрим события: 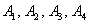
а) Пусть событие 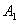
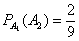
б) Если произошли события 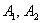
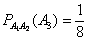
в) Если произошли события 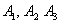
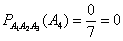
Ответ:
Задача 4: Решение: всего: 4 туза в колоде. Рассмотрим события 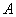
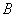
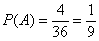
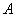
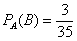
По теореме умножения вероятностей зависимых событий:
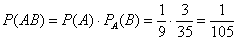
Ответ:
Задача 5: Решение: всего: 6 + 5 + 4 = 15 шаров в урне. Рассмотрим следующие события:
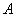
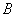
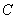
а) По условию, события 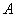
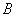
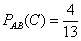
б) По классическому определению: 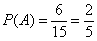
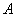
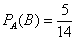
По теореме умножения вероятностей зависимых событий:
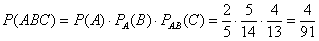
Ответ:
Задача 7: Решение: рассмотрим события:
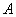
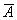
Данные события являются противоположными, поэтому 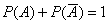
По теореме умножения вероятностей зависимых событий: 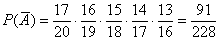
Таким образом: 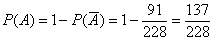
Ответ:
Задача 9: Решение: рассмотрим зависимое событие 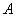
1) 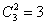
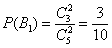
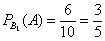
2) 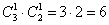
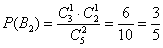
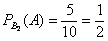
3) 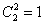
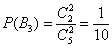
По теоремам сложения вероятностей несовместных и умножения вероятностей зависимых событий:

– вероятность того, что из второй урны будет извлечен белый шар.
Ответ: