что такое условная гибкость

Что такое жесткость и гибкость элементов

Разницу в работе гибких и жестких стержней под воздействием нагрузки люди заметили достаточно давно. Так один из мастеров восточных единоборств, гуляя по зимнему саду, сделал примерно следующий вывод: жесткая сухая ветка под тяжестью налипшего снега ломается, а гибкая ветка прогибается и, сбросив налипший снег, возвращается в прежнее положение с минимумом повреждений.

Если перевести это гибкую поэтическую аллегорию, помогавшую мастеру восточных единоборств привлекать новых учеников, на современный жесткий язык теории сопротивления материалов, то звучать это будет примерно так: если напряжения в рассматриваемом поперечном сечении жесткого элемента конструкции превышают значение нормативного сопротивления, то это приведет сначала к значительным пластическим деформациям, а затем, при увеличении напряжений, и к разрушению жесткого элемента (будет это разрушение хрупким или вязким, принципиального значения не имеет). В то же время гибкий элемент конструкции под действием такой же нагрузки, не разрушится, но потеряет устойчивость.

Конечно же мне, как и любому другому обычному человеку, гораздо ближе и понятнее определение жесткости и гибкости, данное средневековым мастером восточных единоборств. Но справедливости ради следует отметить, что этот мастер сильно перегнул палку (точнее ветку или, выражаясь языком строительной механики, стержень). Дело в том, что гибкий стержень потеряет устойчивость задолго до того, как значение нагрузки в переводе на напряжения в рассматриваемом сечении достигнет уровня нормативного сопротивления.

Чтобы было более понятно, о чем идет речь, приведу еще один пример.

Если взять достаточно ровный человеческий волос со среднестатистического человека длиной 10 см и попробовать его разорвать руками, то это будет не так уж и просто, для этого следует приложить достаточно большую физическую силу, или выражаясь по-научному, создать достаточно большие растягивающие напряжения в волосе или растягивающую силу около 5 кг (может больше, может меньше, не в этом суть).

А вот если мы попробуем поставить этот волос в вертикальное положение, например, на стол, то волос стоять не будет, а будет сгибаться под действием своего собственного веса, вряд ли превышающего несколько миллиграмм, даже если мы обеспечим ему такое закрепление на верхней опоре, при котором верх волоса не сможет смещаться в горизонтальном направлении, но сможет смещаться в вертикальном направлении.

Вот такое, условно говоря, сгибание и означает потерю устойчивости. Таким образом использовать очень гибкие стержни в качестве сжатых элементов строительных конструкций не имеет никакого смысла.

Между тем, если мы отрежем от этого же волоса кусок длиной 1 см, то этот кусок уже будет сгибаться не так сильно под действием собственного веса и будет обладать некоторой устойчивостью, а если это будет волос длиной 2-5 мм, то об него уже можно сильно уколоться, а волос при этом даже и не согнется.

Как, надеюсь, понятно из вышеприведенного примера, даже для стержня с постоянными геометрическими характеристиками поперечного сечения (радиусом инерции и моментом инерции) его устойчивость зависит от расчетной длины стержня. Другими словами один и тот же стержень может быть и гибким и жестким в зависимости от его расчетной длины.

Для того, чтобы определить гибкость элемента, достаточно расчетную длину элемента l_o разделить на радиус инерции i поперечного сечения (при условии, что параметры поперечных сечений постоянны по всей длине элемента):

Примечание: в различных нормативных документах указанные характеристики могут иметь и другие обозначения, но принципиального значения это не имеет.

Таким образом чем меньше гибкость элемента, тем он более жесткий, соответственно чем больше гибкость элемента, тем более он гибкий. А чтобы определить, не является ли такая гибкость чрезмерной для рассматриваемого элемента конструкции, используются таблицы из соответствующих нормативных документов.

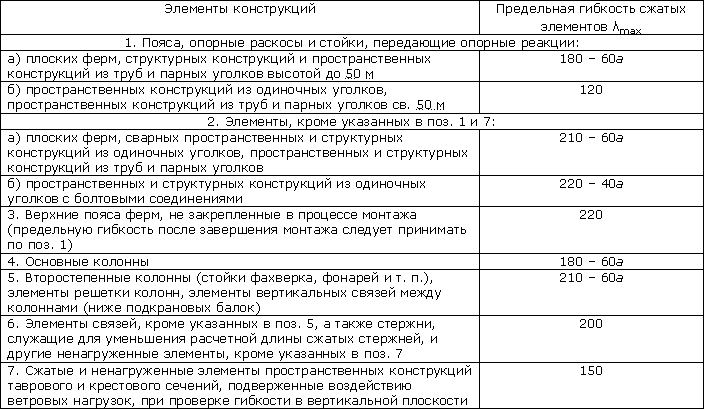
Например, при расчете сжатых элементов стальных конструкций используется такая таблица:

Таблица 19* (согласно СНиП II-23-81 (1990))

А при расчете деревянных конструкций, такая:

Таблица 251.1. Предельные значения гибкости (согласно СНиП II-25-80 (1988))

На значение гибкости влияет и модуль упругости материала. Чем меньше значение модуля упругости, тем больше может быть гибкость. В связи с этим предельно допустимые значения гибкости могут быть разные для элементов из различных материалов, что и отражено в указанных таблицах.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).

Источник

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Устойчивость сжатых стержней

Продольный изгиб

При расчетах на прочность подразумевалось, что равновесие конструкции под действием внешних сил является устойчивым. Однако выход конструкции из строя может произойти из-за того, что равновесие конструкций в силу тех или иных причин окажется неустойчивым. Во многих случаях, кроме проверки прочности, необходимо производить еще проверку устойчивости элементов конструкций.

Состояние равновесия считается устойчивым, если при любом возможном отклонении системы от положения равновесия возникают силы, стремящиеся вернуть её в первоначальное положение.

Рассмотрим известные виды равновесия.

Неустойчивое равновесное состояние будет в том случае, когда хотя бы при одном из возможных отклонений системы от положения равновесия возникнут силы, стремящиеся удалить её от начального положения.

Состояние равновесия будет безразличным, если при разных отклонениях системы от положения равновесия возникают силы, стремящиеся вернуть её в начальное положение, но хотя бы при одном из возможных отклонений система продолжает оставаться в равновесии при отсутствии сил, стремящихся вернуть её в начальное положение или удалить от этого положения.

При потере устойчивости характер работы конструкции меняется, так как этот вид деформации переходит в другой, более опасный, способный привести её к разрушению при нагрузке значительно меньшей, чем это следовало из расчета на прочность. Очень существенно, что потеря устойчивости сопровождается нарастанием больших деформаций, поэтому явление это носит характер катастрофичности.

При переходе от устойчивого равновесного состояния к неустойчивому конструкция проходит через состояние безразличного равновесия. Если находящейся в этом состоянии конструкции сообщить некоторое небольшое отклонение от начального положения, то по прекращении действия причины, вызвавшей это отклонение, конструкция в исходное положение уже не вернется, но будет способна сохранить приданное ей, благодаря отклонению, новое положение.

Состояние безразличного равновесия, представляющее как бы границу между двумя основными состояниями – устойчивым и неустойчивым, называется критическим состоянием. Нагрузка, при которой конструкция сохраняет состояние безразличного равновесия, называется критической нагрузкой.

Эксперименты показывают, что обычно достаточно немного увеличить нагрузку по сравнению с её критическим значением, чтобы конструкция из-за больших деформаций потеряла свою несущую способность, вышла из строя. В строительной технике потеря устойчивости даже одним элементом конструкции вызывает перераспределение усилий во всей конструкции и нередко влечет к аварии.

Изгиб стержня,связанный с потерей устойчивости, называется продольным изгибом.

Критическая сила. Критическое напряжение

Наименьшая величина сжимающей силы, при которой первоначальная форма равновесия стержня – прямолинейная становится неустойчивой – искривленной, называется критической.

При исследовании устойчивости форм равновесия упругих систем первые шаги были сделаны Эйлером.

В упругой стадии деформирования стержня при напряжениях, не превышающих предел пропорциональности, критическая сила вычисляется по формуле Эйлера:

Критическое напряжение вычисляется следующим образом

а радиус инерции сечения.

Введем понятие предельной гибкости.

Величина λ_пред зависит только от вида материала:

Если у стали 3 Е=2∙10 11 Па, а σ_пц=200МПа, то предельная гибкость

Для дерева (сосна, ель) предельная гибкость λпред=70, для чугуна λпред=80

Таким образом, для стержней большой гибкости λ≥λ_пред критическая сила определяется по формуле Эйлера.

В упругопластической стадии деформирования стержня, когда значение гибкости находится в диапазоне λ₀≤λ≤λ_пр, (стержни средней гибкости) расчет проводится по эмпирическим формулам, например, можно использовать формулу Ясинского Ф.С. Значения введенных в нее параметров определены эмпирически для каждого материала.

где a и b – постоянные, определяемые экспериментальным путем (эмпирические коэффициенты).Так, для стали3 а=310МПа, b=1,14МПа.

При значениях гибкости стержня 0≤λ≤λ₀ (стержни малой гибкости) потеря устойчивости не наблюдается.

Таким образом, пределы применимости формулы Эйлера — применяется только в зоне упругих деформаций.

Условие устойчивости. Типы задач при расчете на устойчивость. Коэффициент продольного изгиба

Условием устойчивости сжатого стержня является неравенство:

Здесь допускаемое напряжение по устойчивости [σуст] — не постоянная величина, как это было в условиях прочности, а зависящая от следующих факторов:

1) от длины стержня, от размеров и даже от формы поперечных сечений,

2) от способа закрепления концов стержня,

3) от материала стержня.

Как и всякая допускаемая величина, [σуст] определяется отношением опасного для сжатого стержня напряжения к коэффициенту запаса. Для сжатого стержня опасным является так называемое критическое напряжение σкр, при котором стержень теряет устойчивость первоначальной формы равновесия.

Величину коэффициента запаса в задачах устойчивости принимают несколько большей, чем значение коэффициента запаса прочности, то есть если k=1÷2, то kуст=2÷5.

Допускаемое напряжение по устойчивости можно связать с допускаемым напряжением по прочности:

где σт – опасное с точки зрения прочности напряжение (для пластичных материалов это предел текучести, а для хрупких – предел прочности на сжатие σвс).

Коэффициент φ Запись опубликована 24.09.2014 автором admin в рубрике Устойчивость.

Источник

6. Расчетные длины и предельные гибкости элементов стальных конструкций

6.5*. Расчетные длины lef и радиусы инерции сечений i сжатых и ненагруженных элементов из одиночных уголков при определении гибкости следует принимать по табл. 13*.

Обозначения, принятые в табл. 13* (рис. 9*):

1. Раскосы по рис. 9*, а, д, е в точках пересечения должны быть скреплены между собой.

2. Для раскосов по рис. 9*, е необходима дополнительная проверка их из плоскости грани с учетом расчета по деформированной схеме.

3. Значение lef для распорок по рис 9*, в дано для равнополочных уголков.

Расчетные длины lef и радиусы инерции i растянутых элементов из одиночных уголков при определении гибкости следует принимать:

для перекрестных раскосов по рис. 9*, а, д, е:

Расчетные длины lef и радиус инерции i элементов из труб или парных уголков следует принимать согласно требованиям подраздела «Расчетные длины элементов плоских ферм и связей».

Расчетные длины элементов структурных конструкций

6.7. Расчетные длины lef элементов структурных конструкций следует принимать по табл. 17.

Радиусы инерции сечений i элементов структурных конструкций при определении гибкости следует принимать:

для сжато-изгибаемых элементов относительно оси, перпендикулярной или параллельной плоскости изгиба (i = ix или i = iy);

Расчетные длины колонн (стоек)

6.8. Расчетные длины lef колонн (стоек) постоянного сечения или отдельных участков ступенчатых колонн следует определять по формуле

6.9*. Коэффициенты расчетной длины M колонн и стоек постоянного сечения следует принимать в зависимости от условий закрепления их концов и вида нагрузки.

Для некоторых случаев закрепления и вида нагрузки значения M приведены в прил. 6, табл. 71, а.

6.10*. Коэффициенты расчетной длины колонн постоянного сечения в плоскости рамы при жестком креплении ригелей к колоннам следует определять:

для свободных рам при одинаковом нагружении верхних узлов по формулам табл. 17, а;

Элементы структурных конструкций

Расчетная длина l_ef

1. Кроме указанных в поз. 2 и 3

2. Неразрезные (не прерывающиеся в узлах) пояса и прикрепляемые в узлах сваркой впритык к шаровым или цилиндрическим узловым элементам

3. Из одиночных уголков, прикрепляемых в узлах одной полкой:

а) сварными швами или болтами (не менее двух),расположенными вдоль элемента, при l / i_min:

« 120 « 150 (только для элементов решетки)

св. 150 до 200 (только для элементов решетки)

б) одним болтом при l / i_min:

« 120 « 150 (только для элементов решетки)

св. 150 до 200 (только для элементов решетки)

Обозначение, принятое в табл. 17:

6.11*. Коэффициенты расчетной длины M отдельных участков ступенчатых колонн в плоскости рамы следует определять согласно прил. 6.

При определении коэффициентов расчетной длины M для ступенчатых колонн рам одноэтажных производственных зданий разрешается:

не учитывать влияние степени загружения и жесткости соседних колонн;

определять расчетные длины колонн лишь для комбинации нагрузок, дающей наибольшие значения продольных сил на отдельных участках колонн, и получаемые значения M использовать для других комбинаций нагрузок;

для многопролетных рам (с числом пролетов два и более) при наличии жесткого диска покрытия или продольных связей, связывающих поверху все колонны и обеспечивающих пространственную работу сооружения, определять расчетные длины колонн как для стоек, неподвижно закрепленных на уровне ригелей;

для одноступенчатых колонн при соблюдении условий l2/l1 M 0,6 и N1/N2 M 3 принимать значения M по табл. 18.

6.13. Расчетные длины колонн в направлении вдоль здания (из плоскости рам) следует принимать равными расстояниям между закрепленными от смещения из плоскости рамы точками (опорами колонн, подкрановых балок и подстропильных ферм; узлами креплений связей и ригелей и т.п.). Расчетные длины допускается определять на основе расчетной схемы, учитывающей фактические условия закрепления концов колонн.

Источник