что такое уровень значимости
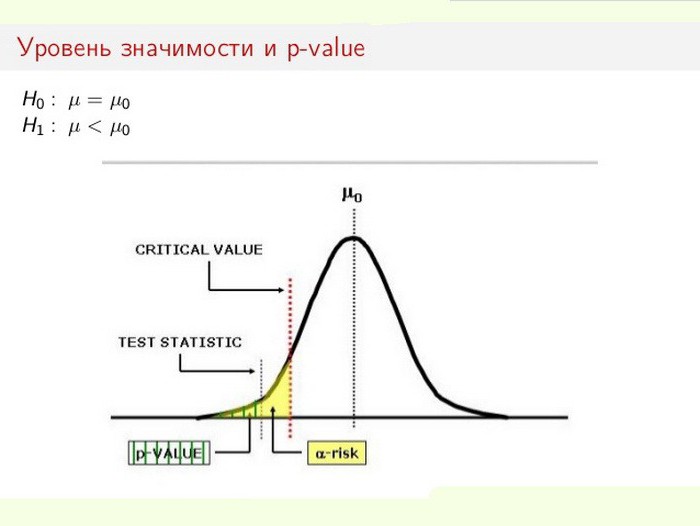
4. Уровень значимости
Уровни статистической значимости
Уровень значимости – это вероятность того, что мы сочли различия существенными, в то время как они на самом деле случайны.
Итак, уровень значимости имеет дело с вероятностью.
Уровень значимости показывает степень достоверности выявленных различий между выборками, т.е. показывает, насколько мы можем доверять тому, что различия действительно есть.
Современные научные исследования требуют обязательных расчётов уровня статистической значимости результатов.
Обычно в прикладной статистике используют 3 уровня значимости.
Это 5%-ный уровень значимости. До 5% составляет вероятность того, что мы ошибочно сделали вывод о том, что различия достоверны, в то время как они недостоверны на самом деле. Можно сказать и по-другому: мы лишь на 95% уверены в том, что различия действительно достоверны. В данном случае можно написать и так: P> 0,95. Общий смысл критерия останется тем же.
Это 1%-ный уровень значимости. Вероятность ошибочного вывода о том, что различия достоверны, составляет не более 1%. Можно сказать и по-другому: мы на 99% уверены в том, что различия действительно достоверны. В данном случае можно написать и так: P> 0,99. Смысл останется тем же.
Это 0,1%-ный уровень значимости. Всего 0,1% составляет вероятность того, что мы сделали ошибочный вывод о том, что различия достоверны. Это — самый надёжный вариант вывода о достоверности различий. Можно сказать и по-другому: мы на 99,9% уверены в том, что различия действительно достоверны. В данном случае можно написать и так: P> 0,999. Смысл опять-таки останется тем же.
Уровень значимости – это допустимая ошибка в нашем утверждении, в нашем выводе.
Возможны ошибки двух родов: первого рода ( α ) и второго рода ( β ).
Ошибка I рода – мы отклонили нулевую гипотезу, в то время как она верна.
Вероятность того, что принято правильное решение: 1 – α = 0,95, или 95%.
Уровни значимости для ошибок I рода
1. α ≤ 0,05 – низший уровень
Низший уровень значимости – позволяет отклонять нулевую гипотезу, но еще не разрешает принять альтернативную.
2. α ≤ 0,01 – достаточный уровень
Достаточный уровень – позволяет отклонять нулевую гипотезу и принимать альтернативную.
G – критерий знаков
T – критерий Вилкоксона
U – критерий Манна – Уитни.
Для них обратное соотношение.
3. α ≤ 0,001 – высший уровень значимости.
На практике различия считают достоверными при р ≤ 0,05.
Для ненаправленной статистической гипотезы используется двусторонний критерий значимости. Он более строгий, так как проверяет различия в обе стороны: в сторону нулевой гипотезы и в сторону альтернативной. Поэтому для него используется критерий значимости 0,01.
Мощность критерия – его способность выявлять даже мелкие различия если они есть. Чем мощнее критерий, тем лучше он отвергает нулевую гипотезу и подтверждает альтернативную.
Здесь появляется понятие: ошибка II рода.
Ошибка II рода – это принятие нулевой гипотезы, хотя она не верна.
Мощность критерия: 1 – β
Чем мощнее критерий, тем он привлекательнее для исследователя. Он лучше отвергает нулевую гипотезу.
Чем привлекательны маломощные критерии?
Достоинства маломощных критериев
Широкий диапазон, по отношению к самым разным данным
Применимость к неравным по объему выборкам.
Большая информативность результатов.
Второй по популярности — критерий хи-квадрат, χ 2
Т-критерий Стьюдента – это частный случай дисперсионного анализа для более маленькой по объёму выборки.
Уровень статистической значимости (р)
В таблицах результатов статистических расчётов в курсовых, дипломных и магистерских работах по психологии всегда присутствует показатель «р».
Например, в соответствии с задачами исследования были рассчитаны различия уровня осмысленности жизни у мальчиков и девочек подросткового возраста.
Уровень статистической значимости (p)
В правом столбце указано значение «р» и именно по его величине можно определить значимы различия осмысленности жизни в будущем у мальчиков и девочек или не значимы. Правило простое:
Откуда берется уровень статистической значимости «р»
Уровень статистической значимости вычисляется статистической программой вместе с расчётом статистического критерия. В этих программах можно также задать критическую границу уровня статистической значимости и соответствующие показатели будут выделяться программой.
Например, в программе STATISTICA при расчете корреляций можно установить границу «р», например, 0,05 и все статистически значимые взаимосвязи будут выделены красным цветом.
Если расчёт статистического критерия проводится вручную, то уровень значимости «р» выявляется путем сравнения значения полученного критерия с критическим значением.
Что показывает уровень статистической значимости «р»
Все статистические расчеты носят приблизительный характер. Уровень этой приблизительности и определяет «р». Уровень значимости записывается в виде десятичных дробей, например, 0,023 или 0,965. Если умножить такое число на 100, то получим показатель р в процентах: 2,3% и 96,5%. Эти проценты отражают вероятность ошибочности нашего предположения о взаимосвязи, например, между агрессивностью и тревожностью.
То есть, коэффициент корреляции 0,58 между агрессивностью и тревожностью получен при уровне статистической значимости 0,05 или вероятности ошибки 5%. Что это конкретно означает?
Выявленная нами корреляция означает, что в нашей выборке наблюдается такая закономерность: чем выше агрессивность, тем выше тревожность. То есть, если мы возьмем двух подростков, и у одного тревожность будет выше, чем у другого, то, зная о положительной корреляции, мы можем утверждать, что у этого подростка и агрессивность будет выше. Но так как в статистике все приблизительно, то, утверждая это, мы допускаем, что можем ошибиться, причем вероятность ошибки 5%. То есть, сделав 20 таких сравнений в этой группе подростков, мы можем 1 раз ошибиться с прогнозом об уровне агрессивности, зная тревожность.
Какой уровень статистической значимости лучше: 0,01 или 0,05
Уровень статистической значимости отражает вероятность ошибки. Следовательно, результат при р=0,01 более точный, чем при р=0,05.
В психологических исследованиях приняты два допустимых уровня статистической значимости результатов:
р=0,01 – высокая достоверность результата сравнительного анализа или анализа взаимосвязей;
р=0,05 – достаточная точность.
Надеюсь, эта статья поможет вам написать работу по психологии самостоятельно. Если понадобится помощь, обращайтесь (все виды работ по психологии; статистические расчеты). Заказать
Уровень значимости в статистике
Уровень значимости в статистике является важным показателем, отражающим степень уверенности в точности, истинности полученных (прогнозируемых) данных. Понятие широко применяется в различных сферах: от проведения социологических исследований, до статистического тестирования научных гипотез.
Определение
Уровень статистической значимости (или статистически значимый результат) показывает, какова вероятность случайного возникновения исследуемых показателей. Общая статистическая значимость явления выражается коэффициентом р-value (p-уровень). В любом эксперименте или наблюдении существует вероятность, что полученные данные возникли из-за ошибок выборки. Особенно это актуально для социологии.
То есть статистически значимой является величина, чья вероятность случайного возникновения крайне мала либо стремится к крайности. Крайностью в этом контексте считают степень отклонения статистики от нуль-гипотезы (гипотезы, которую проверяют на согласованность с полученными выборочными данными). В научной практике уровень значимости выбирается перед сбором данных и, как правило, его коэффициент составляет 0,05 (5 %). Для систем, где крайне важны точные значения, этот показатель может составлять 0,01 (1 %) и менее.
История вопроса
Понятие уровня значимости было введено британским статистиком и генетиком Рональдом Фишером в 1925 году, когда он разрабатывал методику проверки статистических гипотез. При анализе какого-либо процесса существует определенная вероятность тех либо иных явлений. Трудности возникают при работе с небольшими (либо не очевидными) процентами вероятностей, подпадающими под понятие «погрешность измерений».
При работе со статистическими данными, недостаточно конкретными, чтобы их проверить, ученые сталкивались с проблемой нулевой гипотезы, которая «мешает» оперировать малыми величинами. Фишер предложил для таких систем определить вероятность событий в 5 % (0,05) в качестве удобного выборочного среза, позволяющего отклонить нуль-гипотезу при расчетах.
Введение фиксированного коэффициента
В 1933 году ученые Ежи Нейман и Эгон Пирсон в своих работах рекомендовали заранее (до сбора данных) устанавливать определенный уровень значимости. Примеры использования этих правил хорошо видны во время проведения выборов. Предположим, есть два кандидата, один из которых очень популярен, а второй – малоизвестен. Очевидно, что первый кандидат выборы выиграет, а шансы второго стремятся к нулю. Стремятся – но не равны: всегда есть вероятность форс-мажорных обстоятельств, сенсационной информации, неожиданных решений, которые могут изменить прогнозируемые результаты выборов.
Нейман и Пирсон согласились, что предложенный Фишером уровень значимости 0,05 (обозначаемый символом α) наиболее удобен. Однако сам Фишер в 1956 году выступил против фиксации этого значения. Он считал, что уровень α должен устанавливаться в соответствии с конкретными обстоятельствами. Например, в физике частиц он составляет 0,01.
Значение p-уровня
Термин р-value впервые использован в работах Браунли в 1960 году. P-уровень (p-значение) является показателем, находящимся в обратной зависимости от истинности результатов. Наивысший коэффициент р-value соответствует наименьшему уровню доверия к произведенной выборке зависимости между переменными.
Данное значение отражает вероятность ошибок, связанных с интерпретацией результатов. Предположим, p-уровень = 0,05 (1/20). Он показывает пятипроцентную вероятность того, что найденная в выборке связь между переменными – всего лишь случайная особенность проведенной выборки. То есть, если эта зависимость отсутствует, то при многократных подобных экспериментах в среднем в каждом двадцатом исследовании можно ожидать такую же либо большую зависимость между переменными. Часто p-уровень рассматривается в качестве «допустимой границы» уровня ошибок.
Кстати, р-value может не отражать реальную зависимость между переменными, а лишь показывает некое среднее значение в пределах допущений. В частности, окончательный анализ данных будет также зависеть от выбранных значений данного коэффициента. При p-уровне = 0,05 будут одни результаты, а при коэффициенте, равном 0,01, другие.
Проверка статистических гипотез
Уровень статистической значимости особенно важен при проверке выдвигаемых гипотез. Например, при расчетах двустороннего теста область отторжения разделяют поровну на обоих концах выборочного распределения (относительно нулевой координаты) и высчитывают истинность полученных данных.
Предположим, при мониторинге некоего процесса (явления) выяснилось, что новая статистическая информация свидетельствует о небольших изменениях относительно предыдущих значений. При этом расхождения в результатах малы, не очевидны, но важны для исследования. Перед специалистом встает дилемма: изменения реально происходят или это ошибки выборки (неточность измерений)?
Эффективность
Необходимо учитывать, что коэффициенты α и р-value не являются точными характеристиками. Каким бы ни был уровень значимости в статистике исследуемого явления, он не является безусловным основанием для принятия гипотезы. Например, чем меньше значение α, тем больше шанс, что устанавливаемая гипотеза значима. Однако существует риск ошибиться, что уменьшает статистическую мощность (значимость) исследования.
Исследователи, которые зацикливаются исключительно на статистически значимых результатах, могут получить ошибочные выводы. При этом перепроверить их работу затруднительно, так как ими применяются допущения (коими фактически и являются значения α и р-value). Поэтому рекомендуется всегда, наряду с вычислением статистической значимости, определять другой показатель – величину статистического эффекта. Величина эффекта – это количественная мера силы эффекта.
Проверка статистических гипотез
п.1. Понятие о статистической гипотезе
В результате проверки гипотезы возможны 4 исхода:
| Верная гипотеза | |||
| \(H_0\) | \(H_1\) | ||
| Принятая гипотеза | \(H_0\) | True Negative \(H_0\) принята верно | False Negative \(H_0\) принята неверно Ошибка 2-го рода |
| \(H_1\) | False Positive \(H_0\) отвергнута неверно \(H_1\) принята неверно Ошибка 1-го рода | True Positive \(H_0\) отвергнута верно \(H_1\) принята верно | |
Ошибка 1-го рода – «ложная тревога».
Ошибка 2-го рода – «пропуск события».
Уровень значимости при проверке гипотезы
Например:
Уровень значимости α=0,05 означает, что допускается не более чем 5%-ая вероятность ошибки.
Обобщив практический опыт, можно сформулировать следующие рекомендации для оценки p и выбора критического значения α:
| Уровень значимости \(p\) | Решение о гипотезе \(H_0\) | Вывод для гипотезы \(H_1\) |
| \(p\gt 0,1\) | \(H_0\) не может быть отклонена | Статистически достоверные доказательства не обнаружены |
| \(0,5\lt p\leq 0,1\) | Истинность \(H_0\) сомнительна, неопределенность | Доказательства обнаружены на уровне статистической тенденции |
| \(0,01\lt p\leq 0,05\) | Отклонение \(H_0\), значимость | Обнаружены статистически достоверные (значимые) доказательства |
| \(p\leq 0,01\) | Отклонение \(H_0\), высокая значимость | Доказательства обнаружены на высоком уровне значимости |
Здесь под «доказательствами» мы понимаем результаты наблюдений, свидетельствующие в пользу гипотезы \(H_1\).
Традиционно уровень значимости α=0,05 выбирается для небольших выборок, в которых велика вероятность ошибки 2-го рода. Для выборок с \(n\geq 100\) критический уровень снижают до α=0,01.
п.3. Критическая область
Различают 3 вида критических областей
п.4. Простая гипотеза и критерии согласия
Например:
Глядя на полученные данные эксперимента (синие точки), можно выдвинуть следующую простую гипотезу:
\(H_0\): данные являются выборкой из равномерного распределения на отрезке [-1;1]
Критерий согласия проверяет, согласуется ли заданная выборка с заданным распределением или с другой выборкой.
п.5. Критерий согласия \(X^2\) Пирсона
Например:
В эксперименте 60 раз подбрасывают игральный кубик и получают следующие результаты:
Не является ли кубик фальшивым?
| \(x_i\) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| \(f_i\) | 8 | 12 | 13 | 7 | 12 | 8 | 60 |
| \(m_i\) | 10 | 10 | 10 | 10 | 10 | 10 | 60 |
| \(f_i-m_i\) | -2 | 2 | 3 | -3 | 2 | -2 | — |
| \(\frac<(f_i-m_i)^2> | 0,4 | 0,4 | 0,9 | 0,9 | 0,4 | 0,4 | 3,4 |
п.6. Примеры
Пример 1. В эксперименте 72 раза подбрасывают игральный кубик и получают следующие результаты:
Не является ли кубик фальшивым?
| \(x_i\) | 1 | 2 | 3 | 4 | 5 | 6 | ∑ |
| \(f_i\) | 8 | 12 | 13 | 7 | 10 | 22 | 72 |
| \(m_i\) | 12 | 12 | 12 | 12 | 12 | 12 | 72 |
| \(f_i-m_i\) | -4 | 0 | 1 | -5 | -2 | 10 | — |
| \(\frac<(f_i-m_i)^2> | 1,333 | 0,000 | 0,083 | 2,083 | 0,333 | 8,333 | 12,167 |
Пример 2. Во время Второй мировой войны Лондон подвергался частым бомбардировкам. Чтобы улучшить организацию обороны, город разделили на 576 прямоугольных участков, 24 ряда по 24 прямоугольника.
В течение некоторого времени были получены следующие данные по количеству попаданий на участки:
| Число попаданий, \(x_i\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Количество участков, \(f_i\) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 |
| \(x_i\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| \(f_i\) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| \(x_if_i\) | 0 | 211 | 186 | 105 | 28 | 0 | 0 | 7 | 537 |
| \(x_i\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ∑ |
| \(f_i\) | 229 | 211 | 93 | 35 | 7 | 0 | 0 | 1 | 576 |
| \(p_i\) | 0,39365 | 0,36700 | 0,17107 | 0,05316 | 0,01239 | 0,00231 | 0,00036 | 0,00005 | 0,99999 |
| \(m_i\) | 226,7 | 211,4 | 98,5 | 30,6 | 7,1 | 1,3 | 0,2 | 0,0 | 576,0 |
| \(f_i-m_i\) | 2,3 | -0,4 | -5,5 | 4,4 | -0,1 | -1,3 | -0,2 | 1,0 | — |
| \(\frac<(f_i-m_i)^2> | 0,02 | 0,00 | 0,31 | 0,63 | 0,00 | 1,33 | 0,21 | 34,34 | 36,84 |
Значение теста: \(X_e^2=36,84\)
Поскольку в ходе исследования мы нашли оценку для λ через подсчет выборочной средней, нужно уменьшить число степеней свободы на r=1, и критическое значение статистики искать для \(X_<кр>^2=X^2(\alpha,k-2)\).
Для уровня значимости α=0,05 и k=8, r=1 находим:
\(X_<кр>^2\approx 12,59\)
Получается, что: \(X_e^2\gt X_<кр>^2\)
Гипотеза \(H_0\) не принимается.
Стрельба не случайна.
Пример 3. В предыдущем примере объединили события x= <4;5;6;7>с редким числом попаданий:
| Число попаданий, \(x_i\) | 0 | 1 | 2 | 3 | 4-7 |
| Количество участков, \(f_i\) | 229 | 211 | 93 | 35 | 8 |
| \(x_i\) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| \(f_i\) | 229 | 211 | 93 | 35 | 8 | 576 |
| \(x_if_i\) | 0 | 211 | 186 | 105 | 35 | 537 |
| \(x_i\) | 0 | 1 | 2 | 3 | 4,375 | ∑ |
| \(f_i\) | 229 | 211 | 93 | 35 | 8 | 576 |
| \(p_i\) | 0,3937 | 0,3670 | 0,1711 | 0,0532 | 0,0121 | 0,9970 |
| \(m_i\) | 226,7 | 211,4 | 98,5 | 30,6 | 7,0 | 574,2 |
| \(f_i-m_i\) | 2,3 | -0,4 | -5,5 | 4,4 | 1,0 | — |
| \(\frac<(f_i-m_i)^2> | 0,02 | 0,00 | 0,31 | 0,63 | 0,16 | 1,12 |
Значение теста: \(X_e^2=1,12\)
Критическое значение статистики ищем в виде \(X_<кр>^2=X^2(\alpha,k-2)\), где α=0,05 и k=5, r=1
\(X_<кр>^2\approx 7,81\)
Получается, что: \(X_e^2\lt X_<кр>^2\)
Гипотеза \(H_0\) принимается.
Стрельба случайна.
И какой же ответ верный? Полученный в Примере 2 или в Примере 3?
Если посмотреть в расчетную таблицу для статистики \(X_e^2\) в Примере 2, основной вклад внесло слагаемое для \(x_i=7\). Оно равно 34,34 и поэтому сумма \(X_e^2=36,84\) в итоге велика. А в расчетной таблице Примера 3 такого выброса нет. Для объединенной варианты \(x_i=4,375\) слагаемое статистики равно 0,16 и сумма \(X_e^2=1,12\) в итоге мала.
Правильный ответ – в Примере 3.
Стрельба случайна.
Объясняем p-значения для начинающих Data Scientist’ов
Я помню, когда я проходил свою первую зарубежную стажировку в CERN в качестве практиканта, большинство людей все еще говорили об открытии бозона Хиггса после подтверждения того, что он соответствует порогу «пять сигм» (что означает наличие p-значения 0,0000003).
Тогда я ничего не знал о p-значении, проверке гипотез или даже статистической значимости.
Я решил загуглить слово — «p-значение», и то, что я нашел в Википедии, заставило меня еще больше запутаться…
При проверке статистических гипотез p-значение или значение вероятности для данной статистической модели — это вероятность того, что при истинности нулевой гипотезы статистическая сводка (например, абсолютное значение выборочной средней разницы между двумя сравниваемыми группами) будет больше или равна фактическим наблюдаемым результатам.
— Wikipedia
Хорошая работа, Википедия.
Ладно. Я не понял, что на самом деле означает р-значение.
Углубившись в область науки о данных, я наконец начал понимать смысл p-значения и то, где его можно использовать как часть инструментов принятия решений в определенных экспериментах.
Поэтому я решил объяснить р-значение в этой статье, а также то, как его можно использовать при проверке гипотез, чтобы дать вам лучшее и интуитивное понимание р-значений.
Также мы не можем пропустить фундаментальное понимание других концепций и определение p-значения, я обещаю, что сделаю это объяснение интуитивно понятным, не подвергая вас всеми техническими терминами, с которыми я столкнулся.
Всего в этой статье четыре раздела, чтобы дать вам полную картину от построения проверки гипотезы до понимания р-значения и использования его в процессе принятия решений. Я настоятельно рекомендую вам пройтись по всем из них, чтобы получить подробное понимание р-значений:
1. Проверка гипотез
Прежде чем мы поговорим о том, что означает р-значение, давайте начнем с разбора проверки гипотез, где р-значение используется для определения статистической значимости наших результатов.
Наша конечная цель — определить статистическую значимость наших результатов.
И статистическая значимость построена на этих 3 простых идеях:
Другими словами, мы создадим утверждение (нулевая гипотеза) и используем пример данных, чтобы проверить, является ли утверждение действительным. Если утверждение не соответствует действительности, мы выберем альтернативную гипотезу. Все очень просто.
Чтобы узнать, является ли утверждение обоснованным или нет, мы будем использовать p-значение для взвешивания силы доказательств, чтобы увидеть, является ли оно статистически значимым. Если доказательства подтверждают альтернативную гипотезу, то мы отвергнем нулевую гипотезу и примем альтернативную гипотезу. Это будет объяснено в следующем разделе.
Давайте воспользуемся примером, чтобы сделать эту концепцию более ясной, и этот пример будет использоваться на протяжении всей этой статьи для других концепций.
Пример. Предположим, что в пиццерии заявлено, что время их доставки составляет в среднем 30 минут или меньше, но вы думаете, что оно больше чем заявленное. Таким образом, вы проводите проверку гипотезы и случайным образом выбираете время доставки для проверки утверждения:
Одним из распространенных способов проверки гипотез является использование Z-критерия. Здесь мы не будем вдаваться в подробности, так как хотим лучше понять, что происходит на поверхности, прежде чем погрузиться глубже.
2. Нормальное распределение
Нормальное распределение — это функция плотности вероятности, используемая для просмотра распределения данных.
Нормальное распределение имеет два параметра — среднее (μ) и стандартное отклонение, также называемое сигма (σ).
Среднее — это центральная тенденция распределения. Оно определяет местоположение пика для нормальных распределений. Стандартное отклонение — это мера изменчивости. Оно определяет, насколько далеко от среднего значения склонны падать значения.
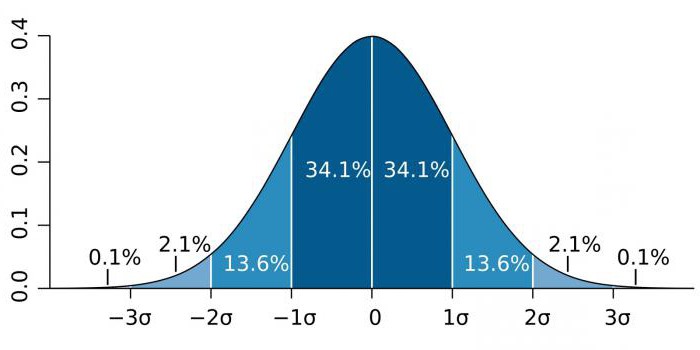
Нормальное распределение обычно связано с правилом 68-95-99.7 (изображение выше).
Классно. Теперь вы можете задаться вопросом: «Как нормальное распределение относится к нашей предыдущей проверке гипотез?»
Поскольку мы использовали Z-тест для проверки нашей гипотезы, нам нужно вычислить Z-баллы (которые будут использоваться в нашей тестовой статистике), которые представляют собой число стандартных отклонений от среднего значения точки данных. В нашем случае каждая точка данных — это время доставки пиццы, которое мы получили.
Обратите внимание, что когда мы рассчитали все Z-баллы для каждого времени доставки пиццы и построили стандартную кривую нормального распределения, как показано ниже, единица измерения на оси X изменится с минут на единицу стандартного отклонения, так как мы стандартизировали переменную, вычитая среднее и деля его на стандартное отклонение (см. формулу выше).
Изучение стандартной кривой нормального распределения полезно, потому что мы можем сравнить результаты теста с ”нормальной» популяцией со стандартизированной единицей в стандартном отклонении, особенно когда у нас есть переменная, которая поставляется с различными единицами.
Z-оценка может сказать нам, где лежат общие данные по сравнению со средней популяцией.
Мне нравится, как Уилл Кёрсен выразился: чем выше или ниже Z-показатель, тем менее вероятным будет случайный результат и тем более вероятным будет значимый результат.
Но насколько высокий (или низкий) показатель считается достаточно убедительным, чтобы количественно оценить, насколько значимы наши результаты?
Кульминация
Здесь нам нужен последний элемент для решения головоломки — p-значение, и проверить, являются ли наши результаты статистически значимыми на основе уровня значимости (также известного как альфа), который мы установили перед началом нашего эксперимента.
3. Что такое P-значение?
Наконец… Здесь мы говорим о р-значении!
Все предыдущие объяснения предназначены для того, чтобы подготовить почву и привести нас к этому P-значению. Нам нужен предыдущий контекст и шаги, чтобы понять это таинственное (на самом деле не столь таинственное) р-значение и то, как оно может привести к нашим решениям для проверки гипотезы.
Если вы зашли так далеко, продолжайте читать. Потому что этот раздел — самая захватывающая часть из всех!
Вместо того чтобы объяснять p-значения, используя определение, данное Википедией (извини Википедия), давайте объясним это в нашем контексте — время доставки пиццы!
Напомним, что мы произвольно отобрали некоторые сроки доставки пиццы, и цель состоит в том, чтобы проверить, превышает ли время доставки 30 минут. Если окончательные доказательства подтверждают утверждение пиццерии (среднее время доставки составляет 30 минут или меньше), то мы не будем отвергать нулевую гипотезу. В противном случае мы опровергаем нулевую гипотезу.
Поэтому задача p-значения — ответить на этот вопрос:
Если я живу в мире, где время доставки пиццы составляет 30 минут или меньше (нулевая гипотеза верна), насколько неожиданными являются мои доказательства в реальной жизни?
Р-значение отвечает на этот вопрос числом — вероятностью.
Чем ниже значение p, тем более неожиданными являются доказательства, тем более нелепой выглядит наша нулевая гипотеза.
И что мы делаем, когда чувствуем себя нелепо с нашей нулевой гипотезой? Мы отвергаем ее и выбираем нашу альтернативную гипотезу.
Если р-значение ниже заданного уровня значимости (люди называют его альфа, я называю это порогом нелепости — не спрашивайте, почему, мне просто легче понять), тогда мы отвергаем нулевую гипотезу.
Теперь мы понимаем, что означает p-значение. Давайте применим это в нашем случае.
P-значение в расчете времени доставки пиццы
Теперь, когда мы собрали несколько выборочных данных о времени доставки, мы выполнили расчет и обнаружили, что среднее время доставки больше на 10 минут с p-значением 0,03.
Это означает, что в мире, где время доставки пиццы составляет 30 минут или меньше (нулевая гипотеза верна), есть 3% шанс, что мы увидим, что среднее время доставки, по крайней мере, на 10 минут больше, из-за случайного шума.
Чем меньше p-значение, тем более значимым будет результат, потому что он с меньшей вероятностью будет вызван шумом.
В нашем случае большинство людей неправильно понимают р-значение:
Р-значение 0,03 означает, что есть 3% (вероятность в процентах), что результат обусловлен случайностью — что не соответствует действительности.
Р-значение ничего не *доказывает*. Это просто способ использовать неожиданность в качестве основы для принятия разумного решения.
— Кэсси Козырков
Вот как мы можем использовать p-значение 0,03, чтобы помочь нам принять разумное решение (ВАЖНО):
По моему мнению, p-значения используются в качестве инструмента для оспаривания нашего первоначального убеждения (нулевая гипотеза), когда результат является статистически значимым. В тот момент, когда мы чувствуем себя нелепо с нашим собственным убеждением (при условии, что р-значение показывает, что результат статистически значим), мы отбрасываем наше первоначальное убеждение (отвергаем нулевую гипотезу) и принимаем разумное решение.
4. Статистическая значимость
Наконец, это последний этап, когда мы собираем все вместе и проверяем, является ли результат статистически значимым.
Недостаточно иметь только р-значение, нам нужно установить порог (уровень значимости — альфа). Альфа всегда должна быть установлена перед экспериментом, чтобы избежать смещения. Если наблюдаемое р-значение ниже, чем альфа, то мы заключаем, что результат является статистически значимым.
Основное правило — установить альфа равным 0,05 или 0,01 (опять же, значение зависит от вашей задачи).
Как упоминалось ранее, предположим, что мы установили альфа равным 0,05, прежде чем мы начали эксперимент, полученный результат является статистически значимым, поскольку р-значение 0,03 ниже, чем альфа.
Для справки ниже приведены основные этапы всего эксперимента:
Если вы хотите узнать больше о статистической значимости, не стесняйтесь посмотреть эту статью — Объяснение статистической значимости, написанная Уиллом Керсеном.
Последующие размышления
Здесь много чего нужно переваривать, не так ли?
Я не могу отрицать, что p-значения по своей сути сбивают с толку многих людей, и мне потребовалось довольно много времени, чтобы по-настоящему понять и оценить значение p-значений и то, как они могут быть применены в рамках нашего процесса принятия решений в качестве специалистов по данным.
Но не слишком полагайтесь на p-значения, поскольку они помогают только в небольшой части всего процесса принятия решений.
Я надеюсь, что мое объяснение p-значений стало интуитивно понятным и полезным в вашем понимании того, что в действительности означают p-значения и как их можно использовать при проверке ваших гипотез.
Сам по себе расчет р-значений прост. Трудная часть возникает, когда мы хотим интерпретировать p-значения в проверке гипотез. Надеюсь, что теперь трудная часть станет для вас немного легче.
Если вы хотите узнать больше о статистике, я настоятельно рекомендую вам прочитать эту книгу (которую я сейчас читаю!) — Практическая статистика для специалистов по данным, специально написанная для data scientists, чтобы разобраться с фундаментальными концепциями статистики.
Узнайте подробности, как получить востребованную профессию с нуля или Level Up по навыкам и зарплате, пройдя платные онлайн-курсы SkillFactory: