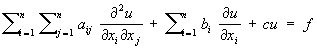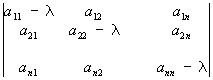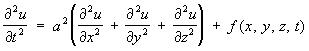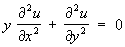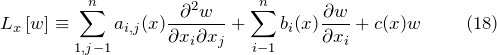что такое уравнение в физике

Уравнения математической физики

Полезное

Смотреть что такое «Уравнения математической физики» в других словарях:

УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ — дифференциальные уравнения с частными производными, интегральные уравнения, к которым приводит математический анализ физических явлений. См., напр., Волновое уравнение, Лапласа уравнение, Теплопроводности уравнение … Большой Энциклопедический словарь

уравнения математической физики — дифференциальные уравнения с частными производными, интегральные уравнения, к которым приводит математический анализ физических явлений. См., например, Волновое уравнение, уравнение Лапласа, уравнение теплопроводности. * * * УРАВНЕНИЯ… … Энциклопедический словарь

УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ — дифференциальные ур ния с частными производными, интегральные ур ния, к к рым приводит матем. анализ физ. явлений. См., напр., Волновое уравнение, Лапласа уравнение, Теплопроводности уравнение … Естествознание. Энциклопедический словарь

НЕЛИНЕЙНЫЕ УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ — ур ния, не обладающие свойством линейности; применяются в физике как матем. модели нелинейных явлений в разл. сплошных средах. Н. у. м. ф. важная часть матем. аппарата, используемого в фундам. физ. теориях: теории тяготения и квантовой теории… … Физическая энциклопедия

МАТЕМАТИЧЕСКОЙ ФИЗИКИ УРАВНЕНИЯ — уравнения, описывающие математические модели физических явлений. М. ф. у. часть предмета математической физики. Многие явления физики и механики (гидро и газодинамики, упругости, электродинамики, оптики, теории переноса, физики плазмы, квантовой… … Математическая энциклопедия

МАТЕМАТИЧЕСКОЙ ФИЗИКИ УРАВНЕНИЯ — ур ния, описывающие матем. модели физ. явлений. Теория этих моделей (математическая физи к а) занимает промежуточное положение между физикой и математикой. При построении моделей используют физ. законы, однако методы исследования полученных ур… … Физическая энциклопедия

МАТЕМАТИЧЕСКОЙ ФИЗИКИ УРАВНЕНИЯ — дифференц. ур ния с частными производными, интегральные и нек рые др. типы ур ний, к к рым приводит матем. анализ физ. явлений. М. ф. у. есть матем. выражение физ. законов, а входящие в них величины имеют непосредств. физ. смысл. Наиболее важны… … Большой энциклопедический политехнический словарь

Уравнения мелкой воды — Механика сплошных сред … Википедия

Уравнения Максвелла — Классическая электродинамика … Википедия

Источник

Уравнения математической физики в действии

Сегодня поговорим о примерах в дисциплине уравнения математической физики общими словами без погружения в сухой, академический язык и множества формул.

Ну это было уже давно, лекций не осталось, практика забылась, из головы все выветрилось как талая вода. Вот пример волны наглядный:

Волна

Как бы это уравнение бегущей волны с незакрепленными концами. Я мало что знаю об волнах, даже на уровне физики школьного курса, что-то типа амплитуды, периода, волнового числа и всего такого. Волны бывают продольные, поперечные, сферические, спиральные и другие. Это я только что прочитал на википедии.

Данный код ниже представляет практический интерес.

Как видите есть две функции, ksi и fi, они заданы тригонометрическими функциями sin, cos. Они характеризуют нашу волну. Там же есть аргументы функций 15*x и 18*x. Если, например увеличивать число 15 или число 18, то количество холмов будет увеличиваться, по-умному это значит, что чем большее число мы впишем в скобки, тем самым мы увеличиваем количество периодов функций данных, которые уместятся в заданный промежуток числа x. При увеличении будет сжиматься график вдоль оси Ox.

Икс то мы не увеличивали, шаг остался тем же около 0.01. Если мы будем уменьшать данные аргументы, то количество полных периодов функций будет меньше и как бы график растянется вдоль оси Ox.

А если мы вынесем за скобки и будем увеличивать/уменьшать само значение функции, как на коде выше, то будет растягиваться/сжиматься вдоль оси ординат, то есть вдоль оси Oy. Что показано на графиках ниже.

Здесь растяжение настолько большое что не вмещается в рабочее пространство и надо увеличивать рабочее пространство сцены и отдалять наблюдательное око.

А ниже наоборот сжатие относительно оси ординат.

Дело в том, я вот заметил, что каждое объяснение волн очень сложное, трудно выстроить в голове какие-либо упорядоченные знания об этом. Но я решил, что буду заниматься теперь только самыми насущными вещами, а не чтением гуманитарных статеек в интернете. Я очень много времени потратил на безделье и чтение всяких новостей, я превратился в гуманитария и не заметил.

С другой стороны, а как реализовать эти знания и монетизировать их? Не думаю, что есть вакансии, с требованием к программисту рисовать волны в браузере.

А вот второй пример посложнее, где уравнение окружность:

Волновая окружность

Хотелось сделать такой круг с волнами в виде, который похож на ютубе видел, как анимация голосовых волн от микрофона, но не получилось.

Здесь также можно увеличивать аргумент или/и значение функции и будет весьма интересно просмотреть результат.

Перейдем к следующему примеру, это концентрические окружности с волновым движением по оси Y:

Псевдо-мембрана

Чем-то похоже на изделие №1. Тот же принцип, но уже по массиву колец изменяется график, все кольцо увеличивается и уменьшается на одно значение, а другое кольцо уже на другое.

Чтобы улучшить вид, надо уменьшить шаг до тысячной доли, увеличить размер массива vertices в 10 раз, тогда не будет видно разрезов и будет идеально.

Глаз в положении 0,0,2

Резюмируя, хочу сказать вот многие говорили: «Зачем эти синусы и косинусы нужны?»

Вот для этого и многих других вещей, я, например написал об этом здесь, кто-то еще что-то придумает получше. Хотя трудно найти веб-программиста-математика-физика-художника, адская смесь получается.

Да, статья получилась не особо научной и в некотором роде объективной, но надо было чем-то заполнить пространство между картинками, спасибо у меня все!

Источник

Основные типы уравнений математической физики

Основные типы уравнений

К основным уравнениям математической физики относятся следующие дифференциальные уравнения в частных производных второго порядка.

1. Волновое уравнение:

.

Это уравнение является простейшим уравнением гиперболического типа. К его исследованию приводит изучение процессов поперечных колебаний струны, продольных колебаний стержня, электрических колебаний в проводах и т. д.

2. Уравнение теплопроводности, или уравнение Фурье:

.

Это уравнение является простейшим уравнением параболического типа. К его исследованию приводит рассмотрение процессов распространения тепла, фильтрации жидкости и газа в пористой среде, изучение некоторых вопросов теории вероятностей и т. д.

3. Уравнение Лапласа:

.

Это уравнение относится к простейшим уравнениям эллиптического типа. К его исследованию приводит изучение задач об электрических и магнитных полях, о стационарном тепловом состоянии, задач гидродинамики и т. д.

В выписанных уравнениях искомая функция u зависит от двух переменных t, x или x, y. Рассматриваются также уравнения и для функций с большим числом переменных. Например, волновое уравнение с тремя независимыми переменными имеет вид

,

и уравнение Лапласа

.

Уравнение колебаний струны.

Формулировка краевой задачи

В математической физике струной называют гибкую упругую нить. Пусть струна в начальный момент времени расположена на отрезке 0≤x≤l оси Ox. Предположим, что ее концы закреплены в точках x=0 и x=l. Если струну отклонить от первоначального положения, а потом предоставить самой себе или придать ее точкам некоторую скорость, то точки струны будут совершать движение. Задача заключается в определении формы струны в любой момент времени и в определении закона движения каждой точки струны в зависимости от времени.

Если предположить, что движение точек струны происходит перпендикулярно оси Ox и в одной плоскости, то процесс колебания струны описывается одной функцией u(x,t), которая определяет величину перемещения точки струны с абсциссой x в момент t.

Доказано, что при отсутствии внешней силы функция u(x,t) должна удовлетворять дифференциальному уравнению в частных производных второго порядка

.

Для полного определения движения струны одного уравнения недостаточно. Искомая функция u(x,t) должна удовлетворять граничным условиям, указывающим, что делается на концах струны (при x=0 и x=l), и начальным условиям, описывающим состояние струны в начальный момент (t=0). Совокупность граничных и начальных условий называется краевыми условиями.

Пусть, например, концы струны при x=0 и x=l неподвижны. Тогда при любом t должны выполняться равенства

Это – граничные условия для рассматриваемой задачи. В начальный момент t=0 струна имеет определенную форму, которую мы ей придали. Пусть эта форма определяется функцией f(x), т. е.

Далее в начальный момент должна быть задана скорость в каждой точке струны, которая определяется функцией φ(x), т. е.

.

Эти два условия называются начальными условиями.

Колебания бесконечной струны.

Формула Даламбера решения задачи Коши

для волнового уравнения

Прежде чем решать задачу о колебаниях закрепленной струны, рассмотрим более простую задачу – о колебаниях бесконечной струны. Если представить очень длинную струну, то ясно, что на колебания, возникающие в ее средней части, концы струны не будут оказывать заметного влияния.

Рассматривая свободные колебания, мы должны решить однородное уравнение

при начальных условиях

, ,

где функции f(x) и g(x) заданы на всей числовой оси. Такая задача называется задачей с начальными условиями или задачей Коши.

Преобразуем волновое уравнение к каноническому виду, содержащему смешанную производную. Уравнение характеристик

распадается на два уравнения:

интегралами которых служат прямые

Введем новые переменные ξ=x – at, η=x + at и запишем волновое уравнение для переменных ξ и η.

, ,

,

,

и подставляя их в исходное уравнение, видим, что уравнение колебания струны в новых координатах будет

.

Интегрируя полученное равенство по η при фиксированном ξ, придем к равенству . Интегрируя это равенство по ξ при фиксированном η, получим

,

где φ и ψ являются функциями только переменных ξ и η соответственно. Следовательно, общим решением исходного уравнения является функция

. (8)

Найдем функции φ и ψ так, чтобы удовлетворялись начальные условия:

.

,

.

Интегрируя последнее равенство, получим:

,

где х0 и С – постоянные. Из системы уравнений

Таким образом, мы определили функции φ и ψ через заданные функции f и g, причем полученные равенства должны иметь место для любого значения аргумента. Подставляя в (8) найденные значения φ и ψ, будем иметь

.

Найденное решение называется формулой Даламбера решения задачи Коши для волнового уравнения

Пример. Решить уравнение при начальных условиях , .

Используя формулу Даламбера, сразу получаем

.

Решение волнового уравнения

методом разделения переменных

Метод разделения переменных применяется для решения многих задач математической физики. Пусть требуется найти решение волнового уравнения

, (9)

удовлетворяющее краевым условиям

u(x,0)=f(x), . (12),(13)

Частное решение уравнения (9), удовлетворяющее граничным условиям (10) и (11), ищут в виде произведения двух функций:

Подставляя функцию u(x,t) в уравнение (9) и преобразовывая его, получим

.

В левой части этого уравнения стоит функция, которая не зависит от x, а в правой – функция, не зависящая от t. Равенство возможно только в том случае, когда левая и правая части не зависят ни от x, ни от t, т. е. равны постоянному числу. Обозначим

, где λ>0. (14)

Из этих уравнений получаем два однородных дифференциальных уравнения второго порядка с постоянными коэффициентами

и . (15)

Общее решение этих уравнений

,

,

где A, B, C, D – произвольные постоянные.

Постоянные A и B подбирают так, чтобы выполнялись условия (10) и (11), из которых следует, что X(0)=X(l)=0, так как T(t)≠0 (в противном случае u(x,t)=0). Учитывая полученные равенства, находим

А=0 и .

Так как B≠0 (иначе, было бы X=0 и u=0, что противоречит условию), то должно выполняться равенство

,

.

Найденные значения λ называют собственными значениями для данной краевой задачи. Соответствующие им функции X(x) называются собственными функциями.

Заметим, что, если в равенстве (14) вместо – λ взять число λ (λ>0), то первое из уравнений (15) будет иметь решение в виде

.

Отличное от нуля решение в такой форме не может удовлетворять граничным условиям (10) и (11).

Зная , можем записать

.

Для каждого n получаем решение уравнения (9)

.

Так как исходное уравнение (9) линейное и однородное, то сумма решений также является решением, и потому функция

(16)

будет решением дифференциального уравнения (9), удовлетворяющим граничным условиям (10) и (11).

Найденное частное решение должно еще удовлетворять начальным условиям (12) и (13). Из условия (12) получим

.

Далее, дифференцируя члены ряда (16) по переменной t, из условия (13) будем иметь

.

Правые части двух последних равенств есть ряды Фурье для функций f(x) и φ(x), разложенных по синусам на интервале (0, l). Поэтому

. (17)

Итак, ряд (16), для которого коэффициенты Cn и Dn определяются по выписанным формулам, если он допускает двукратное почленное дифференцирование, представляет решение уравнения (9), удовлетворяющее граничным и начальным условиям.

Пример. Найти решение краевой задачи для волнового уравнения

, 0

Источник

Уравнения математической физики

Дифференциальные уравнения математической физики

Математические модели естественнонаучных явлений и процессов зачастую представляют собой задачи, содержащие дифференциальные уравнения с частными производными первого и второго порядков. Дифференциальные уравнения существенные для физики, механики техники называют дифференциальными уравнениями математической физики.

Каждое уравнение математической физики описывает бесконечное множество качественно аналогичных явлений или процессов, так как дифференциальные уравнения, которыми занимается математическая физика, имеют бесконечное множество частных решений. Конкретное решение, описывающее рассматриваемое физическое явление, выделяется из множества частных решений с помощью начальных и граничных условий.

Общий вид дифференциального уравнения в частных производных первого порядка относительно неизвестной искомой функции таков:

Если F является линейной функцией относительно старших производных, то есть:

данное уравнение называется квазилинейным дифференциальным уравнением.

Если функции не зависят от u, а зависимость P от u линейна, то есть , тогда уравнение (2) называется линейным. Если , то уравнение (2) называется однородным линейным дифференциальным уравнением в частных производных первого порядка.

Решений уравнений математической физики

Рассмотрим квазилинейное дифференциальное уравнение в частных производных первого порядка:

Для получения общего решения уравнения (3) рассматривают характеристическую систему обыкновенных дифференциальных уравнений:

Если с=0, то система сводится к одному уравнению .

Если общий интеграл уравнения, тогда – общее решение.

Само дифференциальное уравнение содержит в себе только самую общую информацию об описываемом процессе. Необходимо задание начальных и граничных условий, для конкретизации.

Дифференциальные уравнения математической физики второго порядка

Большое количество процессов и явлений в физике описывается с помощью дифференциальных уравнений второго порядка в частных производных, это связано с тем, что фундаментальные законы физики – законы сохранения – записываются в терминах вторых производных. Методы решения уравнений математической физики зависят от типа к которому принадлежит рассматриваемое уравнение. Выделяют три основных типа дифференциальных уравнений с частными производными второго порядка, поиск решения которых имеют качественные различия: уравнения параболического, гиперболического и эллиптического типов.

Рассмотрим линейное уравнение с частными производными второго порядка с двумя независимыми переменными:

где a, b, c некоторые функции от x, y, имеющие непрерывные производные до второго порядка включительно.

Уравнение (5) принадлежит в точке (x, y)

где — независимые переменные. Кроме того — дважды дифференцируемая функция в рассматриваемой области. Уравнение (6) так же как и уравнение теплопроводности имеет только один член высшей производной.

первая каноническая форма:

где — независимые переменные,

вторая каноническая форма:

где . Левая часть уравнения (8) полностью совпадает с частью волнового уравнения.

где — независимые переменные. Левая часть этого уравнения совпадает с левой частью уравнения Лапласа.

Для того чтобы привести уравнение (5) к каноническому виду, надо записать так называемое характеристическое уравнение (10):

которое распадается на два уравнения:

и найти их общие интегралы.

В общем случае линейное уравнение с частными производными второго порядка параболического типа с n независимыми переменными можно записать так:

0\]» title=»Rendered by QuickLaTeX.com»/>

Уравнения параболического типа описывают неустановившиеся тепловые, диффузионные процессы, которые зависят от времени.

Уравнение (13) называют однородным, если =0.

Довольно часто при решении уравнения (13) ставят так называемую задачу Коши. В которой, требуется найти функцию w, удовлетворяющую уравнению (13) (при -эвклидово пространство) и начальном условии w=f(x) при t=0 и граничному условию:

0\right)\qquad (14)\]» title=»Rendered by QuickLaTeX.com»/>

В общем случае — линейный дифференциальный оператор первого порядка по пространственным переменным, коэффициенты которого зависят от x и t.

Начальное условие называют однородным, если f(x)=0. Граничное условие называют однородным, если .

В общем случае линейное уравнение с частными производными второго порядка гиперболического типа с n независимыми переменными можно записать так:

где линейный дифференциальный оператор определен формулам (14). Уравнениями гиперболического типа описываются неустановившиеся волновые процессы, зависящие от времени.

Граничные условия задаются (14).

Уравнения эллиптического типа

В общем случае линейное уравнение с частными производными второго порядка эллиптического типа с n независимыми переменными можно записать в виде:

0\]» title=»Rendered by QuickLaTeX.com»/>

Уравнения эллиптического типа описывают установившиеся тепловые, диффузионные и другие процессы, которые не зависят от времени. Уравнение (18) называется однородным, если

Граничные условия для эллиптического уравнения записывают так:

В общем случае — линейный дифференциальный оператор первого порядка.

Наиболее часто в прикладных примерах при описании различных процессов, происходящих в изотропных средах коэффициенты

таковыми и мы будем считать коэффициенты .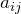

Для любых уравнений в частных производных второго порядка в зависимости от вида граничных условий принято выделять четыре типа краевых задач.

Первая краевая задача. На границе области S функция w(x,t) принимает заданные значения:

Вторая краевая задача. На границе области S задается производная по (внешней) нормали:

Третья краевая задача. На границе области S задана линейная связь между искомой функцией и ее производной по нормали:

Чаще всего В задачах массопереноса, где w – концентрация, граничное условие (22) при описывает поверхностную химическую реакцию.

Смешанные краевые задачи. В этом случае на различных участках границы S задают различные граничные условия.

Методы решения уравнений математической физики

Все методы решения уравнений математической физики можно разделить на две большие группы:

Среди аналитических методов решения уравнений следует выделить:

Среди численных методов решения уравнений математической физики следует выделить:

Примеры решения задач

Характеристическое уравнение для (1.1) имеет вид:

, где C- произвольная постоянная.

Общее решение уравнения (1.1), имеет вид бегущей волны:

из (1.3) видно, что а — скорость переноса. Так как 0″ title=»Rendered by QuickLaTeX.com» height=»12″ width=»44″ style=»vertical-align: 0px;»/>, то волна бежит слева направо. Подставим начальное условие, получим:

Получаем: .

ОтветФункция , является решением уравнения переноса при заданном начальном условии.

Задание

Решить задачу об остывании шара радиуса R, на поверхности которого поддерживается температура равная нулю. Начальная температура шара равна

0\qquad (2.1)\]» title=»Rendered by QuickLaTeX.com»/>

при начальном условии

и при граничном условии u(R,t)=0

Задачу можно решать методом Фурье (разделения переменных), представляя частное решение уравнения (2.1), удовлетворяющее граничному условию, в виде произведения:

Подставим (2.2) в (2.1), получим:

Таким образом, задача на собственные значения имеет вид:

Полагая w = rv, приходим к следующей задаче:

Задача имеет дискретный спектр собственных значений и собственных функций

Собственные значения и собственные функции краевой задачи, как известно, даются формулами:

Кроме того, из (2.3) имеем:

. Общее решение такого уравнения:

Так, можно построить набор частных решений вида (2.2) :

Суперпозиция образует ряд: (2.7)

Ряд (2.7) удовлетворяет уравнению (2.1) и граничному условию.

Выберем , используя начальное условие, подставим в (2.7) t=0:

В соответствии с теоремой Стеклова, в этом разложении функции 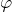(r) в ряд по собственным функциям задачи (2.4) коэффициенты могут быть найдены по формуле:

Следовательно, решение задачи вычисляется по формуле

Источник