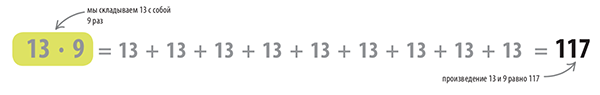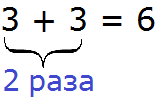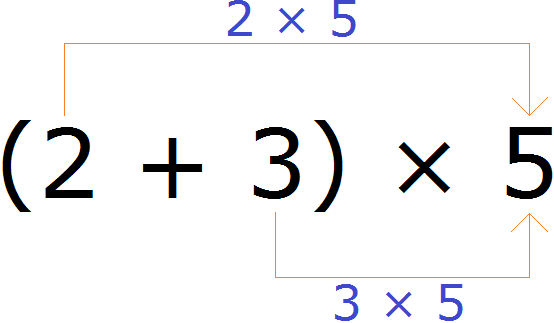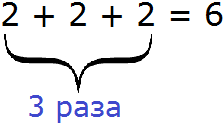что такое умножение и деление

Правила умножения и деления

После того, как выучена таблица умножения, школьникам объясняют правила умножения и деления, учат использовать их при вычислении математических выражений.

Что такое умножение? Это умное сложение

При сложении и вычитании, умножении и делении чисел в простых выражениях у детей не возникает трудностей:

В таких вычислениях необходимо только знать правила сложения и вычитания и таблицу умножения.
Когда начинаются более сложные упражнения, примеры состоят из двух и более действий, да еще и со скобками, при решении у детей появляются ошибки. И главная из них – неправильный порядок действий.

Да какая разница?

Действительно, настолько ли это важно – какое действие в примере выполнить первым, какое вторым?

Если мы будем выполнять действия по порядку, получим:

Получили два разных ответа. Но так быть не должно, следовательно, порядок выполнения действий имеет значение. Тем более, если в выражении имеются скобки:

Пробуем решить двумя способами:

Ответы разные, а для того чтобы определить порядок действий, в выражении стоят скобки – они показывают, какое действие нужно выполнить первым. Значит, правильным будет такое решение:

Другого решения у ответа у примера быть не должно.

Что важнее – умножение или сложение?

При решении примеров
Расставь порядок действий.
Умножить или разделить – на первом месте.

Для выражений, в которых присутствуют не сложение либо вычитание, а умножение или деление, действует то же правило: все действия с числами выполняются по порядку, начиная с левого:

Сложнее случай – когда в одной задаче встречаются умножение или деление со сложением или вычитанием. Каков порядок вычислений тогда?

Если выполнять все действия по порядку, сначала деление, затем сложение. В итоге получим:

Значит, пример решен правильно. А если в нем будут скобки?

То, что заключено в скобки, всегда в приоритете. Для того они и стоят в выражении. Поэтому порядок вычислений в подобных выражениях будет следующим:

81 : 9 + (6 – 2) + 3 = 16.

А что будет приоритетным: умножение — или деление, вычитание — или сложение, если оба действия встречаются в задаче? Ничего, они равны, в таком случае действует первое правило – действия производятся одно за другим, начиная слева.

Алгоритм решения выражения:

Ответ: 28 : (11 – 4) + 18 – (25 – 8) = 5.

Важно! Если в выражении есть буквенные обозначения, порядок действий остается прежним.

Математические действия с нулем

Круглый нуль такой хорошенький,
Но не значит ничегошеньки.

В примерах нуль как число не встречается, но он может быть результатом какого-либо промежуточного действия, например:

При умножении на 0 правило гласит, что в результате всегда получится 0. Почему? Объяснить можно просто: что такое умножение? Это одно и то же число, сложенное с себе подобным несколько раз. Иначе:

0 × 5 = 0 + 0 + 0 + 0 + 0 = 0;

Деление на 0 бессмысленно, а деление нуля на любое число даст в результате всегда 0:

0 : 5 = 0.

Да и как может быть иначе, когда делить-то нечего? Если у вас нет яблок, поделиться с друзьями вам нечем.

Напомним другие арифметические действия с нулем:

Умножение и деление на единицу

Математические действия с единицей отличаются от действий с нулем. При умножении или делении числа на 1 получается само первоначальное число:

7 × 1 = 7;

7 : 1 = 7.

Конечно, если у вас есть 7 друзей, и каждый подарил вам по конфете, у вас будет 7 конфет, а если вы их съели в одиночестве, то есть поделились лишь с самим собой, то все они и оказались в вашем желудке.

Вычисления с дробями, степенями и сложными функциями

Это сложные случаи вычислений, которые не рассматриваются в рамках начальной школы.

Умножение простых дробей друг на друга не представляется сложными, достаточно лишь перемножить числитель на числитель, а знаменатель – на знаменатель.
Пример:

После сокращения получаем:\(<<6>over\<40>>\) = \(<<3>over\<20>>\).

Деление простых дробей не так сложно, как кажется на первый взгляд. Достаточно лишь преобразовать задачу – превратить ее в пример с умножением. Сделать это просто – нужно перевернуть дробь так, чтобы знаменатель стал числителем, а числитель – знаменателем.
Пример:

Если в задаче встречается число, представленное в виде степени, его значение вычисляется прежде всех остальных (можете представить, что оно заключено в скобки – а действия в скобках выполняются первыми).
Пример:

Преобразовав число, представленное в виде степени, в обычное выражение с действием умножения, решить пример оказалось просто: сначала умножение, затем вычитание (потому что в скобках) и деление.

Поскольку такие функции изучаются только в рамках старшей школы, рассматривать их мы не будем, достаточно только сказать, что они, как и в случае со степенями, имеют приоритет при вычислении: сначала находится значение данного выражения, затем порядок вычислений обычный – скобки, умножение с делением, далее по порядку слева направо.

Главные правила по теме

Говоря о главных и неглавных математических действиях, нужно сказать, что четыре основных действия можно свести к двум: сложение и умножение. Если вычитание и деление представляется для школьников сложным, правила сложения и умножения они запоминают быстрее. Действительно, выражение 5 – 2 можно записать иначе:

В случаях с умножением действуют правила, схожие со свойствами сложения: от перестановки множителей произведение не изменится:

При решении сложных задач первое действие — то, которое выделено скобками, затем — деление или умножение, потом все остальные действия по порядку.
Когда нужно решить примеры без скобок, вначале выполняется умножение или деление, далее — вычитание либо сложение.

Источник

Что такое умножение и деление

Далеко не все дети понимают деление и умножение с первого раза, поэтому родителям приходится дома подробнее разбирать эти процессы. Сегодня расскажем, как это сделать проще для ребенка. В книге «Как объяснить ребенку математику» объяснения строятся на визуальных принципах. Так школьнику будет понятнее, а родителю легче построить общение.

Умножение чисел

При умножении второе число показывает, сколько раз нужно сложить первое число с самим собой. На рисунке ниже в каждой шеренге стоят 13 человек, а всего шеренг 9. Чтобы подсчитать общее количество людей, нужно число 13 сложить само с собой 9 раз. Это и будет произведением чисел 13 на 9.

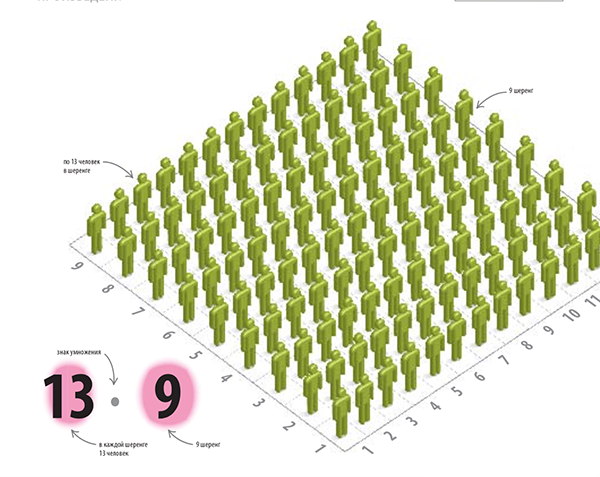
Иллюстрация из книги «Как объяснить ребенку математику»

Количество людей в шеренге (13) умножается на количество шеренг (9). Общее количество людей равно 117.

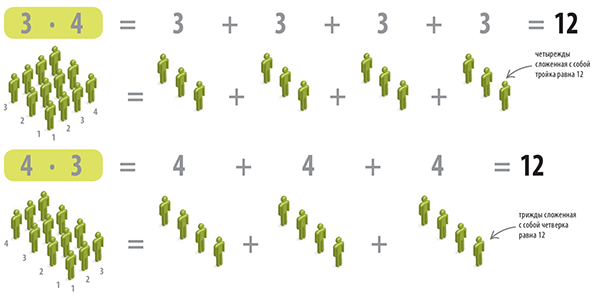
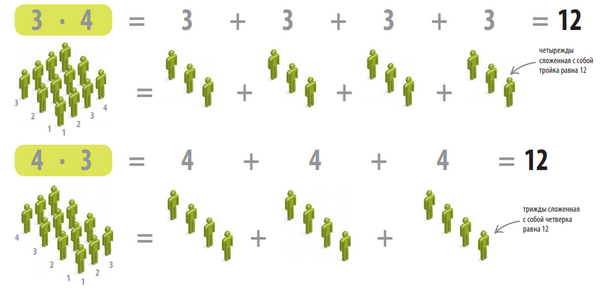
Не имеет значения, в каком порядке перемножаются числа: ответ будет одинаковым. Ниже показаны два способа, как можно вычислить произведение.

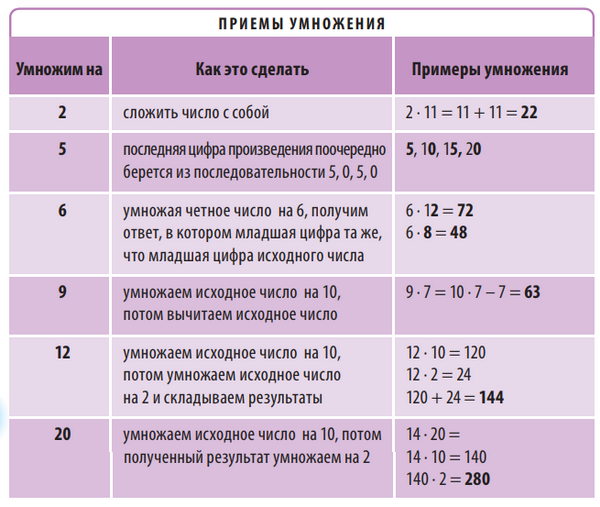
Некоторые числа легко умножать, зная особые приемы. Вот они.

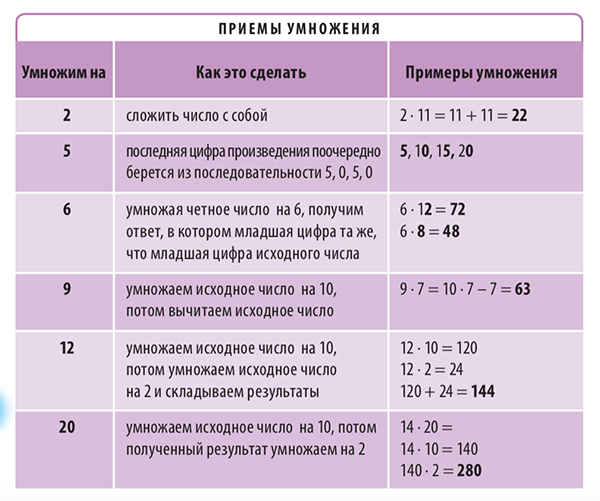
Таблица из книги «Как объяснить ребенку математику»

В таблице показаны приемы быстрого умножения на 2, 5, 6, 9, 12 и 20.

Деление чисел

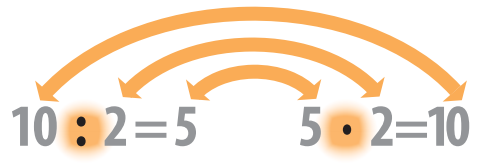
Деление позволяет найти, сколько раз одно число содержится в другом. Процесс деления можно представить, например, так: если 10 монет раздать 2 людям, то каждый получит по 5 монет. Или так: 10 монет, разложенные в стопки по 2 монеты, дадут 5 стопок.

Деление одного числа (делимого) на другое (делитель) показывает, сколько делителей содержится в делимом. Например, при делении 10 на 2 мы находим, сколько чисел 2 содержится в числе 10. Результат деления называется частным.

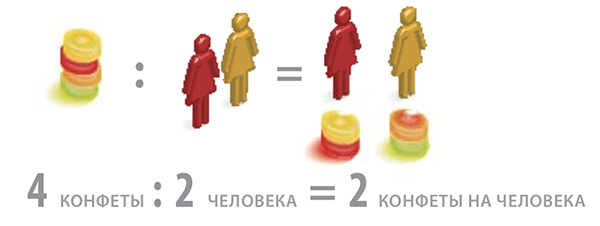
Деление как распределение. Из книги «Как объяснить ребенку математику»

Распределение чего-либо — это, по сути, операция деления. Так, если поровну распределить четыре конфеты между двумя людьми, у каждого из них будет по две конфеты.

Деление и умножение лучше рассматривать параллельно, чтобы ребенок увидел взаимосвязь. В книге «Как объяснить ребенку математику» есть объяснения более сложных операций, например, деления с остатком, умножения в столбик и так далее. Если визуально показать, как это делается, ребенку легче будет усвоить материал.

Рабочие тетради на деление и умножение

Если ваш ребенок освоил азы деления и умножения, то сейчас ему нужна практика. Японская система Kumon предлагает рабочие тетради «Математика. Деление. Уровень 4»

и «Математика. Умножение. Уровень 4». Постепенно, решая все более сложные задачи, ребенок научится работать с большими цифрами. Ниже — пример одного из последних заданий тетради с делениями.

Пример из тетради «Математика. Деление. Уровень 4»

Такие примеры ребенок научится решать легко и быстро, если тренироваться регулярно и по принципу от простого к сложному. Задания нужно усложнять постепенно, тогда школьник будет учиться с чувством «я могу!».

Источник

Порядок действий в математике

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные операции в математике

Порядок вычисления простых выражений

Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок:

Из этого правила становится яснее, какое действие выполняется первым. Универсального ответа нет, нужно анализировать каждый пример и подбирать ход решения самостоятельно.

Что первое, умножение или деление? — По порядку слева направо.

Сначала умножение или сложение? — Умножаем, потом складываем.

Порядок выполнения действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято вести записи слева направо. А необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Рассмотрим порядок арифметических действий в примерах.

Пример 1. Выполнить вычисление: 11- 2 + 5.

В нашем выражении нет скобок, умножение и деление отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычтем два из одиннадцати, затем прибавим к остатку пять и в итоге получим четырнадцать.

Вот запись всего решения: 11- 2 + 5 = 9 + 5 = 14.

Пример 2. В каком порядке выполнить вычисления в выражении: 10 : 2 * 7 : 5?

Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Сначала выполняем деление десяти на два, результат умножаем на семь и получившееся в число делим на пять.

Запись всего решения выглядит так: 10 : 2 * 7 : 5 = 5 * 7 : 5 = 35 : 5 = 7.

Пока новые знания не стали привычными, чтобы не перепутать последовательность действий при вычислении значения выражения, удобно над знаками арифметический действий расставить цифры, которые соответствуют порядку их выполнения.

Например, в такой последовательности можно решить пример по действиям:

Действия первой и второй ступени

В некоторых учебниках по математике можно встретить разделение арифметических действий на действия первой и второй ступени.

С этими терминами правило определения порядка выполнения действий звучит так:

Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем — действия первой ступени (сложение и вычитание).

Порядок вычислений в выражениях со скобками

Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:

Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.

Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.

Рассмотрим порядок выполнения действий на примерах со скобками.

Как правильно решить пример:

Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.

Подставляем полученные значения в исходное выражение:

Порядок действий: умножение, деление, и только потом — сложение. Получится:

10 + 2 * 8 : 2 = 10 + 16 : 2 = 10 + 8 = 18.

На этом все действия выполнены.

Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.

Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).

Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:

Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:

5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.

Исходное значение, после подстановки примет вид 9 + 26, и остается лишь выполнить сложение: 9 + 26 = 35.

Ответ: 9 + (5 + 1 + 4 * (2 + 3)) = 35.

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции — их значения нужно вычислить до выполнения остальных действий. При этом важно учитывать правила из предыдущих пунктов, которые задают очередность действий в математике.

Другими словами, перечисленные функции по степени важности можно приравнивать к выражению в скобках.

И, как всегда, рассмотрим, как это работает на примере.

В этом выражении есть степень 62. И нам нужно найти ее значение до выполнения остальных действий. Выполним возведение в степень: 62 = 36.

Подставляем полученное значение в исходное выражение:

Дальше нам уже все знакомо: выполняем действия в скобках, далее по порядку слева направо выполняем сначала умножение, деление, а затем — сложение и вычитание. Ход решения выглядит так:

Закрепить на практике тему «Порядок действий» можно на курсах по математике в Skysmart!

Источник

Что такое умножение и деление

Можно заставить ребенка просто решать скучные примеры (и ему будет совсем неинтересно), а можно предложить ему решить забавные текстовые задачки в тетради Kumon или сразиться в межпланетном рыцарском турнире на звание лучшего знатока дробей. Второй подход определенно занимательнее: ребенку гораздо больше понравится учить математику в игре.

Ребятам постарше также по душе будут игровые моменты в обучении. Ведь гораздо веселее изучать математику через яркое домино, чем читать длинные главы в учебнике.

Подготовили для вас несколько советов и подборку книг, которые помогут разложить умножение и деление по полочкам.

Умножаем

Что такое умножение? При умножении второе число показывает, сколько раз нужно сложить первое число с самим собой. На рисунке в каждой шеренге стоят 13 человек, а всего шеренг 9. Чтобы подсчитать общее количество людей, нужно число 13 сложить само с собой 9 раз. Это и будет произведением чисел 13 на 9.

Не имеет значения, в каком порядке перемножаются числа: ответ будет одинаковым. Ниже показаны два способа, как можно вычислить произведение.

Умножение на 10, 100, 1000 Для того чтобы умножить целое число на 10, 100, 1000 и т. д., нужно просто дописать справа от этого числа один нуль (0), два нуля (00), три нуля (000) и т. д.

Приемы умножения. Некоторые числа легко умножать, зная особые приемы. В таблице показаны приемы быстрого умножения на 2, 5, 6, 9, 12 и 20.

Делим

Деление позволяет найти, сколько раз одно число содержится в другом. Процесс деления можно представить, например, так: если 10 монет раздать 2 людям, то каждый получит по 5 монет. Или так: 10 монет, разложенные в стопки по 2 монеты, дадут 5 стопок.

Как выполняется деление? Деление одного числа (делимого) на другое (делитель) показывает, сколько делителей содержится в делимом. Например, при делении 10 на 2 мы находим, сколько чисел 2 содержится в числе 10. Результат деления называется частным.

Деление как распределение. Распределение чего-либо — это, по сути, операция деления. Так, если поровну распределить четыре конфеты между двумя людьми, у каждого из них будет по две конфеты.

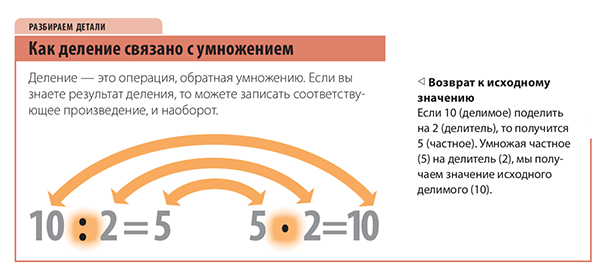
Как деление связано с умножением? Деление — это операция, обратная умножению. Если вы знаете результат деления, то можете записать соответствующее произведение, и наоборот.

Если 10 (делимое) поделить на 2 (делитель), то получится 5 (частное). Умножая частное (5) на делитель (2), мы получаем значение исходного делимого (10).

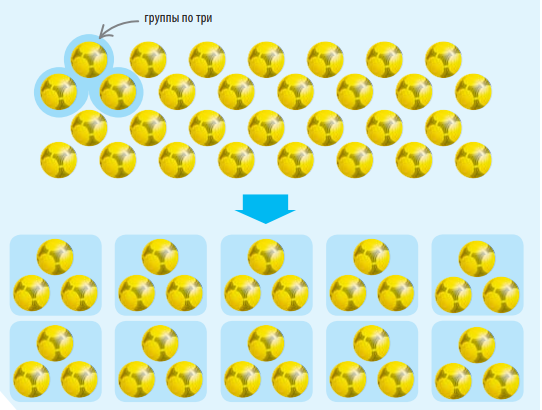
Другой подход к делению. Деление также показывает, сколько раз в делимом встречаются группы, равные делителю. Ответом будет то же самое частное. Получилось ровно 10 групп по 3 мяча (без остатка), поэтому 30 : 3 = 10. В этом примере 30 футбольных мячей делятся на группы по 3 мяча.

Книги и тетради, которые помогут закрепить навыки

Арифметикум

Домино, с которым ребенок научится хорошо складывать, вычитать, умножать и делить числа до 100. Игрок должен разместить карточку так, чтобы на оказавшихся рядом клеточках был написан пример и правильный ответ или два примера, в результате решения которых получится одно число.

Вокруг любой клеточки можно расположить сразу несколько карточек: по одной у каждой свободной стороны. Проверить вычисления игроки могут по цветным узорам: если узоры совпадают, ход сделан правильно.

Умножариум

Веселая игра поможет освоить математику

Это домино создано специально для легкого и увлекательного изучения таблицы умножения детьми: вместо традиционных точек на каждой карточке нанесены математические примеры и цифры. Совмещая клетку с примером (например, 5×8) и результат умножения (40), ребенок сразу видит, правильно ли он посчитал пример, благодаря цветовому паттерну, который должен совпасть на двух клетках.

Kumon спешит на помощь

У нас есть множество тетрадей разных уровней сложности, которые помогут выучить таблицу умножения на зубок.

KUMON. Математика. Умножение. Уровень 4

Эта яркая тетрадка научит ребенка умножать многозначные числа в столбик. Шаг за шагом он будет осваивать этот навык, его ждут примеры, которые будут постепенно усложняться, полезные подсказки и, конечно, ключи с ответами в конце тетради для самоконтроля.

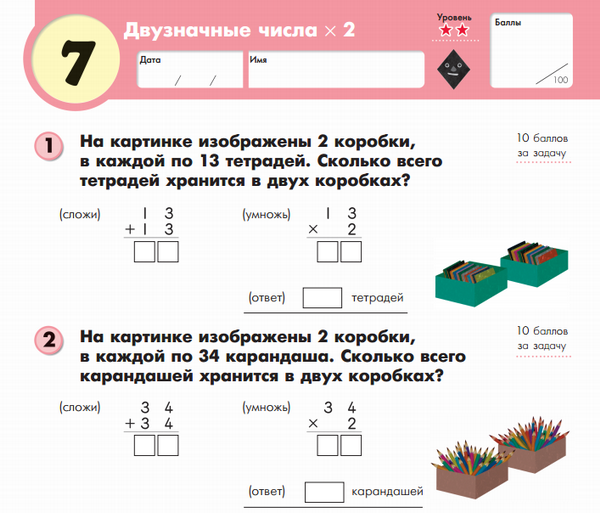
Простые задачки научат умножать. Пример из тетради

Kumon. Математика. Деление. Уровень 4

Выполняя задания в этой тетради, ваш ребёнок научится делить многозначные числа в столбик с остатком и без него. Продвигаясь вперёд небольшими последовательными шажками, он обретёт не только математические знания, но и уверенность в своих силах.

Межпланетный рыцарский турнир

Решая примеры из этой книги, ребенок примет участие в настоящем межпланетном состязании! Каждый правильный ответ — ты успешно атаковал противника, каждая ошибка — противник успешно атаковал тебя. Для убедительности в книге есть изображения персонажей, за которых нужно сыграть юному математику, и их соперников, а также фантастические истории про инопланетян. Всех героев можно раскрасить!

Источник

Умножение и деление целых чисел

При умножении и делении целых чисел применяется несколько правил. В данном уроке мы рассмотрим каждое из них.

При умножении и делении целых чисел следует обращать внимание на знаки чисел. От них будет зависеть какое правило применять. Необходимо также изучить несколько законов умножения и деления. Изучение этих правил позволит избежать некоторых досадных ошибок в будущем.

Законы умножения

Некоторые из законов математики мы рассматривали в уроке законы математики. Но мы рассмотрели не все законы. В математике немало законов и разумнее будет изучать их последовательно по мере необходимости.

Множимое показывает, что именно мы увеличиваем. В нашем примере мы увеличиваем число 3.

Множитель показывает во сколько раз нужно увеличить множимое. В нашем примере множитель это число 2. Этот множитель показывает во сколько раз нужно увеличить множимое 3. То есть в ходе операции умножения число 3 будет увеличено в два раза.

Произведение это собственно результат операции умножения. В нашем примере произведение это число 6. Это произведение является результатом умножения 3 на 2.

Выражение 3 × 2 также можно понимать, как сумму двух троек. Множитель 2 в таком случае будет показывать сколько раз нужно повторить число 3:

Таким образом, если число 3 повторить два раза подряд, получится число 6.

Переместительный закон умножения

Множимое и множитель называют одним общим словом – сомножители. Переместительный закон умножения выглядит следующим образом:

От перестановки мест сомножителей произведение не меняется.

Проверим так ли это. Умножим к примеру 3 на 5. Здесь 3 и 5 это сомножители.

Теперь поменяем местами сомножители:

В обоих случаях мы получаем ответ 15, поэтому между выражениями 3 × 5 и 5 × 3 можно поставить знак равенства, поскольку они равны одному тому же значению:

А с помощью переменных переместительный закон умножения можно записать так:

где a и b — сомножители

Сочетательный закон умножения

Этот закон говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.

К примеру, выражение 3 × 2 × 4 состоит из нескольких сомножителей. Чтобы его вычислить, можно перемножить 3 и 2, затем полученное произведение умножить на оставшееся число 4. Выглядеть это будет так:

3 × 2 × 4 = (3 × 2) × 4 = 6 × 4 = 24

Это был первый вариант решения. Второй вариант состоит в том, чтобы перемножить 2 и 4, затем полученное произведение умножить на оставшееся число 3. Выглядеть это будет так:

3 × 2 × 4 = 3 × (2 × 4) = 3 × 8 = 24

В обоих случаях мы получаем ответ 24. Поэтому между выражениями (3 × 2) × 4 и 3 × (2 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:

а с помощью переменных сочетательный закон умножения можно записать так:

a × b × c = (a × b) × c = a × (b × c)

где вместо a, b, c могут стоять любые числа.

Распределительный закон умножения

Распределительный закон умножения позволяет умножить сумму на число. Для этого каждое слагаемое этой суммы умножается на это число, затем полученные результаты складывают.

Например, найдём значение выражения (2 + 3) × 5

Выражение находящееся в скобках является суммой. Эту сумму нужно умножить на число 5. Для этого каждое слагаемое этой суммы, то есть числа 2 и 3 нужно умножить на число 5, затем полученные результаты сложить:

(2 + 3) × 5 = 2 × 5 + 3 × 5 = 10 + 15 = 25

С помощью переменных распределительный закон умножения записывается так:

(a + b) × c = a × c + b × c

где вместо a, b, c могут стоять любые числа.

Закон умножения на ноль

Этот закон говорит о том, что если в любом умножении имеется хотя бы один ноль, то в ответе получится ноль.

Произведение равно нулю, если хотя бы один из сомножителей равен нулю.

Например, выражение 0 × 2 равно нулю

Иными словами, если «ничего» увеличить в два раза или даже в миллион раз, всё равно получится «ничего».

И если в выражении 0 × 2 поменять местами сомножители, опять же получится ноль. Это мы знаем из предыдущего переместительного закона:

Примеры применения закона умножения на ноль:

В последних двух примерах имеется несколько сомножителей. Увидев в них ноль, мы сразу в ответе поставили ноль, применив закон умножения на ноль.

Мы рассмотрели основные законы умножения. Теперь рассмотрим самó умножение целых чисел.

Умножение целых чисел

Пример 1. Найти значение выражения −5 × 2

Это умножение чисел с разными знаками. −5 является отрицательным числом, а 2 – положительным. Для таких случаев нужно применять следующее правило:

Чтобы перемножить числа с разными знаками, нужно перемножить их модули, и перед полученным ответом поставить минус.

−5 × 2 = − (|−5| × |2|) = − (5 × 2) = − (10) = −10

Обычно записывают короче: −5 × 2 = −10

Любое умножение может быть представлено в виде суммы чисел. Например, рассмотрим выражение 2 × 3. Оно равно 6.

Множителем в данном выражение является число 3. Этот множитель показывает во сколько раз нужно увеличить двойку. Но выражение 2 × 3 также можно понимать как сумму трёх двоек:

То же самое происходит и с выражением −5 × 2. Это выражение может быть представлено в виде суммы

А выражение (−5) + (−5) равно −10. Мы это знаем из прошлого урока. Это сложение отрицательных чисел. Напомним, что результат сложения отрицательных чисел есть отрицательное число.

Пример 2. Найти значение выражения 12 × (−5)

Это умножение чисел с разными знаками. 12 – положительное число, (−5) – отрицательное. Опять же применяем предыдущее правило. Перемножаем модули чисел и перед полученным ответом ставим минус:

12 × (−5) = − (|12| × |−5|) = − (12 × 5) = − (60) = −60

Обычно решение записывают покороче:

Пример 3. Найти значение выражения 10 × (−4) × 2

Это выражение состоит из нескольких сомножителей. Сначала перемножим 10 и (−4), затем полученное число умножим на 2. Попутно применим ранее изученные правила:

Первое действие:

10 × (−4) = −(|10| × |−4|) = −(10 × 4) = (−40) = −40

Второе действие:

−40 × 2 = −(|−40 | × | 2|) = −(40 × 2) = −(80) = −80

Значит значение выражения 10 × (−4) × 2 равно −80

Запишем решение покороче:

10 × (−4) × 2 = −40 × 2 = −80

Пример 4. Найти значение выражения (−4) × (−2)

Это умножение отрицательных чисел. В таких случаях нужно применять следующее правило:

Чтобы перемножить отрицательные числа, нужно перемножить их модули и перед полученным ответом поставить плюс

(−4) × (−2) = |−4| × |−2| = 4 × 2 = 8

Плюс по традиции не записываем, поэтому просто записываем ответ 8.

Запишем решение покороче (−4) × (−2) = 8

Возникает вопрос почему при умножении отрицательных чисел вдруг получается положительное число. Давайте попробуем доказать, что (−4) × (−2) равно 8 и ни чему другому.

Сначала запишем следующее выражение:

Заключим его в скобки:

Прибавим к этому выражению наше выражение (−4) × (−2). Его тоже заключим в скобки:

Всё это приравняем к нулю:

Теперь начинается самое интересное. Суть в том, что мы должны вычислить левую часть этого выражения, и в результате получить 0.

Итак, первое произведение ( 4 × (−2) ) равно −8. Запишем в нашем выражении число −8 вместо произведения ( 4 × (−2) )

Теперь вместо второго произведения временно поставим многоточие

Теперь внимательно посмотрим на выражение −8 + … = 0. Какое число должно стоять вместо многоточия, чтобы соблюдалось равенство? Ответ напрашивается сам. Вместо многоточия должно стоять положительное число 8 и никакое другое. Только так будет соблюдаться равенство. Ведь −8 + 8 равно 0.

Возвращаемся к выражению −8 + ((−4) × (−2)) = 0 и вместо произведения ((−4) × (−2)) записываем число 8

Пример 5. Найти значение выражения −2 × (6 + 4)

Применим распределительный закон умножения, то есть умножим число −2 на каждое слагаемое суммы (6 + 4)

−2 × (6 + 4) = −2 × 6 + ( −2) × 4

Теперь выполним умножение, и сложим полученные результаты. Попутно применим ранее изученные правила. Запись с модулями можно пропустить, чтобы не загромождать выражение

Первое действие:

Второе действие:

Третье действие:

Значит значение выражения −2 × (6 + 4) равно −20

Запишем решение покороче:

−2 × (6 + 4) = (−12) + (−8) = −20

Пример 6. Найти значение выражения (−2) × (−3) × (−4)

Выражение состоит из нескольких сомножителей. Сначала перемножим числа −2 и −3, и полученное произведение умножим на оставшееся число −4. Запись с модулями пропустим, чтобы не загромождать выражение

Первое действие:

Второе действие:

Значит значение выражения (−2) × (−3) × (−4) равно −24

Запишем решение покороче:

Законы деления

Прежде чем делить целые числа, необходимо изучить два закона деления.

В первую очередь, вспомним из чего состоит деление. Деление состоит из трёх параметров: делимого, делителя и частного. Например, в выражении 8 : 2 = 4, 8 – это делимое, 2 – делитель, 4 – частное.

Делимое показывает, что именно мы делим. В нашем примере мы делим число 8.

Делитель показывает на сколько частей нужно разделить делимое. В нашем примере делитель это число 2. Этот делитель показывает на сколько частей нужно разделить делимое 8. То есть в ходе операции деления, число 8 будет разделено на две части.

Частное – это собственно результат операции деления. В нашем примере частное это число 4. Это частное является результатом деления 8 на 2.

Далее рассмотрим законы деления.

На ноль делить нельзя

Любое число запрещено делить на ноль.

Дело в том, что деление это действие, обратное умножению. Данную фразу можно понимать в прямом смысле. Например, если 2 × 5 = 10, то 10 : 5 = 2.

Видно, что второе выражение записано в обратном порядке. Если к примеру, у нас имеется два яблока и мы захотим увеличить их в пять раз, то мы запишем 2 × 5 = 10. Получится десять яблок. Затем, если мы захотим обратно уменьшить эти десять яблок до двух, то мы запишем 10 : 5 = 2

Точно так же можно поступать и с другими выражениями. Если к примеру, 2 × 6 = 12, то мы можем обратно вернуться к изначальному числу 2. Для этого достаточно записать выражение 2 × 6 = 12 в обратном порядке, разделяя 12 на 6

Теперь рассмотрим выражение 5 × 0. Мы знаем из законов умножения, что произведение равно нулю, если хотя бы один из сомножителей равен нулю. Значит и выражение 5 × 0 равно нулю

Если записать это выражение в обратном порядке, то получим:

Сразу в глаза бросается ответ 5, который получается в результате деления ноль на ноль. Это невозможно.

В обратном порядке можно записать и другое похожее выражение, например 2 × 0 = 0

В первом случае, разделив ноль на ноль мы получили 5, а во втором случае 2. То есть каждый раз деля ноль на ноль, мы можем получить разные значения, а это недопустимо.

Второе объяснение заключается в том, что разделить делимое на делитель означает найти такое число, которое при умножении на делитель даст делимое.

Например выражение 8 : 2 означает найти такое число, которое при умножении на 2 даст 8

Здесь вместо многоточия должно стоять число, которое при умножении на 2 даст ответ 8. Чтобы найти это число, достаточно записать это выражение в обратном порядке:

Получили число 4. Запишем его вместо многоточия:

Теперь представим, что нужно найти значение выражения 5 : 0. В данном случае 5 – это делимое, 0 – делитель. Разделить 5 на 0 означает найти такое число, которое при умножении на 0 даст 5

Здесь вместо многоточия должно стоять число, которое при умножении на 0 даст ответ 5. Но не существует числа, которое при умножении на ноль даёт 5.

Выражение … × 0 = 5 противоречит закону умножения на ноль, который утверждает, что произведение равно нулю, когда хотя бы один из сомножителей равен нулю.

А значит записывать выражение … × 0 = 5 в обратном порядке, деля 5 на 0 нет никакого смысла. Поэтому и говорят, что на ноль делить нельзя.

С помощью переменных данный закон записывается следующим образом:

, при b ≠ 0

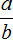
Это выражение можно прочитать так:

Число a можно разделить на число b, при условии, что b не равно нулю.

Свойство частного

Этот закон говорит о том, что если делимое и делитель умножить или разделить на одно и то же число, то частное не изменится.

Например, рассмотрим выражение 12 : 4. Значение этого выражения равно 3

Попробуем умножить делимое и делитель на одно и то же число, например на число 4. Если верить свойству частного, мы опять должны получить в ответе число 3

(12 × 4 ) : (4 × 4 )

(12 × 4 ) : (4 × 4 ) = 48 : 16 = 3

Теперь попробуем не умножить, а разделить делимое и делитель на число 4

(12 : 4 ) : (4 : 4 )

(12 : 4 ) : (4 : 4 ) = 3 : 1 = 3

Видим, что если делимое и делитель умножить или разделить на одно и то же число, то частное не меняется.

Мы рассмотрели два закона деления. Далее рассмотрим деление целых чисел.

Деление целых чисел

Пример 1. Найти значение выражения 12 : (−2)

Это деление чисел с разными знаками. 12 — положительное число, (−2) – отрицательное. Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить минус.

12 : (−2) = −(|12| : |−2|) = −(12 : 2) = −(6) = −6

Обычно записывают покороче:

Пример 2. Найти значение выражения −24 : 6

Это деление чисел с разными знаками. −24 – это отрицательное число, 6 – положительное. Опять же модуль делимого делим на модуль делителя, и перед полученным ответом ставим минус.

−24 : 6 = −(|−24| : |6|) = −(24 : 6) = −(4) = −4

Запишем решение покороче:

Пример 3. Найти значение выражения −45 : (−5)

Это деление отрицательных чисел. Чтобы решить этот пример, нужно модуль делимого разделить на модуль делителя, и перед полученным ответом поставить знак плюс.

−45 : (−5) = |−45| : |−5| = 45 : 5 = 9

Запишем решение покороче:

Пример 4. Найти значение выражения −36 : (−4) : (−3)

Согласно порядку действий, если в выражении присутствует только умножение или деление, то все действия нужно выполнять слева направо в порядке их следования.

Разделим −36 на (−4), и полученное число разделим на −3

Первое действие:

−36 : (−4) = |−36| : |−4| = 36 : 4 = 9

Второе действие:

9 : (−3) = −(|9| : |−3|) = −(9 : 3) = −(3) = −3

Запишем решение покороче:

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

19 thoughts on “Умножение и деление целых чисел”

Потому что если, к примеру, два, четыре, шесть минусов, то они всегда будут доават плюс. Т. Е в ответе всегда будет +.
А если три минуса, пять, семь, то в ответе будет —

я внимательно ещё раз посмотрел на выражение и всё понял почему именно так, спасибо за ваши уроки они очень помогают.

Сппсибо за ваши уроки. Но примеры по теме деление и умножение отрицательных чисел не очень убедительны, я так и смог представить как это какое либо число, например (-2) взять по (-2) раза. И у вас противоречие в формулировках, вы говорили, что если есть знак +, то всегда идет смещение правее, но в выражени (-2)+(-5)=-7, смещение по координатной прямой происходил влево

В некоторых задачах перемножаются отрицательные числа, где принцип работы умножения такой же, как и в случае с положительными числами. Подробнее в простейших задачах по математике.

Да, опечатка была. Спасибо, исправил

Попытался представить варажение (-4)*(-2)=8 на координатной прямой, но так и не удалось. Я так понял, что это невозможно представить или я ошибаюсь?

Неплохие у вас уроки в целом, занимаюсь с первого урока.
В некоторых уроках очень трудно информацию сжать для конспекта.

Источник