что такое уменьшить в математике
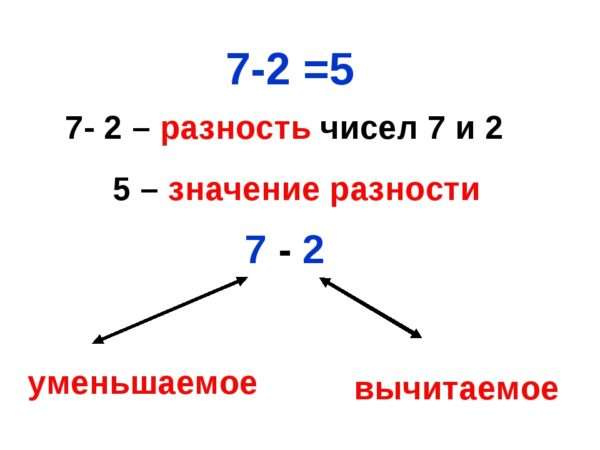
Что такое вычитаемое уменьшаемое и разность: правило
Существуют четыре основных арифметических действия: сложение, вычитание, умножение и деление. Они – основа математики, с их помощью производятся все остальные, более сложные вычисления. Сложение и вычитание – простейшие из них и взаимно противоположны. Но с терминами, используемыми при сложении, мы чаще сталкиваемся в жизни.
Говорим о «сложении усилий» при старании совместно получить нужный результат, о «слагаемых достигнутого успеха» и т.п. Названия же, связанные с вычитанием, остаются в пределах математики, редко появляясь в повседневной речи. Поэтому менее привычны слова вычитаемое, уменьшаемое, разность. Правило нахождения каждого из данных компонентов возможно применить лишь при понимании значения этих названий.
Значение терминов
В отличие от многих научных терминов, имеющих греческое, латинское или арабское происхождение, в данном случае используются слова с русскими корнями. Так что понять их значение несложно, а значит легко и запомнить, что каким термином обозначается.
Что такое разность чисел в математике
Если присмотреться к самому названию, становится заметно, что оно имеет отношение к словам «разный», «разница». Из этого можно заключить, что имеется в виду установленная разница между количествами.
Это интересно! Как раскрыть модуль действительного числа и что это такое
Данное понятие в математике означает:
Обратите внимание! Если количества равны друг другу, то между ними нет разницы. Значит разность их равняется нулю.
Что такое уменьшаемое и вычитаемое
Как следует из названия, уменьшаемое – это то, что делают меньше. А сделать количество меньшим можно, отняв от него часть. Таким образом, уменьшаемым называется число, от которого отнимают часть.
Вычитаемым, соответственно, называется то число, которое от него отнимают.
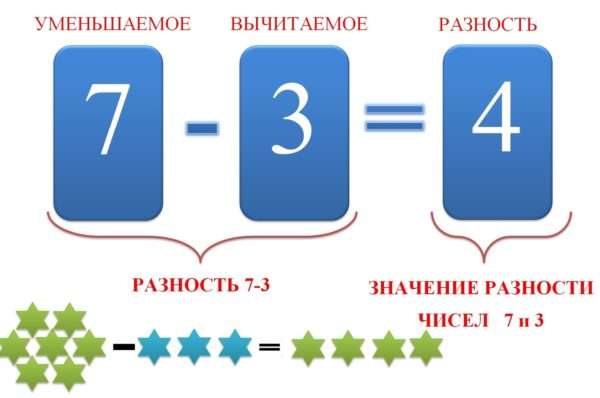
| Уменьшаемое | Вычитаемое | Разность | |
| 18 | 11 | = | 7 |
| 14 | 5 | = | 9 |
| 26 | 22 | = | 4 |
Полезное видео: уменьшаемое, вычитаемое, разность
Правила нахождения неизвестного элемента
Разобравшись в терминах, несложно установить, по какому правилу находится каждый из элементов вычитания.
Поскольку разность – результат данного арифметического действия, то ее и находят с помощью этого действия, никаких других правил тут не требуется. Но они есть на случай, если неизвестен другой член математического выражения.
Это интересно! Уроки математики: умножение на ноль главное правило
Как найти уменьшаемое
Данным термином, как было выяснено, называют количество, из которого вычли часть. Но если одну вычли, а другая осталась в итоге, следовательно, из этих двух частей число и состоит. Получается, что найти неизвестное уменьшаемое можно, сложив два известных элемента.
Итак, в данном случае, чтобы найти неизвестное, следует выполнить сложение вычитаемого и разности:
| ? | – | 11 | = | 7 |
Искомое находится путем сложения известных элементов:
| 7 | + | 11 | = | 18 |
Так же и во всех подобных случаях:
| ? | – | 5 | = | 9 |
| 9 | + | 5 | = | 14 |
| ? | – | 22 | = | 4 |
| 4 | + | 22 | = | 26 |
Как найти вычитаемое
Если целое состоит из двух частей (в данном случае количеств), то при вычитании одной из них в результате получится вторая. Таким образом, чтобы найти неизвестное вычитаемое, достаточно вместо него вычесть из целого разность.
| 18 | – | ? | = | 7 |
Из примера видно, что от 18 отняли некоторую величину, и осталось 7. Чтобы найти эту величину, надо от 18 отнять 7.
| 18 | – | 7 | = | 11 |
По тому же правилу решаются и другие подобные примеры.
| 14 | – | ? | = | 9 |
| 14 | – | 9 | = | 5 |
| 26 | – | ? | = | 4 |
| 26 | – | 4 | = | 22 |
Таким образом, зная точное значение названий, можно легко догадаться, по какому правилу следует искать каждый неизвестный элемент.
Это интересно! Как разложить на множители квадратный трехчлен: формула
Полезное видео: как найти неизвестное уменьшаемое
Вывод
Четыре основных арифметических действия – та база, на которой основываются все математические вычисления, от простых до самых сложных. Конечно, в наше время, когда люди стремятся перепоручить технике все вплоть до мыслительного процесса, привычнее и быстрее производить вычисления с помощью калькулятора. Но любое умение увеличивает независимость человека – от технических средств, от окружающих. Не обязательно делать математику своей специальностью, но обладать хотя бы минимальными знаниями и умениями – значит иметь дополнительную опору для собственной уверенности.
Математика. 1 класс
Конспект урока
Математика, 1 класс
Урок № 35. Уменьшаемое. Вычитаемое. Разность. Использование этих терминов при чтении записей
Перечень вопросов, рассматриваемых в теме:
Вычитание – действие обратное сложению.
Уменьшаемое – число, из которого вычитают.
Вычитаемое – число, которое вычитают.
Разность – результат вычитания.
Слагаемое – число, которое складывают.
Сумма – результат сложения.
Обязательная литература и дополнительная литература:
Теоретический материал для самостоятельного изучения
Давайте решим задачу. В гараже стояли 5 машин. 2 машины уехали. Сколько машин осталось в гараже?
Для решения задачи выберем действие вычитание. Так как машины уехали, их стало меньше.
Ответ: 3 машины в гараже.
Как называются числа при вычитании?
Первое число 8 – число, из которого вычитают. Это уменьшаемое.
Второе число 5 – число, которое вычитают. Это вычитаемое.
Третье число 3 – результат вычитания. Это разность.
Выражение 8 – 5 тоже называется разность.
Равенство 8 – 5 = 3 можно прочитать так. Уменьшаемое – 8, вычитаемое – 5. Разность – 3. Или, разность восьми и пяти равна трем.
Назовем числа при вычитании.
6 – уменьшаемое, 2 – вычитаемое, 4 – разность. Выражение 6 – 2 тоже разность.
Соединим предложение с математической записью.
Уменьшаемое – 9, вычитаемое – 6. 8 – 3
Вычитаемое – 3, уменьшаемое – 8. 7 – 2
Разность чисел 7 и 2. 9 – 6
В коробке было 10 карандашей. Взяли 4 карандаша. Сколько карандашей осталось в коробке.
Для решения задачи выберем действие вычитание. Запишем разность чисел.
Ответ: 6 карандашей.
Ответим на вопросы, поставленные в начале урока.
Числа при вычитании называются уменьшаемое, вычитаемое, разность.
Уменьшаемое – число, из которого вычитают. Вычитаемое – число, которое вычитают. Разность – результат вычитания.
Выражение на вычитание можно читать по-разному. Например, 8 – 1 = 7
Уменьшаемое – 8, вычитаемое – 1, разность – 7. Или, разность чисел 8 и 1 равна 7.
Выполним несколько тренировочных заданий.
а) Вычитаемое – 3. Уменьшаемое – 5.
б) Разность чисел 7 и 2.
в) Сумма чисел 5 и 4.
Вычитание чисел
Вычитание чисел — это арифметическое действие, с помощью которого от единиц одного числа отнимают столько единиц, сколько их содержится в другом числе.
Пример. На столе лежало 9 конфет, 5 из них съели. Сколько конфет осталось на столе?
Чтобы ответить на этот вопрос, надо из общего количества конфет вычесть количество конфет, которые были съедены:
Отнимая 5 раз по одной конфете от общего количества конфет, мы получим количество конфет, которые остались лежать на столе, то есть 4.
Вычесть – значит от одного числа отнять столько единиц, сколько их содержится в другом.
Эта запись означает, что от 9 надо отнять пять. Справа от записи вычитания ставится знак = (равно), после которого записывается полученный результат:
Уменьшаемое, вычитаемое и разность
Уменьшаемое — это число, из которого вычитают. Вычитаемое — это число, которое вычитают. Например, в записи:
9 — это уменьшаемое, 4 — вычитаемое.
Разность (остаток) — это число, которое получается в результате вычитания. Например, в записи:
Вычитание – это арифметическое действие обратное сложению, с помощью которого по сумме и одному слагаемому находится другое слагаемое.
Проверка вычитания
где 15 — это уменьшаемое, 7 — это вычитаемое, а 8 — разность. Чтобы узнать правильно ли было выполнено вычитание, можно:
Общее представление о вычитании натуральных чисел
В рамках это материала мы разберемся с таким действием, как вычитание. Для начала мы попробуем дать общее представление о нем, пояснить сам смысл процесса вычитания. Потом введем и поясним необходимые обозначения и определения. В финальной части мы укажем, в решении каких задач нам может потребоваться вычитание.
Общий смысл процесса вычитания
Само по себе вычитание связано с разъединением некого множества на отдельные части. В этом смысле оно обратно сложению, которое, напротив, объединяет их (см. материал о сложении натуральных чисел).
Что конкретно это означает на практике?
Допустим, у нас есть некоторое количество шаров в вазе. Заберем из всей кучи один-два и положим в другое место. Тем самым мы совершили процесс вычитания, т.е. отняли от множества несколько предметов. То есть суть процесса вычитания состоит именно в исключении, отделении одних предметов от других.
Вернемся к сложению. Мы складываем одни числа с другими для того, чтобы получить сведения об их общем, суммарном количестве. А для чего мы вычитаем? Есть два подхода к пониманию сути этого процесса. От того, какой мы используем, будет зависеть смысл, придаваемый вычитаемому числу.
Для натуральных чисел результат вычитания говорит нам:
1) о том, сколько предметов останется, если убрать из их множества некое определенное количество;
2) о том, сколько нужно убрать предметов из заданного множества, чтобы получить требуемое количество.
Разберем сначала первый случай.
А во втором случае мы узнаем:
Ответ: 4
В этом смысле процесс вычитания натуральных чисел имеет смысл только тогда, когда вычитаемое число меньше, чем уменьшаемое. В самом деле, как можно убрать больше, чем у нас уже есть? В дальнейшем мы останемся в рамках этого ограничения, пока говорим о действиях с натуральными числами.
В результате вычитания у нас, разумеется, может получиться не только другое натуральное число, но и нуль, который говорит о полном отсутствии предметов. Это происходит тогда, когда уменьшаемое и вычитаемое равны. Получается, если мы уберем все предметы, которые у нас есть, то на столе не останется ни одного.
Основные понятия, связанные с вычитанием
Здесь мы укажем общепринятые обозначения и поясним их.
Выше мы уже использовали термины «уменьшаемое» и «вычитаемое». Легко понять, что они означают:
Уменьшаемое – это то, из чего вычитают, вычитаемое – то, которое вычитают.
Когда требуется определить, что получится в результате вычитания одного числа из другого, используются выражения: «вычислить разность», «найти разность», «вычесть одно число из другого», «отнять от одного числа другое».
Таким образом, весь процесс вычитания мы можем представить так: уменьшаемое минус вычитаемое равно разность.
Для решения каких задач нужно знать вычитание
С помощью вычитания можно решить широкий спектр задач. Перечислим их:
1. Найти количество предметов, которое получится после разбиения всего их множества на два других. Примером такой задачи может стать задача с шарами на столе, которую мы приводили в пункте о смысле процесса вычитания. Задачи с нахождением числа предметов, которое надо убрать из имеющегося множества, так же относятся в этому виду.
2. Решить задачи, в которых изменяются значения длины, объема, массы, времени и других измерений.
3. Узнать разницу между количеством предметов, которые входят в два разных множества, или разницу между двумя любыми величинами (скоростями, массами и др.)
Ответ: 10.
Возьмем пример с более сложными числами: