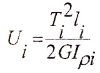что такое угол закручивания
Тема 2.4. Кручение
Под кручением понимается такой вид деформации, когда в поперечных сечениях бруса действует только крутящий момент Mk, (другое обозначение T, Mz), а остальные силовые факторы (нормальная и поперечная силы и изгибающие моменты) отсутствуют.
Или другое определение кручением называют деформацию, возникающую при действии на стержень пары сил, расположенной в плоскости, перпендикулярной к его оси (рис.1).
Кручение возникает в валах, винтовых пружинах, в элементах пространственных конструкций и т.п.
Деформация кручения наблюдается если прямой брус нагружен внешними моментами (парами сил M), плоскости действия которых перпендикулярны к его продольной оси
В чистом виде деформация кручения встречается редко, обычно присутствуют и другие внутренние силовые факторы (изгибающие моменты, продольные силы).
Стержни круглого или кольцевого сечения, работающие на кручение, называют валами.
Внешние крутящие моменты передаются на вал в местах посадки на него шкивов, зубчатых колес, там, где поперечная нагрузка смещена относительно оси вала.
Мы будем рассматривать прямой брус только в состоянии покоя или равномерного вращения. В этом случае алгебраическая сумма всех внешних скручивающих моментов, приложенных к брусу, будет равна нулю.
При расчете брусьев, испытывающий деформацию кручения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от Mk), возникающих в брусе, и нахождение угловых перемещений в зависимости от внешних скручивающих моментов.
При расчете валов обычно бывает известна мощность, передаваемая на вал, а величины внешних скручивающих моментов, подлежат определению. Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п.
§2. Построение эпюр крутящих моментов
Для определения напряжений и деформаций вала необходимо знать значения внутренних крутящих моментов Mk (Mz) в поперечных сечениях по длине вала. Диаграмму, показывающую распределение значений крутящих моментов по длине бруса, называют эпюрой крутящих моментов. Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала.
В простейшем случае, когда вал нагружен только двумя внешними моментами (эти моменты из условия равновесия вала ΣMz=0 всегда равны друг другу по величине и направлены в противоположные стороны), как показано на рис. 1, крутящий момент Mz в любом поперечном сечении вала (на участке между внешними моментами) по величине равен внешнему моменту |M1|=|M2|.
угол закручивания
угол закручивания
Угловая величина относительного поворота полумуфт в окружном направлении под нагрузкой крутящим моментом.
[ГОСТ Р 50371-92]
Тематики
Смотреть что такое «угол закручивания» в других словарях:
относительный угол закручивания — Угол закручивания, приходящийся на единицу длины. [http://www.isopromat.ru/sopromat/terms] Тематики строительная механика, сопротивление материалов EN angle of twist per unit length … Справочник технического переводчика
Кручение — I Кручение (в сопротивлении материалов) вид деформации, характеризующийся взаимным поворотом поперечных сечений стержня, вала и т. д. под влиянием моментов (пар сил), действующих в этих сечениях. Поперечные сечения круглых стержней… … Большая советская энциклопедия
КРУЧЕНИЕ — деформация, возникающая в стержне при приложении к его концу (торцу) системы сил, к рая приводится к паре сил с вектором момента вдоль оси стержня, т. е. к крутящему моменту. Для стержня круглого сечения радиуса а используется гипотеза плоских… … Физическая энциклопедия
Кручение (в сопротивлении материалов) — Кручение (в сопротивлении материалов), вид деформации, характеризующийся взаимным поворотом поперечных сечений стержня, вала и т. д. под влиянием моментов (пар сил), действующих в этих сечениях. Поперечные сечения круглых стержней (валов) при К.… … Большая советская энциклопедия
Кручение — [torsion, twisting] 1. Вид деформации, характеризующийся взаимным поворотом поперечных сечений закрепленного стержня (прутка), вала и т.д. под влиянием моментов (пар сил), действующих в этих сечениях. Поперечные сечения круглых стержней (прутков) … Энциклопедический словарь по металлургии
Кручение — один из видов деформации тел. Проволока, вытянутая вертикально грузом, подвешенным на одном ее конце, тогда как другой ее конец закреплен в неподвижной подставке, и закручивающаяся при вращении упомянутого груза представляет один из примеров… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Кручение (деформация) — У этого термина существуют и другие значения, см. Кручение. Пример деформации кручения цилиндрического стержня … Википедия
ЖЁСТКОСТЬ — мера податливости тела деформации при заданном типе нагрузки: чем больше Ж., тем меньше деформация. В сопротивлении материалов и теории упругости Ж. характеризуется коэффициентом (или суммарным внутр. усилием) и характерной деформацией упругого… … Физическая энциклопедия
Основания сооружений — массивы горных пород, непосредственно воспринимающие нагрузки от сооружений. В О. с. возникают деформации от нагружения их сооружениями. О. с. могут служить все виды горных пород: скальные (скальные О. с.) и рыхлые (грунтовые О. с., см.… … Большая советская энциклопедия
ТЯГОТЕНИЕ — или гравитация, свойство материи, которое состоит в том, что между любыми двумя частицами существуют силы притяжения. Тяготение универсальное взаимодействие, охватывающее всю доступную наблюдению Вселенную и потому называемое всемирным. Как мы… … Энциклопедия Кольера
ПроСопромат.ру
Технический портал, посвященный Сопромату и истории его создания
Кручение
Внутренний крутящий момент в сечении вала Мк (может быть обозначен буквой Т, Мz) вычисляется с помощью метода сечений, при этом моменты учитываются по одну сторону от сечения.
где Мi – внешний активный или реактивный крутящий момент; правило знаков для внутренних крутящих моментов устанавливается произвольно.
Для вала с круглым (в т.ч. в виде кольца) поперечным сечением касательные напряжения определяются по формуле:
Максимальные касательные напряжения действуют в точках поверхностного слоя при ρ=ρmax
Условие прочности по допускаемым напряжениям
где — 
это допускаемое касательное напряжение.
Угол закручивания (рад) на силовом участке вала при постоянных значениях крутящего момента и поперечного момента инерции для данного участка вычисляется следующим образом
где G – модуль сдвига
Относительный угол закручивания (рад/м) для силового участка
Условие жесткости при кручении вала с круглым поперечным сечением записывается в виде
Для вала с прямоугольным поперечным сечением эпюры касательных напряжений имеют вид.
В характерных точках сечения
угол закручивания на силовом участке вала
Если вал с эллиптической формой поперечного сечения и полуосями a и b, то его характерные эпюры касательных напряжений будут выглядеть следующим образом.
Касательные напряжения в характерных точках сечения
Угол закручивания на силовом участке вала
Кручение бруса тонкостенного замкнутого круглого сечения
Тонкостенное круглое сечение характеризуется средним радиусом Rср и толщиной стенки трубы δ:
Считается, что касательные напряжения по толщине стенки распределяются равномерно и равны:
Угол закручивания
Кручение пустотелых валов круглого сечения
Трубчатое сечение бруса в условиях кручения оказывается наиболее рациональным, так как материал из центральной зоны сечения, слабо напряженной, удален в область наибольших касательных напряжений. Вследствие этого прочностные свойства материала используются значительно полнее, чем в брусьях сплошного круглого сечения, и при всех прочих равных условиях применение трубчатого сечения вместо сплошного позволяет экономить материал.
Теория расчета бруса сплошного круглого сечения полностью применима и к пустотелым валам. Изменяются лишь геометрические характеристики сечения:
Кручение бруса прямоугольного сечения
Опыт показывает, что при кручении брусьев некруглого поперечного сечения сами сечения не остаются плоскими, то есть происходит депланация поперечных сечений. Исследовать напряженное и деформированное состояние таких брусьев при кручении методами сопротивления материалов не представляется возможным, так как в основе их лежит гипотеза плоских сечений (гипотеза Бернулли).
Задача о кручении бруса некруглого, в частности, прямоугольного сечения решена с помощью метода теории упругости, и на основе этого решения предложены простые расчетные формулы, имеющие ту же структуру, что и формулы для бруса круглого сечения, а именно:
Здесь: Wк=α∙h∙b2– момент сопротивления при кручении,
Iк=β∙h∙b3 – момент инерции при кручении.
В этих формулах: b – меньшая из сторон прямоугольника,
h – большая сторона,
α, β – коэффициенты, значения которых приводятся в таблице в зависимости от отношения сторон h/b (эта таблица содержится в рубрике «Кручение» или в любом учебнике сопротивления материалов).
Распределение касательных напряжений по прямоугольному сечению тоже отличается от распределения в круглом сечении:
Значения коэффициента γ Запись опубликована 04.09.2014 автором admin в рубрике Кручение, Сопромат.
iSopromat.ru
Кручением называется такой вид деформации бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент T.
Брусья, испытывающие кручение, принято называть валами.
Внутренний крутящий момент
Внутренние скручивающие моменты появляются под действием внешних крутящих моментов mi, расположенных в плоскостях, перпендикулярных к продольной оси бруса.
Скручивающие моменты передаются на вал в местах посадки зубчатых колес, шкивов ременных передач и т.п.
Величина крутящего момента в любом сечении вала определяется методом сечений: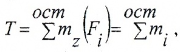 
т.е. крутящий момент численно равен алгебраической сумме скручивающих моментов mi, расположенных по одну сторону от рассматриваемого сечения.
Правило знаков внутренних скручивающих моментов:
Положительными принимаются внутренние моменты, стремящиеся повернуть рассматриваемую часть вала против хода часовой стрелки, при рассмотрении со стороны отброшенной части вала.
В технике наиболее широко используются валы круглого поперечного сечения.
Теория кручения круглых валов основана на следующих гипотезах:
Напряжения при кручении
В поперечных сечениях вала при кручении имеют место только касательные напряжения.
Касательные напряжения, направленные перпендикулярно к радиусам, для произвольной точки, отстоящей на расстоянии ρ от центра, вычисляются по формуле: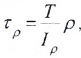 
где Iρ — полярный момент инерции.
Эпюра касательных напряжений при кручении имеет следующий вид: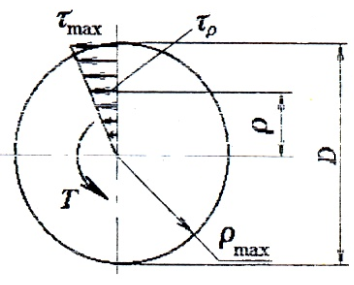 
Касательные напряжения меняются по линейному закону и достигают максимального значения на контуре сечения при ρ= ρmax: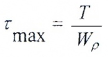 
Здесь: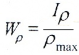 
— полярный момент сопротивления.
Геометрические характеристики сечений:
а) для полого вала: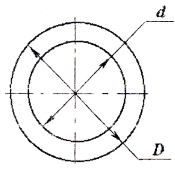 
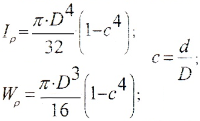
б) для вала сплошного сечения (c=0)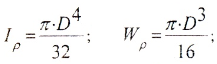 
в) для тонкостенной трубы (t 0,9)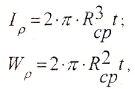 
где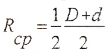 
— радиус срединной поверхности трубы.
Деформации
Деформации валов при кручении заключаются в повороте одного сечения относительно другого.
Угол закручивания вала на длине Z определяется по формуле: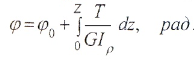 
Если крутящий момент и величина GIρ, называемая жесткостью поперечного сечения при кручении, постоянны, для участка вала длиной l имеем: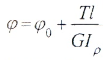 
Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания: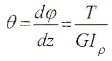 
Расчет валов сводится к одновременному выполнению двух условий:
Для стальных валов принимается:
Используя условия прочности и жесткости, как и при растяжении – сжатии можно решать три типа задач:
Из двух найденных значений крутящего момента необходимо принять меньшее.
Потенциальная энергия упругой деформации определяется по формуле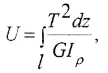 
или для участка вала при постоянном T и GIρ 
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
ПроСопромат.ру
Технический портал, посвященный Сопромату и истории его создания
Архив рубрики: Кручение
Статически неопределимые задачи при кручении
Рассмотрим схему нагружения, по которой оба конца вала защемлены и подвергаются действию кручения. Следует определить усилия в защемлениях МА и МВ и построить эпюры крутящих моментов и углов закручивания.
Сумма моментов относительно оси: 
(1)
Для решения уравнения (1) выбираем основную систему (рис.б.). Под основной системой понимают статически определимую, но геометрически неизменяемую систему. К основной системе прикладывают неизвестные усилия МА, МВ и заданный момент М. Эта система вместе с дополнительным уравнением совместности деформаций является системой, эквивалентной заданной (рис.в.). Запишем дополнительное уравнение совместности деформаций, которое обусловлено тем, что угол закручивания в защемлении равен нулю:
(2)
Распишем выражение (2):
тогда имеем: 
(3) В знаменателях — жесткость вала при кручении — произведение модуля сдвига на полярный момент инерции.
Из (3) определим МВ и подставим в уравнение (1). Статическая неопределимость раскрыта и далее можно строить эпюры.
Геометрические характеристики, применяемые при кручении
Рассмотрим сплошное и трубчатое сечения:
Для сплошного сечения:
полярный момент инерции сечения 
полярный момент сопротивления сечения
Для трубчатого сечения:
полярный момент инерции сечения 
полярный момент сопротивления сечения
, где коэффициент
(может обозначаться как «с», «к» и др.)
Три типа задач при расчете на жесткость при кручении:
Типы задач при расчете на жесткость при кручении:
1. Проверочный расчет: максимальный относительный угол закручивания должен быть меньше или равным допускаемому.
Мz – крутящий момент, G –это модуль сдвига.
2. Проектный расчет
Из условия жесткости подбор сечения (определяем полярный момент инерции сечения):
Для круглого сечения:
или при переходе к градусной мере:
3. Определение допускаемого крутящего момента
Допускаемый крутящий момент из условия жесткости:
Расчеты на жесткость при кручении
В ряде случаев вал должен удовлетворять не только условиям прочности, но и условиям жесткости.
Условие жесткости при кручении: максимальный относительный угол закручивания должен быть меньше или равным допускаемому.
Допускаемый относительный угол закручивания 
зависит от назначения вала.
Три типа задач при расчете на прочность при кручении
Расчет на прочность при кручении.Типы задач при расчете на прочность при кручении:
1. Проверочный расчет:
2. Проектный расчет
Для круглого сечения:
Для кольцевого сечения:
3. Определение допускаемого крутящего момента
Расчеты на прочность при кручении
Теория кручения используется в основном при расчете валов машин и механизмов.
Введем понятие такой геометрической характеристики как полярный момент сопротивления сечения:
Единица измерения полярных моментов сопротивления сечения — кубические см,м и т.д.
Формула для определения касательных напряжений при кручении в любой точке сечения:
Тогда условие прочности при кручении:
В качестве внутреннего силового фактора используется крутящий момент, в качестве геометрической характеристики – полярный момент сопротивления сечения.
Допускаемое напряжение стали на сдвиг принимается 
, где 
— допускаемое напряжение на растяжение. Но, поскольку валы помимо кручения работают на изгиб, то в ориентировочных расчетах это учитывают введением пониженного допускаемого напряжения 
.
Полярные моменты сопротивления сечения:
Для круга:
Для кольца:
Предпосылки теории кручения
В основу технической теории о кручении положена гипотеза плоских сечений и допущения:
1. Расстояния между поперечными сечениями в процессе деформации не меняются, т.е. длина бруса остается постоянной.
2. Радиусы поперечных сечений не искривляются.
Все это подтверждается экспериментально, а также выводами теории упругости (кроме допущения о непрерывности).
Напряжения и деформации при кручении круглого бруса
Из исследований известно, что характер деформирования в значительной степени зависит от формы поперечного сечения. В технике чаще всего применяются стержни круглого и кольцевого сечения. Рассмотрим стержень круглого сечения.
В поперечном сечении возникают только касательные напряжения. Нормальные силы параллельны оси z и не дают момента. Таким образом, в качестве внутреннего силового фактора имеется только крутящий момент – результирующий момент внутренних касательных сил τdА, действующих на площадке dА.
В интегральном виде крутящий момент можно представить как:
(1), где ρ – плечо элементарной силы относительно точки 0 – центра сечения.
Формула (1) выражает статическую сторону задачи о кручении, но не позволяет определить значение касательного напряжения τ, пока неизвестен закон распределения касательных напряжений по сечению.
В основу технической теории о кручении положена гипотеза плоских сечений и допущения:
1. Расстояния между поперечными сечениями в процессе деформации не меняются, т.е. длина бруса остается постоянной.
2. Радиусы поперечных сечений не искривляются.
Все это подтверждается экспериментально, а также выводами теории упругости (кроме допущения о непрерывности).
Выделим из бруса трубчатый стержень с внутренним радиусом ρ и бесконечно малой толщиной dρ – тогда касательные напряжения можно считать равномерно распределенными по кольцевому сечению.
Мерой деформации при кручении является угол закручивания:
(2) – относительный угол закручивания, где
dφ- угол взаимного поворота двух бесконечно близких сечений.
dz – расстояние между ними.
Следует отметить, что у относительного угла закручивания θ в кручении такая же роль, как у ε (относительная продольная деформация) при растяжении (сжатии). Если рассмотреть деформацию на трубчатом стержне, то можно увидеть, что СВ перешло в СВ’, ЕD — ЕD’, ОВ — ОВ’, ОD — ОD’. Таким образом, можно констатировать, что бесконечно малый элемент боковой поверхности СВДЕ претерпевает чистый сдвиг. Тогда угол сдвига:
(3) Эта формула выражает геометрическую сторону задачи.
Теперь обратимся к физической стороне задачи. Известен закон Гука для сдвига:
Согласно принятым допущениям величина θ является одинаковой для всех трубчатых стержней, из которых может быть составлен круглый брус. G – модуль сдвига тоже величина постоянная, следовательно, закон распределения касательных напряжений линеен и находится в зависимости от расстояния ρ.
Gθ=const, поэтому вынесены за знак интеграла, а в подынтегральном выражении наблюдается полярный момент инерции сечения, таким образом получаем:
, откуда выразим относительный угол закручивания:
(5)
Формулу (5) подставим в (4) и получим формулу для определения касательных напряжений при кручении в любой точке сечения:
Из формулы (6) видно, что касательные напряжения τ возрастают от 0 (центр) до max в точках внешнего контура. Максимальное напряжение:
По углу закручивания θ легко определить абсолютный угол поворота одного сечения относительно другого. Из формул (2) и (5):
, где ℓ- расстояние между сечениями.
Если брус одинаков по сечению по длине (Iρ=const), и крутящий момент постоянен, то после интегрирования получим значение угла поворота в радианах:
Жесткость сечения при сдвиге. В знаменателе произведение модуля сдвига на полярный момент инерции 
называется жесткостью сечения при сдвиге.
Определение крутящего момента через мощность.
На практике мощность чаще всего задаётся либо в киловаттах, либо лошадиных силах и числом оборотов в минуту.
Кручение
Внутренний крутящий момент в сечении вала Мк (может быть обозначен буквой Т, Мz) вычисляется с помощью метода сечений, при этом моменты учитываются по одну сторону от сечения.
где Мi – внешний активный или реактивный крутящий момент; правило знаков для внутренних крутящих моментов устанавливается произвольно.
Для вала с круглым (в т.ч. в виде кольца) поперечным сечением касательные напряжения определяются по формуле:
Максимальные касательные напряжения действуют в точках поверхностного слоя при ρ=ρmax
Условие прочности по допускаемым напряжениям
где — это допускаемое касательное напряжение.
Угол закручивания (рад) на силовом участке вала при постоянных значениях крутящего момента и поперечного момента инерции для данного участка вычисляется следующим образом
где G – модуль сдвига
Относительный угол закручивания (рад/м) для силового участка
Условие жесткости при кручении вала с круглым поперечным сечением записывается в виде
Для вала с прямоугольным поперечным сечением эпюры касательных напряжений имеют вид.
В характерных точках сечения
угол закручивания на силовом участке вала
Если вал с эллиптической формой поперечного сечения и полуосями a и b, то его характерные эпюры касательных напряжений будут выглядеть следующим образом.
Касательные напряжения в характерных точках сечения
Угол закручивания на силовом участке вала
Кручение бруса тонкостенного замкнутого круглого сечения
Тонкостенное круглое сечение характеризуется средним радиусом Rср и толщиной стенки трубы δ:
Считается, что касательные напряжения по толщине стенки распределяются равномерно и равны:
Угол закручивания
Кручение пустотелых валов круглого сечения
Трубчатое сечение бруса в условиях кручения оказывается наиболее рациональным, так как материал из центральной зоны сечения, слабо напряженной, удален в область наибольших касательных напряжений. Вследствие этого прочностные свойства материала используются значительно полнее, чем в брусьях сплошного круглого сечения, и при всех прочих равных условиях применение трубчатого сечения вместо сплошного позволяет экономить материал.
Теория расчета бруса сплошного круглого сечения полностью применима и к пустотелым валам. Изменяются лишь геометрические характеристики сечения:
Кручение бруса прямоугольного сечения
Опыт показывает, что при кручении брусьев некруглого поперечного сечения сами сечения не остаются плоскими, то есть происходит депланация поперечных сечений. Исследовать напряженное и деформированное состояние таких брусьев при кручении методами сопротивления материалов не представляется возможным, так как в основе их лежит гипотеза плоских сечений (гипотеза Бернулли).
Задача о кручении бруса некруглого, в частности, прямоугольного сечения решена с помощью метода теории упругости, и на основе этого решения предложены простые расчетные формулы, имеющие ту же структуру, что и формулы для бруса круглого сечения, а именно:
Здесь: Wк=α∙h∙b2– момент сопротивления при кручении,
Iк=β∙h∙b3 – момент инерции при кручении.
В этих формулах: b – меньшая из сторон прямоугольника,
h – большая сторона,
α, β – коэффициенты, значения которых приводятся в таблице в зависимости от отношения сторон h/b (эта таблица содержится в рубрике «Кручение» или в любом учебнике сопротивления материалов).
Распределение касательных напряжений по прямоугольному сечению тоже отличается от распределения в круглом сечении:
Значения коэффициента γ Запись опубликована 04.09.2014 автором admin в рубрике Кручение, Сопромат.