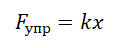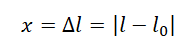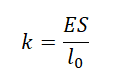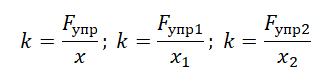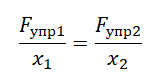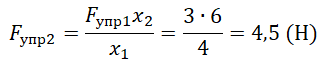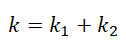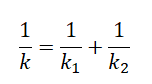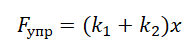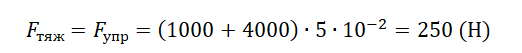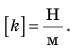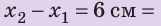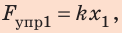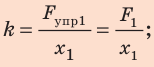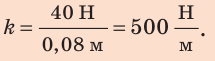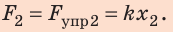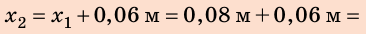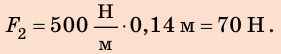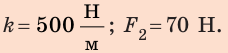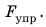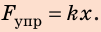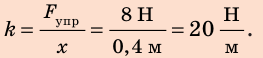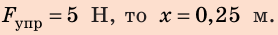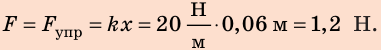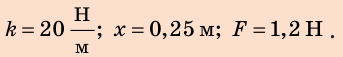что такое удлинение в физике

Сила упругости

Сила упругости широко используется в технике. Эта сила возникает в упругих телах при их деформации. Деформация – это изменение формы тела, под действием приложенных сил.

Виды деформации

Деформация – это изменение формы, или размеров тела.

Есть несколько видов деформации:

Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.

Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.

Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б – эта же линейка, деформируемая кручением.

В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.

Растяжение пружины

Рассмотрим подробнее деформацию растяжения на примере пружины.

Давайте прикрепим пружину к некоторой поверхности (рис. 2). На рисунке слева указана начальная длина \(L_<0>\) пружины.

Подвесим теперь к пружине груз. Пружина будет иметь длину \(L\), указанную на рисунке справа.

Сравним длину нагруженной пружины с длиной свободно висящей пружины.

\[ \large L_ <0>+ \Delta L = L \]

Найдем разницу (разность) между длинами свободно висящей пружины и пружины с грузом. Вычтем для этого из обеих частей этого уравнения величину \(L_<0>\).

\( L_ <0>\left(\text <м>\right) \) – начальная длина пружины;

\( L \left(\text <м>\right) \) – конечная длина растянутой пружины;

\( \Delta L \left(\text <м>\right) \) – кусочек длины, на который растянули пружину;

Величину \( \Delta L \) называют удлинением пружины.

Иногда рассчитывают относительное удлинение. Это относительное удлинение часто выражают десятичной дробью. Или дробью, в знаменателе которой находится число 100 — такую дробь называют процентом.

Примечание: Отношение – это дробь. Относительное – значит, дробное.

\( \varepsilon \) – это отношение (доля) растяжения пружины к ее начальной длине. Измеряют в процентах и называют относительным удлинением.

Расчет силы упругости

Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.

Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.

Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.

Закон Гука

Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал \( F_<\text<упр>> \) силой упругости.

\[ \large \boxed< F_<\text<упр>> = k \cdot \Delta L >\]

Эту формулу назвали законом упругости Гука.

\( F_<\text<упр>> \left( H \right) \) – сила упругости;

\( \Delta L \left(\text <м>\right) \) – удлинение пружины;

\( \displaystyle k \left(\frac<\text<м>> \right) \) – коэффициент жесткости (упругости).

Какие деформации называют малыми

Закон Гука применяют для малых удлинений (деформаций).

Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.

Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.

Как рассчитать коэффициент жесткости

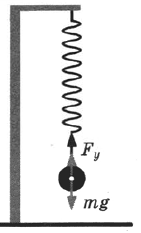
Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.

Так как силы взаимно компенсируются, в правой части уравнения находится ноль.

\[ \large F_<\text<упр>> — m \cdot g = 0 \]

Подставим в это уравнение выражение для силы упругости

\[ \large k \cdot \Delta L — m \cdot g = 0 \]

Прибавим к обеим частям вес груза и разделим на измеренное изменение длины \(\Delta L \) пружины. Получим выражение для коэффициента жесткости:

Соединяем две одинаковые пружины

В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.

Параллельное соединение пружин

На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину \(\Delta L\). Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.

Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом \(mg\).

\[ \large k_ <1>\cdot \Delta L = m \cdot g \]

Две параллельные пружины:

\[ \large k_<\text<параллел>> \cdot \Delta L \cdot \frac<1><2>= m \cdot g \]

Так как правые части уравнений совпадают, левые части тоже будут равны:

\[ \large k_<\text<параллел>> \cdot \Delta L \cdot \frac<1><2>= k_ <1>\cdot \Delta L \]

Обе части уравнения содержат величину \(\Delta L \). Разделим обе части уравнения на нее:

Умножим обе части полученного уравнения на число 2:

Коэффициент жесткости \(k_<\text<параллел>>\) двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной

Последовательное соединение пружин

Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину \(\Delta L\). Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.

Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.

На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину \(\Delta L\).

Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений

Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом \(mg\).

\[ \large k_ <1>\cdot \Delta L = m \cdot g \]

Две последовательные пружины:

\[ \large k_<\text<послед>> \cdot \Delta L \cdot 2 = m \cdot g \]

Так как правые части уравнений совпадают, левые части тоже будут равны:

\[ \large k_<\text<послед>> \cdot \Delta L \cdot 2 = k_ <1>\cdot \Delta L \]

Обе части уравнения содержат величину \(\Delta L \). Разделим обе части уравнения на нее:

Разделим обе части полученного уравнения на число 2:

Коэффициент жесткости \(k_<\text<послед>>\) двух пружин, соединенных последовательно, уменьшится вдвое, в сравнении с одной такой пружиной

Потенциальная энергия сжатой или растянутой пружины

Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину \(\Delta L \) обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу, например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.

Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).

Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:

\[ \large \boxed < E_

= \frac <2>\cdot \left( \Delta L \right)^ <2>>\]

\( E_

\left( \text <Дж>\right)\) – потенциальная энергия сжатой или растянутой пружины;

\( \Delta L \left(\text <м>\right) \) – удлинение пружины;

\( \displaystyle k \left(\frac<\text<м>> \right) \) – коэффициент жесткости (упругости) пружины.

Источник

Сила упругости и закон Гука

теория по физике 🧲 динамика

Сила упругости — сила, которая возникает при деформациях тел в качестве ответной реакции на внешнее воздействие. Сила упругости имеет электромагнитную природу.

Деформация — изменение формы или объема тела.

Сила упругости обозначается как F _упр. Единица измерения — Ньютон (Н). Сила упругости направлена противоположно перемещению частиц при деформации.

Если после окончания действия внешних сил тело возвращает прежние форму и объем, то деформацию и само тело называю упругими. Если после окончания действия внешних сил тело остается деформированным, то деформацию и само тело называют пластическими, или неупругими.

Примеры упругой деформации:

Примеры пластической деформации:

Закон Гука

При упругой деформации есть взаимосвязь между силой упругости, возникающей в результате деформации, и удлинением деформируемого тела. Эту взаимосвязь первым обнаружил английский ученый Роберт Гук.

Модуль силы упругости, возникающей при деформации тела, пропорционален его удлинению.

x — абсолютное удлинение (деформация), k — коэффициент жесткости тела.

Абсолютное удлинение определяется формулой:

l₀ — начальная длина тела, l — длина деформированного тела, ∆l — изменение длины тела.

Коэффициент жесткости тела определяется формулой:

E — модуль упругости (модуль Юнга). Каждое вещество обладает своим модулем упругости. S — площадь сечения тела.

Важно! Закон Гука не работает в случае, если деформация была пластической.

Пример №1. Под действием силы 3Н пружина удлинилась на 4 см. Найти модуль силы, под действием которой удлинение пружины составит 6 см.

Согласно третьему закону Ньютона модуль силы упругости будет равен модулю приложенной к пружине силе. В обоих случаях постоянной величиной окажется только жесткость пружины. Выразим ее из закона Гука и применим к каждому из случаев:

Приравняем правые части формул:

Выразим и вычислим силу упругости, возникающую, когда удлинение пружины составит 6 см:

Если пружину растягивают две противоположные силы, то модули силы упругости и модули этих сил равны между собой:

Если груз подвешен к пружине, сила упругости будет равна силе тяжести, действующей на это тело:

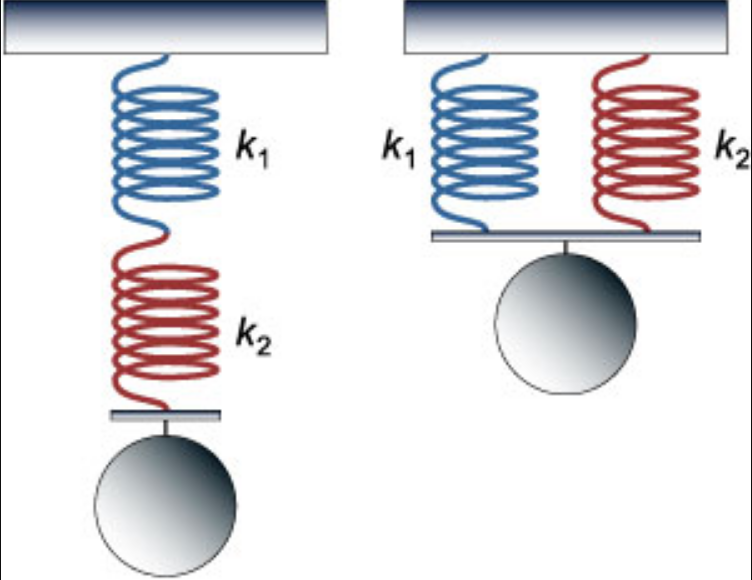
Если пружины соединены параллельно, их суммарный коэффициент жесткости будет равен сумме коэффициентов жесткости каждой из этих пружин:

Если пружины соединены последовательно, их обратное значение суммарного коэффициента жесткости будет равен сумме обратных коэффициентов жесткости для каждой из пружин:

Пример №2. Две пружины соединены параллельно. Жесткость одной из пружин равна 1000 Нм, второй — 4000 Нм. Когда к пружинам подвесили груз, они удлинились на 5 см. Найти силу тяжести груза.

Переведем сантиметры в метры: 5 см = 5∙10 –2 м.

Запишем закон Гука с учетом параллельного соединения пружин:

Модуль силы тяжести согласно третьему закону Ньютона равен модулю силы упругости. Отсюда:

На рисунке представлен график зависимости модуля силы упругости от удлинения пружины. Какова жёсткость пружины?

Источник

Содержание:

Деформация тела:

Вспомните ненастный день: дует порывистый ветер, гнутся деревья. Чем сильнее ветер, тем больше гнутся деревья. А вот физики говорят, что деревья деформируются. Когда ветер стихает, деревья возвращаются в свое первоначальное положение — деформация исчезает. Но если ветер достаточно сильный, то ветви деревьев и даже их стволы могут сломаться.

Виды деформации

Уже отмечалось, что результатом действия силы на тело может быть как изменение скорости движения тела, так и его деформация. Например, если толкнуть мячик, то он придет в движение, а некоторые его части при толчке сместятся относительно друг друга — мячик деформируется.

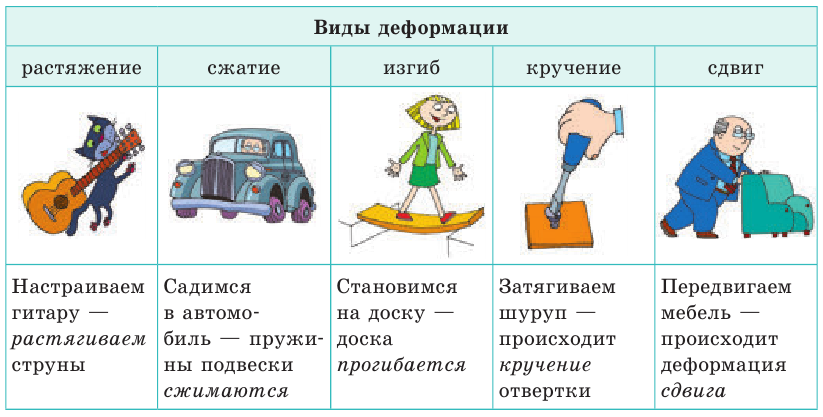
Деформация — изменение формы и (или) размеров тела. В зависимости от того, как именно части тела смещаются относительно друг друга, различают деформации растяжения, сжатия, изгиба, кручения, сдвига (см. таблицу).

Различия упругих и пластических деформаций

Возьмите эспандер (или ластик) и сожмите его — эспандер согнется. Но если прекратить сжимать эспандер, он полностью восстановит свою форму — деформация исчезнет (рис. 19.1). Деформации, которые полностью исчезают после прекращения действия на тело внешних сил, называют упругими.

Делая глиняную фигурку, мастер мнет руками комок глины, и глина сохранит форму, которую придаст ей мастер (рис. 19.2). Тяжелый пресс на монетном дворе чеканит монеты из металлических заготовок, — после прекращения действия пресса монета не восстановит свою прежнюю форму куска металла. И глина, и металл «не помнят» своей формы до деформации и не восстанавливают ее. Деформации, которые сохраняются после прекращения действия на тело внешних сил, называют пластическими. Попробуйте привести другие примеры упругих и пластических деформаций.

Определение силы упругости

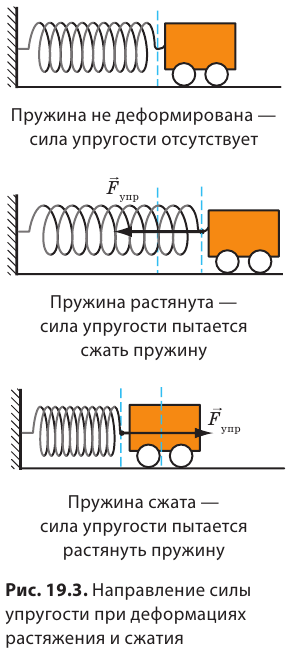
При деформации всегда возникает сила, стремящаяся восстановить то состояние тела, в котором оно находилось до деформации. Эту силу называют силой упругости (рис. 19.3).

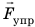
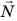
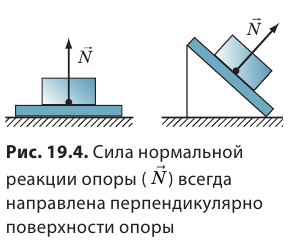
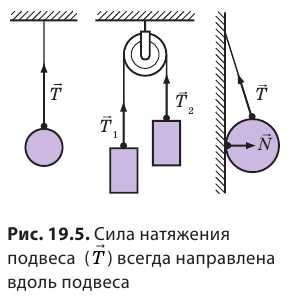
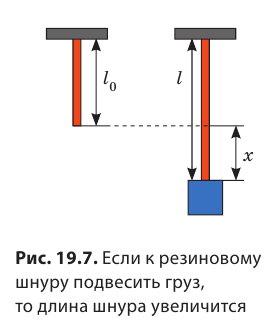
Сила упругости — это сила, которая возникает во время деформации тела и направлена в сторону, противоположную направлению смещения частей этого тела при деформации. Обычно силу упругости обозначают символом , но в некоторых случаях используют и другие символы. Если тело давит на опору, то опора деформируется (прогибается). Деформация опоры вызывает появление силы упругости, действующей на тело перпендикулярно поверхности опоры. Эту сила называют силой нормальной реакции опоры и обозначаются символом (рис. 19.4).

Если тело растягивает подвес (нить, жгут, шнур), то возникает сила упругости, направленная вдоль подвеса. Эту силу называют силой натяжения подвеса и обозначают символом 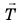(рис. 19.5).

Закон Гука

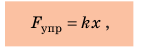
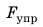
Научное исследование процессов растяжения и сжатия тел начал Роберт Гук (рис. 19.6) в XVII в. Результатом работы ученого стал закон, который позже получил название закон Гука: При малых упругих деформациях растяжения или сжатия сила упругости прямо пропорциональна удлинению тела и всегда пытается вернуть тело в недеформированное состояние: где — сила упругости; x — удлинение тела; k — коэффициент пропорциональности, который называют жесткостью тела.

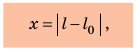
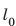
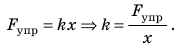
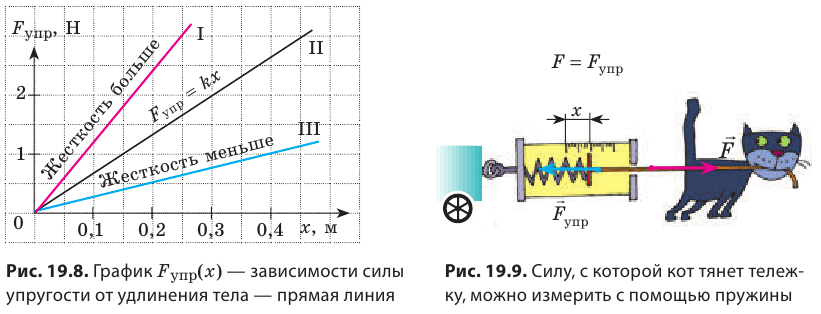
Удлинение — это физическая величина, которая характеризует деформации растяжения и сжатия и равна изменению длины тела в результате деформации. Удлинение х определяется по формуле: где l — длина деформированного тела; — длина недеформированного тела (рис. 19.7). Жесткость тела можно определить, воспользовавшись законом Гука: Единица жесткости в СИ — ньютон на метр:

Жесткость — это характеристика тела, поэтому она не зависит ни от силы упругости, ни от удлинения. Жесткость зависит от формы и размеров тела, а также от материала, из которого тело изготовлено. Сила упругости прямо пропорциональна удлинению тела, поэтому график зависимости 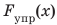— прямая (рис. 19.8). Чем больше жесткость тела, тем выше расположен график. Воспользовавшись графиками на рис. 19.8, определите жесткость тел І–ІІІ и убедитесь в справедливости последнего утверждения.

Почему возникает сила упругости

Вы хорошо знаете, что все тела состоят из частиц (атомов, молекул, ионов). В твердых телах частицы колеблются около положений равновесия и взаимодействуют межмолекулярными силами притяжения и отталкивания. В положениях равновесия данные силы уравновешены. При деформации тела во взаимном расположении его частиц происходят изменения. Если расстояние между частицами увеличивается, то межмолекулярные силы притяжения становятся больше сил отталкивания. Если же частицы сближаются, то больше становятся межмолекулярные силы отталкивания. Другими словами: при деформации частицы «стремятся» вернуться в положение равновесия. Силы, возникающие при изменении положения одной частицы, очень малы. Но когда тело деформируется, изменяется взаимное расположение огромного количества частиц. В результате сложение сил дает заметную равнодействующую, которая противостоит деформации тела. Это и есть сила упругости. Итак, сила упругости — проявление действия межмолекулярных сил.

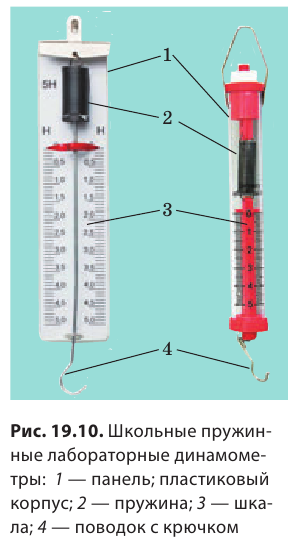
Приборы для измерения силы

Сила — это физическая величина, поэтому ее можно измерить. Приборы для измерения силы называют динамометрами. Основная составляющая простейших динамометров — пружина. Рассмотрим принцип действия таких динамометров на простом примере. Чтобы с помощью пружины, жесткость k которой известна, измерить силу F, с которой кот тянет тележку (рис. 19.9), необходимо:

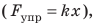
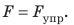
1) измерить удлинение x пружины; 2) воспользовавшись законом Гука, определить силу упругости которая действует на кота со стороны пружины и по значению равна силе F тяги кота: Понятно, что каждый раз измерять удлинение пружины и рассчитывать силу неудобно. Поэтому пружину закрепляют на панели со шкалой, проградуированной в единицах силы. Именно так устроены простейшие школьные лабораторные динамометры (рис. 19.10). Существуют и другие виды пружинных динамометров (см., например, рис. 19.11).

Пример №1

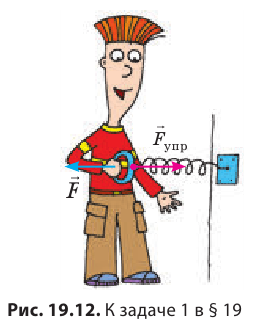
Действуя на пружину силой 40 Н, мальчик растянул ее на 8 см. Определите жесткость пружины. Какую силу нужно приложить мальчику, чтобы растянуть эту пружину еще на 6 см? Деформацию пружины считайте малой упругой. Анализ физической проблемы. Сила, которую прикладывает мальчик, по значению равна силе упругости, возникающей при растяжении пружины: F= уFпр (рис. 19.12). Деформация является малой упругой, поэтому воспользуемся законом Гука. Задачу будем решать в единицах СИ.

,,

,

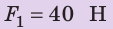
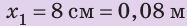
Решение:

1. Вычислим жесткость пружины:

поэтому

2. Найдем силу, которую нужно приложить мальчику, чтобы дополнительно растянуть пружину:

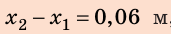
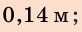
По условию ,поэтому следовательно,

Анализ результатов. Для удлинения пружины на 8 см мальчик прикладывал силу 40 Н; для удлинения пружины еще на 6 см ему нужно увеличить силу на 30 Н — это правдоподобный результат.

Ответ:

Пример №2

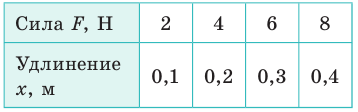
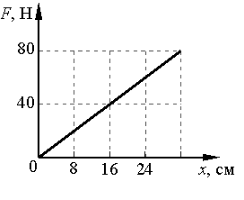
Выполняя экпериментальное задание, девочка увеличивала нагрузку на резиновый шнур. Каждый раз она измеряла силу, действующую на шнур, и соответствующее удлинение шнура. Воспользовавшись таблицей, составленной девочкой, постройте график уFпр(x). С помощью графика определите: 1) жесткость шнура; 2) удлинение шнура, когда к нему приложена сила 5 Н; 3) силу, которую нужно приложить к шнуру, чтобы его удлинение было равно 6 см.

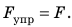
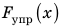
Анализ физической проблемы. При растяжении шнура возникает сила упругости, которая по значению равна силе, действующей на шнур: Для построения графика зависимости начертим две взаимно перпендикулярных оси. На горизонтальной оси будем откладывать удлинение x шнура, а на вертикальной — соответствующее значение силы упругости

Решение:

Построив указанные в таблице точки (см. рисунок), увидим, что все они принадлежат одной прямой, значит, для любой точки графика имеем:

1) Выбрав точку А графика, найдем жесткость шнура:

2) Удлинение шнура в результате действия силы 5 Н найдем по графику: если

3) Силу, которую нужно приложить к шнуру, чтобы его удлинение было равно 0,06 м, найдем по закону Гука:

Ответ:

Итоги:

Деформацией называют изменение формы и (или) размеров тела. Если после прекращения действия на тело внешних сил деформация полностью исчезает, то это упругая деформация; если деформация сохраняется, то это пластическая деформация.

Сила упругости 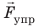— это сила, которая возникает во время деформации тела и направлена в сторону, противоположную направлению смещения частей этого тела при деформации.

Сила упругости — проявление действия межмолекулярных сил. При малых упругих деформациях растяжения и сжатия выполняется закон Гука: сила упругости прямо пропорциональна удлинению тела и всегда пытается вернуть тело в недеформированное состояние: 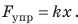Приборы для измерения силы называют динамометрами. Простейшие из них — пружинные динамометры.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник