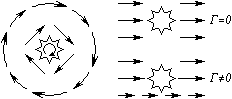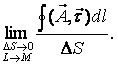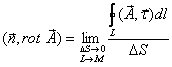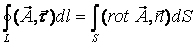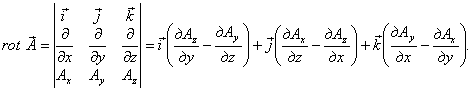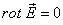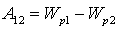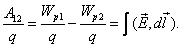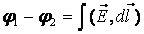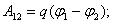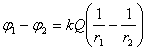Что такое циркуляция вектора напряженности электростатического поля
Циркуляция вектора напряженности электростатического поля



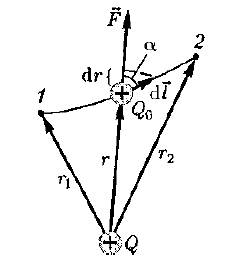
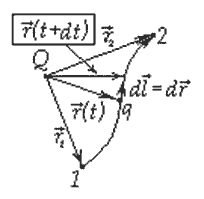
Если в электростатическом поле точечного заряда Q из точки 1 в точку 2 вдоль произвольной траектории перемещается другой точечный заряд Qo, то сила, приложенная к заряду, совершает работу. Работа силы F на элементарном перемещении dl равна:
Работа при перемещении заряда Qo из точки 1 в точку 2:
Рабата не зависит от траектории перемещения, а определяется только положениями начальной 1 и конечной 2 точек. Следовательно, электростатическое поле точечного заряда является потенциальным, а электростатические силы – консервативными.
Работа, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому пути L, равна нулю, т.е.
Этот интеграл называется циркуляцией вектора напряженности. Таким образом, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, обладающее таким свойством, называется потенциальным.
Из обращения в нуль циркуляции вектора Е следует, что линии напряженности электростатического поля не могут быть замкнутыми, они начинаются и кончаются на зарядах (соответственно на положительных или отрицательных) или же уходят в бесконечность.
Теорема о циркуляции вектора напряженности
Теорема о циркуляции вектора напряженности электрического поля
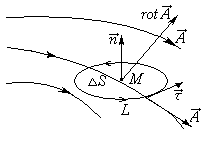
Взаимодействие неподвижных зарядов реализуется посредством электростатического поля. Описывают электростатическое поле при помощи вектора напряженности ($\overline
Электростатические силы являются консервативными, это значит, что их работа по замкнутой траектории ($L$) равна нулю:
В дифференциальной форме теорему о циркуляции записывают как:
\[rot\ \overline
Такой вид записи как (4) удобно использовать для проверки потенциальности векторного поля. Потенциальное поле является безвихревым.
Из теоремы о циркуляции следует, что линии электростатического поля не бывают замкнутыми, они начинаются на положительных, а заканчиваются на отрицательных зарядах.
Теорема о циркуляции вектора напряженности магнитного поля
Физическая величина ($\overline
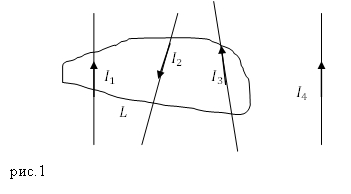
Циркуляция вектора напряженности магнитного поля равна алгебраической сумме токов проводимости, которые охвачены замкнутым контуром, по которому рассматривается циркуляция:
Если направление обхода контура связывается с направлением тока правилом правого винта, то ток в сумме (5) стоит со знаком плюс.
Теорему о циркуляции вектора напряженности магнитного поля доказывают, опираясь на закон Био-Савара-Лапласа и принцип суперпозиции.
Примеры задач с решением
Решение. Из теоремы о циркуляции, которая записана в дифференциальном виде:
\[rot\ \overline
следует, что если вихрь поля равен нулю, то поле потенциально. Используя определение ротора:
Подставляя (1.4) в (1.3), получаем, что
\[rot\ \overline
Ответ. Поле является потенциальным.
Решение. Основой для решения задачи служит теорема о циркуляции вектора напряжённости магнитного поля:
Циркуляция вектора напряженности электростатического поля
Теорема о циркуляции
Электростатическое поле характеризуется циркуляцией его вектора напряженности по замкнутому полю и равняется нулю. Утверждение называют теоремой о циркуляции вектора напряженности электростатического поля.
Следствие теоремы о циркуляции. Теорема Стокса
Так как линии на напряженности электростатического поля незамкнуты, то это применяют в качестве следствия. Их начало идет с положительных зарядов, а заканчивается отрицательными или их уходом в бесконечность. Теорема верна для статичных зарядов.
Еще одним следствием является непрерывность тангенциальных составляющих напряженности. Это говорит о том, что ее компоненты, являющиеся касательными к выбранной любой поверхности во всякой точке, на обеих сторонах содержат одинаковые значения.
Для вычисления ротора применяют формулы:
Представление теоремы о циркуляции в дифференциальном виде:
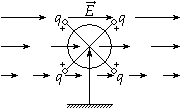
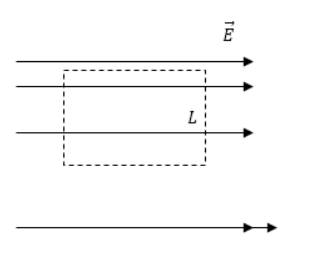
Дан рисунок 3 с изображением электростатического поля. Что можно сказать о его характеристиках?
Решение
По рисунку видно, что существование электростатического поля невозможно. Для выделенного пунктиром контура циркуляции вектора напряженности применяется формула:
Это невозможно, так как существует противоречие теоремы о циркуляции. Определение напряженности поля (измеряется в вольтах на метр В м или в ньютонах на кулон Н К ) идет с помощью густоты силовых линий, причем с различными значениями. Работа по замкнутому кругу не равна нулю, значит, циркуляция вектора напряженности также нулю не равняется.
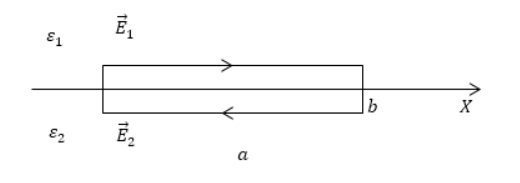
Показать, что тангенциальные составляющие вектора напряженности электростатического поля не изменяются при переходе через границу раздела диэлектриков, основываясь на теореме о циркуляции.
Решение
Выполнение теоремы о циркуляции обусловлено наличием электростатического поля. Его находят из формулы:
Отсюда следует, что
Что такое циркуляция вектора напряженности электростатического поля
| Теорема о циркуляции вектора поля |   |
| Щелкните по ссылке » Потенциал и работа электростатического поля «, чтобы ознакомиться с презентацией раздела в формате PowerPoint. Для возврата к данной странице закройте окно программы PowerPoint. | |||||
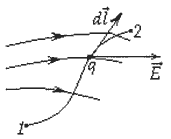
В предыдущей теме было показано, что взаимодействие между покоящимися зарядами осуществляется через электростатическое поле. Описание электростатического поля мы рассматривали с помощью вектора напряженности Существует и другой способ описания поля – с помощью потенциала. Однако для этого необходимо сначала доказать, что силы электростатического поля консервативны, а само поле потенциально. Рассмотрим поле, создаваемое неподвижным точечным зарядом
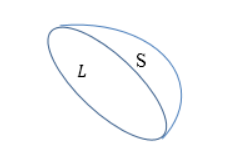
где F(r)– модуль вектора силы Для того, чтобы доказать, что электростатическое поле потенциально, нужно доказать, что силы электростатического поля консервативны. Из раздела «Физические основы механики» известно, что любое стационарное поле центральных сил является консервативным, т.е. работа сил этого поля не зависит от формы пути, а только от положения конечной и начальной точек. Вычислим работу, которую совершает электростатическое поле, созданное зарядом q´ по перемещению заряда q из точки 1 в точку 2. Работа на пути dlравна: где dr – приращение радиус-вектора Тогда полная работа при перемещении q´ из точки 1 в точку 2 равна интегралу: Получили, что работа электростатических сил не зависит от формы пути, а только лишь от координат начальной и конечной точек перемещения. Следовательно, силы поля консервативны, а само поле – потенциально. Этот вывод можно распространить и на поле, созданное системой зарядов, так как по принципу суперпозиции полей: Итак, как и в механике, любое стационарное поле центральных сил является консервативными, т.е. работа сил этого поля не зависит от формы пути, а только от положения начальной и конечной точек. Именно таким свойством обладает электростатическое поле – поле, образованное системой неподвижных зарядов. Если в качестве пробного заряда, перенесенного из точки 1 (рис. 3.2) заданного поля Тогда вся работа равна: Такой интеграл по замкнутому контуру называется циркуляцией вектора Из независимости линейного интеграла от пути между двумя точками следует, что по произвольному замкнутому пути: Это утверждение и называют теоремой о циркуляции Для доказательства теоремы разобьем произвольно замкнутый путь на две части: 1а2 и 2b1 (рис. 3.2). Из сказанного выше следует, что (Интегралы по модулю равны, но знаки противоположны). Тогда работа по замкнутому пути: Поле, обладающее такими свойствами, называется потенциальным. Любое электростатическое поле является потенциальным. Лекция 51.Работа электрического поляИз механики известно определение элементарной работы силы Пусть в электрическом поле существует точечный заряд, который под действием поля перемещается из точки 1 в точку 2.
Считается, что заряд постоянный. Таким образом, работа равна криволинейному интегралу от напряженности, вычисленному вдоль траектории. 2.Работа в поле точечного заряда
Очевидно, что данная работа не зависит от формы траектории, а зависит только от начального и конечного положения заряда. Можно сделать вывод о том, что если заряд перемещается по замкнутой траектории, то работа поля равна нулю. Таким образом, можно записать 3.Теорема о циркуляцииПусть поле создано системой точечных зарядов. Вычислим интеграл от напряженности по замкнутой траектории.
Данное утверждение и составляет суть теоремы о циркуляции. В математике подобный интеграл называют циркуляцией.
| |||||



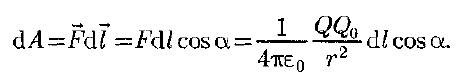
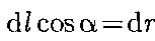
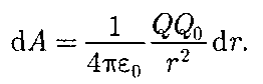
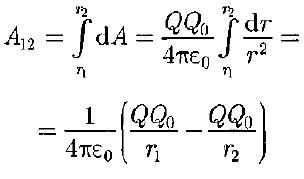
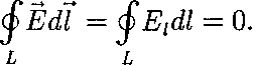

 , равного силе, действующей в данной точке на помещенный в неё пробный единичный положительный заряд
, равного силе, действующей в данной точке на помещенный в неё пробный единичный положительный заряд
 . В любой точке этого поля на пробный точечный заряд q действует сила
. В любой точке этого поля на пробный точечный заряд q действует сила  (рис. 3.1).
(рис. 3.1).
 ,
,  – единичный вектор, определяющий положение заряда q относительно q´, ε0 – электрическая постоянная.
– единичный вектор, определяющий положение заряда q относительно q´, ε0 – электрическая постоянная.
 при перемещении на dl;
при перемещении на dl;  т. е.
т. е.
 .
.


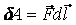
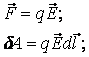
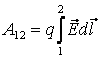
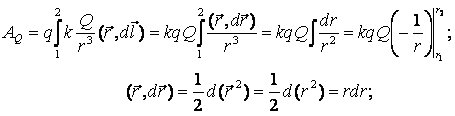
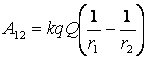
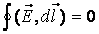

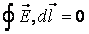

 .
.
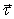 — единичный вектор, касательный к контуру в данной точке, направленный в сторону положительного обхода контура.
— единичный вектор, касательный к контуру в данной точке, направленный в сторону положительного обхода контура.