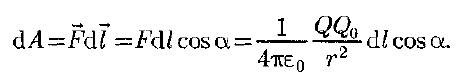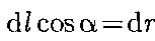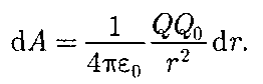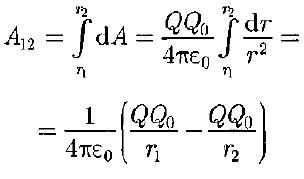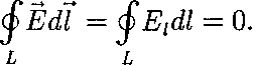Что такое циркуляция вектора напряженности электрического поля

Циркуляция вектора напряженности электростатического поля

Теорема о циркуляции

Электростатическое поле характеризуется циркуляцией его вектора напряженности по замкнутому полю и равняется нулю. Утверждение называют теоремой о циркуляции вектора напряженности электростатического поля.

Следствие теоремы о циркуляции. Теорема Стокса

Так как линии на напряженности электростатического поля незамкнуты, то это применяют в качестве следствия. Их начало идет с положительных зарядов, а заканчивается отрицательными или их уходом в бесконечность. Теорема верна для статичных зарядов.

Еще одним следствием является непрерывность тангенциальных составляющих напряженности. Это говорит о том, что ее компоненты, являющиеся касательными к выбранной любой поверхности во всякой точке, на обеих сторонах содержат одинаковые значения.

Для вычисления ротора применяют формулы:

Представление теоремы о циркуляции в дифференциальном виде:

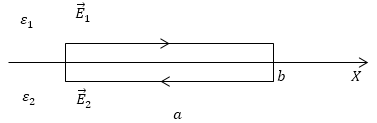
Дан рисунок 3 с изображением электростатического поля. Что можно сказать о его характеристиках?

Решение

По рисунку видно, что существование электростатического поля невозможно. Для выделенного пунктиром контура циркуляции вектора напряженности применяется формула:

Это невозможно, так как существует противоречие теоремы о циркуляции. Определение напряженности поля (измеряется в вольтах на метр В м или в ньютонах на кулон Н К ) идет с помощью густоты силовых линий, причем с различными значениями. Работа по замкнутому кругу не равна нулю, значит, циркуляция вектора напряженности также нулю не равняется.

Показать, что тангенциальные составляющие вектора напряженности электростатического поля не изменяются при переходе через границу раздела диэлектриков, основываясь на теореме о циркуляции.

Решение

Выполнение теоремы о циркуляции обусловлено наличием электростатического поля. Его находят из формулы:

Отсюда следует, что

Источник

Теорема о циркуляции вектора напряженности

Теорема о циркуляции вектора напряженности электрического поля

Взаимодействие неподвижных зарядов реализуется посредством электростатического поля. Описывают электростатическое поле при помощи вектора напряженности ($\overline$), который определен как сила ($\overline$), действующая на единичный положительный заряд, размещенный в рассматриваемой точке поля:

Электростатические силы являются консервативными, это значит, что их работа по замкнутой траектории ($L$) равна нулю:

В дифференциальной форме теорему о циркуляции записывают как:

\[rot\ \overline=0\ \left(4\right).\]

Такой вид записи как (4) удобно использовать для проверки потенциальности векторного поля. Потенциальное поле является безвихревым.

Из теоремы о циркуляции следует, что линии электростатического поля не бывают замкнутыми, они начинаются на положительных, а заканчиваются на отрицательных зарядах.

Теорема о циркуляции вектора напряженности магнитного поля

Физическая величина ($\overline$), являющаяся характеристикой магнитного поля, равная:

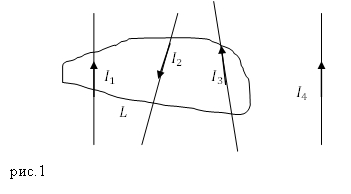
Циркуляция вектора напряженности магнитного поля равна алгебраической сумме токов проводимости, которые охвачены замкнутым контуром, по которому рассматривается циркуляция:

Если направление обхода контура связывается с направлением тока правилом правого винта, то ток в сумме (5) стоит со знаком плюс.

Теорему о циркуляции вектора напряженности магнитного поля доказывают, опираясь на закон Био-Савара-Лапласа и принцип суперпозиции.

Примеры задач с решением

Решение. Из теоремы о циркуляции, которая записана в дифференциальном виде:

\[rot\ \overline=0\ \left(1.1\right).\]

следует, что если вихрь поля равен нулю, то поле потенциально. Используя определение ротора:

Подставляя (1.4) в (1.3), получаем, что

\[rot\ \overline=rot\ \left[A\left(2xy\ \overline+\left(x^2-y^2\right)\overline\right)\right]=0.\]

Ответ. Поле является потенциальным.

Решение. Основой для решения задачи служит теорема о циркуляции вектора напряжённости магнитного поля:

Источник

Циркуляция вектора напряженности электростатического поля

Вы будете перенаправлены на Автор24

Теорема о циркуляции

Ранее мы выяснили, что на заряд (q), который находится в электростатическом поле, действуют консервативные силы, работа ($A$) которых на любом замкнутом пути (L) равна нулю:

Для единичного положительного заряда можем записать:

Интеграл в левой части уравнения (2) есть циркуляция вектора напряженности по контуру L. Характерным свойством электростатического поля является то, что циркуляция его вектора напряжённости по любому замкнутому контуру равна нулю. Такое утверждение называется теоремой о циркуляции вектора напряженности электростатического поля.

Докажем теорему о циркуляции на том основании, что работа поля по перемещению заряда не зависит от траектории перемещения заряда в электростатическом поле, что выражается равенством:

Выражение (4) представим как:

Следствие теоремы о циркуляции

Следствием теоремы о циркуляции является то, что линии напряженности электростатического поля незамкнуты. Они начинаются на положительных зарядах, а заканчиваются на отрицательных или уходят в бесконечность. Теорема верна именно для статичных зарядов. Другое следствие теоремы: непрерывность тангенциальных составляющих напряженности (в отличие от нормальных составляющих). Это значит, что компоненты напряженности, которые являются касательными к выбранной любой поверхности во всякой ее точке, имеют по обе стороны поверхности равные значения.

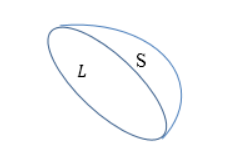
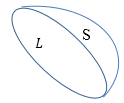
Выделим произвольную поверхность S, которая опирается на контур L (рис.1).

Готовые работы на аналогичную тему

В соответствии с формулой Стокса (теоремой Стокса) интеграл от ротора вектора напряженности ($rot\overrightarrow$), взятый по поверхности S равен циркуляции вектора напряженности вдоль контура, на который опирается данная поверхность:

При практическом вычислении ротора чаще других используют формулы:

Так как в соответствии с уравнением (6) циркуляция вектора напряжённости равна нулю, то мы получаем:

Условие (8) должно выполняться для любой поверхности S, которая опирается на контур L. Это возможно только в том случае, если подынтегральное выражение:

причем для каждой точки поля.

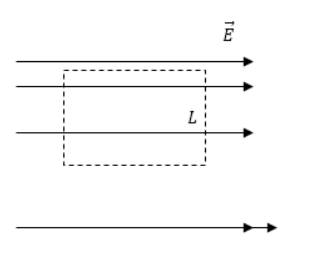
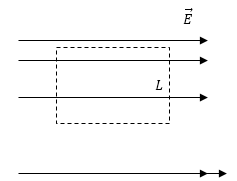
Задание: На рис. 3 изображено электростатическое поле. Что можно сказать о характеристиках данного поля из рисунка?

О данном поле можно сказать, что существование такого электростатического поля невозможно. Если выделить контур (он изображен пунктиром). Для такого контура циркуляция вектора напряженности:

что противоречит теореме о циркуляции для электростатического поля. Напряженность поля определяется густотой силовых линий, она в разных частях поля не одинакова, в результате работа по замкнутому контуру будет отличаться от нуля, следовательно, циркуляция вектора напряженности не равна нулю.

Задание: Исходя из теоремы о циркуляции, покажите, что тангенциальные составляющие вектора напряженности электростатического поля не изменяются при переходе через границу раздела диэлектриков.

Для электростатического поля выполняется теорема о циркуляции, которая выражается уравнением:

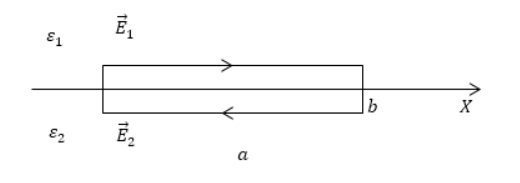
При небольших размерах контура циркуляция вектора напряженности и в соответствии с указанным направлением обхода контура интеграл в формуле (2.1) можно представить как:

\[\oint\limits_L<\overrightarrowd\overrightarrow=E_<1x>a-E_<2x>a+\left\langle E_b\right\rangle 2b=0\ \left(2.2\right),>\]

\[<(E>_<2x>-E_<1x>)a=\left\langle E_b\right\rangle 2b\ (2.3).\]

В таком случае из (2.4) запишем:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 03 12 2021

Источник

Циркуляция вектора напряженности.

Потенциальная энергия заряда.

В потенциальном поле тела обладают потенциальной энергией и работа консервативных сил совершается за счет убыли потенциальной энергии.

Поэтому работу A₁₂ можно представить, как разность потенциальных энергий заряда q₀ в начальной и конечной точках поля заряда q :

Для одноименных зарядов потенциальная энергия их взаимодействия (отталкивания) положительна, для разноименных зарядов потенциальная энергия из взаимодействия (притяжения) отрицательна.

Потенциал электростатического поля.

Отношение не зависит от пробного заряда q0 и является, энергетической характеристикой поля, называемой потенциалом:

Потенциал ϕ в какой-либо точке электростатического поля есть скалярная физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещенного в эту точку.

1.7 Связь между напряженностью и потенциалом.

Связь между потенциалом и напряженностью электростатического поля. Эквипотенциальные поверхности.

Рис.1.13. Эквипотенциа­льные поверхности (сплошные) и силовые линии (пунктирные) поля точечного поло­жительного заряда.

Последнее соотношение представляет связь ос­новных характеристик электро­статического поля Е и j. Здесь — быстрота изменения потенциала в направле­нии силовой линии. Знак ми­нус указывает на то, что вектор направлен в сторону убывания потенциала. Поскольку , можно записать проекции вектора на координатные оси: . Отсюда следует, что . Выраже­ние, стоящее в скобках, называется градиентом скаляра j и обозначается как gradj.

Напряженность электростатического поля равна гра­диенту потенциала, взя­тому с обратным знаком .

1.8 Электроемкость, плоский конденсатор.

Электроемкость.

Электроемкость уединенного проводника численно равна заряду, который нужно сообщить этому проводнику для того, чтобы изменить его потенциал на единицу.

Она зависит от формы и размеров проводника и от диэлектрических свойств окружающей среды. Емкости геометрически подобных проводников пропорциональны их линейным размерам.

Пример: Рассмотрим уединенный шар радиуса R, находящийся в однородной среде с диэлектрической проницаемостью e. Ранее было получено, что потенциал шара ра­вен . Тогда емкость шара , т.е. зависит только от его ра­диуса.

Единица электроемкости —фарад(Ф):1Ф—емкость такогоуединенного проводника, потенциал которого изменяется на 1В при сообщении ему заряда 1Кл. Емкостью 1Ф обладает шар с радиусом R = 9 ⋅10 6 км. Емкость Земли 0,7мФ.

ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между.

ЧТО ПРОИСХОДИТ, КОГДА МЫ ССОРИМСЯ Не понимая различий, существующих между мужчинами и женщинами, очень легко довести дело до ссоры.

Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право.

Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычис­лить, когда этот.

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

Источник

Циркуляция вектора напряженности электростатического поля

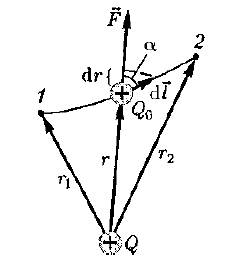
Если в электростатическом поле точечного заряда Q из точки 1 в точку 2 вдоль произвольной траектории перемещается другой точечный заряд Q_o, то сила, приложенная к заряду, совершает работу. Работа силы F на элементарном перемещении dl равна:

Работа при перемещении заряда Q_o из точки 1 в точку 2:

Рабата не зависит от траектории перемещения, а определяется только положениями начальной 1 и конечной 2 точек. Следовательно, электростатическое поле точечного заряда является потенциальным, а электростатические силы – консервативными.

Работа, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому пути L, равна нулю, т.е.

Этот интеграл называется циркуляцией вектора напряженности. Таким образом, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, обладающее таким свойством, называется потенциальным.

Из обращения в нуль циркуляции вектора Е следует, что линии напряженности электростатического поля не могут быть замкнутыми, они начинаются и кончаются на зарядах (соответственно на положительных или отрицательных) или же уходят в бесконечность.

Источник