что такое тригонометрические уравнения

Что такое тригонометрические уравнения

Методы решения тригонометрических уравнений.

1. Алгебраический метод.

( метод замены переменной и подстановки ).

2. Разложение на множители.

преобразуем и разложим на множители выражение в

левой части уравнения:

П р и м е р 2. Решить уравнение: cos 2 x + sin x · cos x = 1.

П р и м е р 3. Решить уравнение: cos 2 x – cos 8 x + cos 6 x = 1.

3. Приведение к однородному уравнению.

а) перенести все его члены в левую часть;

б) вынести все общие множители за скобки;

в) приравнять все множители и скобки нулю;

г ) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на

cos ( или sin ) в старшей степени;

1) tan x = –1, 2) tan x = –3,

4. Переход к половинному углу.

5. Введение вспомогательного угла.

6. Преобразование произведения в сумму.

Источник

Решение тригонометрических уравнений — 39 примеров!

Привет, самый лучший ученик во Вселенной!

Сегодня мы с тобой изучим, как решать одну из разновидностей уравнений – тригонометрические. Мы решим 39(!) примеров, от самых простых, до самых сложных.

И станем на шаг ближе к заветной цели – сдать ЕГЭ по математике так, чтобы поступить в ВУЗ мечты!

Тригонометрические уравнения — коротко о главном

Тригонометрическое уравнение – это уравнение, в котором неизвестная находится строго под знаком тригонометрической функции.

Существует два способа решения тригонометрических уравнений:

Первый способ – с использованием формул.

Второй способ – через тригонометрическую окружность.

Тригонометрическая окружность позволяет измерять углы, находить их синусы, косинусы и прочее.

Чтобы уметь решать тригонометрические уравнения необходимо знать как минимум следующее:

Если ты что-то не знаешь, повтори следующие разделы:

Этого будет вполне достаточно. Если это по ходу моего повествования окажется не так, то не сердись, придётся вспомнить что-нибудь ещё, не упомянутое здесь.

Простейшие тригонометрические уравнения

Что же это такое, как ты думаешь? Является ли, например, уравнение

Ты и сам прекрасно понимаешь, что нет! Потому что ни одной тригонометрической функции \( \displaystyle \left( sin x,cos x,tg x,ctg x \right)\) в нём и в помине нет!

А что насчёт вот такого уравнения?

И опять ответ отрицательный!

Это так называемое уравнение смешанного типа.

Оно содержит как тригонометрическую составляющую, так и линейную (\( \displaystyle 3x\)).

Некоторые типы подобных уравнений мы будем с тобой решать в следующих раздела этой статьи.

Но вернёмся к вопросу: «Что же такое тригонометрические уравнения?»

Тригонометрические уравнения –это уравнения, в которых неизвестная находится строго под знаком тригонометрической функции!

Однако для начала мы не будем решать сложные и иногда неприступные тригонометрические уравнения, а ограничимся самыми простыми уравнениями вида:

Где \( \displaystyle a\) – некоторое постоянное число.

Например: \( \displaystyle 0,5;

\( \displaystyle f\left( x \right)\) – некоторая функция, зависящая от искомой переменной \( \displaystyle x\), например \( \displaystyle f\left( x \right)=x,

f\left( x \right)=\frac<\pi x><7>\) и т. д.

Такие уравнения называются простейшими!

Основная цель решения ЛЮБОГО тригонометрического уравнения – это свести его к виду простейшего!

Для этого, как правило, используют аппарат, который я описал в разделе «Формулы тригонометрии«

Так что очень важно, я бы даже сказал, жизненно необходимо научиться решать простейшие уравнения, ибо они – фундамент для решения сложных примеров.

Как часто тригонометрические уравнения встречаются на ЕГЭ?

Тригонометрические уравнения могут встретиться до четырех раз в заданиях ЕГЭ. Это может быть:

Так что, как ты понимаешь, при некоторых раскладах, навык решения данного вида уравнений может добавить в твою копилку аж 5 первичных баллов из 32!

Два способа решения тригонометрических уравнений – через формулы и по кругу

В принципе, я не могу сказать, что легче: держать в голове, как строится круг, или помнить 4 формулы.

Тут решать тебе самому, однако я всё же предпочитаю решать данные уравнения через формулы, поэтому здесь я буду описывать именно этот метод.

Вначале мы начнём с «самых простейших» из простейших уравнений вида:

Я хочу сразу оговориться вот о чем, будь внимателен:

То есть, тебе не надо знать вообще никаких формул, чтобы спокойно ответить, что уравнения, например:

\( \displaystyle cos\left( 3-sin\left( x \right) \right)=2\)

\( \displaystyle sin\left( 2<^<2>>-2x+1 \right)=-3\)

Корней не имеют.

Потому что они «не попадают» в промежуток от минус единицы до плюс единицы.

Ещё раз скажу: внимательно обдумай эти слова, они уберегут тебя от многих глупых ошибок.

Для остальных же случаев тригонометрические формулы такие как в этой таблице.

На самом деле в этой таблице данных немного больше, чем нужно.

Тебе нужно лишь запомнить первые два её столбца, другие столбцы – частные случаи решения тригонометрических уравнений.

Я, допустим, никогда не утруждаю себя их запоминанием, а вывожу ответ из основных формул.

Глядя на таблицу, не возникло ли у тебя пары вопросов?

У меня бы возникли вот какие:

Что такое \( \displaystyle n\) и что такое, например \( \displaystyle arcsin\alpha

Отвечаю на все по порядку:

В чем уникальная особенность тригонометрических уравнений перед всеми остальными, которые ты изучал?

ОНИ ИМЕЮТ БЕСКОНЕЧНОЕ КОЛИЧЕСТВО КОРНЕЙ.

И число \( \displaystyle n\) и служит для обозначения этой «бесконечности».

Конечно, вместо \( \displaystyle n\) можно писать любую другую букву, только не забывай добавить в ответе: \( \displaystyle n\in Z\) – что означает, что \( \displaystyle n\) – есть любое целое число.

Теперь насчёт арксинуса и других «арок». Вообще, так записываются обратные тригонометрические функции и понимать, скажем, \( \displaystyle arcsin\alpha \) надо как «угол, синус которого равен \( \displaystyle \alpha \)«

Алгоритм вычисления арксинусов и других «арок»

Вот простой пример вычисления аркосинуса:

\( \displaystyle \arccos \left( \frac<\sqrt<3>> <2>\right)\)

\( \displaystyle \frac<\pi ><6>\) и \( \displaystyle \frac<\pi ><3>\).

Если «арка» берется от отрицательного числа?

Всё ли я сказал про «арки»? Почти что да! Остался вот какой момент.

Что делать, если «арка» берётся от отрицательного числа?

Лезть в таблицу – как бы не так! Для арок выполняются следующие формулы:

И внимание.

Чтобы запомнить, ориентируемся на обычные тригонометрические функции: грубо говоря, синус и тангенс мы смотрим на тригонометрической окружности по вертикальной оси, а косинус и котангенс – по горизонтальной.

Соответственно, для арксинуса и арктангенса выбираем две четверти по вертикали: первую и четвёртую (минусик выносится из аргумента и ставится перед функцией), а для арккосинуса и арккотангенса – по горизонтали: первую и вторую.

В первой и второй четвертях аргумент уже не может быть отрицательным, поэтому и получаются формулы не совсем похожими.

Ну всё, теперь мы можем приступать к решению простейших уравнений!

Решение 11-ти простейших тригонометрических уравнений

Уравнение 1. \( \displaystyle sin\left( x \right)=0,5\)

Запишу по определению:

Всё готово, осталось только упростить, посчитав значение арксинуса.

Источник

Понятие о тригонометрическом уравнении. Простейшие тригонометрические уравнения.

Содержание

Понятие о тригонометрическом уравнении.

Уравнение называется тригонометрическим, если в нём содержится любая тригонометрическая функция.

В силу того, что тригонометрическая функция периодична, тригонометрические уравнения имеют множество решений или не имеют их вообще.

Существуют 2 основных способа решения тригонометрических уравнений:

Простейшие тригонометрические уравнения.

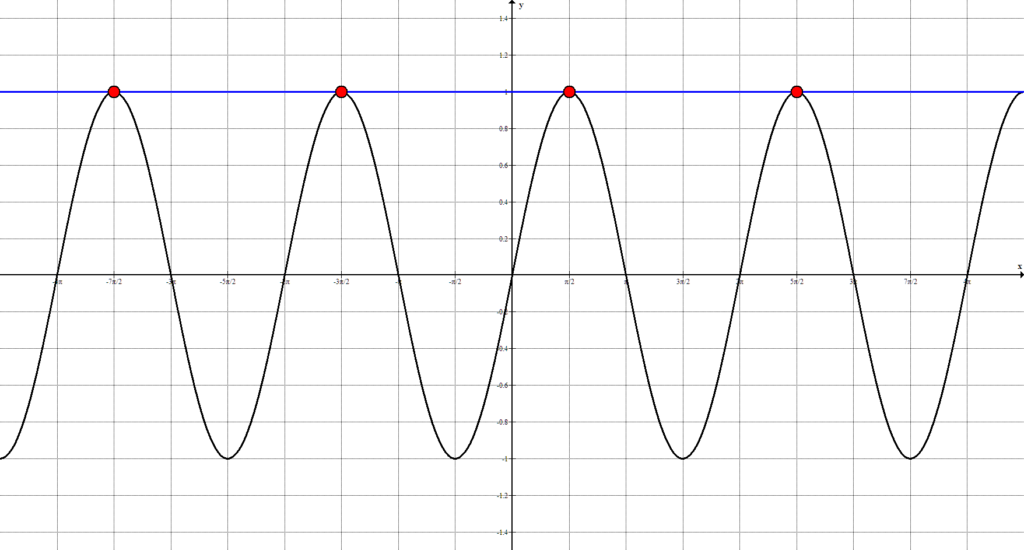
Решим несколько простейших тригонометрических уравнений.

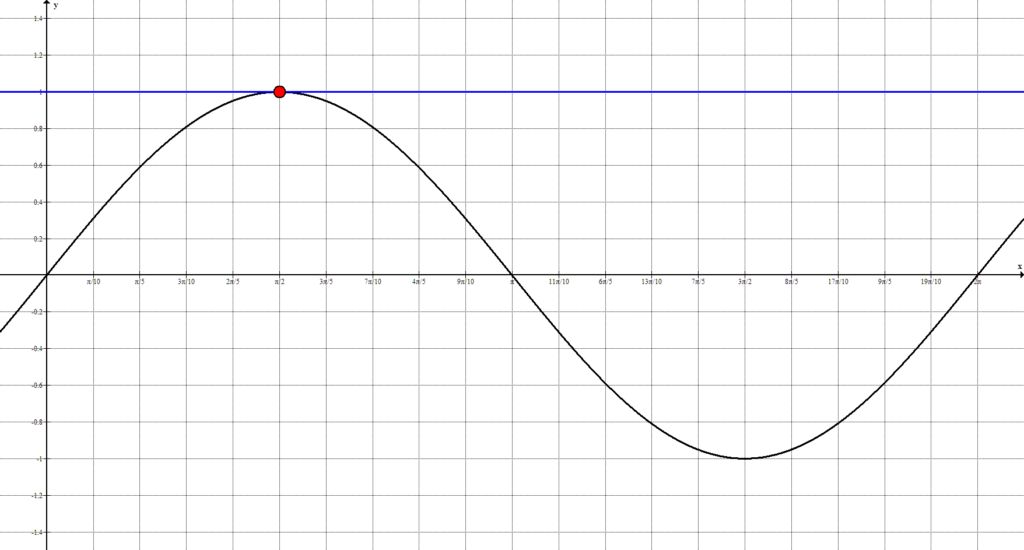
Видим, что количество точек пересечения достаточно велико, а, значит, необходимо выявить закономерность. Так как тригонометрические функции являются периодическими, то все точки, попавшие на 1-ый положительный период, будут периодически повторятся. Рассмотрим решения, попавшие на 1-ый период:

$x = \frac<\pi> <2>+ 2\pi n, \ n \in \mathbb$.

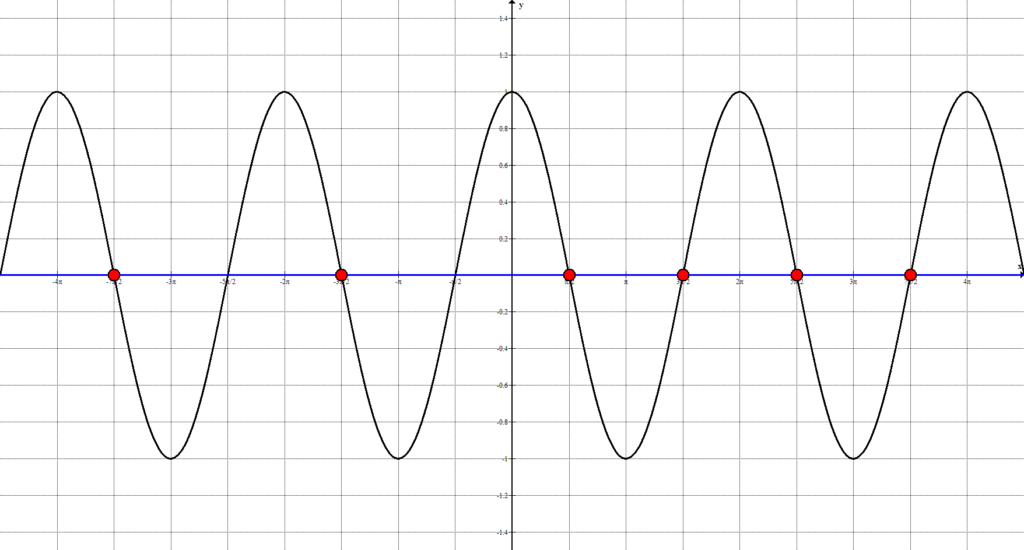
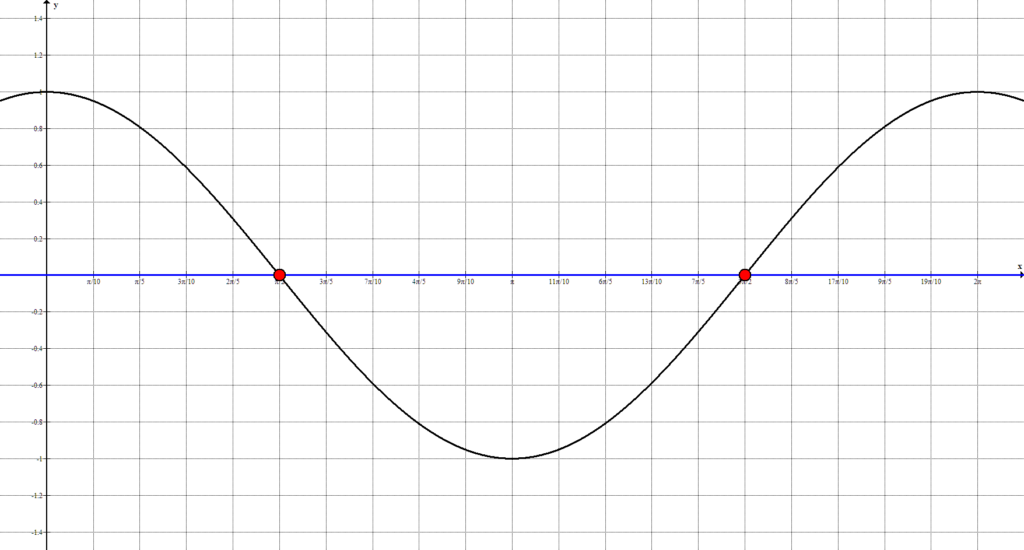
Видим, что количество точек пересечения достаточно велико, а, значит, необходимо выявить закономерность. Так как тригонометрические функции являются периодическими, то все точки, попавшие на 1-ый положительный период, будут периодически повторятся. Рассмотрим решения, попавшие на 1-ый период:

Получены два решения:

которые можно попытаться объединить в одно.

Не все решения можно объединить в одно. Если это невозможно, то в ответ выписываются 2 решения.

$x = \frac<\pi> <2>+ \pi n, \ n \in \mathbb$

Таблица решений простейших тригонометрических уравнений.

Ограничения тригонометрических уравнений.

Источник

Простейшие тригонометрические уравнения. Часть 1

Простейшими называются тригонометрические уравнения следующих четырёх видов:

Любое тригонометрическое уравнение в конечном счёте сводится к решению одного или нескольких простейших. К сожалению, на этом заключительном стандартном шаге школьники часто допускают ошибки, что ведет к потере баллов на ЕГЭ. Именно поэтому так важна данная тема.

Существуют два подхода к решению простейших тригонометрических уравнений.
Первый подход — бессмысленный и тяжёлый. Следуя ему, надо выучить по шпаргалке общие формулы, а также все частные случаи. Польза от этого столь же невелика, как от зубрежки шестнадцати строк заклинаний на непонятном языке. Мы отказываемся от такого подхода раз и навсегда.

Второй подход — логический и наглядный. Для решения простейших тригонометрических уравнений мы пользуемся тригонометрическим кругом и определениями тригонометрических функций.

Уравнения и

Абитуриент, будь внимателен! Уравнения или решений не имеют!

Начнём с самых простых уравнений.

Следовательно, все эти углы могут быть записаны одной формулой:

Это и есть множество решений данного уравнения. Напоминаем, что — это множество целых чисел.

Снова видим, что на единичной окружности есть лишь одна точка с абсциссой :

Эта точка соответствует углу и всем углам, отличающихся от на несколько полных оборотов в обе стороны, т. е. на целое число полных углов. Следовательно, все решения данного уравнения записываются формулой:

И записываем ответ:

Обсуждать тут уже нечего, не так ли? 🙂

Можете, кстати, записать ответ и в другом виде:

На тригонометрическом круге имеются две точки с ординатой 0:

Эти точки соответствуют углам Все эти углы получаются из нулевого угла прибавлением целого числа углов (т. е. с помощью нескольких полуоборотов в обе стороны). Таким образом,

Точки, лежащие на концах диаметра тригонометрического круга, мы будем называть диаметральной парой.

Точки с абсциссой 0 также образуют диаметральную пару, на сей раз вертикальную:

Все углы, отвечающие этим точкам, получаются из — прибавлением целого числа углов (полуоборотов):

Теперь мы можем сделать и второе полезное наблюдение.

Переходим к следующему этапу. Теперь в правой части будет стоять табличное значение синуса или косинуса (отличное от 0 или ). Начинаем с косинуса.

Имеем вертикальную пару точек с абсциссой :

Все углы, соответствующие верхней точке, описываются формулой (вспомните первое полезное наблюдение!):

Аналогично, все углы, соответствующие нижней точке, описываются формулой:

Обе серии решений можно описать одной формулой:

Остальные уравнения с косинусом решаются совершенно аналогично. Мы приводим лишь рисунок и ответ.

Теперь рассмотрим уравнения с синусом. Тут ситуация немного сложнее.

Имеем горизонтальную пару точек с ординатой :

Углы, отвечающие правой точке:

Углы, отвечающие левой точке:

Описывать эти две серии одной формулой никто не заставляет. Можно записать ответ в таком виде:

Тем не менее, объединяющая формула существует, и её надо знать. Выглядит она так:

Остальные уравнения с синусом решаются точно так же. Мы приводим рисунок, запись ответа в виде совокупности двух серий и объединяющую формулу.

На этом с синусом и косинусом пока всё. Переходим к тангенсу.

Линия тангенсов.

Начнём с геометрической интерпретации тангенса — так называемой линии тангенсов. Это касательная к единичной окружности, параллельная оси ординат (см. рисунок).

Из подобия треугольников и имеем:

Мы рассмотрели случай, когда находится в первой четверти. Аналогично рассматриваются случаи, когда находится в остальных четвертях. В результате мы приходим к следующей геометрической интерпретации тангенса.

Вот рисунок в случае, когда находится во второй четверти. Тангенс угла отрицателен.

Уравнение

.
Имеем диаметральную горизонтальную пару точек:

Эта пара, как мы уже знаем, описывается формулой:

Имеем диаметральную пару:

Вспоминаем второе полезное наблюдение и пишем ответ:

Остальные уравнения с тангенсом решаются аналогично. Мы приводим лишь рисунки и ответы.

На этом заканчиваем пока и с тангенсом.

Уравнение нет смысла рассматривать особо. Дело в том, что:
уравнение равносильно уравнению ;

Итак, мы разобрали простейшие тригонометрические уравнения, содержащие в правой части табличные значения тригонометрических функций. Именно такие задачи встречаются в части В вариантов ЕГЭ.

Источник

Основные виды тригонометрических уравнений (задание 13)

Рассмотрим некоторые наиболее часто встречающиеся виды тригонометрических уравнений и способы их решения.

Пример 1. Решить уравнение \(6\cos^2x-13\sin x-13=0\)

Пример 2. Решить уравнение \(5\sin 2x=\cos 4x-3\)

Пример 3. Решить уравнение \(\mathrm\, x+3\mathrm\,x+4=0\)

Сделаем обратную замену:

Пример 4. Решить уравнение \(11\cos 2x-3=3\sin 3x-11\sin x\)

При помощи формул \(\sin 3x=3\sin x-4\sin^3x\) и \(\cos2x=1-2\sin^2x\) можно свести уравнение к уравнению только с \(\sin x\) :

Таким образом, корень \(t_3\) не подходит. Сделаем обратную замену:

\(\blacktriangleright\) Однородные тригонометрические уравнения второй степени: \[I. \quad <\Large>, \quad a\ne 0,c\ne 0\]

Аналогично и \(\sin x=0\) не является решением такого уравнения.

Таким образом, данное уравнение при помощи деления на \(\cos^2x\) и замены \(t=\mathrm\,x\) сводится к квадратному уравнению:

Уравнения вида \[I’. \quad <\Large>, \quad a\ne0,c\ne 0\] с легкостью сводятся к уравнению вида \(I\) с помощью использования основного тригонометрического тождества: \[d=d\cdot 1=d\cdot (\sin^2x+\cos^2x)\]

Заметим, что благодаря формуле \(\sin2x=2\sin x\cos x\) однородное уравнение можно записать в виде

\(a\sin^2 x+b\sin 2x+c\cos^2x=0\)

Пример 5. Решить уравнение \(2\sin^2x+3\sin x\cos x=3\cos^2x+1\)

Подставим вместо \(1=\sin^2x+\cos^2x\) и получим:

\(\blacktriangleright\) Однородные тригонометрические уравнения первой степени: \[II.\quad <\Large>, a\ne0, b\ne 0\]

Аналогично и \(\sin x=0\) не является решением такого уравнения.

Пример 6. Решить уравнение \(\sin x+\cos x=0\)

Разделим правую и левую части уравнения на \(\sin x\) :

\(1+\mathrm\, x=0 \Rightarrow \mathrm\, x=-1 \Rightarrow x=-\dfrac<\pi>4+\pi n, n\in\mathbb\)

\(\blacktriangleright\) Неоднородные тригонометрические уравнения первой степени: \[II.\quad <\Large>, a\ne0, b\ne 0, c\ne 0\]

Существует несколько способов решения подобных уравнений. Рассмотрим те из них, которые можно использовать для любого такого уравнения:

1 СПОСОБ: при помощи формул двойного угла для синуса и косинуса и основного тригонометрического тождества: \(<\large<\sin x=2\sin<\dfrac x2>\cos<\dfrac x2>, \qquad \cos x=\cos^2 <\dfrac x2>-\sin^2 <\dfrac x2>,\qquad c=c\cdot \Big(\sin^2 <\dfrac x2>+\cos^2 <\dfrac x2>\Big)>>\) данное уравнение сведется к уравнению \(I\) :

Пример 7. Решить уравнение \(\sin 2x-\sqrt3 \cos 2x=-1\)

2 СПОСОБ: при помощи формул выражения функций через тангенс половинного угла: \[\begin <|lc|cr|>\hline &&&\\ \sin<\alpha>=\dfrac<2\mathrm\, \dfrac<\alpha>2><1+\mathrm^2\, \dfrac<\alpha>2> &&& \cos<\alpha>=\dfrac<1-\mathrm^2\, \dfrac<\alpha>2><1+\mathrm^2\, \dfrac<\alpha>2>\\&&&\\ \hline \end\] уравнение сведется к квадратному уравнению относительно \(\mathrm\, \dfrac x2\)

Пример 8. Решить то же уравнение \(\sin 2x-\sqrt3 \cos 2x=-1\)

Таким образом, мы получили то же уравнение, что и, решая первым способом.

3 СПОСОБ: при помощи формулы вспомогательного угла.
\[<\large\,\sin (x+\phi),>> \quad \text <где >\cos \phi=\dfrac a<\sqrt>\]

Для использования данной формулы нам понадобятся формулы сложения углов: \[\begin <|lc|cr|>\hline &&&\\ \sin<(\alpha\pm \beta)>=\sin\alpha\cdot \cos\beta\pm \sin\beta\cdot \cos\alpha &&& \cos<(\alpha\pm \beta)>=\cos\alpha\cdot \cos\beta \mp \sin\alpha\cdot \sin\beta\\ &&&\\ \hline \end\]

Пример 9. Решить то же уравнение \(\sin 2x-\sqrt3 \cos 2x=-1\)

Т.к. мы решаем уравнение, то можно не преобразовывать левую часть, а просто разделить обе части уравнения на \(\sqrt<1^2+(-\sqrt3)^2>=2\) :

\(\dfrac12\sin 2x-\dfrac<\sqrt3>2\cos 2x=-\dfrac12\)

\(\sin 2x\cos \dfrac<\pi>3-\sin \dfrac<\pi>3\cos 2x=-\dfrac12 \Rightarrow \sin\left(2x-\dfrac<\pi>3\right)=-\dfrac12\)

Решениями данного уравнения являются:

Заметим, что при решении уравнения третьим способом мы добились “более красивого” ответа (хотя ответы, естественно, одинаковы), чем при решении первым или вторым способом (которые, по сути, приводят уравнение к одному и тому же виду).
Таким образом, не стоит пренебрегать третьим способом решения данного уравнения.

\(\blacktriangleright\) Если тригонометрическое уравнение можно свести к виду \[<\Large>, \text <где >a\ne 0, b\ne 0,\] то с помощью формулы \[<\large<(\sin x\pm\cos x)^2=1\pm2\sin x\cos x>> \ \ (*)\] данное уравнение можно свести к квадратному.

\(\blacktriangleright\) Формулы сокращенного умножения в тригонометрическом варианте:

\(I\) Квадрат суммы или разности \((A\pm B)^2=A^2\pm 2AB+B^2\) :

\((\sin x\pm \cos x)^2=\sin^2 x\pm 2\sin x\cos x+\cos^2x=(\sin^2 x+\cos^2 x)\pm 2\sin x\cos x=1\pm \sin 2x\)

\(II\) Разность квадратов \(A^2-B^2=(A-B)(A+B)\) :

\((\cos x-\sin x)(\cos x+\sin x)=\cos^2x-\sin^2x=\cos 2x\)

\(III\) Сумма или разность кубов \(A^3\pm B^3=(A\pm B)(A^2\mp AB+B^2)\) :

\(\sin^3x\pm \cos^3x=(\sin x\pm \cos x)(\sin^2x\mp \sin x\cos x+\cos^2x)=(\sin x\pm \cos x)(1\mp \sin x\cos x)=\)

\(=(\sin x\pm \cos x)(1\mp \frac12\sin 2x)\)

\(IV\) Куб суммы или разности \((A\pm B)^3=A^3\pm B^3\pm 3AB(A\pm B)\) :

\((\sin x\pm \cos x)^3=(\sin x\pm \cos x)(\sin x\pm \cos x)^2=(\sin x\pm \cos x)(1\pm \sin 2x)\) (по первой формуле)

Источник