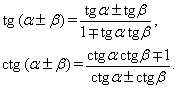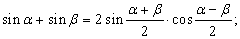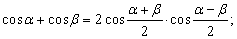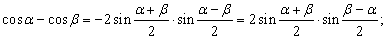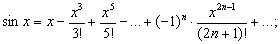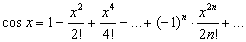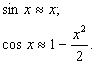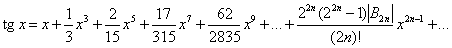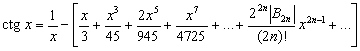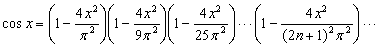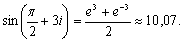что такое тригонометрическая функция определение
Тригонометрия: определение тригонометрических функций
Впервые с определением синуса, косинуса, тангенса и котангенса школьники встречаются в восьмом классе в курсе геометрии. Напомню эти определения. Рассмотрим прямоугольный треугольник: 
sin A=a/b; sin C=c/b
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе:
cos A=c/b; cos C= a/b
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему:
tg A=a/c; tg C=c/a.
Эти определения тригонометрических функций удобно использовать при решении геометрических задач, связанных с нахождением сторон и углов в прямоугольном треугольнике, однако они не улучшают понимания того, что из себя представляют тригонометрические функции именно как функции.
Часто во время занятий со школьниками я сталкиваюсь с тем, что они не понимают, откуда «взялись» тригонометрические функции, что они из себя представляют, и как их «готовить», чтобы легко решать уравнения и неравенства, содержащие тригонометрические функции.
Предлагаю вам посмотреть ВИДЕОУРОК, чтобы понять, что такое синус, косинус, тангенс и котангенс, как они между собой связаны, и как легко определять знаки тригонометрических функций без использования таблиц.
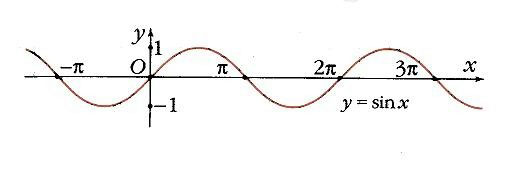
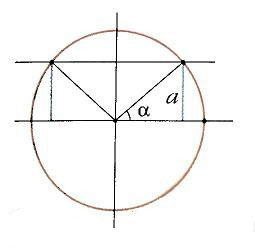
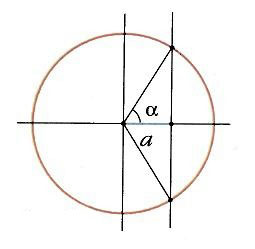
Косинусом угла α называется абсцисса (то есть координата по оси OX) точки на единичной окружности, соответствующей данному углу α.
Синусом угла α называется ордината (то есть координата по оси OY ) точки на единичной окружности, соответствующеий данному углу α.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса (x), синус — ордината (y).
Поскольку радиус окружности равен 1, для любого угла и синус, и косинус находятся в пределах от −1 до 1:
−1 ≤ cos α ≤ 1, −1 ≤ sin α ≤ 1.
Основное тригонометрическое тождество является следствием теоремы Пифагора (квадрат гипотенузы равен сумме квадратов катетов):
sin 2 α+ cos 2 α = 1
Чтобы узнать знаки синуса и косинуса какого-либо угла, находим на нашей окружности точку, соответствующую данному углу α, смотрим, положительны или отрицательны её координаты по x (это косинус угла α) и по y (это синус угла α).
Купить видеокурс «ВСЯ ТРИГОНОМЕТРИЯ. Часть В и 13»
История тригонометрических функций
Самой первой тригонометрической функцией была хорда, соответствующая данной дуге. Для этой функции были построены первые тригонометрические таблицы (II в. до н. э.), нужные для астрономии.
Впервые в истории науки в период V-XII веков индийские математики и астрономы вместо полной хорды стали рассматривать половину хорды, которая соответствует современному понятию синуса. Величину половины хорды они назвали “архиджива”, что означало “половина тетивы лука”. Кроме sin x, индийцы рассматривали также величину 1 – cos x, которую они называли “комаджива”, и величину cos x – “котиджива”.
Понятие таких тригонометрических функций, как тангенс, котангенс, секанс и косеканс, определил совершенно строго, исходя из рассмотрения тригонометрического круга, иранский математик Абу-ль-Вефа. Современные названия этих функций были даны в период с XV по XVII век европейскими учеными. Так, термин “тангенс” с латинского “касательная” был введен в XV веке основателем тригонометрии в Европе Региомонтаном. В XVI веке Финк вводит термин “секанс”. В XVII веке помощник изобретателя десятичных логарифмов Бриггса ученый Гюнтер вводит название “косинус” и “котангенс”, причем приставка “ко” (co) обозначает дополнение (complementum).
Современные обозначения синуса и косинуса знаками sin x и cos x были впервые введены в 1739 году И. Бернулли в письме к петербургскому математику Л. Эйлеру. Последний пришел к выводу, что эти обозначения весьма удобны, и стал употреблять их в своих математических работах. Кроме того, Эйлер вводит следующие сокращенные обозначения тригонометрических функций угла x: tang x, cot x, sec x, cosec x. Далее Эйлер установил связь тригонометрических функций с показательными и дал правило для определения знаков функций в различных четвертях круга. Эйлер установил современную точку зрения на тригонометрические как функции числового аргумента.
В1770 г. появилось и удерживается до наших дней название Тригонометрические функции. Его ввел Г. С. Клюгель в работе “Аналитическая тригонометрия”.
Определение и графики тригонометрических функций
Величины углов (аргументы функций): α, x
Тригонометрические функции: sinα, cosα, tanα, cotα, secα, cscα
Множество действительных чисел: R
Координаты точки окружности: x, y
Радиус круга: r
Целые числа: k
1. Тригонометрические функции представляют собой элементарные функции, аргументом которых является угол. С помощью тригонометрических функций описываются соотношения между сторонами и острыми углами в прямоугольном треугольнике. Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье). Данные функции часто появляются при решении дифференциальных и функциональных уравнений.
2. К тригонометрическим функциям относятся следующие 6 функций: синус, косинус, тангенс,котангенс, секанс и косеканс. Для каждой из указанных функций существует обратная тригонометрическая функция.
3. Геометрическое определение тригонометрических функций удобно ввести с помощью единичного круга. На приведенном ниже рисунке изображен круг радиусом r=1. На окружности обозначена точка M(x,y). Угол между радиус-вектором OM и положительным направлением оси Ox равен α.
4. Синусом угла α называется отношение ординаты y точки M(x,y) к радиусу r:
sinα=y/r.
Поскольку r=1, то синус равен ординате точки M(x,y).
5. Косинусом угла α называется отношение абсциссы x точки M(x,y) к радиусу r:
cosα=x/r
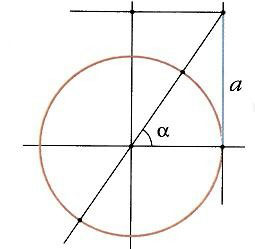
6. Тангенсом угла α называется отношение ординаты y точки M(x,y) к ee абсциссе x:
tanα=y/x,x≠0
7. Котангенсом угла α называется отношение абсциссы x точки M(x,y) к ее ординате y:
cotα=x/y,y≠0
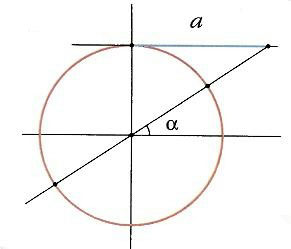
8. Секанс угла α − это отношение радиуса r к абсциссе x точки M(x,y):
secα=r/x=1/x,x≠0
9. Косеканс угла α − это отношение радиуса r к ординате y точки M(x,y):
cscα=r/y=1/y,y≠0
10. В единичном круге проекции x, y точки M(x,y) и радиус r образуют прямоугольный треугольник, в котором x,y являются катетами, а r − гипотенузой. Поэтому, приведенные выше определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом:
Синусом угла α называется отношение противолежащего катета к гипотенузе.
Косинусом угла α называется отношение прилежащего катета к гипотенузе.
Тангенсом угла α называется противолежащего катета к прилежащему.
Котангенсом угла α называется прилежащего катета к противолежащему.
Секанс угла α представляет собой отношение гипотенузы к прилежащему катету.
Косеканс угла α представляет собой отношение гипотенузы к противолежащему катету.
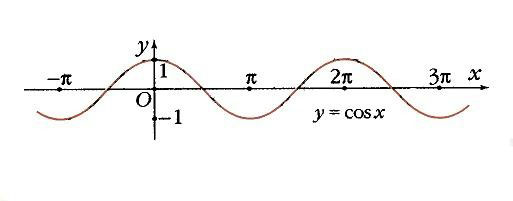
11. График функции синус
y=sinx, область определения: x∈R, область значений: −1≤sinx≤1
12. График функции косинус
y=cosx, область определения: x∈R, область значений: −1≤cosx≤1
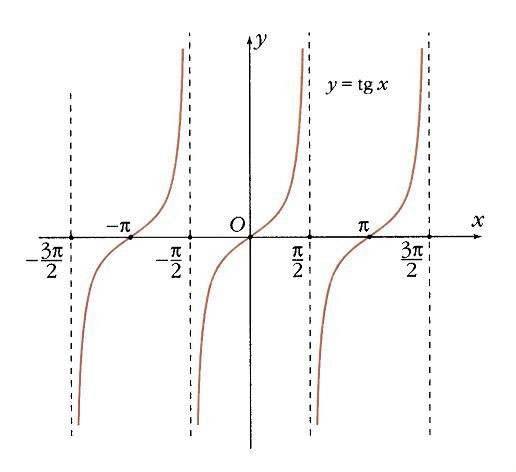
13. График функции тангенс
y=tanx, область определения: x∈R,x≠(2k+1)π/2, область значений: −∞ Где применяется тригонометрия
Тригонометрические вычисления применяются практически во всех сферах жизнедеятельности людей. Следует отметить применение в таких областях как: астрономия, физика, природа, биология, музыка, медицина и многие другие.
Тригонометрия в астрономии:
Потребность в решении треугольников раньше всего обнаружилась в астрономии; поэтому, в течение долгого времени тригонометрия развивалась и изучалась как один из разделов астрономии.
Потребность в решении треугольников раньше всего обнаружилась в астрономии; поэтому, в течение долгого времени тригонометрия развивалась и изучалась как один из разделов астрономии.
Составленные Гиппархом таблицы положений Солнца и Луны позволили предвычислять моменты наступления затмений (с ошибкой 1—2 ч). Гиппарх впервые стал использовать в астрономии методы сферической тригонометрии. Он повысил точность наблюдений, применив для наведения на светило крест нитей в угломерных инструментах — секстантах и квадрантах. Ученый составил огромный по тем временам каталог положений 850 звезд, разделив их по блеску на 6 степеней (звездных величин). Гиппарх ввел географические координаты — широту и долготу, и его можно считать основателем математической географии. (ок. 190 до н. э. — ок. 120 до н. э.)
Достижения Виета в тригонометрии
Полное решение задачи об определении всех элементов плоского или сферического треугольников по трем данным элементам, важные разложения sin пх и cos пх по степеням cos х и sinx. Знание формулы синусов и косинусов кратных дуг дало возможность Виету решить уравнение 45-й степени, предложенное математиком А. Рооменом; Виет показал, что решение этого уравнения сводится к разделению угла на 45 равных частей и что существуют 23 положительных корня этого уравнения. Виет решил задачу Аполлония с помощью линейки и циркуля.
Решение сферических треугольников- одна из задач астрономии Вычислять стороны и углы любого сферического треугольника по трем подходящим образом заданным сторонам или углам позволяют следующие теоремы: (теорема синусов) (теорема косинусов для углов) (теорема косинусов для сторон).
Тригонометрия в физике:
В окружающем нас мире приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Эти процессы называются колебательными. Колебательные явления различной физической природы подчиняются общим закономерностям и описываются одинаковыми уравнениями. Существуют разные виды колебательных явлений.
Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом:
Где х — значение изменяющейся величины, t — время, А — амплитуда колебаний, ω — циклическая частота колебаний, — полная фаза колебаний, r — начальная фаза колебаний.
Обобщенное гармоническое колебание в дифференциальном виде x’’ + ω²x = 0.
Тригонометрия в природе.
Впервые теория радуги была дана в 1637 году Рене Декартом. Он объяснил радугу, как явление, связанное с отражением и преломлением света в дождевых каплях.
Северное сияние Проникновение в верхние слои атмосферы планет заряженных частиц солнечного ветра определяется взаимодействием магнитного поля планеты с солнечным ветром.
Сила, действующая на движущуюся в магнитном поле заряженную частицу называется силой Лоренца. Она пропорциональна заряду частицы и векторному произведению поля и скорости движения частицы.
· Американские ученые утверждают, что мозг оценивает расстояние до объектов, измеряя угол между плоскостью земли и плоскостью зрения.
· К тому же в биологии используется такое понятие как синус сонный, синус каротидный и венозный или пещеристый синус.
Тригонометрия и тригонометрические функции в медицине и биологии.
· Биологические ритмы, биоритмы – это более или менее регулярные изменения характера и интенсивности биологических процессов.
· Основной земной ритм – суточный.
· Модель биоритмов можно построить с помощью тригонометрических функций.
Тригонометрия в биологии
Какие биологические процессы связаны с тригонометрией?
· Биологические ритмы, биоритмы связаны с тригонометрией
Связь биоритмов с тригонометрией
· Модель биоритмов можно построить с помощью графиков тригонометрических функций. Для этого необходимо ввести дату рождения человека ( день, месяц, год ) и длительность прогноза
Движение рыб в воде происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения.
При полёте птицы траектория взмаха крыльев образует синусоиду.
Возникновение музыкальной гармонии
· Согласно дошедшим из древности преданиям, первыми, кто попытался сделать это, были Пифагор и его ученики.
· Частоты, соответствующие одной и той же ноте в первой, второй и т.д. октавах, относятся, как 1:2:4:8…
· диатоническая гамма 2:3:5
Тригонометрия в архитектуре
· Детская школа Гауди в Барселоне
· Страховая корпорация Swiss Re в Лондоне
· Феликс Кандела Ресторан в Лос-Манантиалесе
Значения тригонометрических функций
Ключевые слова: радиан, радианная мера угла, тригонометрическая окружность, знаки тригонометрических функций
Значит, можно написать следующие формулы перехода от градусного измерения к радианному:
=180рад
Пользуясь этими формулами, легко получить следующую таблицу перевода некоторых наиболее часто встречающихся углов из градусной меры в радианную и обратно.
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ – один из классов элементарных функций.
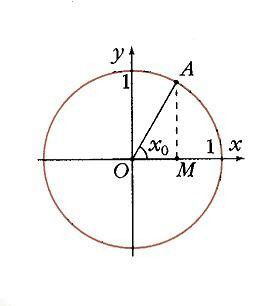
Функция у = cos х.
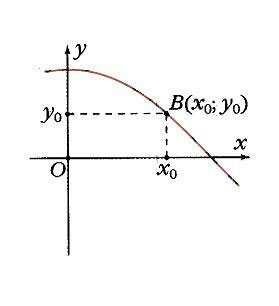
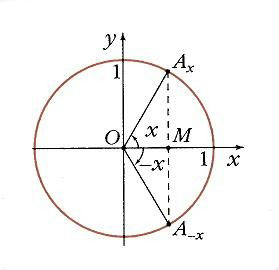
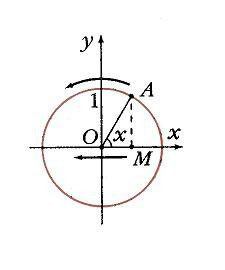
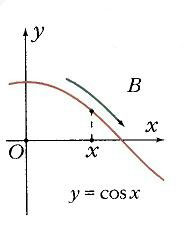
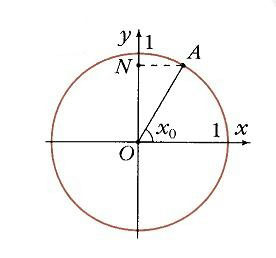
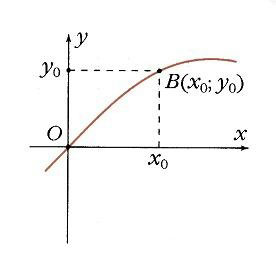
Если построить единичную окружность с центром в начале координат, и задать произвольное значение аргумента x0 и отсчитать от оси Ox угол x0, то этому углу на единичной окружности соответствует некоторая точка A (рис. 1) а ее проекцией на ось Ох будет точка М. Длина отрезка ОМ равна абсолютной величине абсциссы точки A. Данному значению аргумента x0 сопоставлено значение функции y = cos x0 как абсциссы точки А. Соответственно точка В (x0; у0) принадлежит графику функции у = cos х (рис. 2). Если точка А находится правее оси Оу, то косинус будет положителен, если же левее – отрицателен. Но в любом случае точка А не может покинуть окружность. Поэтому косинус лежит в пределах от –1 до 1:
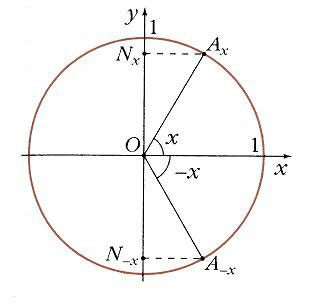
Если взять два значения аргумента, равные по абсолютной величине, но противоположные по знаку, x и –x, найти на окружности соответствующие точки Ax и А-x. Как видно на рис. 3 их проекцией на ось Ох является одна и та же точка М. Поэтому
Значит, можно исследовать свойства функции y = cos х на отрезке [0, p ], а затем учесть ее четность и периодичность.
Функция y = sin х.
На единичной окружности углу x0 соответствует точка А (рис. 7), а ее проекцией на ось Оу будет точка N. Значение функции у0 = sin x0 определяется как ордината точки А. Точка В (угол x0, у0) принадлежит графику функции y = sin x (рис. 8). Ясно, что функция y = sin x периодическая, ее период равен 2 p :
т.е. синус – функция нечетная, f(–x) = –f(x) (рис. 9).
Если точку A повернуть относительно точки О на угол p /2 против часовой стрелки (другими словами, если угол х увеличить на p /2), то ее ордината в новом положении будет равна абсциссе в старом. А значит,
Иначе, синус – это косинус, «запоздавший» на p /2, поскольку любое значение косинуса «повторится» в синусе, когда аргумент возрастет на p /2. И чтобы построить график синуса, достаточно сдвинуть график косинуса на p /2 вправо (рис. 10). Чрезвычайно важное свойство синуса выражается равенством
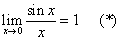
Геометрический смысл равенства виден из рис. 11. Здесь х – это половина дуги АВ, а sin х – половина соответствующей хорды. Очевидно, что по мере сближения точек А и В длина хорды все точнее приближается к длине дуги. Из того же рисунка несложно извлечь неравенство
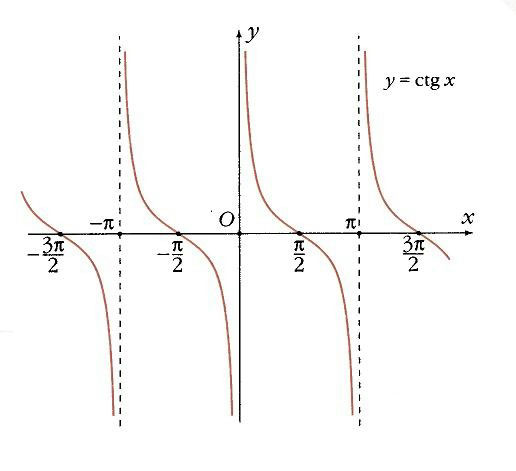
Функции у = tg х, у = ctg х. Две другие тригонометрические функции – тангенс и котангенс проще всего определить как отношения уже известных нам синуса и косинуса:
Котангенс не определен там, где синус равен 0 (когда х = k p ). В остальных точках он монотонно убывает, а прямые х = k p – его вертикальные асимптоты. В точках х = p /2 + k p котангенс обращается в 0, а угловой коэффициент в этих точках равен –1 (рис. 13).
Четность и периодичность.
Функция называется четной, если f(–x) = f(x). Функции косинус и секанс – четные, а синус, тангенс, котангенс и косеканс – функции нечетные:
| sin (–α) = – sin α | tg (–α) = – tg α |
| cos (–α) = cos α | ctg (–α) = – ctg α |
| sec (–α) = sec α | cosec (–α) = – cosec α |
| sin (α + 2kπ) = sin α | cos (α + 2kπ) = cos α |
| tg (α + kπ) = tg α | ctg (α + kπ) = ctg α |
| sec (α + 2kπ) = sec α | cosec (α + 2kπ) = cosec α |
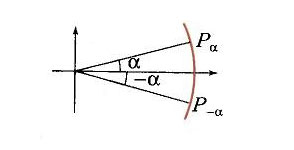
Периодичность синуса и косинуса следует из того, что все точки P a + 2k p , где k = 0, ±1, ±2,…, совпадают, а периодичность тангенса и котангенса – из того, что точки P a + k p поочередно попадают в две диаметрально противоположные точки окружности, дающие одну и ту же точку на оси тангенсов.
Основные свойства тригонометрических функций могут быть сведены в таблицу:
Формулы приведения.
 – a
– a + a
+ a + a
+ a + a
+ a1) название функции сохраняется, если k четное, и меняется на «дополнительное», если k нечетное;
Формулы сложения.
sin ( a 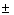
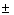
cos ( a 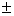
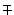
Формулы кратных углов.
Эти формулы выводятся прямо из формул сложения:
sin 2 a = 2 sin a cos a ;
cos 2 a = cos 2 a – sin 2 a = 2 cos 2 a – 1 = 1 – 2 sin 2 a ;
sin 3 a = 3 sin a – 4 sin 3 a ;
cos 3 a = 4 cos 3 a – 3 cos a ;
Если в формулах двойного аргумента заменить a на a /2, их можно преобразовать в формулы половинных углов:
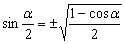
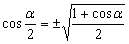
Формулы универсальной подстановки.
Используя эти формулы, выражение, включающее разные тригонометрические функции от одного и того же аргумента, можно переписать как рациональное выражение от одной функции tg ( a /2), это бывает полезно при решении некоторых уравнений:
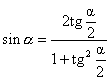 | 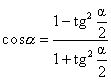 |
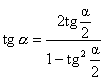 | 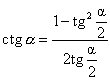 |
Формулы преобразования сумм в произведения и произведений в суммы.
До появления компьютеров эти формулы использовались для упрощения вычислений. Расчеты производились с помощью логарифмических таблиц, а позже – логарифмической линейки, т.к. логарифмы лучше всего приспособлены для умножения чисел, поэтому все исходные выражения приводили к виду, удобному для логарифмирования, т.е. к произведениям, например:
2 sin a sin b = cos ( a – b ) – cos ( a + b );
2 cos a cos b = cos ( a – b ) + cos ( a + b );
2 sin a cos b = sin ( a – b ) + sin ( a + b ).
Формулы для функций тангенса и котангенса можно получить из вышеприведенных.
Формулы понижения степени.
Из формул кратного аргумента выводятся формулы:
| sin 2 a = (1 – cos 2 a )/2; | cos 2 a = (1 + cos 2 a )/2; |
| sin 3 a = (3 sin a – sin 3 a )/4; | cos 3 a = (3 cos a + cos 3 a )/4. |
С помощью этих формул тригонометрические уравнения можно приводить к уравнениям более низких степеней. Таким же образом можно вывести и формулы понижения для более высоких степеней синуса и косинуса.
| Производные и интегралы тригонометрических функций | |
| (sin x)` = cos x; | (cos x)` = –sin x; |
(tg x)` = 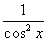 ; ; | (ctg x)` = – 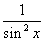 ; ; |
| т sin x dx = –cos x + C; | т cos x dx = sin x + C; |
| т tg x dx = –ln |cos x| + C; | т ctg x dx = ln |sin x| + C; |
Каждая тригонометрическая функция в каждой точке своей области определения непрерывна и бесконечно дифференцируема. Причем и производные тригонометрических функций являются тригонометрическими функциями, а при интегрировании получаются так же тригонометрические функции или их логарифмы. Интегралы от рациональных комбинаций тригонометрических функций всегда являются элементарными функциями.
Представление тригонометрических функций в виде степенных рядов и бесконечных произведений.
Все тригонометрические функции допускают разложение в степенные ряды. При этом функции sin x b cos x представляются рядами. сходящимися для всех значений x:
Эти ряды можно использовать для получения приближенных выражений sin x и cos x при малых значениях x:
Функции sin x и cos x могут быть представлены в виде бесконечных произведений:
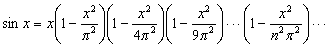
Тригонометрические функции комплексного аргумента
определяются как аналитические продолжения соответствующих тригонометрических функций действительного аргумента в комплексную плоскость. Так, sin z и cos z могут быть определены с помощью рядов для sin x и cos x, если вместо x поставить z:
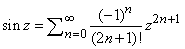
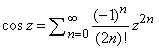
Эти ряды сходятся по всей плоскости, поэтому sin z и cos z – целые функции.
Тангенс и котангенс определяются формулами:
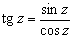
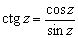
Функции tg z и ctg z – мероморфные функции. Полюсы tg z и sec z – простые (1-го порядка) и находятся в точках z = p /2 + p n, полюсы ctg z и cosec z – также простые и находятся в точках z = p n, n = 0, ±1, ±2,…
Все формулы, справедливые для тригонометрических функций действительного аргумента, справедливы и для комплексного. В частности,
т.е. четность и нечетность сохраняются. Сохраняются и формулы
т.е. периодичность также сохраняется, причем периоды такие же, как и для функций действительного аргумента.
Тригонометрические функции могут быть выражены через показательную функцию от чисто мнимого аргумента:
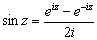
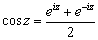
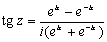
Обратно, e iz выражается через cos z и sin z по формуле:
Эти формулы носят название формул Эйлера. Леонард Эйлер вывел их в 1743.
Тригонометрические функции также можно выразить через гиперболические функции:
z = –i sh iz, cos z = ch iz, z = –i th iz.
где sh, ch и th – гиперболические синус, косинус и тангенс.
Тригонометрические функции комплексного аргумента z = x + iy, где x и y – действительные числа, можно выразить через тригонометрические и гиперболические функции действительных аргументов, например:
Синус и косинус комплексного аргумента могут принимать действительные значения, превосходящие 1 по абсолютной величине. Например:
Если неизвестный угол входит в уравнение как аргумент тригонометрических функций, то уравнение называется тригонометрическим. Такие уравнения настолько часто встречаются, что методы их решения очень подробно и тщательно разработаны. С помощью различных приемов и формул тригонометрические уравнения сводят к уравнениям вида f(x) = a, где f – какая-либо из простейших тригонометрических функций: синус, косинус, тангенс или котангенс. Затем выражают аргумент x этой функции через ее известное значение а.
Поскольку тригонометрические функции периодичны, одному и тому же а из области значений отвечает бесконечно много значений аргумента, и решения уравнения нельзя записать в виде одной функции от а. Поэтому в области определения каждой из основных тригонометрических функций выделяют участок, на котором она принимает все свои значения, причем каждое только один раз, и находят функцию, обратную ей на этом участке. Такие функции обозначают, приписывая приставку агс (дуга) к названию исходной функции, и называют обратными тригонометрическими функциями или просто аркфункциями.
Обратные тригонометрические функции.
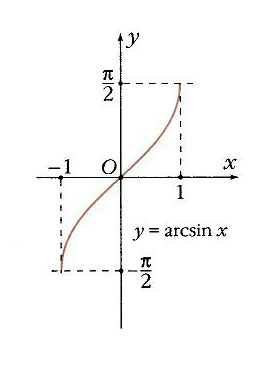
Для sin х, cos х, tg х и ctg х можно определить обратные функции. Они обозначаются соответственно arcsin х (читается «арксинус x»), arcos x, arctg x и arcctg x. По определению, arcsin х есть такое число у, что
Аналогично и для других обратных тригонометрических функций. Но такое определение страдает некоторой неточностью.
Если отразить sin х, cos х, tg х и ctg х относительно биссектрисы первого и третьего квадрантов координатной плоскости, то функции из-за их периодичности становятся неоднозначными: одному и тому же синусу (косинусу, тангенсу, котангенсу) соответствует бесконечное количество углов.
Так же решаются другие простейшие тригонометрические уравнения:
где п = 0, ±1, ±2. (рис. 16);
где п = 0, ±1, ±2. (рис. 17);
где п = 0, ±1, ±2. (рис. 18).
Основные свойства обратных тригонометрических функций:
arcsin х (рис. 19): область определения – отрезок [–1, 1]; область значений – [– p /2, p /2], монотонно возрастающая функция;
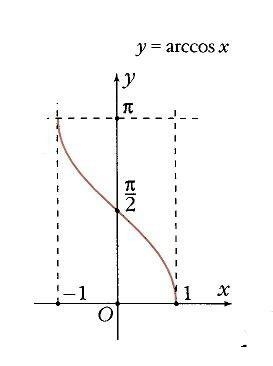
arccos х (рис. 20): область определения – отрезок [–1, 1]; область значений – [0, p ]; монотонно убывающая функция;
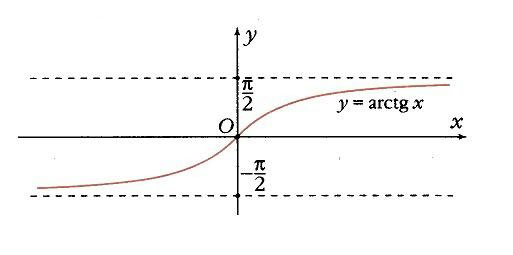
arctg х (рис. 21): область определения – все действительные числа; область значений – интервал (– p /2, p /2); монотонно возрастающая функция; прямые у = – p /2 и у = p /2 – горизонтальные асимптоты;
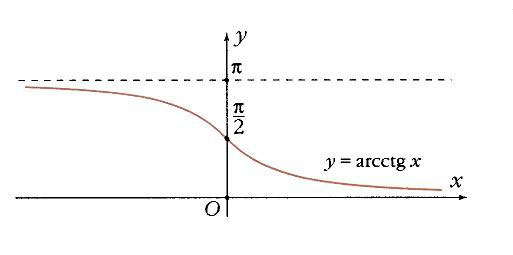
arcctg х (рис. 22): область определения – все действительные числа; область значений – интервал (0, p ); монотонно убывающая функция; прямые y = 0 и у = p – горизонтальные асимптоты.
Т.к. тригонометрические функции комплексного аргумента sin z и cos z (в отличие от функций действительного аргумента) принимают все комплексные значения, то и уравнения sin z = a и cos z = a имеют решения для любого комплексного a:
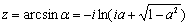
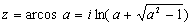
Функции tg z и ctg z принимают все комплексные значения, кроме ±i: уравнения tg z = a, ctg z = a имеют решения для любого комплексного числа a № ± i:
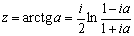
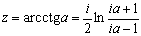
Для любого z = x + iy, где x и y – действительные числа, имеют место неравенства
из которых при y ® Ґ вытекают асимптотические формулы (равномерно относительно x)
Кочетков Е.С., Кочеткова Е. С. Алгебра и элементарные функции, ч. 1–2, М., 1966
Шабат Б.В. Введение в комплексный анализ. М., 1969