что такое три квадрата
Что такое три квадрата
Таинственное название «Три квадрата» интригует читателя уже само по себе. И правильно делает, что интригует, потому что обозначает оно, неожиданным образом, издательство интеллектуальной литературы. Совсем небольшое и с невеликими тиражами. Тихая такая культурная работа, без которой, однако, наш смысловой ландшафт, пожалуй, был бы в заметной степени другим.
А ещё их интересует история русского авангарда. А ещё…
Ольга Балла: Сергей Васильевич, давайте для начала обозначим вашу культурную нишу. В чём состоял замысел издательства, его первоначальная программа – и менялась ли она со временем? Кто был инициатором его создания?
Конкретной же программы у нас поначалу будто бы и не было. Были конкретные авторы очень хорошего уровня, в том числе пришедшие из общения в сети, были серьезные заказчики. Подтолкнул же нас к созданию собственного дела наш друг Сергей Гитман – замечательный фотограф и переводчик. Он даже предложил на организацию издательства денег взаймы – насколько помню, все затраты на оформление предприятия обошлись тогда в скромные 300-400 долларов.
О.Б.: Поначалу программы не было – но позже она ведь как-то обозначилась?
С.М.: Если считать «гуманитарность» не только набором дисциплин, но и производным от слов «гуманность, гуманизм» – разве это нельзя назвать программой? Помимо чисто российских, у нас множество международных проектов, работающих на взаимообогащение культур. Особое удовлетворение доставляют издания, в которых зарубежные исследователи изучают или пропагандируют реалии нашей культуры или отечественные авторы вносят существенную лепту в исследование интернациональной проблематики.
О.Б.: А что означает название «Три квадрата»? Признаюсь, у меня было предположение, что это три основные тематические области издательства: философия, изобразительное искусство (включая архитектуру) и литература.
О.Б.: Оно небольшое в смысле тиражей, количества наименований, количества сотрудников или всего этого вместе? Это был сознательный выбор – сделать его таким?
О.Б.: К каким читателям вы адресуетесь?
С.М.: К очень разным. Обычно мы говорим: наши книги «для подготовленного читателя». Я быстро понял, что у публикаций по русской и по немецкой философии аудитории не совпадают. Что касается истории, театра, изданий по народному искусству, искусству авангарда и т.д. – тут то же самое.
Проблема для издателя состоит в том, что путь книги к читателю каждый раз надо выстраивать заново. Так, мы сознательно заранее планируем невысокую отпускную цену на серию альбомов по музеям российской провинции, поскольку понимаем, что часть тиража идет «в глубинку», а там народ очень небогатый. Кроме того, довольно часто приходится помнить о читателе зарубежном. Отсюда присутствие в наших изданиях английского (хотя бы в подписях, заголовках и резюме).
Серия прервалась по организационным и экономическим причинам, но, надеюсь, она вот-вот должна возродиться – сейчас мы работаем над этим с друзьями в Будапеште.
О.Б.: Чем заинтересовала ваше издательство венгерская культура? Кто (или что) оказался в ней для вас открытием?
С.М.: Я бы сказал, интенсивностью интеллектуального драйва, большим количеством прекрасных музыкантов, поэтов, художников, ученых на душу населения. Открытий тут было очень много, и они продолжаются. Но в первую очередь я бы назвал Илону Киш, бывшего директора Культурного центра Венгрии в Москве, которая в годы своей работы превратила его в одно из самых популярных мест в нашем городе, а также Акоша Силади – поэта и философа, ставшего составителем нашей венгерской серии. Именно они открыли для России новые интересные имена.
О.Б.: Ещё хотелось бы услышать подробнее о серии «Архитектурное наследие в фотографиях». По какому принципу отбираются города, которые будут в ней представлены?
Кстати, кроме упомянутой серии, была еще серия «вологодская» (шесть объемных томов в переплетах) и целый ряд совместных научных сборников, где Брумфилд был или составителем, или участником. А первым изданием Брумфилда у нас стал каталог его фотовыставки в Государственном архитектурном музее в 2001 или 2002 году. Так что общее число его изданий – свыше двадцати пяти.
О.Б.: Что вы вообще считаете вашими издательскими удачами?
С.М.: Скажу лучше, что считаю неудачами: как правило, это те случаи, когда уважаемый мной автор игнорирует наш издательский опыт и стратегию и «продавливает» свое представление о будущем издании. Самое плодотворное сотрудничество – когда нам доверяют.
О.Б.: Кого можно назвать в числе ваших самых ярких авторов? И что было лично вам наиболее симпатично и важно среди изданного?
С.М.: Что касается имен, то их очень много. Если в хронологическом порядке, то надо начать с Гасана Гусейнова с его великим словарем 1990-х [11], с Елены Петровской [12]. Если, так сказать, «по ранжиру», то это нобелевский лауреат Имре Кертес [13], Евгений Пастернак с его воспоминаниями об отце [14], Юрий Любимов [15] и многие другие. Это наши американские авторы, пишущие о русском зодчестве – упомянутый уже автор многочисленных фотоальбомов Уильям Брумфилд – или об авангарде – Шарлотта Дуглас (предисловие к ее книге «Лебеди иных миров и другие статьи об авангарде» [16] написал Дмитрий Сарабьянов). Были и совсем личные проекты, как бы выплывшие из моей юности: Борис Пильняк [17], Мохой-Надь.
О.Б.: Были ли книги, которые прошли менее замеченными, чем, по вашему разумению, стоило бы, и с чем вы это связываете?
Книга получилась очень красивая и информативная – много интересного даже для тех, кто занимается лермонтовской эпохой. Но мое разочарование заключается в том, что, несмотря на чрезвычайно теплое письмо Президента Республики Дагестан Рамазана Абдулатипова с идеей приобрести для библиотек республики половину тиража, дело так ничем и не кончилось. Понимаю: экономика. Что же касается московского и питерского читателя, он, видимо, сосредоточен на своих, более близких проблемах. Поэтому книгой заинтересовались в основном специалисты-этнографы да художники, знавшие чудесную Катю Григорьеву.
О.Б.: Вообще, в какой мере вы находите востребованным и услышанным ваше издательское послание?
С.М.: Собственно говоря, есть два измерения востребованности для такой малотиражной литературы, как нон-фикшн. Первый критерий: распродан ли тираж и как быстро. Второй: в каких библиотеках мира появилась ваша книга.
Сейчас мы работаем над расширением нашей серии «Художественные сокровища российской провинции», готовим уже шестой выпуск – о коллекциях Сергиево-Посадского музея игрушек. За этими книгами, можно сказать, охотятся научные сотрудники музеев, там множество первых публикаций, есть просто открытия. Ресурс этой серии очень большой – об этом говорят и музейщики, и коллекционеры. Предыдущие выпуски лежат во многих зарубежных библиотеках и музеях – например, в музее Метрополитен. Надо с этим работать и дальше.
О.Б.: Невозможно противостоять соблазну спросить о планах, проектах и мечтаниях. Каковы же они?
1. Русский фотограф на рубеже эпох. – М., 2015.
10. Ласло Мохой-Надь и русский авангард. – М., 2006.
11. Гасан Гусейнов. ДСП: Материалы к русскому словарю общественно-политического языка. – Т. 1-2. – М., 2003; Он же. Советские идеологемы в русском дискурсе 1990-х. — М., 2003.
12. Помимо журнала «Синий диван», это – книга «Антифотография» (М., 2003; 2-е дополненное издание – 2015.)
13. Кертес Имре. Язык в изгнании: Статьи и эссе. – М., 2004.
14. Евгений Пастернак. Понятое и обретенное: статьи и мемуары. – М., 2009
15. Юрий Любимов. 80 лет в мировом сценическом искусстве: альбом. – М., 2014.
17. Пильняк Борис. Корни японского солнца. – М., 2004.
Таблица квадратов
Таблица квадратов или таблица возведения чисел во вторую степень. Интерактивная таблица квадратов и изображения таблицы в высоком качестве.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 |
| 1 | 100 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 |
| 2 | 400 | 441 | 484 | 529 | 576 | 625 | 676 | 729 | 784 | 841 |
| 3 | 900 | 961 | 1024 | 1089 | 1156 | 1225 | 1296 | 1369 | 1444 | 1521 |
| 4 | 1600 | 1681 | 1764 | 1849 | 1936 | 2025 | 2116 | 2209 | 2304 | 2401 |
| 5 | 2500 | 2601 | 2704 | 2809 | 2916 | 3025 | 3136 | 3249 | 3364 | 3481 |
| 6 | 3600 | 3721 | 3844 | 3969 | 4096 | 4225 | 4356 | 4489 | 4624 | 4761 |
| 7 | 4900 | 5041 | 5184 | 5329 | 5476 | 5625 | 5776 | 5929 | 6084 | 6241 |
| 8 | 6400 | 6561 | 6724 | 6889 | 7056 | 7225 | 7396 | 7569 | 7744 | 7921 |
| 9 | 8100 | 8281 | 8464 | 8649 | 8836 | 9025 | 9216 | 9409 | 9604 | 9801 |
Таблица квадратов
Теория
Квадрат числа – это результат умножения числа само на себя. Операция вычисления квадрата числа – это частный случай возведения числа в степень, в данном случае во вторую:
Данное выражение читается: «возвести в квадрат число 6» или «6 в квадрате».
Скачать таблицу квадратов
Логические задачи и головоломки
С помощью шести спичек построить три одинаковых квадрата. Требуется немного нестандартного мышления.
Ответ: Извините за то, что ответ выглядит несколько издевательски, но мы ведь не говорили, что нельзя ломать спички.
Комментарии
браво 37 я тож также решил. А вообще как было замечено чтоб не чуствовать себя идиотом. Следовало бы в задачу вводит доп требования например Квадраты д.быть Максимальны по площади!
браво 37 я тож также решил. А вообще как было замечено чтоб не чуствовать себя идиотом. Следовало бы в задачу вводит доп требования например Квадраты д.быть Максимальны по площади!
Хотя Забавно-с. наши-то с тобой придумки По параметру площадь нисколько не уступают квадратам приведённым в решении.
А Вот по параметру материалоёмкость, и трудоёмкость выглядят даже более выиграшно.Т.к. экономят в сумме целую спичку. Слава Горбачёву М.С. «Экономика должна быть экономной»
а вы попробуйте, не ломая, из 6 спичек сложить 4 одинаковых треугольника.
Согласен. Но вы ведь не говорили, что нельзя накладывать спички друг на друга, и чтобы концы спичек не торчали. Вот решение:
Не ломая, но накладывая:
Кладем 4 спички параллельно друг другу (IIII)? расстояние между ними должно составлять 0,25% от длины спички.
Двумя оставшимися спичками пересекаем, указанные 4 (=), при этом расстояние между этими двумя также 0,25% от длины спички.
В итоге получаем сетку, внутри которой 3 одинаковых квадрата.
P.s. Не подумайте, я не пол года думал. просто открыл этот ресурс для себя пару дней назад и только сейчас дошел до этой задачи.
Ошибочка. Не 0,25%, а треть от длины спички.
Если сломать все спички пополам, любой олигофрен сможет построить!
Прямоугольный параллелепипед. Что это такое?
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение параллелепипеда
Начнем с того, что узнаем, что такое параллелепипед.
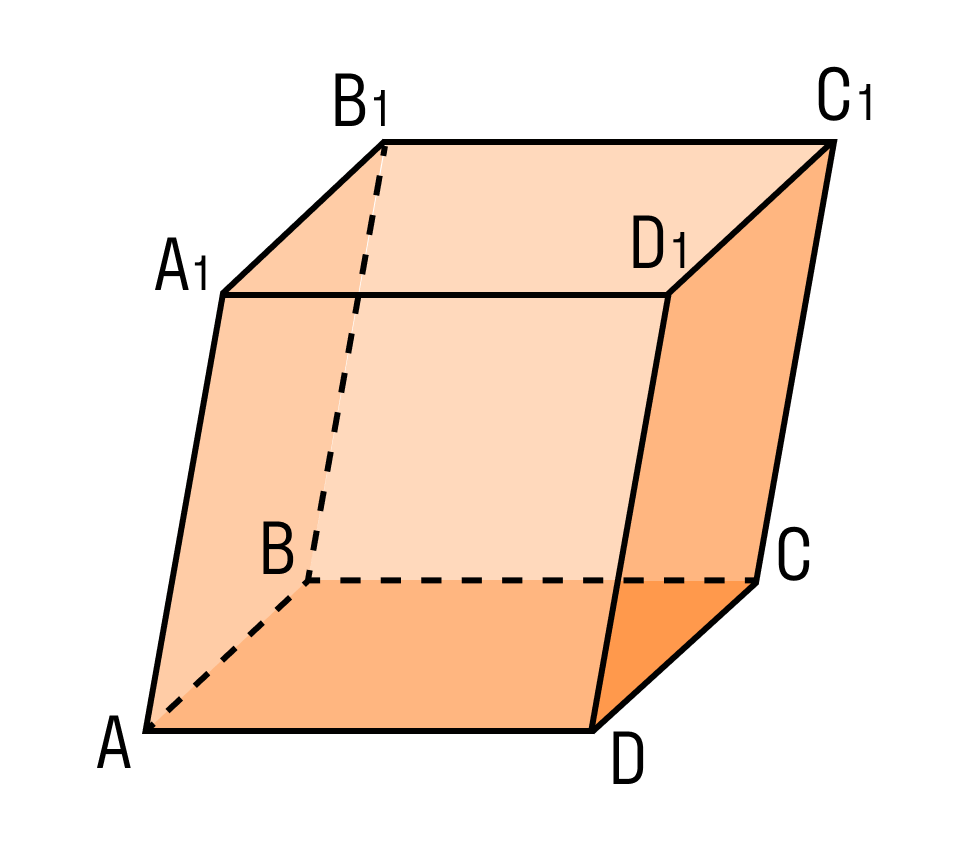
Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.
На рисунке два параллелограмма АВСD и A1B1C1D1. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA1, ВB1, CC1, DD1 параллельны друг другу. Образовавшаяся фигура — параллелепипед.
Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.
Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.
Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.
Параллелепипед — это:
Правильный параллелепипед на то и правильный, что два его измерения равны. Две грани такого правильного параллелепипеда — квадраты.
Свойства параллелепипеда
Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.
Вот 4 свойства параллелепипеда, которые необходимо запомнить:
Прямой параллелепипед
Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.
Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.
Свойства прямого параллелепипеда:
На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.
Формулы прямого параллелепипеда:
Прямоугольный параллелепипед
Определение прямоугольного параллелепипеда:
Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.
Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.
Свойства прямоугольного параллелепипеда
Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.
Формулы прямоугольного параллелепипеда:
Диагонали прямоугольного параллелепипеда: теорема
Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.
Если есть теорема, нужно ее доказать. (с) Пифагор
Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.
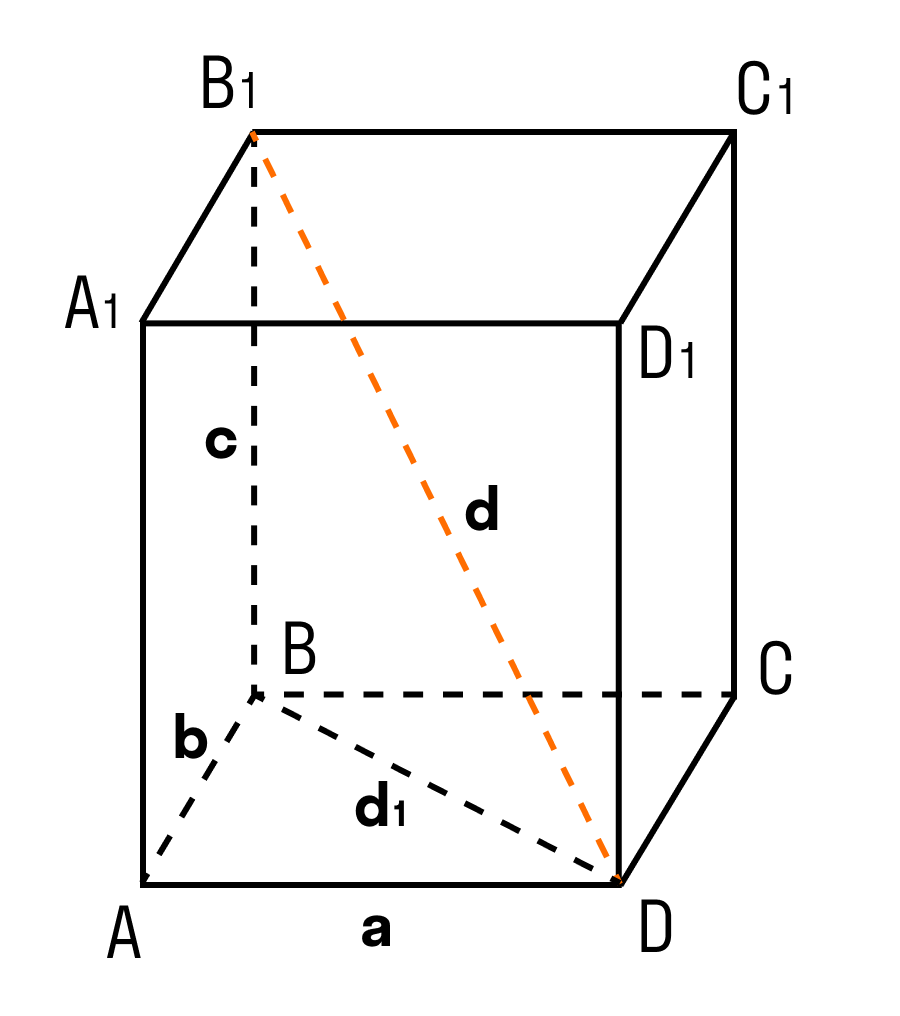
Дан прямоугольный параллелепипед ABCDA1B1C1D1. Доказать теорему.
Доказательство теоремы:
Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.
Все грани прямоугольного параллелепипеда — прямоугольники.
ΔABD: ∠BAD = 90°, по теореме Пифагора
ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора
d² = a² + b² + c²
Доказанная теорема — пространственная теорема Пифагора.
У нас есть отличные дополнительные онлайн занятия по математике для учеников с 1 по 11 классы, записывайся!
Куб: определение, свойства и формулы
Кубом называется прямоугольный параллелепипед, все три измерения которого равны.
Каждая грань куба — это квадрат.
Свойства куба:
Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.
Формулы куба:
Решение задач
Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.
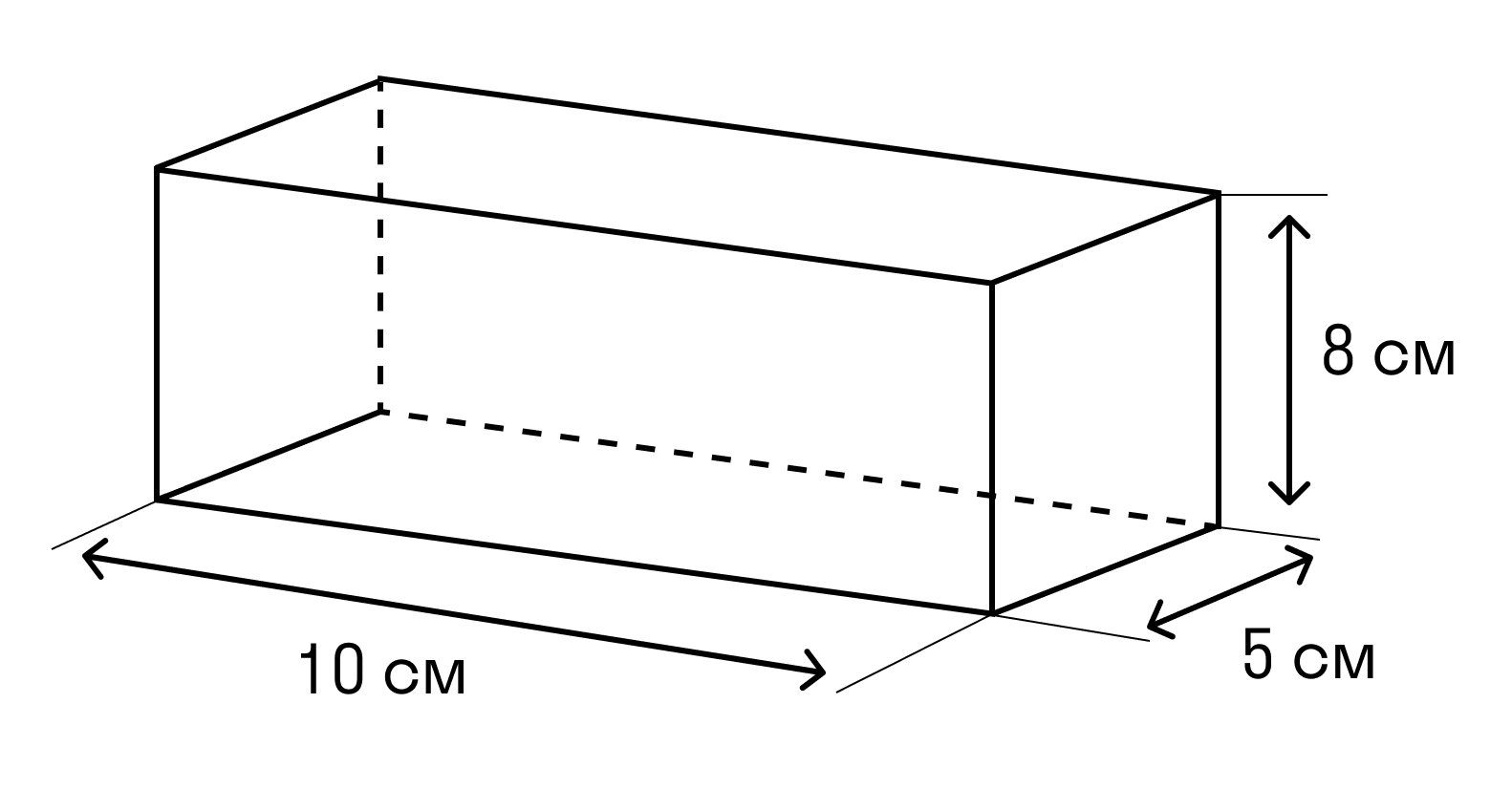
Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.
Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.
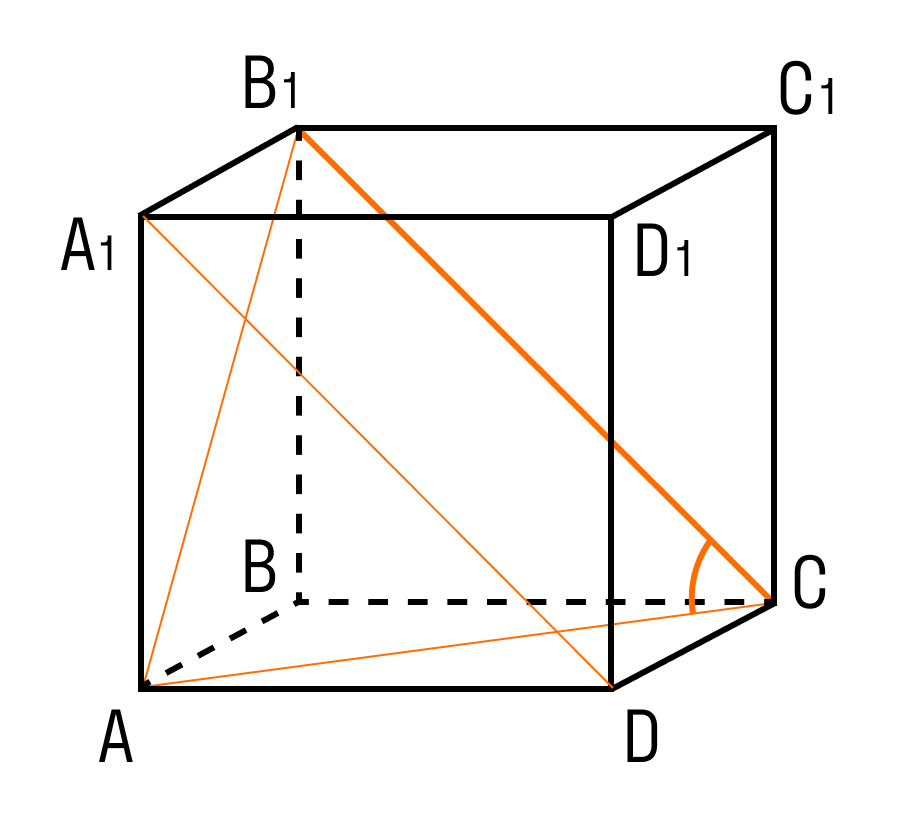
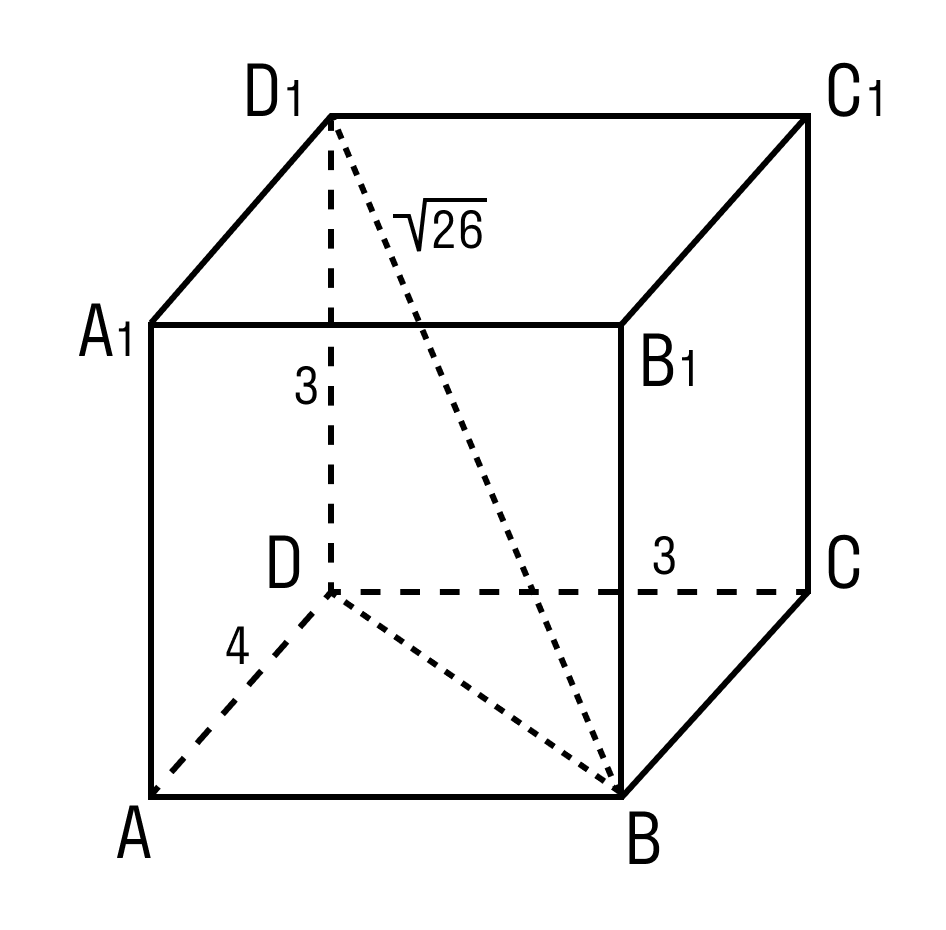
Задачка 2. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
Нужно найти длину ребра A1B1.
В фокусе внимания треугольник BDD1.
Угол D = 90°. Против равных сторон лежат равные углы.
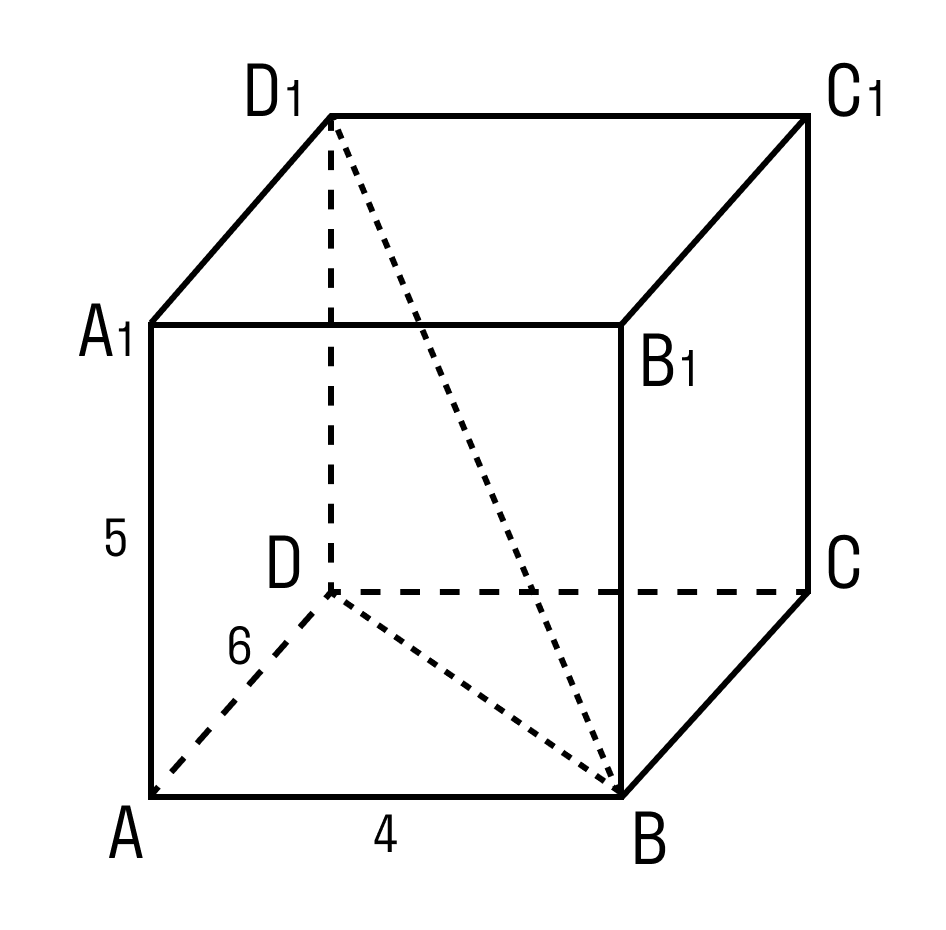
Задачка 3. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
AB = 4
AD = 6
AA1= 5
Нужно найти отрезок BD1.
В треугольнике ADB угол A = 90°.
По теореме Пифагора:
BD 2 = AB 2 +AD 2
BD 2 = 4 2 + 6 2 = 16 + 36 = 52
В треугольнике BDD1 угол D = 90°.
BD1 2 = 52 + 25 = 77.
Самопроверка
Теперь потренируйтесь самостоятельно — мы верим, что все получится!
Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.
Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.
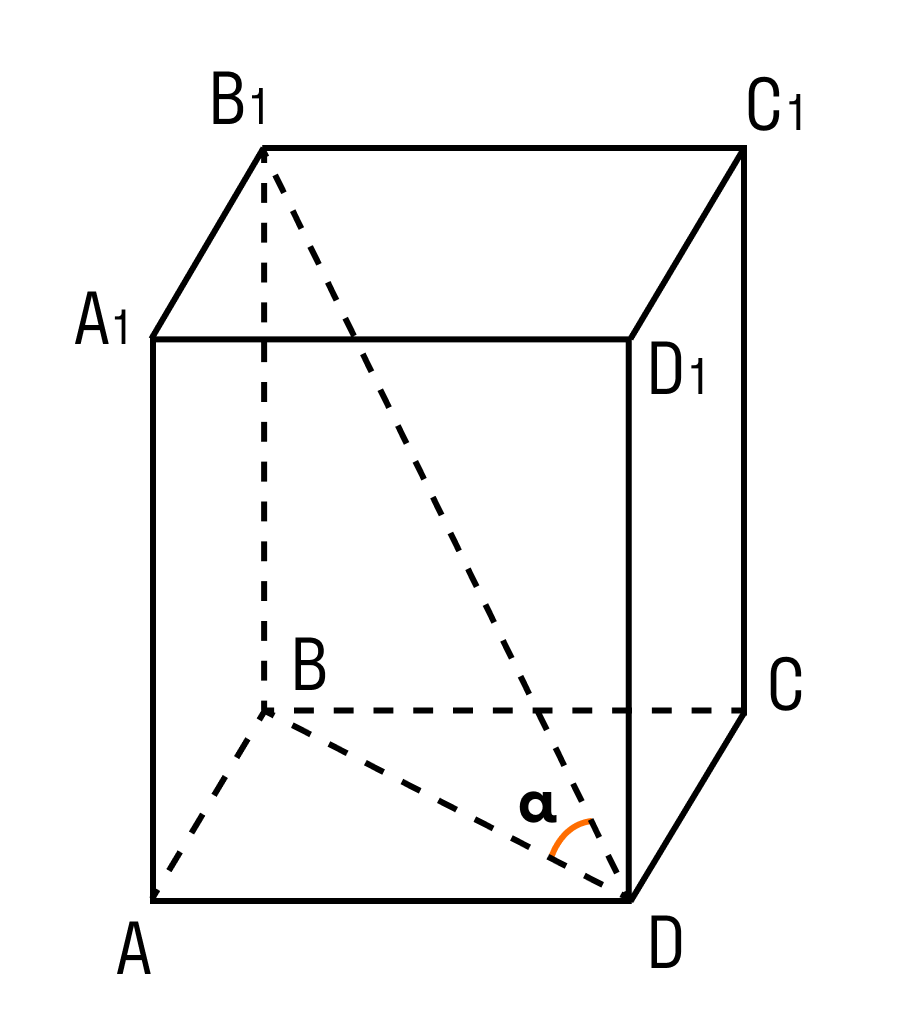
Задачка 2. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
Вычислите длину ребра AA1.
Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий: