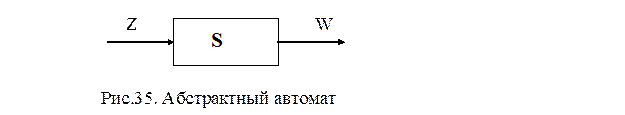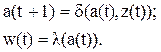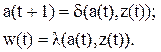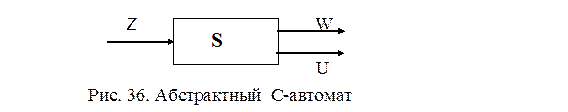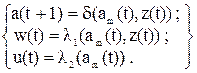Теория вычислений. Введение в конечные автоматы

Это до предела упрощенная модель компьютера имеющая конечное число состояний, которая жертвует всеми особенностями компьютеров такие как ОЗУ, постоянная память, устройства ввода-вывода и процессорными ядрами в обмен на простоту понимания, удобство рас­суждения и легкость программной или аппаратной реализации.

С помощью КА можно реализовать такие вещи как, регулярные выражения, лексический анализатор, ИИ в играх и тд.

У конечных автоматов имеется таблица переходов, текущее состояние автомата, стартовое состояние и заключительное состояние.

Таблица переходов — В ней хранятся переходы для текущего состояния и входного символа. Простейшая реализация может быть как двумерный массив.

Здесь видно, что из состояния 0 в состояние 1 можно попасть только, если у нас будет входной символ ‘a’, из состояния 1 в состояние 2, если символ ‘b’.

Текущее состояние — множество состояний в котором автомат может находиться в данный момент времени.

Стартовое состояние — состояние откуда КА начинает свою работу.

Заключительное состояние — множество состояний в которых автомат принимает определенную цепочку символов, в ином случае отвергает.

Детерминированные конечные автоматы (deterministic finite automaton)

Простейший КА, в котором может быть одно состояние в текущий момент времени, обладает детерминированностью.

Детерминированность — для всех состояний имеется максимум и минимум одно правило для любого возможного входного символа, то есть например, для состояния 1 не может быть два перехода с одним и тем же входным символом.

Недетерминированные конечные автоматы (nondeterministic finite automaton)

НКА не является каким-то существенным улучшением ДКА, просто в нем добавлен так сказать синтаксический сахар, в виде свободных переходов, недетерминированности и множеств состояний. Реализовать можно как массив состоящий из структур в которой хранится состояние, входной символ и следующее состояние.

Свободные переходы (эпсилон переходы) — переходы, которые можно совершать без чтения входного символа.

Недетерминированность — ноль и более переходов для одного символа в каких-либо состояниях.

Множества состояний — в один момент времени НКА может находится в нескольких состояниях.

Заключительное состояние обозначается двойным кругом.

В стартовом состоянии у нас текущим состоянием является <1>, при входном символе ‘b’ у нас появляется возможность, пойти в состояние 1 и в состояние 2, то есть после входного символа ‘b’ текущим состоянием является множество <1, 2>.

Свободным переходом обозначается пунктирной линией.

Здесь видно два свободных перехода из стартового состояния, то есть без чтения входного символа мы сразу находимся в множестве состоянии <2, 4>.

Для преобразования НКА в ДКА используется алгоритм Томпсона.
При преобразовании НКА в ДКА может получиться не совсем минимальный ДКА и для его минимизации можно применить алгоритм Бржозовского.

Конечные автоматы с магазинной памятью (pushdown automaton)

Это тот же КА, но с дополнительной памятью в виде стека. Теперь для совершения перехода нужно учитывать еще несколько факторов, символ который нужно удалить из стека и символы которые нужно добавить в стек.

КАМП можно применять в таких местах, где может быть неограниченное количество вложений, например при разборе языков программирование или подсчету вложенных скобок в математических выражениях. Реализовать с помощью КА невозможно, ведь количество возможных состояний конечно в отличие от стека (я понимаю, что память тоже конечна).

Удаление символа из стека — при любом переходе решается какой символ вытолкнуть, если на вершине стека не оказалось такого символа, то он и не выталкивается. Так же если символ нужно оставить в стеке, то он добавляется вместе с добавляемыми символами.

Добавление символов в стек — при любом переходе решает какие символы добавить в стек.

Этот КАМП подсчитывает вложенность скобок, за счет добавления и удаления символов из стека.

ДАМП не равен НАМП, поэтому невозможно одно преобразовать в другое, следовательно НАМП обладает преимуществом перед ДАМП.

Машина Тьюринга (Turing machine)

Самая мощная машина из существующих, его преимущество перед другими в ленте с которой он может работать как хочет. В нем нет свободных переходов. Умеет интерпретировать другие автоматы такие как КА, КАМП.

Лента — это одномерный массив в который могут записываться данные за счет головки над ячейкой, который можно заранее заполнить входными данными.

Шаблон: считаный_символ_с_головки/записаный_символ; сторона_смещения_головки. края ленты обозначаются ‘_’.

Эта МТ выполняет инкремент двоичного числа, головка стоит слева, там где начинается лента.

ДМТ эквивалентен НМТ, так, что они тоже не различаются.

Универсальная машина Тьюринга (universal Turing machine)

Машина которая может порождать другие машины Тьюринга, получая на входную ленту данные машины.

Источник

Теория автоматов: определение, элементы, применение и примеры

Теория автоматов — это область дискретной математики, которая изучает специальны е «абстрактные автоматы». Абстрактный автомат — это вычислительная машина, которая представлена в виде специальной математической модели. А для человека он может выглядеть как вычислительное устройство, выполняющее последовательность запрограммированных операций.

Теория автоматов применяется в направлении информатики и вычислительной техники. Она имеет широкую сферу применения в этом направлении. Например:

Участвует в проектировании систем с логическим управлением.

Помогает обрабатывать тексты и проектировать компиляторы.

Обеспечивает спецификацию и верификацию взаимодействующих процессов.

Участвует в написании документации к программам, написанным на объектно-ориентированных языках.

Участвует в оптимизации логических программ.

Теория автоматов

Теория автоматов — сложная вещь, но мы постараемся рассказать о ней простыми словами. Итак, теория автоматов — это научная область, изучающая абстрактные автоматы. Абстрактный автомат описывает разные состояния автоматов. Одно из таких состояний — это конечный автомат.

По сути, к онечный автомат — это очень сильно упрощенное компьютерное устройство, в котором прописаны определенные состояния и количество этих состояний. В конечных автоматах отсутству ю т:

средства для ввода или вывода,

процессорные ядра и др.

Пожертвовав всеми характеристиками компьютера, конечный автомат обладает:

программной простотой и легкостью,

упрощенной аппаратной реализацией,

способностью внедрять удобные логические рассуждения и др.

Конечный автомат характеризуется 4-мя свойствами:

Таблица переходов. Это таблица, в которой хранятся вероятные переходы, зависящие от текущего состояния конечного автомата.

Текущее состояние. Это набор состояний, в которых может располагаться конечный автомат в конкретный функциональный момент.

Стартовое состояние — момент, с которого конечный автомат активирует собственную деятельность.

Заключительное состояние — момент, который может состоять из нескольких состояний, в которых конечный автомат заканчивает свою работу.

Детерминированный и недетерминированный конечный автомат

Конечный автомат может быть 2-х типов:

Детерминированный конечный автомат. Это конечный автомат, который имеет определенное число состояний. Для каждого отдельного состояния определен входной символ. Такой автомат в конкретный момент времени может располагаться в единственном состоянии. Детерминированный конечный автомат обычно представляет собой простейшее устройство.

Пример конечного автомата

Простой пример конечного автомата — электронны е часы. Самые обычные электронные часы являются многофункциональным прибором, который может:

показать время и дату;

прозвенеть в нужное время ;

дать возможность настроить время, дату, будильник ;

есть кнопка, нажатие которой регулирует переходы между состояниями: у становка минут, установка часов, установка даты, настройка будильника и др. ;

Пользователям логика настройки электронных часов ясна и кажется простой. Беря в руки подобное устройство, мало кто задумыва ет ся, что это на самом деле такое. А это конечный детерминированный автомат.

Заключение

Теория автоматов — это научный раздел математики, который изучает возможность реализовывать простые автоматные устройства для люде й н а основе математических моделей.

Мы будем очень благодарны

если под понравившемся материалом Вы нажмёте одну из кнопок социальных сетей и поделитесь с друзьями.

Источник

Теория автоматов

Теория автоматов — раздел дискретной математики, изучающий абстрактные автоматы — вычислительные машины, представленные в виде математических моделей — и задачи, которые они могут решать.

Теория автоматов наиболее тесно связана с теорией алгоритмов: автомат преобразует дискретную информацию по шагам в дискретные моменты времени и формирует результат по шагам заданного алгоритма.

Содержание

Терминология

Символ — любой атомарный блок данных, который может производить эффект на машину. Чаще всего символ — это буква обычного языка, но может быть, к примеру, графическим элементом диаграммы.

Говорят, что язык L читается (принимается) автоматом M, если он состоит из слов w на базе алфавита таких, что если эти слова вводятся в M, по окончанию обработки он приходит в одно из принимающих состояний F:

Обычно автомат переходит из состояния в состояние с помощью функции перехода , читая при этом один символ из ввода. Есть также автоматы, которые могут перейти в новое состояния без чтения символа. Функция перехода без чтения символа называется -переход (эпсилон-переход).

Применение

Практически теория автоматов применяется при разработке лексеров и парсеров для формальных языков (в том числе языков программирования), а также при построении компиляторов и разработке самих языков программирования.

Другое важнейшее применение теории автоматов — математически строгое нахождение разрешимости и сложности задач.

Источник

Теория автоматов, конечные автоматы

Структура, конструкция, принцип действия различных автоматов в значительной мере определяются его функциональным назначением. Различают технологические, транспортные, вычислительные, военные и другие автоматы. В различных отраслях промышленности широко внедряются целые автоматические комплексы, предназначенные для выполнения сложных технологических процессов. Разрабатываются и строятся автоматы, реализующие разнообразные логические функции (Логические машины).

Теория автоматов — раздел кибернетики, возникший под влиянием запросов техники цифровых вычислительных и управляющих машин. Дискретные автоматы, изучаемые в теории автоматов, являются абстрактными моделями реальных систем (как технических, так и биологических), которые перерабатывают дискретную (цифровую) информацию дискретными временными тактами.

В основе теории автоматов лежат точные математические понятия, формализующие интуитивные представления о функционировании (поведении) автомата и о его структуре (внутреннем устройстве).

При этом под преобразованием информации всегда понимается операция, преобразующая последовательности входные, составленные из букв входного алфавита, в последовательности выходные, составленные из букв выходного алфавита.

Широко применяется аппарат математической логики, алгебры, теории вероятностей, комбинаторики и теории графов.

Проблематика теории автоматов в некоторой своей части (структурная теория автоматов) выросла из теории релейно-контактных схем, которая начала складываться в конце 1930-х гг. с привлечением методов алгебры логики.

В структурной теории автоматов исследуются различного рода схемы, предназначаемые для описания того, как сложный автомат создается из более простых компонент (элементов), надлежащим образом соединенных в единую систему.

Другое направление, называемое абстрактной теории автоматов, изучает поведение автоматов (т. е. характер осуществляемого ими преобразования информации) при отвлечении от специфики их внутреннего устройства и возникло в 1950-х гг.

В рамках абстрактной теории автоматов содержание понятий «автомат» и «машина» исчерпывается, по существу, стандартным описанием того преобразования информации, которое осуществляется автоматом. Такое преобразование может быть детерминированным, но может иметь и вероятностную природу.

Наиболее изученными являются детерминированные машины (автоматы), к которым относятся конечные автоматы — главный объект изучения в теории автоматов.

Конечный автомат характеризуется конечностью объема памяти (числа внутренних состояний) и задается посредством функции перехода. При некоторой целесообразной идеализации все современные математические машины и даже мозг, с точки зрения их функционирования, можно рассматривать как конечные автоматы.

Термины «последовательностная машина», «автомат Мили», «автомат Мура» употребляются в литературе (причем не одинаково всеми авторами) как синонимы термина «конечный автомат» либо для подчеркивания тех или иных особенностей в функциях перехода конечного автомата.

К автоматам с неограниченной памятью относится машина Тьюринга, способная осуществлять (потенциально) любое эффективное преобразование информации. Понятие «машина Тьюринга» возникло раньше понятия «конечный автомат» и изучается преимущественно в теории алгоритмов.

Абстрактная теория автоматов тесно связана с известными алгебраическими теориями, например с теорией полугрупп. С прикладной точки зрения представляют интерес результаты, которые характеризуют преобразование информации в автомате в терминах его объема памяти.

Так, например, обстоит дело в задачах с экспериментами над автоматами (работы Э. Ф. Мура и др.), в которых по результатам экспериментов получаются те или иные сведения о функциях перехода автомата или об его объеме памяти.

Другая задача заключается в оценке периодов выходных последовательностей, исходя из имеющихся сведений об объеме памяти автомата и о периодах входных последовательностей.

Большое значение имеют разработка приемов минимизации памяти конечных автоматов и исследование их поведения в случайных средах.

В абстрактной теории автоматов проблема синтеза заключается в следующем. В терминах некоторого четко формализованного языка записываются условия, предъявляемые к поведению проектируемого автомата (к событию, представимому в автомате). При этом требуется выработать методы, которые по любому записанному условию:

1) выясняют, существует ли такой конечный автомат, что осуществляемое им преобразование информации удовлетворяет этому условию;

2) если да, то строят функции перехода такого конечного автомата или же оценивают его объем памяти.

Решение проблемы синтеза в такой постановке предполагает предварительное создание удобного языка для записи условий работы автомата с удобными алгоритмами перехода от записи к переходным функциям.

В структурной теория автоматов проблема синтеза заключается в построении из элементов заданного типа схемы, которая реализует конечный автомат, заданный своими функциями перехода. При этом обычно выдвигают некоторый критерий оптимальности (например, минимальность числа элементов) и стремятся получить оптимальную схему.

Как выяснилось впоследствии, значит, часть методов и понятий, выработанных ранее применительно к релейно-контактным схемам, применима и для схем других типов.

В связи с развитием электронной техники наибольшее распространение нашли схемы из функциональных элементов (логические сети). Частным случаем логических сетей являются абстрактные нервные сети, элементы которых называются нейронами.

Разработано много методов синтеза в зависимости от типа схем и от преобразования информации, для реализации которого они предназначены (Синтез релейных устройств).

Конечный автомат — математическая модель управляющей системы с фиксированным (не способным к увеличению в процессе работы) размером памяти.

Понятие конечный автомат является математической абстракцией, характеризующей общие черты множества управляющих систем (например, многотактного релейного устройства). У всех таких систем имеются общие признаки, которые естественно принять в качестве определения конченого автомата.

Всякий конченый автомат имеет вход, подвергающийся внешним воздействиям, и внутренние элементы. Как для входа, так и для внутренних элементов существует фиксированное число дискретных состояний, которые они способны принимать.

Изменение состояний входа и внутренних элементов происходит в дискретные моменты времени, интервалы между которыми называются тактами. Внутреннее состояние (состояние внутренних элементов) в конце такта полностью определено внутренним состоянием и состоянием входа в начале такта.

К указанной характеристике могут быть сведены все другие определения конченого автомата, в частности определения, предполагающие у конченого автомата наличие выхода, зависящего от внутреннего состояния автомата в данный момент.

С точки зрения такой характеристики, для описания конченого автомата не имеет никакого значения природа его входов и внутренних состояний. Можно вместо входов и состояний рассматривать просто их номера в произвольно выбранной нумерации.

Конечный автомат будет задан, если будет указана зависимость номера его внутреннего состояния от номера предыдущего внутреннего состояния и номера предыдущего состояния входа. Такое задание может иметь вид конечной таблицы.

Другой распространенный способ задания конченого автомата — построение т. н. диаграммы переходов. Состояния входа часто называются просто входами, а внутреннего состояния — просто состояниями.

Конечный автомат может быть моделью как технических устройств, так и некоторых биологических систем. Автоматы первого типа являются, например, релейные устройства и различные электронные вычислительные машины, в т. ч. программируемые логические контроллеры.

В случае релейного устройства роль состояний входа играют комбинации состояний воспринимающих элементов релейного устройства (каждая комбинация таких состояний представляет собой «сложное состояние», характеризуемое указанием для всех воспринимающих элементов тех дискретных состояний, которые они имеют в данный момент). Аналогично, комбинации состояний промежуточных элементов релейного устройства играют роль внутренних состояний.

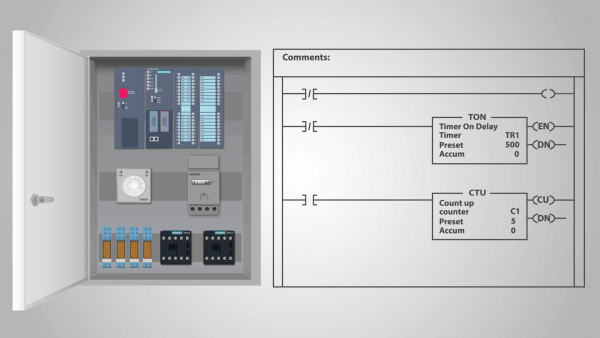
Программируемый логический контроллер (ПЛК) представляет собой пример устройства релейного действия, которое может быть названо автономным конечным автоматом.

Действительно, после того как в ПЛК введена программа и контроллер начал вычисление, она не подвергается внешним воздействиям, причем каждое ее последующее состояние полностью определено ее предыдущим состоянием. Можно считать, что вход в каждом такте имеет одно и то же состояние.

Обратно, всякий конечный автомат, имеющий единственное возможное состояние входа, естественно называть автономным, поскольку в этом случае внешняя среда не несет информации, управляющей его поведением.

Источник

Основные понятия теории автоматов

Все рассмотренные выше устройства относятся к классу комбинационных схем, то есть дискретных устройств без памяти. Наряду с ними в цифровой технике широкое распространение получили последовательностные автоматы, или, иначе, комбинационные схемы, объединенные с элементами памяти.

Под термином автомат можно понимать некоторое реально существующее устройство, функционирующее на основании как сигналов о состоянии внешней среды, так и внутренних сигналов о состоянии самого автомата. В этом плане ЭВМ может быть рассмотрена как цифровой автомат. Под цифровым автоматом понимается устройство, предназначенное для преобразования цифровой информации. С другой стороны, под термином автомат можно понимать математическую модель некоторого устройства. Общая теория автоматов подразделяется на две части: абстрактную и структурную теорию автоматов. Различие между ними состоит в том, что абстрактная теория абстрагируется от структуры как самого автомата, так и входных и выходных сигналов. В абстрактной теории анализируются переходы автомата под воздействием абстрактных входных слов и формируемые на этих переходах абстрактные выходные слова.

В структурной теории рассматривается структура как самого автомата, так и его входных и выходных сигналов, способы построения автоматов из элементарных автоматов, способы кодирования входных и выходных сигналов, состояний автомата.

В соответствии с этим принято различать две модели автоматов: структурную и абстрактную. Абстрактная модель применяется при теоретическом рассмотрении автоматов. Структурная модель служит для построения схемы автомата из логических элементов и триггеров и предназначена для выполнения функции управления.

Понятие состояние автомата используется для описания систем, выходы которых зависят не только от входных сигналов, но и от предыстории, то есть информации о том, что происходило с автоматом в предыдущий интервал времени. Состояние автомата позволяет устранить время как явную переменную и выразить выходные сигналы как функцию состояний и входных сигналов.

По виду функции выходов все множество автоматов можно подразделить на два класса: автоматы Мили и автоматы Мура.

Автоматами Мура, или автоматами первого типа, называют автоматы, для которых абстрактное выходное слово w(t) не зависит явно от входного слова z(t), а определяется только состоянием автомата в момент времени t. Закон функционирования автомата Мура может быть описан системой уравнений:

К автоматам второго типа, или автоматам Мили, относятся автоматы, поведение которых может быть описано системой уравнений:

Следовательно, в отличие от автомата Мура для автомата Мили выходной символ w(t) зависит не только от текущего состояния, но и от входного символа.

Между моделями автоматов Мили и Мура существует соответствие, позволяющее преобразовать закон функционирования одного из них в другой.

Отличие С-автомата от моделей автоматов Мили и Мура заключается в том, что он одновременно реализует две функции выходов l₁ и l₂, каждая из которых характерна для одной из двух моделей.

Источник