что такое теорема обратная теорема

Обратная теорема

Полезное

Смотреть что такое «Обратная теорема» в других словарях:

ОБРАТНАЯ ТЕОРЕМА — теорема, условием которой служит заключение исходной (прямой) теоремы, а заключением условие … Большой Энциклопедический словарь

обратная теорема — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN converse theorem … Справочник технического переводчика

обратная теорема — теорема, условием которой служит заключение исходной (прямой) теоремы, а заключением условие. * * * ОБРАТНАЯ ТЕОРЕМА ОБРАТНАЯ ТЕОРЕМА, теорема, условием которой служит заключение исходной (прямой) теоремы, а заключением условие … Энциклопедический словарь

ОБРАТНАЯ ТЕОРЕМА — теорема, условием к рой служит заключение теоремы исходной (прямой), а заключением условие. Обратной к О. т. будет исходная (прямая) теорема, так что прямая и О. т. взаимно обратны. О. т. равносильна теореме, противоположной к прямой, т. е.… … Математическая энциклопедия

ОБРАТНАЯ ТЕОРЕМА — теорема, условием к рой служит заключение исходной (прямой) теоремы, а заключением условие … Естествознание. Энциклопедический словарь

Теорема Фалеса — Эта теорема о параллельных прямых. Об угле, опирающемся на диаметр, см. другую теорему. Теорема Фалеса одна из теорем планиметрии. Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести… … Википедия

Теорема — (греч. theorema, от theoréo рассматриваю, исследую) предложение некоторой дедуктивной теории (см. Дедукция), устанавливаемое при помощи Доказательства. Каждая дедуктивная теория (математика, многие её разделы, логика, теоретическая… … Большая советская энциклопедия

Теорема Пифагора — Теорема Пифагора одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Содержание 1 … Википедия

ОБРАТНАЯ СВЯЗЬ — воздействие результатов к. л. процесса на его протекание. Если при этом интенсивность процесса возрастает, то О. с. наз. п о л о ж и т е л ь н о й, а в противопол. случае о т р и ц а т е л ь н о й. Отрицат. О. с. может обеспечить автоматич.… … Физическая энциклопедия

обратная предельная теорема — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN converse limit theorem … Справочник технического переводчика

Источник

ОБРА́ТНАЯ ТЕОРЕ́МА

Том 23. Москва, 2013, стр. 536-537

Скопировать библиографическую ссылку:

ОБРА́ТНАЯ ТЕОРЕ́МА, тео­ре­ма, ус­ло­ви­ем ко­то­рой слу­жит за­клю­че­ние ис­ход­ной (пря­мой) тео­ре­мы, а за­клю­че­ние – ус­ло­ви­ем. Об­рат­ной к О. т. яв­ля­ет­ся ис­ход­ная (пря­мая) тео­ре­ма. Т. о., пря­мая и О. т. вза­им­но об­рат­ны. Напр., тео­ре­мы «ес­ли два уг­ла тре­уголь­ни­ка рав­ны, то их бис­сек­три­сы рав­ны» и «ес­ли две бис­сек­три­сы тре­уголь­ни­ка рав­ны, то со­от­вет­ст­вую­щие им уг­лы рав­ны» яв­ля­ют­ся об­рат­ны­ми друг дру­гу. Из спра­вед­ли­во­сти к.-л. тео­ре­мы, во­об­ще го­во­ря, не сле­ду­ет спра­вед­ли­вость об­рат­ной к ней тео­ре­мы. Напр., тео­ре­ма «ес­ли чис­ло де­лит­ся на 6, то оно де­лит­ся и на 3» вер­на, а О. т. «ес­ли чис­ло де­лит­ся на 3, то оно де­лит­ся и на 6» не­вер­на. Да­же ес­ли О. т. вер­на, для её до­ка­за­тель­ст­ва мо­гут ока­зать­ся не­дос­та­точ­ны­ми сред­ства, ис­поль­зуе­мые при до­ка­за­тель­ст­ве пря­мой тео­ре­мы. Напр., в евк­ли­до­вой гео­мет­рии вер­ны как тео­ре­ма «две пря­мые, имею­щие об­щий пер­пен­ди­ку­ляр, не пе­ре­се­ка­ют­ся», так и об­рат­ная к ней тео­ре­ма «две не­пе­ре­се­каю­щие­ся пря­мые на плос­ко­сти име­ют об­щий пер­пен­ди­ку­ляр». Од­на­ко вто­рая (об­рат­ная) тео­ре­ма ос­но­вы­ва­ет­ся на евк­ли­до­вой ак­сио­ме о па­рал­лель­ных, то­гда как для до­ка­за­тель­ст­ва пер­вой эта ак­сио­ма не нуж­на. В гео­мет­рии Ло­ба­чев­ско­го вто­рая тео­ре­ма про­сто не­вер­на, то­гда как пер­вая ос­та­ёт­ся в си­ле. О. т. рав­но­силь­на тео­ре­ме, про­ти­во­по­лож­ной к пря­мой, т. е. тео­ре­ме, в ко­то­рой ус­ло­вие и за­клю­че­ние пря­мой тео­ре­мы за­ме­не­ны их от­ри­ца­ния­ми. По­это­му пря­мая тео­ре­ма рав­но­силь­на тео­ре­ме, про­ти­во­по­лож­ной к об­рат­ной, т. е. тео­ре­ме, ут­вер­ждаю­щей, что ес­ли не­вер­но за­клю­че­ние пер­вой тео­ре­мы, то не­вер­но и её ус­ло­вие. Из­вест­ный спо­соб «до­ка­за­тель­ст­ва от про­тив­но­го» как раз пред­став­ля­ет со­бой за­ме­ну до­ка­за­тель­ст­ва пря­мой тео­ре­мы до­ка­за­тель­ст­вом тео­ре­мы, про­ти­во­по­лож­ной к об­рат­ной. Спра­вед­ли­вость обе­их вза­им­но об­рат­ных тео­рем оз­на­ча­ет, что вы­пол­не­ние ус­ло­вия лю­бой из них не толь­ко дос­та­точ­но, но и не­об­хо­ди­мо для спра­вед­ли­во­сти за­клю­че­ния (см. Не­об­хо­ди­мые и дос­та­точ­ные ус­ло­вия ).

Источник

Что такое теорема обратная теорема

ТЕМА УРОКА: Обратная теорема

Обратная теорема, теорема, условием которой служит заключение исходной теоремы, а заключением — условие. Обратной к Обратная теорема будет исходная теорема. Таким образом, Обратные теоремы взаимно обратны. Например, теоремы: «если два угла треугольника равны, то их биссектрисы равны» и «если две биссектрисы треугольника равны, то соответствующие им углы равны» — являются обратными друг другу. Из справедливости какой-нибудь теоремы, вообще говоря, не следует справедливость обратной к ней теоремы. Например, теорема: «если число делится на 6, то оно делится на 3» — верна, а Обратная теорема: «если число делится на 3, то оно делится на 6» — неверна. Даже если Обратная теорема верна, для её доказательства могут оказаться недостаточными средства, используемые при доказательстве прямой теоремы. Например, в евклидовой геометрии верны как теорема «две прямые на плоскости, имеющие общий перпендикуляр, не пересекаются», так и обратная к ней теорема «две непересекающиеся прямые на плоскости имеют общий перпендикуляр». Однако вторая (обратная) теорема основывается на евклидовой аксиоме параллельных, тогда как для доказательства первой эта аксиома не нужна. В Лобачевского геометрии вторая просто неверна, тогда как первая остаётся в силе. Обратная теорема равносильна теореме, противоположной к прямой, т. е. теореме, в которой условие и заключение прямой теоремы заменены их отрицаниями. Поэтому прямая теорема равносильна теореме, противоположной к обратной, т. е. теореме, утверждающей, что если неверно заключение прямой теоремы, то неверно и её условие. Известный способ «доказательства от противного» как раз и представляет собой замену доказательства прямой теоремы доказательством теоремы, противоположной к обратной. Справедливость обеих взаимно обратных теорем означает, что выполнение условия любой из них не только достаточно, но и необходимо для справедливости заключения.

Что же такое необходимое и достаточное условие.
Необходимые и достаточные условия. Необходимыми условиями правильности утверждения называются такие условия, без соблюдения которых утверждение заведомо не может быть верным, а достаточными условиями правильности утверждения называются условия, при выполнении которых утверждение заведомо верно. Например, необходимым условием делимости целого числа на 2 является то, чтобы число, будучи записано в десятичной системе счисления, не кончалось цифрой 7. Условие это необходимо, но не достаточно, так как, например, число 23 не кончается цифрой 7 и всё-таки не делится на 2. Достаточным условием делимости числа на 2 является то, чтобы оно кончалось цифрой 0. Это условие достаточно, но не необходимо, так как число 38 не кончается цифрой 0 и все-таки делится на 2. Обычно употребляемый признак делимости на 2 (чтобы число делилось на 2, необходимо и достаточно, чтобы последняя его цифра делилась на 2) является примером условия одновременно необходимого и достаточного. Часто выражение «необходимо и достаточно» заменяется выражением «тогда и только тогда» или же выражением «в том и только в том случае».

Необходимые и достаточные условия обладают наибольшей познавательной ценностью. В сложных математических проблемах разыскание удобных для пользования необходимые и достаточные условия бывает иногда чрезвычайно трудным. В таких случаях достаточные условия стараются сделать, возможно, более широкими, т. е. охватывающими возможно большее число случаев, в которых интересующий нас факт всё ещё имеет место, а необходимые условия — возможно более узкими, т. е. охватывающими возможно меньше лишних случаев, в которых изучаемый факт уже не имеет места. Таким образом, достаточные условия постепенно сближаются с необходимыми.

Теперь немного подробней рассмотрим Лобачевского геометрию, о какой мы вспоминали выше.

Лобачевского геометрия, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на аксиому о параллельных Лобачевского. Евклидова аксиома о параллельных гласит: через точку, не лежащую на данной прямой, проходит только одна прямая, лежащая с данной прямой в одной плоскости и не пересекающая её. В Лобачевского геометрия вместо неё принимается следующая аксиома: через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её. Казалось бы, эта аксиома противоречит чрезвычайно привычным представлениям. Тем не менее как эта аксиома, так и вся Лобачевского геометрия имеет вполне реальный смысл.

Рассмотрим реальный примет обратной теоремы с доказательством.

Файл:T.gif Теорема о трех перпендикулярах.

Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и наклонной.

Файл:T.gif Обратная теореме о трех перпендикулярах.

Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна наклонной, то она перпендикулярна и её проекции.

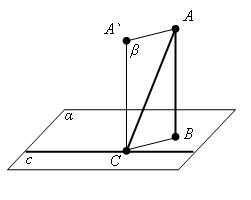
Пусть АВ – перпендикуляр к плоскости «a», АС – наклонная и «с» – прямая в плоскости «a», проходящая через основание наклонной СK. Проведем прямую СК, параллельно прямой АВ. Прямая СК перпендикулярна плоскости «a» (по этой теореме, так как она параллельна АВ), а значит и любой прямой этой плоскости, следовательно, СК перпендикулярна прямой «с». Проведем через параллельные прямые АВ и СК плоскость «b» (параллельные прямые определяют плоскость, причем только одну). Прямая «с» перпендикулярна двум прямым лежащим в плоскости «b», это АС по условию и СК по построению, значит она перпендикулярна и любой прямой, принадлежащей этой плоскости, значит перпендикулярна и прямой ВС. Другими словами проекция ВС перпендикулярна прямой «с», лежащей в плоскости «a».

Еще один вид интерпретации данной теоремы:

Файл:T.gif Теорема. Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

Аналогично теореме о трех перпендикулярах если прямая с перпендикулярна наклонной CA, то она, будучи перпендикулярна и прямой CA`, перпендикулярна плоскости β, а значит, и проекции наклонной BC. Теорема доказана.

Определения, изложенные в «Началах» Евклида, не удовлетворяют тре-бованиям современной науки. Вот некоторые из 23 определений, которыми на-чинается первая книга «Начал».

Такие определения нельзя считать логически конкретными.

Во-первых, в этих определениях употребляются такие понятия (часть, длина, ширина, грани-ца и т.д.), которые сами должны быть определены. Во-вторых, идея основных понятий (в современном смысле) у Евклида вообще отсутствует.

В-третьих, не-которые его определения туманны и непонятны, например, 4 и 7. Вообще же определения Евклида являются лишь описанием геометрических образов, и, как правило, для доказательства теорем он ими не пользовался.

Список использованных источников:

Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на Образовательном форуме, где на международном уровне собирается образовательный совет свежей мысли и действия. Создав блог, Вы не только повысите свой статус, как компетентного преподавателя, а и сделаете весомый вклад в развитие школы будущего. Гильдия Лидеров Образования открывает двери для специалистов высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.

Источник