что такое теорема фалеса
Теорема Фалеса: формулировка и пример решения задачи
В данной публикации мы рассмотрим одну из основных теорем по геометрии 8 класса – теорему Фалеса, которая получила такое название в честь греческого математика и философа Фалеса Милетского. Также разберем пример решения задачи для закрепления изложенного материала.
Формулировка теоремы
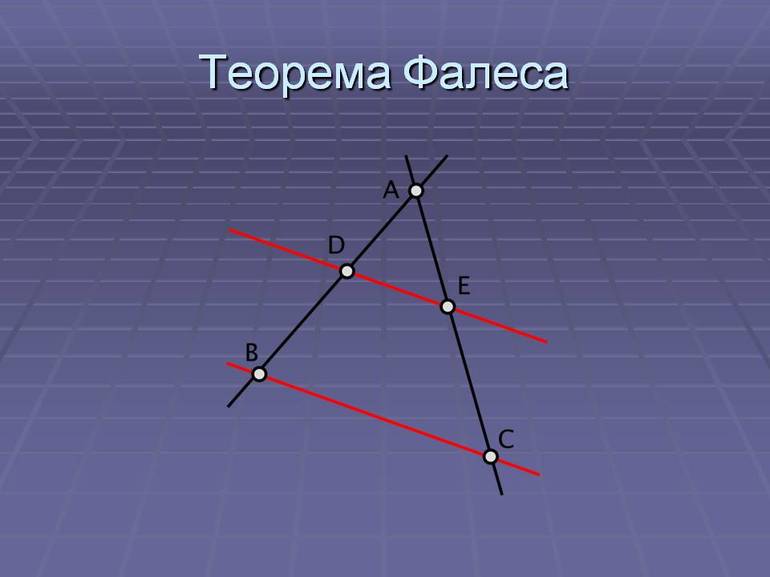
Если на одной из двух прямых отмерить равные отрезки и через их концы провести параллельные прямые, то пересекая вторую прямую они отсекут на ней равные между собой отрезки.
Примечание: Взаимное пересечение секущих не играет роли, т.е. теорема верна и для пересекающихся прямых, и для параллельных. Расположение отрезков на секущих, также, не важно.
Обобщенная формулировка
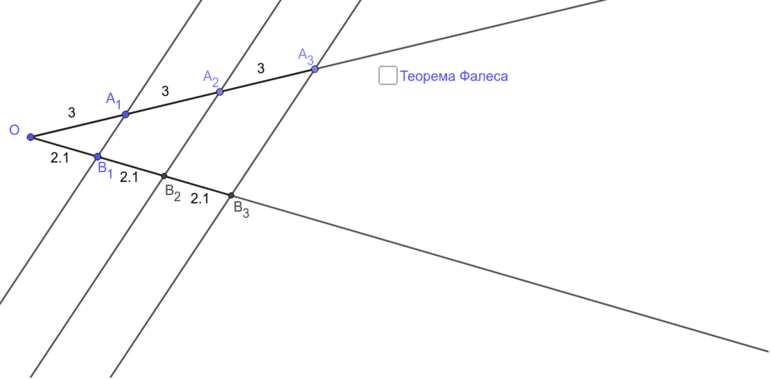
Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках*: параллельные прямые отсекают на секущих пропорциональные отрезки.
В соответствии с этим для нашего чертежа выше справедливо следующее равенство:
* т.к. равные отрезки, в т.ч., являются пропорциональными с коэффициентом пропорциональности, равным единице.
Обратная теорема Фалеса
1. Для пересекающихся секущих
Если прямые пересекают две другие прямые (параллельные или нет) и отсекают на них равные или пропорциональные отрезки, начиная от вершины, значит эти прямые являются параллельными.
Из обратной теоремы следует:
Обязательное условие: равные отрезки должны начинаться от вершины.
2. Для параллельных секущих
Отрезки на обеих секущих должны быть равны между собой. Только в этом случае теорема применима.
Пример задачи
Дан отрезок AB на плоскости. Разделите его на 3 равные части.
Решение
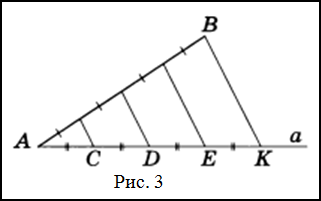
Проведем из точки A прямую a и отметим на ней три подряд идущих равных отрезка: AC, CD и DE.
Крайнюю точку E на прямой a соединяем с точкой B на отрезке. После этого через оставшиеся точки C и D параллельно BE проведем две прямые, пересекающие отрезок AB.
Образованные таким образом точки пересечения на отрезке AB делят его на три части, равные между собой (согласно теореме Фалеса).
Краткое описание
Фалес хорошо известен в истории как талантливый геометр. Именно этому человеку многие учёные приписывают открытие и доказательство многих теорем. Фалес смог разработать весьма интересный способ определения точного расстояния от берега до видимого невооружённым взглядом водного транспорта. Некоторые историки склонны полагать, что именно для этих целей учёный использовал признак некоего сходства прямоугольных треугольников. Современные последователи великого математика высоко ценят все его достижения, что он смог вывести и доказать многочисленные теоремы, законы.
Наиболее логическое доказательство правильности предположений на основании единых положений, принятых за проверенные истины, было изобретено именно греками. Сегодня историкам трудно сказать, что именно в научном перечне принадлежит Фалесу. Конечно, благодаря этому талантливому человеку Греция обрела не только философа и математика, но и естествоиспытателя.
Перед изучением теоремы обязательно нужно понять, что параллелограмм — это самый обычный четырёхугольник, у которого все противоположные стороны попарно параллельны. А вот трапеция является специфическим четырёхугольником, у которого две стороны параллельны друг другу, а две другие стороны обладают противоположными характеристиками. Изучение этой темы состоит из нескольких частей, так как первым делом нужно ознакомиться с теорией, а только потом можно приступать к решению задач.
Основные понятия
Фалесом было доказано, что две прямые линии RF и NS называются параллельными исключительно в том случае, если они проложены в одной плоскости и не пересекаются между собой вне зависимости от длины. Это правило всегда обозначают как RF || NS.
Абсолютно все существующие точки конкретной прямой располагаются на неизменном расстоянии от второй линии. А это значит, что все линии, которые параллельны одной прямой, являются параллельными между собой. Математики полагают, что итоговый угол между параллельными линиями приравнивается 0. Но это утверждение актуально только в том случае, если у отрезков одинаковые направления и они расположены под углом 180 градусов.
В качестве наглядного примера можно рассмотреть ситуацию, когда перпендикуляры RF, NS, EF относятся к одной и той же прямой РЕ и параллельны между собой. При этом прямая РЕ перпендикулярна ко всем остальным линиям. Итоговая длина сформированного отрезка перпендикуляра, расположенного между двумя параллельными прямыми, соответствует расстоянию средних линий. При изучении пространственной теоремы обязательно нужно понимать, что сразу восемь углов возникает при пересечении двух параллельных прямых третьей прямойю
Представленная специалистами формулировка теоремы Фалеса содержит много нюансов, в которых обязательно должен разбираться каждый человек, планирующий решать различные математические задачи. В противном случае будет сложно избежать самых распространённых ошибок. Даже кратко изложенная теория позволяет разобраться в главных математических тонкостях. Чтобы ученику стало понятно то, как именно нужно использовать теорему, можно задействовать специальные таблицы, которые помогут расширить итоговые математические возможности.
Научное пояснение значений
Если постараться поочерёдно отложить сразу несколько одинаковых отрезков только на одной из двух прямых линий, а потом провести прямые через конечные точки, которые смогут пересечь вторую прямую, то именно на второй прямой они смогут отсечь равные отрезки. Развёрнутая формулировка этой темы в геометрии носит название теоремы о пропорциональных геометрических отрезках. В качестве наглядного примера следует ознакомиться с этой формулой: S1S2/N1В2 = S2S3/N2N3 = S1S3/N1N3.
Важные нюансы:
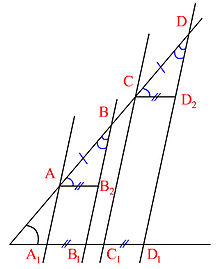
Для изучения всех нюансов этой темы необходимо рассмотреть вариант, который демонстрирует ситуацию с несвязанными парами отрезков. К примеру: существующий угол пересекает прямые LL1 || ВВ1 || СС1 || КК1 и при этом LB = СК. Через точки L и С проводят прямую линию, которая будет расположена параллельно другой стороне сформированного угла LB2В1L1 и СК2К1С1. Свойства параллелограмма тоже имеют свои особенности:
Ключевые особенности теоремы
Когда учащийся попробует на одной из двух прямых линий отложить разные отрезки, а потом через их концы провести параллельные линии, которые будут пересекать вторую прямую, то в итоге на второй прямой они обязательно отсекут идентичные между собой отрезки. Даже в школьной математике часто пользуются обобщённой теоремой Фалеса: те отрезки, которые формируются только благодаря параллельным прямым на одной линии, являются пропорциональными по отношению к другой прямой линии.
Записи с идеями Фалеса не удалось сохранить до наших дней, из-за чего историкам приходится восстанавливать информацию из разных источников. Специалистам удалось доказать, что математик из Греции вывел 7 теорем для геометрии. Основное правило гласит, что если параллельные линии, у которых пересекаются стороны угла, отсекают только на одной его стороне равные отрезки, то аналогичная ситуация происходит и на другой его стороне.
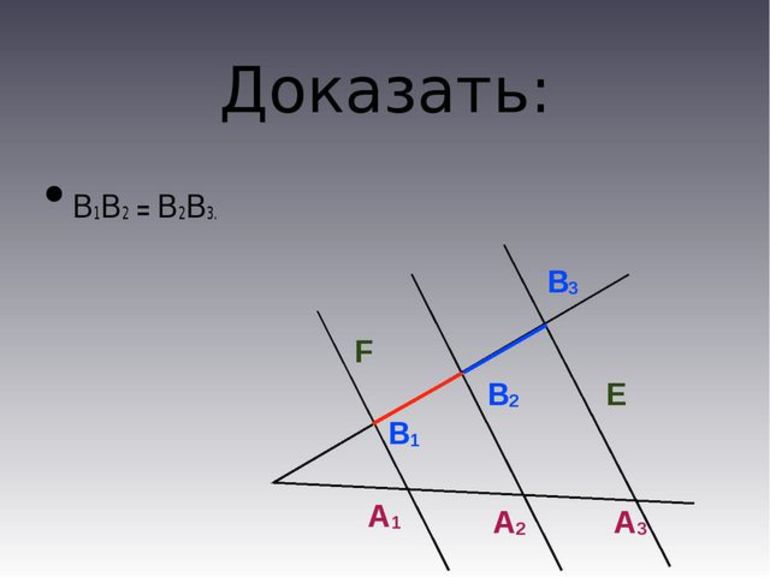
Наглядное доказательство
В качестве примера можно взять точки Н1, Н2 и Н3, которые служат для обозначения пересечения используемых параллельных отрезков только с одной стороны угла. А вот для обозначения точек пересечения этих прямых с другой стороны угла используется К1, К2 и К3. Если через точку К2 провести небольшую прямую Т1 и Т2, а также параллельную Н1 и Н2, то в итоге получится обычный параллелограмм: Н1Т1КН2 и Н2К2Т2Н3. Из этого результата можно понять, что Н1Н2 = Т1К2 и Н2Н3 = К2Т2. Этот результат был достигнут благодаря тому, что Н1Н2 = Н2Н3, а Т1К1 = К2Т2.
Теорема Фалеса
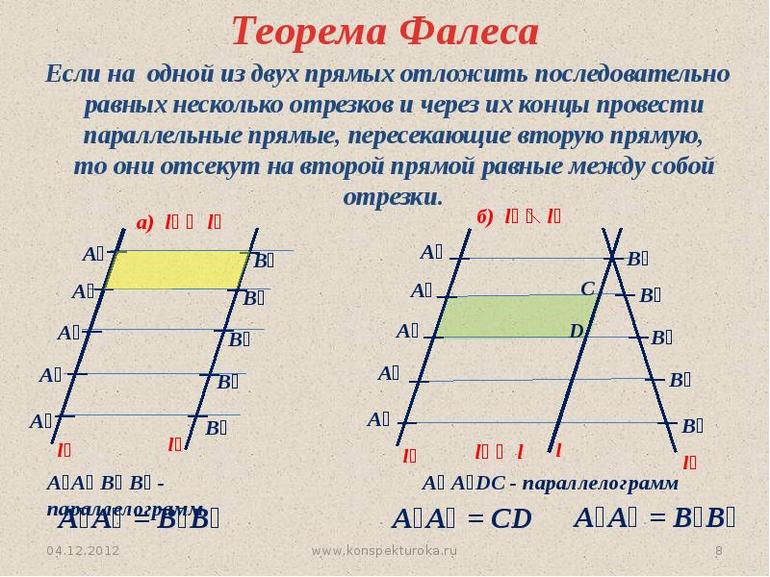
Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также неважно, где находятся отрезки на секущих.
Рассмотрим вариант с несвязанными парами отрезков: пусть угол пересекают прямые 
и при этом 
.
Проведем прямую BC. Углы ABC и BCD равны как внутренние накрест лежащие при параллельных прямых AB и CD и секущей BC, а углы ACB и CBD равны как внутренние накрест лежащие при параллельных прямых AC и BD и секущей BC. Тогда по первому признаку равенства треугольников треугольники ABC и DCB равны. Отсюда следует, что AC = BD и AB = CD. ■
Также существует обобщённая теорема Фалеса:
Параллельные прямые отсекают на секущих пропорциональные отрезки: 
Теорема Фалеса является частным случаем обобщённой теоремы Фалеса, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.
Содержание
Обратная теорема
Если в теореме Фалеса равные отрезки начинаются от вершины (часто в школьной литературе используется такая формулировка), то обратная теорема также окажется верной. Для пересекающихся секущих она формулируется так:
Если прямые, пересекающие стороны угла, отсекают на одной и на другой стороне угла равные (или пропорциональные) между собой отрезки, начиная от вершины, то такие прямые параллельны.
Таким образом (см. рис.) из того, что 
следует, что прямые 
.
Если секущие параллельны, то необходимо требовать равенство отрезков на обеих секущих между собой, иначе данное утверждение становится неверным (контрпример — трапеция, пересекаемая линией, проходящей через середины оснований).
Вариации и обобщения
Следующее утверждение, двойственно к лемме Соллертинского:
Пусть 
— проективное соответствие между точками прямой 
и прямой 
. Тогда множество прямых 
будет множеством касательных к некоторому коническому сечению (возможно, вырожденному).
В случае теоремы Фалеса коникой будет бесконечно удалённая точка, соответствующая направлению параллельных прямых.
Это утверждение, в свою очередь, является предельным случаем следующего утверждения:
Пусть — проективное преобразование коники. Тогда огибающей множества прямых будет коника (возможно, вырожденная).
Теорема Фалеса в культуре
Аргентинская музыкальная группа Les Luthiers (исп.) представила песню, посвящённую теореме. В видеоклипе для этой песни [1] приводится доказательство для прямой теоремы для пропорциональных отрезков.
Теорема Фалеса
Формулировка теоремы Фалеса
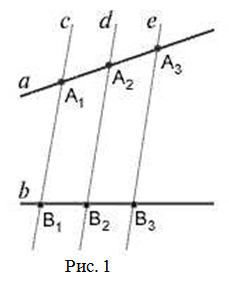
Если на одной из двух прямых отложить последовательно несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки (рис. 1).
В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также не важно, где находятся отрезки на секущих.
Обобщённая теорема Фалеса
Параллельные прямые отсекают на секущих пропорциональные отрезки (рис. 1):
Теорема Фалеса является частным случаем обобщённой теоремы Фалеса, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.
Обратная теорема Фалеса
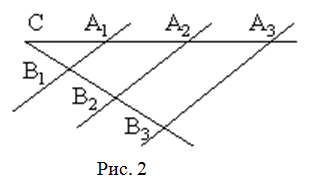
Если прямые, пересекающие две другие прямые (параллельные или нет), отсекают на обеих из них равные (или пропорциональные) между собой отрезки, начиная от вершины, то такие прямые параллельны (рис. 2).
Замечание. В обратной теореме Фалеса важно, что равные отрезки начинаются от вершины.
Примеры решения задач
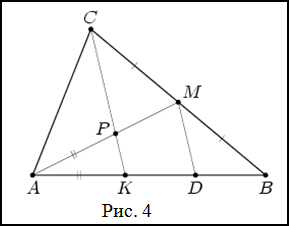
Задание. Разделить данный отрезок на четыре равные части.
Теорема Фалеса не по зубам? Тебе ответит эксперт через 10 минут!
По теореме о пропорциональных отрезках имеем, что
$$P M=K D=\frac <2>\Rightarrow B K: P M=2: 1$$
Историческая справка
Теорема Фалеса (а также теоремы Чевы и Менелая) применяются в первую очередь тогда, когда в задаче даны соотношения между отрезками. Очень часто при этом приходится проводить дополнительный отрезок.
Аргентинская музыкальная группа представила песню, посвящённую теореме. В видеоклипе для этой песни приводится доказательство для прямой теоремы для пропорциональных отрезков.
Теорема Фалеса до сих пор используется в морской навигации в качестве правила о том, что столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется курс судов друг на друга.
Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том, что вписанный угол, опирающийся на диаметр окружности, является прямым. Открытие этой теоремы действительно приписывается Фалесу, о чём есть свидетельство Прокла.