что такое темперированный строй
Хорошо темперированный
Хорошо темперированный звукоряд и чем он отличается от натурального. Почему натуральный звукоряд, просуществовавший тысячи лет, больше не применяется в современной музыке. И ещё о названии всех существующих на звукоряде октав.
Уроки музыки. Звукоряд. Часть 5.
Хорошо темперированный строй
Надеюсь, вы немного пришли в себя от потрясения вызванного информацией про энгармонизм. Могу успокоить — ты теперь знаете всё о музыкальном звукоряде, о его основной составляющей — октаве — в современной музыке состоящей из 12 равных полутонов, повторяющихся на протяжении всего звукоряда.
Осталось совсем немного пояснений, которые требуется дать и выполнить данное в начале занятия обещание. Поэтому соберитесь!
В начале занятия для нот не давались точные значения частот, зато давалось обещание всё пояснить позднее. Пришло время раскрыть этот секрет. Дело в том, что частоты, которые мы рассчитывали по обертонам эталонной струны, это частоты натурального звукоряда. И у натуральных звуков имеется особенность, которая проявила себя только на длинном звукоряде.
Именно так! На инструментах с диапазоном в пару-тройку октав такой особенности не заметно и можно было использовать расчетные данные для изготовления музыкальных инструментов. Так и поступали музыканты на протяжении всего времени, вплоть до 18 века. Тогда начали изготавливать сложные музыкальные инструменты типа орган, клавесин. И на их длинном звукоряде особенность натуральных звуков проявила себя в полной мере и потребовала принять определенные действия.
Особенность натурального звукоряда такова:
Например, ноты ля ♯ и си ♭ перестанут совпадать по высоте, а это одна и та же черная клавиша на фортепиано! Что прикажете делать? Распилить черную клавишу на части? Это не выдуманная проблема. С ней реально столкнулись музыканты и в её решении принимали участие лучшие из лучших, например, Иоган Себастьян Бах и даже китайский принц.
Решение было найдено такое: ноты в музыкальном звукоряде было решено немного подстраивать так, чтобы в октаве действительно были равные по высоте полутона. Такой звукоряд назвали темперированным.
О необходимости темперированного строя и как все происходило очень интересно рассказал Артем Варгавтик:
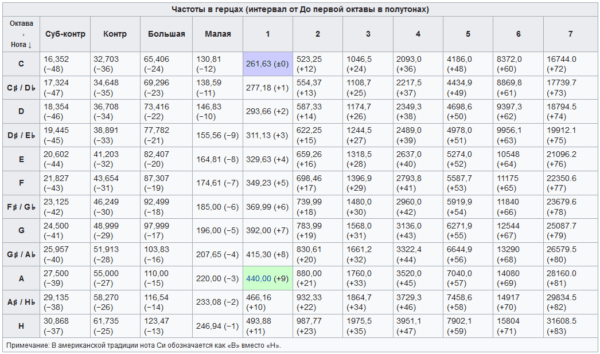
Хорошо темперированный строй и его частоты в таблице:
Частоты звуков (нот) в темперированном строе
Примечание: Если, кто-то попробует выучить все эти частоты наизусть, пусть немедленно прекратит обучение музыке и больше никогда не посещает уроки музыки от Свирельки.
Хорошо темперированный звукоряд. Названия октав
Названия октав рассмотрим на примере клавиатуры фортепиано:
Название октав на фортепиано
Самый большой звукоряд в настоящее время имеют клавишные музыкальные инструменты, такие как фортепиано. Фортепиано может озвучить 88 нот! У него 7 полных октав и еще несколько клавиш от неполных. Каждой октаве присвоено название:
Ноты называются с указанием октавы к которой они находятся, например:
Многие другие музыкальные инструменты имеют диапазон гораздо меньший чем фортепиано. Так, поперечная флейта играет в диапазоне чуть более трех октав.
Занятие про музыкальный звукоряд завершено. Если у вас остаются невыясненные вопросы и вы не полностью разобрались к какими-либо понятиями, терминами и тому подобное, напишите свои пожелания в комментариях.
При желании можете начать сначала Уроки музыки. Звукоряд. Часть 1.
И как обычно, просьба: если в статье нашли для себя что-то полезное, поделитесь с друзьями. Нам это действительно нужно и мы будем еще лучше работать для вас:
Кто желает научиться играть на каком-либо духовом инструменте, рекомендуем взять в помощь программу Свирелька:
И для особо одаренных вот запись прелюдий и фуг из цикла «Хорошо темперированный клавир» И.С.Баха:
Больше 4 часов 30 минут удовольствия. Разве что слушать частями 🙂
Хорошо темперированный
Обучающая программа Свирелька:
Научиться играть на вашем
духовом музыкальном инсрументе
поможет простая обучающая программа:
Разучите три мелодии и, если программа понравится, сможете её зарегистрировать.
Поделитесь этой страницей с друзьями
Виды строев в истории музыки
Мы все привыкли к тому, что в октаве 12 нот: 7 белых клавиш и 5 черных. И вся музыка, которую мы слышим, от классики до хард-рока создана из этих 12 нот.
А было ли так всегда? Так ли звучала музыка во времена Баха, в эпоху Средневековья или в Античности?
Условность классификации
А теперь перенесемся мысленно на несколько веков назад.
Предположим, настоятелю некоего монастыря (назовём его Доминик) пришла в голову мысль, что петь хоралы и исполнять каноны нужно везде и всегда одинаково. Но позвонить в соседний монастырь и пропеть им свою ноту «ля», чтобы они подстроили свою, он не может. Тогда всей братией они мастерят камертон, который в точности воспроизводит их ноту «ля». Доминик зовёт к себе самого музыкально одаренного послушника. Послушник с камертоном в заднем кармане подрясника садится на лошадь и два дня и две ночи, слушая свист ветра и топот копыт, скачет в соседний монастырь, чтобы унифицировать их музыкальную практику. Конечно, от скачки камертон погнулся, и дает ноту «ля» уже неточно, да и сам послушник после долгой дороги плохо помнит, так ли звучали ноты и интервалы в его родном монастыре.
В результате в двух соседних монастырях настройки музыкальных инструментов и певческих голосов оказываются разными.
Если же мы перенесемся век в VIII-IX, то обнаружим, что тогда не существовало даже нотации, то есть не было таких обозначений на бумаге, по которым любой мог бы однозначно определить, что нужно петь или играть. Нотация в ту эпоху была невменная, движение мелодии указывалось только приблизительно. Тогда, даже если бы наш незадачливый Доминик отправил в соседний монастырь целый хор на симпозиум по обмену музыкальным опытом, зафиксировать этот опыт не удалось бы, и по прошествии какого-то времени все созвучия изменились бы в ту или иную сторону.
Можно ли при такой путанице говорить о каких-либо музыкальных строях в ту эпоху? Как ни странно – можно.
Пифагоров строй
Когда люди стали использовать первые струнные музыкальные инструменты, они обнаружили интересные закономерности.
Если поделить длину струны пополам, то звук, который она издает, очень гармонично сочетается со звуком целой струны. Гораздо позже этот интервал (сочетание двух таких звуков) назвали октавой (рис.1).
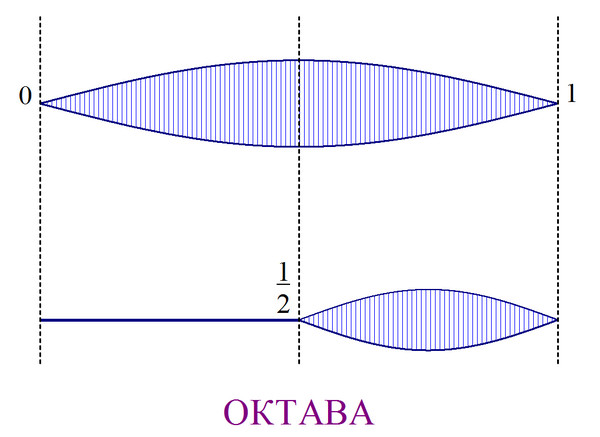
Следующим гармоничным сочетание многие считают квинту. Но, по всей видимости, в истории это было не так. Гораздо проще обнаружить другое гармоничное сочетание. Для этого нужно просто поделить струну не на 2, а на 3 части (рис.2).
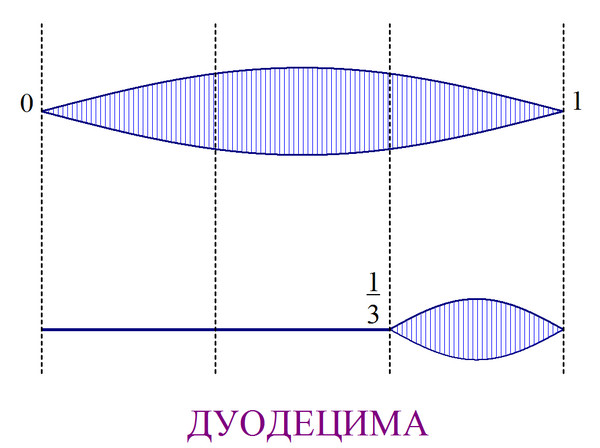
Такое соотношение сегодня известно нам как дуодецима (составной интервал).
Теперь у нас есть не просто два новых звука – октавный и дуодецимальный – теперь у нас есть два способа получать всё новые и новые звуки. Это деление на 2 и на 3.
Мы можем взять, например, дуодецимальный звук (т.е. 1/3 струны) и делить уже эту часть струны. Если поделим ее на 2 (получится 1/6 часть исходной струны), то будет звук, который на октаву выше, чем дуодецимальный. Если поделим на 3, то получим звук, дуодецимальный от дуодецимального.
Можно не только делить струну, но и идти в обратном направлении. Если длину струны увеличить в 2 раза, то получим звук на октаву ниже; если увеличить в 3 раза, то на дуодециму ниже.
Кстати, если дуодецимальный звук опустить на одну октаву, то есть. увеличить длину в 2 раза (получим 2/3 исходной длины струны), то мы получим ту самую квинту (рис.3).
Как видим, квинта – интервал, производный от октавы и дуодецимы.
Обычно первым, кто догадался использовать шаги деления на 2 и на 3 для построения нот, называют Пифагора. Так ли это на самом деле, сказать довольно трудно. И сам Пифагор – личность почти мифическая. Самые ранние письменные изложения его работ, которые нам известны, были написаны через 200 лет после его смерти. Да и вполне можно допустить, что музыканты до Пифагора использовали эти принципы, просто не формулировали (или не записывали) их. Принципы эти универсальные, диктуются законами природы, и, если музыканты ранних веков стремились к гармонии, обойти их они не могли.
Посмотрим, какие же ноты мы получим, шагая по двойкам или по тройкам.
Если делить (или умножать) длину струны на 2, то мы всегда будем получать ноту, которая на октаву выше (или ниже). Ноты, отличающиеся на октаву, называются одинаково, можно сказать, что «новых» нот мы таким образом не получим.
Совсем другая ситуация с делением на 3. Возьмем в качестве исходной ноты «до» и посмотрим, куда нас приведут шаги по тройкам.
Отложим на оси дуодециму за дуодецимой (рис.4).

О латинских названиях нот подробнее можно почитать здесь. Индекс π внизу ноты означает, что это ноты пифагорейского строя, так нам будет проще отличать их от нот других строев.
Как видим, именно в пифагорейской системе появились прообразы всех нот, которые мы используем сегодня. И не только нот.
Если мы возьмем ближайшие к «до» 5 нот (от «фа» до «ля»), мы получим так называемую пентатонику – интервальную систему, которая широко используется и по сей день. Ближайшие 7 нот (от «фа» до «си») дадут диатонику. Именно эти ноты и сейчас располагаются на белых клавишах фортепиано.
Чуть сложнее ситуация с черными клавишами. Сейчас между «до» и «ре» есть всего одна клавиша, и в зависимости от обстоятельств она называется либо до-диез, либо ре-бемоль. В пифагорейской системе до-диез и ре-бемоль были двумя разными нотами, их нельзя было разместить на одной клавише.
Натуральный строй
Что же заставило людей поменять пифагорейский строй на натуральный? Как ни странно, именно терция.
В пифагорейском строе большая терция (например, интервал до-ми) довольно диссонантна. На рис.4 мы видим, что, чтобы дойти от ноты «до» до ноты «ми», нам нужно сделать 4 дуодецимальных шага, 4 раза поделить длину струну на 3. Неудивительно, что у двух таких звуков окажется мало общего, мало созвучности, то есть консонанса.
Но совсем рядом с пифагорейской терцией есть терция натуральная, которая звучит гораздо более консонантно.
Пифагорейская терция
Натуральная терция
Певчие в хорах, когда появлялся этот интервал, рефлекторно брали более консонантную натуральную терцию.
Чтобы получить натуральную терцию на струне, нужно поделить её длину на 5, а затем понизить получившийся звук на 2 октавы, таким образом длина струны получится равной 4/5 (рис.5).
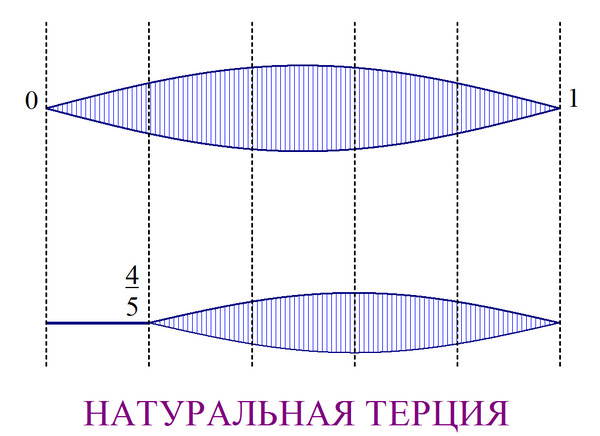
Как видим, появилось деление струны на 5 частей, которого не было в пифагорейской системе. Именно поэтому в пифагорейском строе натуральная терция невозможна.
Такая простая замена привела к пересмотру всей системы. Вслед за терцией все интервалы кроме примы, секунды, кварты и квинты изменили своё звучание. Сформировался натуральный (иногда его называют чистый) строй. Он оказался более консонантным по сравнению с пифагорейским, но дело не только в этом.
Главное, что пришло в музыку с натуральным строем – это тональность. Мажор и минор (и как аккорды, и как тональности) стали возможны только в натуральном строе. То есть формально мажорное трезвучие можно собрать и из нот пифагорейского строя, но того качества, которое позволяет организовать тональность, в пифагорейском строе у него не будет. Не случайно в античной музыке главенствующим складом была монодия. Монодия – это не просто одноголосное пение, в некотором смысле можно сказать, что это одноголосие, которое отрицает даже возможность гармонического аккомпанемента.
Объяснять значение мажора и минора музыкантам не имеет смысла.
Для не музыкантов же можно предложить следующий эксперимент. Включите любое классическое произведение от венских классиков до середины XX века. С вероятностью 95% оно будет либо в мажоре, либо в миноре. Включите современную популярную музыку. Оно будет в мажоре или миноре с вероятностью 99,9%.
Темперированный строй
Попыток темперации предпринималось великое множество. Вообще говоря, темперация – это любое отклонение интервала от чистого (натурального или пифагорейского).
Самым удачным вариантом оказалась равномерная темперация (РТС), когда октаву просто разбили на 12 «равных» интервала. «Равность» здесь понимается так: каждая следующая нота в одинаковое число раз выше предыдущей. И повысив ноту 12 раз, мы должны прийти в чистую октаву.
Решив такую задачу, мы получим 12-нотный равномерно темперированный строй (или РТС-12).
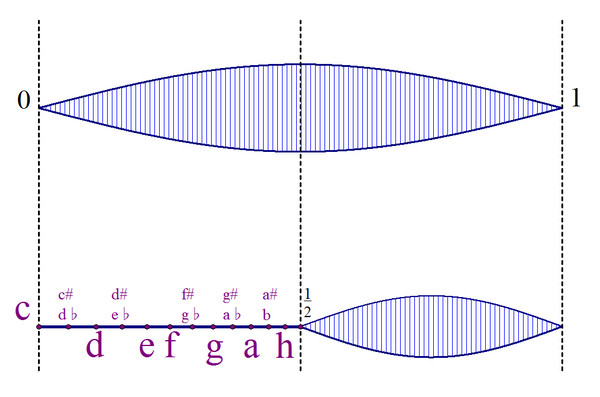
Но зачем вообще понадобилась темперация?
Дело в том, что если в натуральном строе (а именно его заменил равномерно темперированный) поменять тонику – звук от которого мы и «отсчитываем» тональность – например с ноты «до» на ноту «ре», то нарушатся все интервальные соотношения. Это ахиллесова пята всех чистых строев, и единственная возможность это исправить – это сделать все интервалы немного фальшивыми, но равными между собой. Тогда при перемещении в другую тональность по сути ничего не изменится.
Есть у темперированного строя и другие плюсы. К примеру, в нем можно исполнять музыку, как написанную для натурального строя, так и для пифагорейского.
Из минусов же самым очевидным является то, что все интервалы кроме октавы в этом строе фальшивые. Разумеется, и человеческое ухо – прибор не идеальный. Если фальшь будет микроскопической, то мы можем её просто не заметить. Но та же темперированная терция отстоит от натуральной довольно далеко.
Натуральная терция
Темперированная терция
Есть ли выходы из этой ситуации? Можно ли улучшить и этот строй?
Что дальше?
Сначала вернемся к нашему Доминику. Можем ли мы говорить, что в эпоху до звукозаписи существовали какие-то фиксированные музыкальные строи?
Наши рассуждения показывают, что даже если нота «ля» и сместится, то все построения (деления струны на 2, 3 и 5 частей) останутся теми же самыми. А значит, и системы по сути получатся одинаковыми. Разумеется, один монастырь может использовать в своей практике пифагорейскую терцию, а второй – натуральную, но, определив способ её построения, мы сможем однозначно определить музыкальный строй, а значит и возможности, которые будут в музыкальном плане у разных монастырей.
Так что же дальше? Опыт XX века показывает, что поиски не остановились на РТС-12. Как правило, создание новых строев ведется с помощью деления октавы не на 12, а на большее число частей, например, на 24 или 36. Способ этот очень механистический и малоплодотворный. Мы видели, что построения начинаются в области простого деления струны,то есть связаны с законами физики, с колебаниями этой самой струны. Лишь в самом конце построений полученные ноты заменили на удобные темперированные. Если же мы темперируем раньше, чем что-то построили в простых соотношениях, то возникает вопрос: а что же мы темперируем, от каких нот мы делаем отклонения?
Но есть и хорошие новости. Если для того, чтобы перестроить орган с ноты «до» на ноту «ре», пришлось бы подкручивать сотни труб и трубочек, то сейчас, чтобы перестроить синтезатор, достаточно нажать одну кнопку. Это значит, что вообще-то нам необязательно играть в немного фальшивых темперированных строях, мы можем использовать чистые соотношения и менять их в ту же секунду, когда возникнет такая необходимость.
А что делать, если мы хотим играть не на электронных музыкальных инструментах, а на «аналоговых»? Можно ли построить новые гармонические строи, использовать какой-то другой принцип, вместо механистического деления октавы?
Разумеется, можно, но тема эта настолько обширна, что мы вернемся к ней в другой раз.
Автор выражает благодарность композитору Ивану Сошинскому за предоставленные аудио-материалы
Равномерно темперированный строй
Равноме́рно темпери́рованный строй — музыкальный строй, при котором каждая октава делится на математически равные интервалы, чаще всего на двенадцать полутонов (
Содержание
История
12-ступенный равномерно темперированный строй возник в обстановке поисков учёными разных специальностей «идеального» строя. Исторически предшествующий натуральный строй имел ряд недостатков — прежде всего, не позволял транспонировать и модулировать в достаточно большое количество тональностей без возникновения существенных диссонансов.
Невозможно с достоверностью указать, кто именно изобрёл равномерную темперацию. Среди первых учёных, предлагавших практические способы деления октавы на 12 равных интервалов,— Генрих Грамматеус (1518) и Винченцо Галилей (1581).
Вычисление частот звуков
Можно математически вычислить частоты для всего звукоряда, пользуясь формулой:

где f0 — частота камертона (например Ля 440 Hz), а i — количество полутонов в интервале от искомого звука к эталону f0.
Последовательность вычисленных таким образом частот образует геометрическую прогрессию:
например, можно вычислить частоту звука на тон (2 полутона) ниже от камертона Ля — ноты соль: 


Частоты двух полученных нот Соль отличаются в два раза, что дает чистую октаву. Преимущества равномерной темперации также в том, что можно произвольно транспонировать пьесу на произвольный интервал вверх или вниз.
Сравнение с натуральным строем
Равномерно темперированный строй очень легко можно отобразить в виде измерения интервалов в центах
| Тон | C 1 | C# | D | Eb | E | F | F# | G | G# | A | B | H | C 2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Цент | 0 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 | 1100 | 1200 |
Следующая таблица показывает отличия интервалов равномерно-темперированного ряда с натуральным
| Интервал | Равномерно темперированные интервалы | Натуральные интервалы | Разница в центах |
|---|---|---|---|
| Прима |  |  | 0 |
| Малая секунда |  |  | −11,73 |
| Большая секунда |  |  | −3,91 |
| Малая терция |  |  | −15,64 |
| Большая терция |  |  | 13,69 |
| Кварта |  |  | 1,96 |
| Тритон |  |  | 9,78 |
| Квинта |  |  | −1,96 |
| Малая секста |  |  | −13,69 |
| Большая секста |  |  | 15,64 |
| Малая септима |  |  | 3,91 |
| Большая септима |  |  | 11,73 |
| Октава |  |  | 0 |
Расчёт конкретных высот применительно к клавиатуре фортепиано
Примечание. Значения частот рассчитаны исходя из стандартной частоты камертона ля 1 = 440 Гц.
Субконтроктава
Охватывает звуки с частотами от 16,352 Гц (включительно) до 32,703 Гц. Наименования ступеней записываются с большой буквы и справа снизу ставится цифра 2 (или два штриха). В научной нотации имеет номер 0-й
| Номер ступени | Частота, Гц | Слоговое обозначения по Гельмгольцу | Буквенное обозначение по Гельмгольцу | Американская нотация | Классическая музыкальная нотация |
|---|---|---|---|---|---|
| 1 | 16,352 | До2 | C2 | C0 | 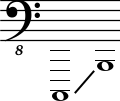 |
| 2 | 18,354 | Ре2 | D2 | D0 | |
| 3 | 20,602 | Ми2 | E2 | E0 | |
| 4 | 21,827 | Фа2 | F2 | F0 | |
| 5 | 24,500 | Соль2 | G2 | G0 | |
| 6 | 27,500 | Ля2 | A2 | A0 | |
| 7 | 30,868 | Си2 | H2 | B0 |
Контроктава
Охватывает звуки с частотами от 32,703 Гц (включительно) до 65,406 Гц. Наименования ступеней записываются с большой буквы и справа снизу ставится цифра 1 (или один штрих). В научной нотации имеет номер 1.
| Номер ступени | Частота, Гц | Слоговое обозначения по Гельмгольцу | Буквенное обозначение по Гельмгольцу | Американская нотация | Классическая музыкальная нотация |
|---|---|---|---|---|---|
| 1 | 32,703 | До1 | C1 | C1 | 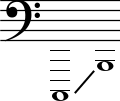 |
| 2 | 36,708 | Ре1 | D1 | D1 | |
| 3 | 41,203 | Ми1 | E1 | E1 | |
| 4 | 43,654 | Фа1 | F1 | F1 | |
| 5 | 48,999 | Соль1 | G1 | G1 | |
| 6 | 55,000 | Ля1 | A1 | A1 | |
| 7 | 61,735 | Си1 | H1 | B1 |
Большая октава
Охватывает звуки с частотами от 65,406 Гц (включительно) до 130,81 Гц. Наименования ступеней записываются с большой буквы без дополнительных цифр или штрихов. В научной нотации имеет номер 2.
| Номер ступени | Частота, Гц | Слоговое обозначения по Гельмгольцу | Буквенное обозначение по Гельмгольцу | Американская нотация | Классическая музыкальная нотация |
|---|---|---|---|---|---|
| 1 | 65,406 | До | C | C2 |  |
| 2 | 73,416 | Ре | D | D2 | |
| 3 | 82,406 | Ми | E | E2 | |
| 4 | 87,307 | Фа | F | F2 | |
| 5 | 97,999 | Соль | G | G2 | |
| 6 | 110,00 | Ля | A | A2 | |
| 7 | 123,47 | Си | H | B2 |
Малая октава
Охватывает звуки с частотами от 130,81 Гц (включительно) до 261,63 Гц. Наименования ступеней записываются с маленькой буквы без дополнительных цифр или штрихов. В научной нотации имеет номер 3.
| Номер ступени | Частота, Гц | Слоговое обозначения по Гельмгольцу | Буквенное обозначение по Гельмгольцу | Американская нотация | Классическая музыкальная нотация |
|---|---|---|---|---|---|
| 1 | 130,81 | до | c | C3 |  |
| 2 | 146,83 | ре | d | D3 | |
| 3 | 164,81 | ми | e | E3 | |
| 4 | 174,61 | фа | f | F3 | |
| 5 | 196,00 | соль | g | G3 | |
| 6 | 220,00 | ля | a | A3 | |
| 7 | 246,94 | си | h | B3 |
Первая октава
Включает звуки с частотами от 261,63 Гц (включительно) до 523,25 Гц. Наименования ступеней записываются с маленькой буквы, справа сверху пишется цифра 1 (или один штрих). В научной нотации имеет номер 4.
| Номер ступени | Частота, Гц | Слоговое обозначения по Гельмгольцу | Буквенное обозначение по Гельмгольцу | Американская нотация | Классическая музыкальная нотация |
|---|---|---|---|---|---|
| 1 | 261,63 | до 1 | c 1 | C4 | 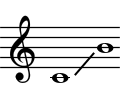 |
| 2 | 293,67 | ре 1 | d 1 | D4 | |
| 3 | 329,63 | ми1 | e 1 | E4 | |
| 4 | 349,23 | фа 1 | f 1 | F4 | |
| 5 | 392,00 | соль 1 | g 1 | G4 | |
| 6 | 440,00 | ля 1 | a 1 | A4 | |
| 7 | 493,88 | си1 | h 1 | B4 |
Вторая октава
Включает звуки с частотами от 523,25 Гц (включительно) до 1046,5 Гц. Наименования ступеней записываются с маленькой буквы, справа сверху пишется цифра 2 (или два штриха). В научной нотации имеет номер 5.
| Номер ступени | Частота, Гц | Слоговое обозначения по Гельмгольцу | Буквенное обозначение по Гельмгольцу | Американская нотация | Классическая музыкальная нотация |
|---|---|---|---|---|---|
| 1 | 523,25 | до 2 | c 2 | C5 |  |
| 2 | 587,33 | ре 2 | d 2 | D5 | |
| 3 | 659,26 | ми2 | e 2 | E5 | |
| 4 | 698,46 | фа 2 | f 2 | F5 | |
| 5 | 783,99 | соль 2 | g 2 | G5 | |
| 6 | 880,00 | ля 2 | a 2 | A5 | |
| 7 | 987,77 | си2 | h 2 | B5 |
Третья октава
Включает звуки с частотами от 1046,5 Гц (включительно) до 2093,0 Гц. Наименования ступеней записываются с маленькой буквы, справа сверху пишется цифра 3 (или три штриха). В научной нотации имеет номер 6.
| Номер ступени | Частота, Гц | Слоговое обозначения по Гельмгольцу | Буквенное обозначение по Гельмгольцу | Американская нотация | Классическая музыкальная нотация |
|---|---|---|---|---|---|
| 1 | 1046,5 | до 3 | c 3 | C6 |  |
| 2 | 1174,7 | ре 3 | d 3 | D6 | |
| 3 | 1318,5 | ми3 | e 3 | E6 | |
| 4 | 1396,9 | фа 3 | f 3 | F6 | |
| 5 | 1568,0 | соль 3 | g 3 | G6 | |
| 6 | 1760,0 | ля 3 | a 3 | A6 | |
| 7 | 1975,5 | си3 | h 3 | B6 |
Четвертая октава
Включает звуки с частотами от 2093,0 Гц (включительно) до 4186,0 Гц. Наименования ступеней записываются с маленькой буквы, справа сверху пишется цифра 4 (или четыре штриха). В научной нотации имеет номер 7.
| Номер ступени | Частота, Гц | Слоговое обозначения по Гельмгольцу | Буквенное обозначение по Гельмгольцу | Американская нотация | Классическая музыкальная нотация |
|---|---|---|---|---|---|
| 1 | 2093,0 | до 4 | c 4 | C7 |  |
| 2 | 2349,3 | ре 4 | d 4 | D7 | |
| 3 | 2637,0 | ми4 | e 4 | E7 | |
| 4 | 2793,8 | фа 4 | f 4 | F7 | |
| 5 | 3136,0 | соль 4 | g 4 | G7 | |
| 6 | 3520,0 | ля 4 | a 4 | A7 | |
| 7 | 3951,1 | си4 | h 4 | B7 |
Пятая октава
Включает звуки с частотами от 4186,0 Гц (включительно) до 8372,0 Гц. В нотации Гельмгольца наименования ступеней записываются с маленькой буквы, справа сверху пишется цифра 5 (или пять штрихов). В научной нотации имеет номер 8.
| Номер ступени | Частота, Гц | Слоговое обозначения по Гельмгольцу | Буквенное обозначение по Гельмгольцу | Американская нотация | Классическая музыкальная нотация |
|---|---|---|---|---|---|
| 1 | 4186,0 | до 5 | c 5 | C8 |  |
| 2 | 4698,6 | ре 5 | d 5 | D8 | |
| 3 | 5274,0 | ми5 | e 5 | E8 | |
| 4 | 5587,7 | фа 5 | f 5 | F8 | |
| 5 | 6271,9 | соль 5 | g 5 | G8 | |
| 6 | 7040,0 | ля 5 | a 5 | A8 | |
| 7 | 7902,1 | си5 | h 5 | B8 |
Другие равномерные темперации
Равномерно темперированный строй и другие строи
Наряду с господствующим равномерно темперированным строем в Европе существовали и существуют другие строи. Русский исследователь музыки XIX века Владимир Одоевский, например, написал так:
Широкомасштабное движение музыкантов-аутентистов практикует воспроизведение музыки прошлого в тех строях, в которых исполняемая ими музыка была написана.
См. также
Примечания
. Иосип Славенски написал произведение для электронных инструментов с названием «Музыка в Натуральной тональной системе» (1937). В нём две части, первая написана для фисгармонии Бозанкета с 53 тонами в октаве. »
(«…JOSIP STOLCER SLAVENSKI composed a composition for electronic insruments with the title Music in the Natural Tonal System (1937). It includes two movements: the first movement is written for the Bosanquet enharmonium with 53 tones in an octave»)