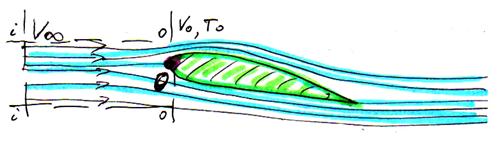
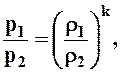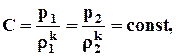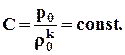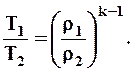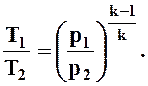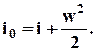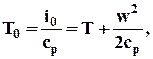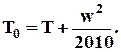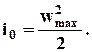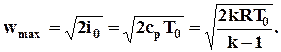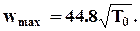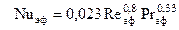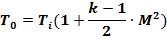что такое температура торможения при движении газа
Температура торможения
Связь параметров состояния идеального газа в адиабатном процессе
В курсе физики рассматривались следующие характерные процессы перехода газа из одного состояния в другое:
изобарный— при постоянном давлении;
В газовой динамике часто приходится рассматривать быстропротекающие процессы, при которых не успевает осуществиться теплообмен с окружающей средой. Поэтому для нее особо важное значение приобретают именно адиабатные процессы.
В этом случае давление и плотность в двух сечениях потока связаны соотношением
Отсюда следует, что для полностью заторможенного потока (скорость газа равна нулю) также выполняется условие
С учетом уравнения состояния идеального газа несложно вычислить отношения температур в адиабатном процессе.
Это дает возможность получить соотношение температур и давлений в процессе
Для полностью заторможенного потока газа энтальпия достигает максимального значения в соответствии с выражением
Температура, соответствующая этому значению энтальпии, называется температурой торможения и определяется из выражения
Для воздуха, с учетом численного значения его теплоемкости при постоянном давлении (сp = 1005 Дж/(кг·К)), температура торможения определится как
При уменьшении скорости потока газа до нуля газ приобретает температуру торможения независимо от того, каким путем и с какими потерями произошло это торможение. На практике при скоростях потока до 100м/с превышение температуры торможения по отношению к температуре в потоке составляет не более 5 0 С, что практически можно не учитывать. Однако при околозвуковых и сверхзвуковых скоростях разогрев газа за счет торможения становится весьма ощутимым и даже опасным. Так, при скорости 1000м/c рост температуры составляет уже около 500К, что во многих случаях недопустимо для тех или иных устройств («тепловой барьер» в авиации и др.).
Если применить первый закон термодинамики для энергетически изолированного процесса истечения газа и представить полное преобразование энтальпии газа в кинетическую энергию, то для максимальной скорости истечения получим
Отсюда следует выражение для максимальной скорости истечения газа
Для воздуха это выражение, с учетом численных значений R и k, приобретает вид
Следовательно, при нормальных условиях (T = 273K) максимальная скорость истечения воздуха составит всего лишь 740м/c. Очевидно, что высокие скорости истечения можно получить лишь при высоких начальных температурах газа.
Полным давлением называют давление, полученное в процессе адиабатического торможения газа до нулевой скорости, т.е.
.
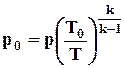
Необходимо отметить, что истинное давление, которое получается при торможении струи газа, может существенно отличаться от полного давления, определенного по приведенной формуле. Объясняется это потерями при торможении. Действительное давление в заторможенной струе газа ниже полного давления набегающей струи.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Температура торможения и давление торможения
Это уравнение относится к точке потока, где скорость равна нулю, точке теплоизоляции (но не обязательно изэнтропии), где скорость и температура равны 0. Температуры T0 и T существенно отличаются только в случае большого влияния кинетической энергии. Это достигается путем выражения температуры тормоза в числе Маха. Формула (17. 20) разделите левую сторону на C2, а правую-на величину, равную C2(17. 13) от、 7р (17.33） (17.34)） С2 2С РМТ(Т гр. Кошка- Что касается идеального газа из термодинамики、 СРЛ / t_ в _ к н » д. (17. 33)
Уравнение (17) и вместе с уравнением состояния идеального газа 〜^ = — получается V t t t (17.36)） Формула^и тормозное давление равно (17.37) ial ^ RaV5enie (17 * ^ 7) неудобно. Удобно развернуть правую сторону бинома (17. 38) однако следует помнить, что даже в несжимаемых жидкостях такие устройства, как трубки Пито, демонстрируют давление выше истинного или статического. Следовательно, формула(17. 38) учитывает как эффект сжимаемости, так и эффект, который обычно наблюдается при малых скоростях. Эффект степени сжатия заключается в следующем(17. 38).Пишет для несжимаемого тока Заполняя жидкость: 1 e » 2_ * M2. (17.39)Р 2 2. Эта формула является формулой 17.
Используя формулу (17. 4) он получается интегрированием (^2-0)с постоянной плотностью p. величина p0 — p равна Ch. 12 динамическое давление, Р0-тормозное давление потока несжимаемой жидкости. Эффект сжимаемости зависит от формулы (17. 38) (17. 39) путем деления. ^ = 1 + 1М * + ^ м + … П9-P424 (17. Сорок） Если число Маха меньше 0,2, то эффект сжимаемости не ощущается.
В случае равного энтропийного потока (например, потока в сопле) и температура тормоза, и давление тормоза остаются постоянными, даже если фактические температура и давление change. In изолированная подача, когда трение, температура тормоза постоянн, но давление тормоза уменьшает вниз по потоку. Формула тормозного давления применяется только к дозвуковым потокам. Когда датчик давления вставляется в сверхзвуковой поток, в нем или перед ним образуется скачок, поток уже не равен энтропии, и уравнение(17.(17. 38) дает завышенное значение тормозного давления. Приведем следующий пример, иллюстрирующий применение принципа вычисления изоэнтропийного потока.
На выходе сопла°Д0 TH достигается более высокое Д и не увеличивается по сравнению с изделием (а). Выберите Скорость, Массо-дисперсность выходного сечения таким образом, чтобы сопло с скачком давления возникло до скачка давления px — = 4 атм при выходном давлении= 8 атм(рис. 17. 5 и 17. 7). Во-первых, формула(17. 17) найдите условия непосредственно перед прыжком. 2•1.4-8310-1670_ ч / ° 4Л ’ 28 В1. 0 ^ 29 1. \ Г / Г „1 = 880 м / с.
Сможете применить снова. Когда вы интегрируете… 2 2 * Па _ 3″(a-1) 02 2-1. 4-6. 34-1. 033-9. 8-10 * H l / 8 ° ’2M1 ——— 045252——— 11″（631）] + 633 Выход= 447 м / с Д Мы также знаем, что T3 = 1570 * K,= 1,81 кг / м2 и= 1,24 или 2> s = 56,6 мм. Для управления расчетом используется формула(17. 20) от and3 можно определить.
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Что такое температура торможения при движении газа
Запишем сумму дифференциальных операторов в правой части уравнения
(2.4.1)
(2.4.2)
имеет размерность энтальпии и, очевидно, является некоторой специфической характеристикой энергетического состояния потока.
Для газов в довольно широком интервале температур удельную теплоемкость можно считать постоянной и
(2.4.3)
Физический смысл этой величины может быть выяснен из следующих соображений. Полная энергия потока складывается из его энтальпии и кинетической энергии, т. е. равна i*. При изоэнтропическом торможении полная энергия потока не изменяется, т. е.
(2.4.4)
В связи с этим величина i называется энтальпией торможения, а величина Т* — температурой торможения. Эти величины играют важную роль при исследовании теплообмена в потоках, двигающихся с большими скоростями.
ОСОБЕННОСТИ ТЕПЛООБМЕНА ПРИ ДВИЖЕНИИ ГАЗА
С БОЛЬШОЙ СКОРОСТЬЮ
При движении газового потока с большой скоростью процессы теплообмена значительно усложняются. Это связано с тем, что в пограничном слое благодаря силам вязкости происходит резкое уменьшение скорости от максимального её значения во внешнем потоке до нуля на поверхности тела. Большие градиенты скорости поперёк пограничного слоя приводят к возникновению значительных сил трения, работа которых переходит в теплоту. В этих условиях пограничный слой можно рассматривать как малую пространственную область, в которой происходит разогрев газа за счёт диссипации кинетический энергии. Увеличение температуры газа приводит к соответствующему изменению тепловых потоков. Кроме того, большие диапазоны изменения температуры газа в пограничном слое приводят к значительным изменениям плотности, вязкости, теплопроводности и теплоёмкости теплоносителя, что также оказывает заметное влияние на интенсивность теплообмена.
Температура восстановления. Рассмотрим движение газового потока с большой скоростью вдоль пластины (рис. 2.8). Примем, что с противоположной стороны пластина теплоизолирована. Тогда на установившемся режиме ее температура станет равной температуре непосредственно прилегающих к ней слоев газа, а теплообмен между пластиной и обтекающим ее потоком будет отсутствовать.
 |  |
| Рис. 2.8 | Рис. 2.9 |
Из-за торможения потока в пограничном слое температура газа в нем увеличивается и превышает температуру внешнего потока, увеличиваясь по мере приближения к пластине (рис. 2.8б).
Температурой восстановления Тr называется температура, которую принимает теплоизолированная (с одной стороны)пластина при обтекании её газом.
Такую же температуру будут иметь и частицы газа, непосредственно прилегающие к пластине (стенке).
Хотя частицы, прилагающие к стенке, полностью заторможены, температура восстановления оказывается несколько отличной от полной температуры набегающего газового потока. Это связано с тем, что температура восстановления зависит от двух параллельно протекающих процессов: выделения теплоты, вызванного торможением потока из-за наличия трения, и отвода теплоты в поток путём теплопроводности, возникающего из-за больших градиентов температуры по нормали к стенке в пограничном слое.
Температура восстановления определяется по формуле
,
Коэффициент восстановления зависит главным образом от режима течения в пограничном слое и числа Прандтля. Для продольно обтекаемой пластины при ламинарном пограничном слое r хорошо аппроксимируется формулой
, а при турбулентном пограничном слое формулой 
.
Так как у газов Рr о С) значениях статической температуры теплоносителя. Этим вызывается необходимость тепловой защиты поверхностей летательных аппаратов, предназначенных для больших сверхзвуковых и гиперзвуковых скоростей полета.
Важно подчеркнуть, что при теплообмене между телом и высокоскоростным потоком газа последний может отдавать теплоту стенке даже в условиях, когда температура стенки Тст превосходит статическую температуру обтекающего её потока Тт.
Плотность теплового потока. Величина и направление теплового потока между газом и стенкой определяется не соотношением между статической температурой теплоносителя Тти температурой стенки Тст, как это имеет место при малых скоростях потока, а соотношением между температурой восстановления Тr и Тст.
Соответственно формула Ньютона для этого случая должна быть записана в виде 
.
При обтекании газом теплоизолированной стенки температура её поверхности равна температуре восстановления 
, которая близка к температуре заторможенного потока и определяется по следующей формуле:
В приближенных расчетах можно считать, что 
, и тогда
.
Критериальные уравнения. Подобие процессов теплообмена при больших скоростях движения газа кроме критериев Re и Pr определяется также числом Маха, точнее комплексом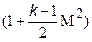 
, который обеспечивает подобие температурных полей в пограничном слое (напомним, что 
= 
) и учитывает изменение физических свойств теплоносителя, вызванных резким увеличением температуры. В этих условиях критериальное уравнение имеет вид Nu = f(Re, Pr, М).
Однако в практических расчётах для определения коэффициента теплоотдачи a при больших скоростях движения теплоносителя часто используется упрощённое критериальное уравнение типа
полученное для малых скоростей, но используемое при условии, что физические параметры газа (теплоёмкость, вязкость, теплопроводность) определяются по некоторой эффективной температуре. Значение этой температуры Тэф определяется в приближенных расчетах по формуле
или по еще более простой формуле, т.е. 
.
Исследования показали также, что для расчета местных коэффициентов теплоотдачи при движении газа с большой скоростью в каналах переменного сечения при турбулентном течении следует для каждого сечения канала использовать следующее критериальное уравнение,
но с определением критериев подобия по эффективной температуре.
2.8. КОНВЕКТИВНЫЙ ТЕПЛООБМЕН ПРИ СВОБОДНОМ
Условия возникновения свободного движения теплоносителя. Свободным называется движение теплоносителя, возникающее вследствие различия плотностей неодинаково нагретых его объёмов. Различие плотностей приводит к неоднородному полю массовых сил (например, сил тяготения), т.е. к появлению неуравновешенных сил, действующих на частицы жидкости (газа), что обусловливает возникновение архимедовой подъемной (выталкивающей) силы, которая и вызывает свободное движение теплоносителя.
Таким образом, для возникновения свободного движения необходимо:
а) наличие массовых сил (сил тяготения, центробежных сил и др.);
б) наличие неравномерного распределения плотности теплоносителя в объеме, что имеет место при неравномерном прогреве этого объема.
Температура торможения потока
Зависимость физических параметров потока от скорости его движения
Рис 3.1.2 Схема вывода уравнения полного торможения
На передней кромке обтекаемых тел всегда имеется область или точка, в которой газ полностью тормозится и скорость обтекания становится равной “0” (V=0). Эту область или точку называют критической. Если проанализировать уравнение Бернулли, то можно увидеть, что:
,
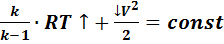
Отсюда следует, что при торможении потока его температура увеличивается и максимальное значение температуры будет соответствовать сорости V=0 (т.е. в точке торможения).
Согласно уравнения Д. Бернулли, температуру торможения потока можно опреде-лить по формуле:
, отсюда при V0=0, получим
,
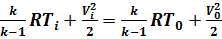
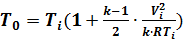
или учитывая выражение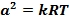 
,получим новое выражение
Из этого выражения следует, что температура торможения увеличивается с ростом числа (М), это объясняется тем, что при адиабатическом торможении кинетическая энер-гия потока преобразуется во внутреннюю энергию газа и идет на увеличение его темпе-ратуры. Это явление называется кинетическим нагревом.
Зависимость температуры торможения от чисел М
| M |
 |
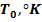Если бы не было теплопередачи, то температура газа в критических точках профи-лей обтекаемых тел была бы равна температуре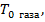 
а так она излучается в среду и рас-сеивается, отражается от поверхности тела и отводится во-внутрь тела, то температура в точке торможения будет значительно меньше температуры торможения.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет