что такое тангенциальная скорость
Общие сведения
Первая лекция для студентов, изучающих кинематику, начинается с рассмотрения тангенциального ускорения, характеризуемого произвольным движением. По сути, рассматривается неравномерное прямолинейное движение общего вида. Кинематика входит в механику и изучает перемещение объектов без учёта сил, вызвавших их движение. Под перемещением понимают изменение положения в пространстве по отношению к другому физическому телу, которое и считается точкой отсчёта. Если изменение положения связать с координатами и временем, то образуется система отсчёта. С её помощью можно определить положение объекта в любой момент.
В кинематике любые процессы принято рассматривать, приняв тело за материальную точку. То есть его размерами и формой пренебрегают. При изменении за какой-то промежуток времени точка проходит путь, описывающийся линией — траекторией. Она является скалярной величиной, а само перемещение — векторной. Движение материальной точки может происходить с разной скоростью и ускорением. Быстроту движения разделяют на среднюю и мгновенную. Вторая определяется как предел, к которому стремится скорость на бесконечно малом временном интервале: v = Δs / Δt (Δt → 0).
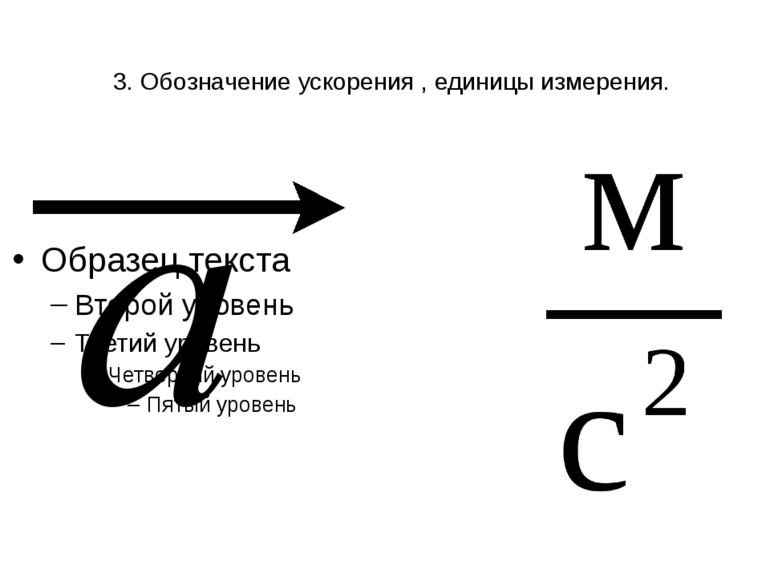
Перемещение может происходить с ускорением. Это физическая величина, определяющая изменение быстроты перемещения. Иными словами, показывает изменение положения за единицу времени. Измеряется она в метрах на секунду в квадрате. В кинематике существует три вида ускорения:
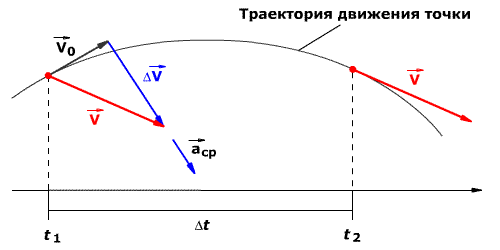
Но также используется понятие «вектор среднего ускорения тела». Определяется он как приращение вектора скорости за промежуток времени: aср = Δv / Δt. При этом он будет совпадать по направлению с вектором скорости, то есть направлен в сторону вогнутости траектории.
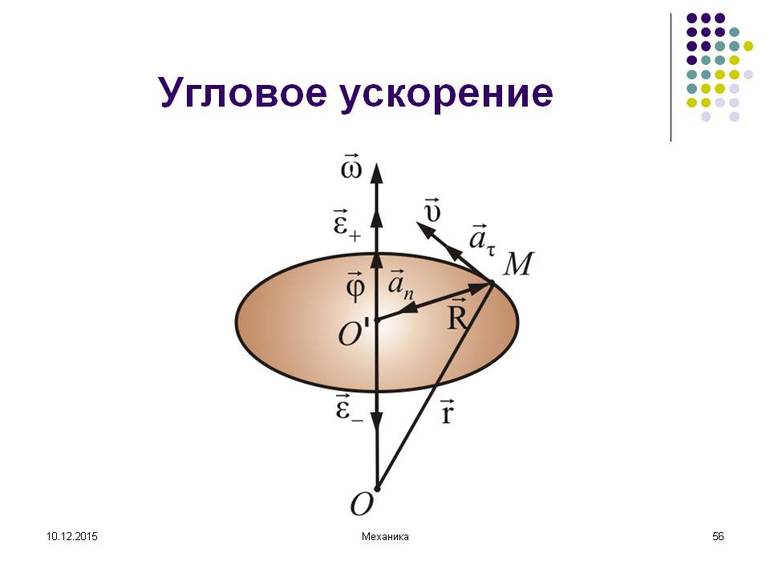
Угловое ускорение
Если имеется какая-то точка, находящаяся на вращающемся теле, то скорость её направлена по касательной. Когда движение равномерное, то линейная скорость связана с угловой равенством: v = w * r. А вот ускорение тела будет направлено по радиусу к центру окружности, причём модуль вычисляется как a = v / r либо если это точка на вращающемся теле: a = w2 * r.
В момент, когда тело поворачивается за небольшой промежуток времени на угол дельта фи, угловую скорость можно связать с условием поворота через формулу: w = Δ φ / Δ t. Если тело вращается равномерно, то промежуток времени может быть любым. В ином случае эта величина будет равна мгновенной угловой скорости.
Можно представить, что материальная точка движется неравномерно, то есть изменяется угловая скорость тела. Линейная скорость не будет представлять собой постоянную величину, в отличие от равномерного перемещения. Угол поворота равняется: w = v / r. Так как скорость не может быть константой, то отсюда следует, что и угловая скорость не будет постоянной величиной. Её изменение обозначают Δw. Она равняется разности конечной угловой скорости и начальной: Δw = wк — wн.
Изменение угловой скорости можно разделить на промежуток времени, за который оно поменяло значение: (wк — wн) / Δt. По сути, получается ускорение. Обозначается характеристика буквой эпсилон E и называется угловым ускорением. Измеряется характеристика в радианах на секунду в квадрате. Её смысл заключается в описании физической величины через отношение изменения угловой скорости тела за небольшой промежуток времени к длительности этого промежутка.
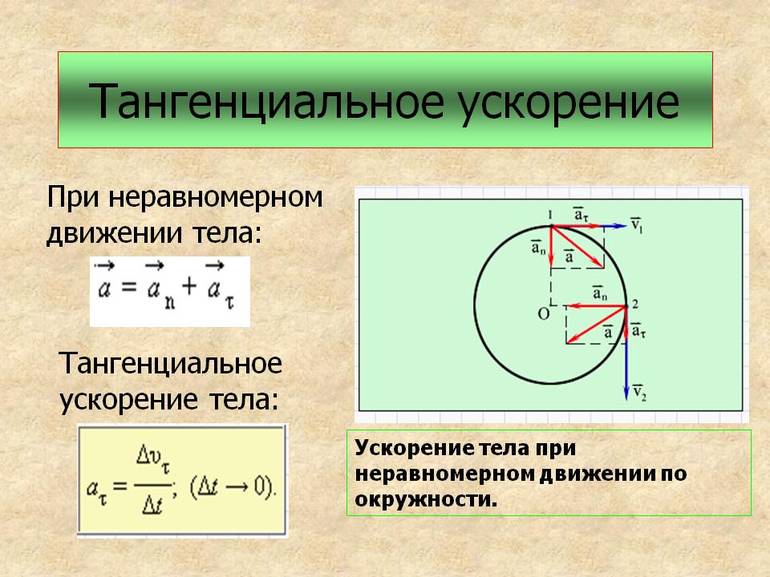
Пусть есть дуга окружности с центром. В начальный момент времени у тела есть скорость, направленная по касательной к траектории v0. Через некоторое время точка переместится по окружности на небольшое расстояние. Так как движение неравномерное, модуль скорости изменится v ≠ v0. Для того чтобы найти ускорение тела, нужно воспользоваться следующей формулой: a = Δv / Δt, при этом Δv = v — v0.
Чтобы найти эту разность, нужно воспользоваться правилом треугольника. Для этого следует перенести вектор V0 к V и соединить их линией. Радиус от центра к материальной точке можно обозначить R. Дельта V можно представить, как сумму взаимно перпендикулярных векторов. Один из них будет направленных тангенциально к радиусу, в физике обозначают его Δ Vτ, а другой радиально Δ Vr. В итоге: ΔV = Δ Vτ + Δ Vr.
Вывод формулы
Для доказательства формулы необходимо рассмотреть плоскую систему координат, в которой материальная точка изменяет своё положение по криволинейной траектории. В начальный момент её скорость будет равняться V0. Через некоторое время она изменится и станет V. На графике в плоском измерении это можно представить в виде синусоиды. В определённый момент времени скорость превышает начальную: V > V0. На схеме вектор нулевой скорости направлен из точки t0 вверх по касательной, а вектор V с нижней точки синусоиды параллельно оси ординаты.
Исходя из графика, можно сделать два вывода:
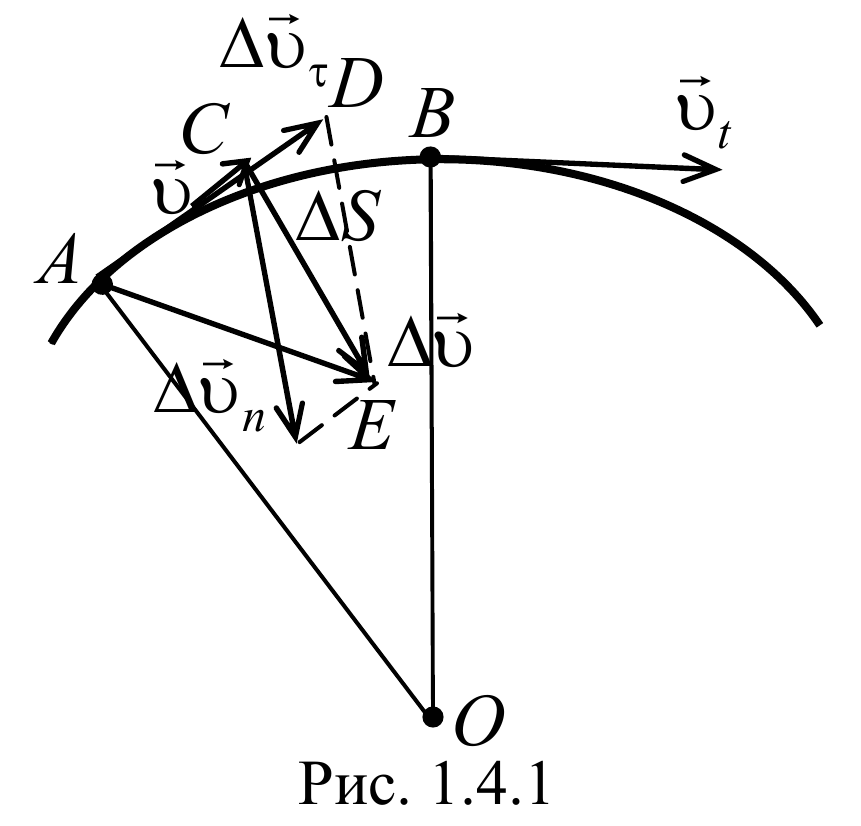
Для того чтобы построить вектор изменения Δv, нужно из конечной точки отрезка V0 провести линию к рассматриваемой точки, характеризующейся во времени скоростью V. Вершины полученного треугольника можно обозначить буквами ABD. Из верхнего угла B на сторону AD можно опустить медиану. Точка пересечения со стороной пусть будет C. Получается, что вектор Δv можно разложить на две составляющие — отрезки BC и СD. Причём медиана равняется Δvn, а изменение по оси ординаты Δvt.
Для разложения необходимо использовать вектор АС, длина которого совпадает с Vo по модулю: |AC| = |AB| = V0. Так как Δvn — результирующий вектор, то его можно вычислить через сумму: Δv = Δvn + Δvt. Причём первый член в равенстве характеризует изменение быстроты за промежуток времени по направлению, а второй — по модулю. Исходя из того, что t не равняется нулю, на него можно разделить левую и правую часть равенства: Δv / Δt = Δvn / Δt + Δvt / Δt. Если дельта-времени стремится к нулю, то формулу можно переписать в виде: lim Δv / Δt = lim Δvn / Δt + lim Δvt / Δt.
Учитывая связь между ускорениями и то, что полное значение состоит из суммы изменения быстроты движения по модулю и направлению, можно утверждать о верности формулы: a = at + an. Так как направление векторов ускорения и скорости всегда совпадают, то последний можно представить, как параметр, состоящий из двух взаимно перпендикулярных компонент:
Решение простых примеров
В школьном курсе на уроках физики учащимся для закрепления материала предлагается решить определённый тип задач, используя определение тангенциального ускорения. Это типовые примеры, объясняющие суть характеристики и её применение в реальной практике. Вот некоторые из них.
Но не всегда решаемые задания можно решить, обойдясь одной формулой. При этом значения тех или иных величин могут быть довольно сложными для проведения вычислений. В таких случаях есть резон использовать так называемые онлайн-калькуляторы. Это специализированные сайты, выполняющие подсчёт в автоматическом режиме. Из таких сервисов можно выделить: сalc, widgety, webmath. Указанные интернет-решители работают на русском языке, так что вопросов, как с их помощью выполнять расчёты, возникнуть не должно.
Сложная задача
Пусть имеется физическое тело, которое движется, замедляясь по окружности радиусом R так, что в каждый момент времени её тангенциальное и нормальное убыстрение равны друг другу по модулю. Необходимо найти зависимость скорости и полного ускорения от времени и пройденного пути. В начальный момент скорость равняется V0.
Согласно условию, тангенциальное ускорение будет отрицательным, так как точка движется, замедляясь. Для понимания задачи можно изобразить схему движения. Для этого необходимо нарисовать окружность и указать на ней вектор начальной скорости, тангенциального и нормального ускорения. Изобразить вектор полного ускорения как сумму векторов.
Подставив пределы, можно получить равенство: (1 / V) — (1 / V0) = t / R. Из полученной формулы следует выразить скорость: V = (V0 * R) / (R + V0 * t). Поделив числитель и знаменатель на радиус, ответ примет вид: V (t) = V0 / (1 + (V0 * t / R)).
Лекция №2. Элементы кинематики
1.4. Нормальное и тангенциальное ускорения при криволинейном движении
В общем случае при движении тела его скорость изменяется как по величине, так и по направлению. Для характеристики быстроты изменения скорости движения вводится понятие ускорения.
Таким образом, ускорение есть векторная величина, равная первой производной скорости по времени.
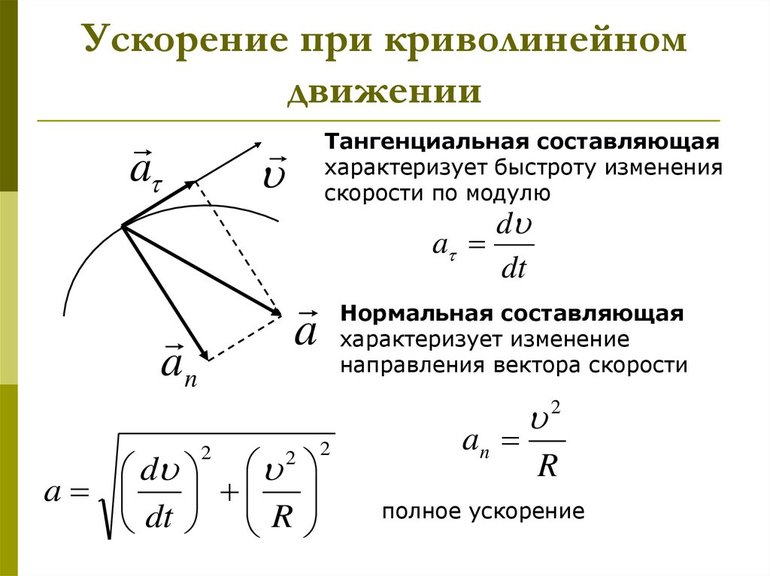
Тангенциальная составляющая ускорения
т.е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю.
называется нормальной составляющей ускорения и направлена по нормали к траектории к центру ее кривизны. Поэтому эту составляющую ускорения называют также центростремительным ускорением.
Таким образом, полное ускорение тела a есть геометрическая сумма тангенциальной aτ и нормальной an составляющих
Тангенциальное ускорение равно первой производной по времени от модуля скорости и определяет быстроту изменения скорости по модулю, и направлено по касательной к траектории.
Нормальное ускорение определяет быстроту изменения скорости по направлению и направлено к центру кривизны траектории.
Векторы aτ и an взаимно перпендикулярны поэтому модуль полного ускорения равен
1.5. Классификация движений материальной точки
В зависимости от тангенциальной и нормальной составляющих ускорения движение можно классифицировать следующим образом:
3) aτ= ƒ(t), an=0 − прямолинейное движение с переменным ускорением.
5) aτ=const, an≠const − равнопеременное движение по окружности.
6) aτ=0, an≠0 − равномерное криволинейное движение.
7) aτ=const, an≠0 − криволинейное равнопеременное движение.
1.6. Кинематика абсолютно твердого тела
Угловой скоростью тела называется вектор, численно равный первой производной по времени от угла поворота тела по времени и направленный вдоль оси вращения по правилу правого винта:
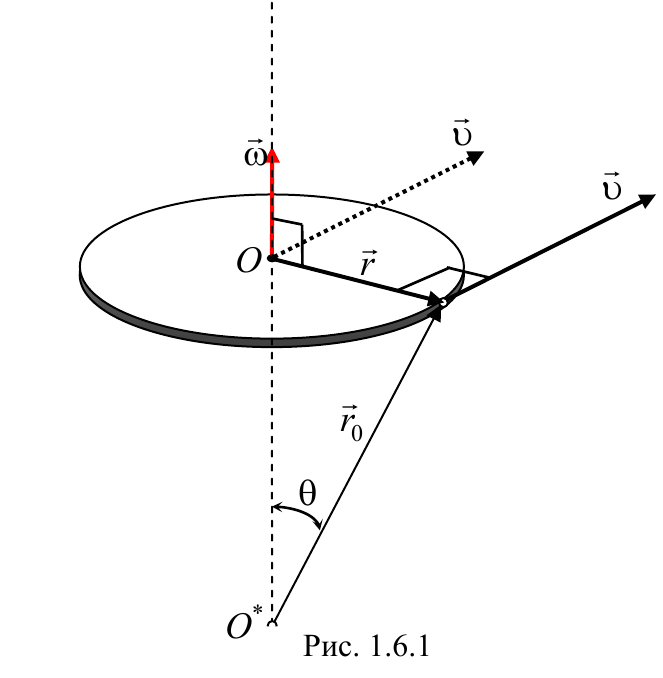
Вектор угловой скорости направлен по оси вращения, причем так, чтобы вращение, рассматриваемое с конца вектора угловой скорости, происходило против хода часовой стрелки (рис 1.6.1). Единицей угловой скорости является рад/с.
Скорость произвольной точки вращающегося тела называется линейной скоростью этой точки.
Равномерное вращение характеризуется периодом вращения и частотой вращения.
Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:
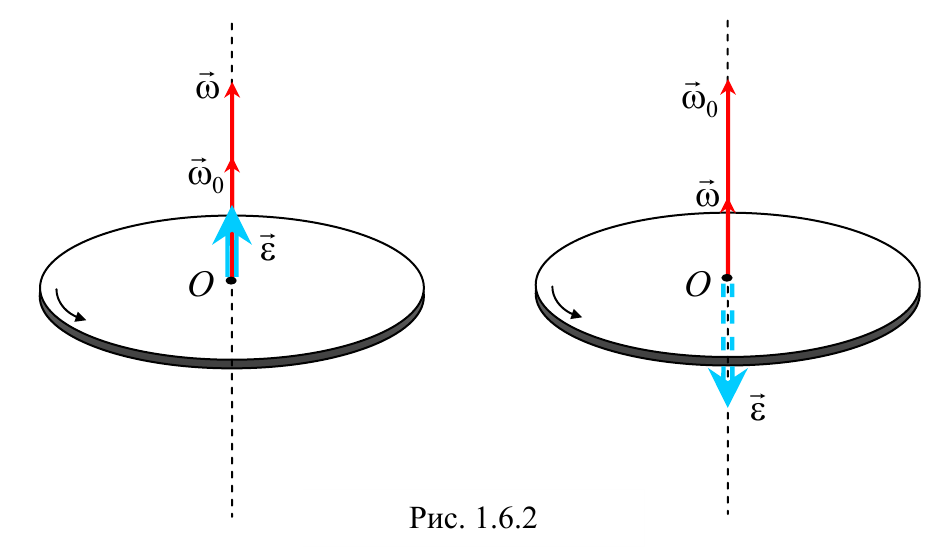
При ускоренном вращении вектор углового ускорения сонаправлен с вектором угловой скорости, а при замедленном − противоположен ему.
В случае равнопеременного движения точки по окружности (ε = const) угловая скорость определяется по формуле
Или в скалярном виде
Проинтегрировав выражение (1.6.1) можно получить формулу для угла поворота тела
1.7. Связь между линейными и угловыми характеристиками тела при его вращении
Тангенциальная и нормальная составляющие ускорения произвольной точки тела, вращающегося вокруг неподвижной оси, определяются формулами:
Ускорение
Ускорение – это величина, которая характеризует быстроту изменения скорости.
Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).
Среднее ускорение
Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:
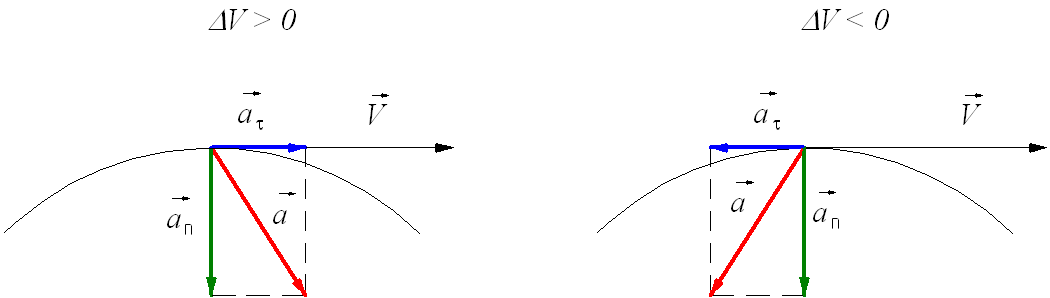
При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть
а направление вектора ускорения совпадает с вектором скорости
Если скорость тела по модулю уменьшается, то есть
то направление вектора ускорения противоположно направлению вектора скорости 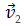
Рис. 1.9. Мгновенное ускорение.
При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).
Тангенциальное ускорение
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Рис. 1.10. Тангенциальное ускорение.
Направление вектора тангенциального ускорения 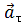
Нормальное ускорение
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой 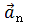
Полное ускорение
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
(согласно теореме Пифагора для прямоугольно прямоугольника).
Направление полного ускорения также определяется правилом сложения векторов:
Что такое тангенциальная скорость
лЙОЕНБФЙЛБ ЙЪХЮБЕФ ТБЪМЙЮОЩЕ НЕИБОЙЮЕУЛЙЕ ДЧЙЦЕОЙС ФЕМ ВЕЪ ТБУУНПФТЕОЙС РТЙЮЙО ЧЩЪЩЧБАЭЙИ ЬФЙ ДЧЙЦЕОЙС.
1.1.1 лЙОЕНБФЙЛБ РПУФХРБФЕМШОПЗП ДЧЙЦЕОЙС
рТЙ РПУФХРБФЕМШОПН ДЧЙЦЕОЙЙ ФЕМБ ЧУЕ ФПЮЛЙ ФЕМБ ДЧЙЦХФУС ПДЙОБЛПЧП, Й, ЧНЕУФП ФПЗП ЮФПВЩ ТБУУНБФТЙЧБФШ ДЧЙЦЕОЙЕ ЛБЦДПК ФПЮЛЙ ФЕМБ, НПЦОП ТБУУНБФТЙЧБФШ ДЧЙЦЕОЙЕ ФПМШЛП ПДОПК ЕЗП ФПЮЛЙ.
пУОПЧОЩЕ ИБТБЛФЕТЙУФЙЛЙ ДЧЙЦЕОЙС НБФЕТЙБМШОПК ФПЮЛЙ: ФТБЕЛФПТЙС ДЧЙЦЕОЙС, РЕТЕНЕЭЕОЙЕ ФПЮЛЙ, РТПКДЕООЩК ЕА РХФШ, ЛППТДЙОБФЩ, УЛПТПУФШ Й ХУЛПТЕОЙЕ.
мЙОЙА, РП ЛПФПТПК ДЧЙЦЕФУС НБФЕТЙБМШОБС ФПЮЛБ Ч РТПУФТБОУФЧЕ, ОБЪЩЧБАФ ФТБЕЛФПТЙЕК.
рЕТЕНЕЭЕОЙЕН НБФЕТЙБМШОПК ФПЮЛЙ ЪБ ОЕЛПФПТЩК РТПНЕЦХФПЛ ЧТЕНЕОЙ ОБЪЩЧБЕФУС ЧЕЛФПТ РЕТЕНЕЭЕОЙС ∆r=r-r0, ОБРТБЧМЕООЩК ПФ РПМПЦЕОЙС ФПЮЛЙ Ч ОБЮБМШОЩК НПНЕОФ ЧТЕНЕОЙ Л ЕЕ РПМПЦЕОЙА Ч ЛПОЕЮОЩК НПНЕОФ.
уЛПТПУФШ НБФЕТЙБМШОПК ФПЮЛЙ РТЕДУФБЧМСЕФ УПВПК ЧЕЛФПТ, ИБТБЛФЕТЙЪХАЭЙК ОБРТБЧМЕОЙЕ Й ВЩУФТПФХ РЕТЕНЕЭЕОЙС НБФЕТЙБМШОПК ФПЮЛЙ ПФОПУЙФЕМШОП ФЕМБ ПФУЮЕФБ. чЕЛФПТ ХУЛПТЕОЙС ИБТБЛФЕТЙЪХЕФ ВЩУФТПФХ Й ОБРТБЧМЕОЙЕ ЙЪНЕОЕОЙС УЛПТПУФЙ НБФЕТЙБМШОПК ФПЮЛЙ ПФОПУЙФЕМШОП ФЕМБ ПФУЮЕФБ.
1.1.2 тБЧОПНЕТОПЕ РТСНПМЙОЕКОПЕ ДЧЙЦЕОЙЕ
тБЧОПНЕТОЩН РТСНПМЙОЕКОЩН ДЧЙЦЕОЙЕН ОБЪЩЧБЕФУС ФБЛПЕ РТСНПМЙОЕКОПЕ ДЧЙЦЕОЙЕ, РТЙ ЛПФПТПН НБФЕТЙБМШОБС ФПЮЛБ (ФЕМП) ДЧЙЦЕФУС РП РТСНПК Й Ч МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ УПЧЕТЫБЕФ ПДЙОБЛПЧЩЕ РЕТЕНЕЭЕОЙС.
чЕЛФПТ УЛПТПУФЙ ТБЧОПНЕТОПЗП РТСНПМЙОЕКОПЗП ДЧЙЦЕОЙС НБФЕТЙБМШОПК ФПЮЛЙ ОБРТБЧМЕО ЧДПМШ ЕЕ ФТБЕЛФПТЙЙ Ч УФПТПОХ ДЧЙЦЕОЙС. чЕЛФПТ УЛПТПУФЙ РТЙ ТБЧОПНЕТОПН РТСНПМЙОЕКОПН ДЧЙЦЕОЙЙ ТБЧЕО ЧЕЛФПТХ РЕТЕНЕЭЕОЙС ЪБ МАВПК РТПНЕЦХФПЛ ЧТЕНЕОЙ, РПДЕМЕООПНХ ОБ ЬФПФ РТПНЕЦХФПЛ ЧТЕНЕОЙ:
рТЙНЕН МЙОЙА, РП ЛПФПТПК ДЧЙЦЕФУС НБФЕТЙБМШОБС ФПЮЛБ, ЪБ ПУШ ЛППТДЙОБФ пи, РТЙЮЕН ЪБ РПМПЦЙФЕМШОПЕ ОБРТБЧМЕОЙЕ ПУЙ ЧЩВЕТЕН ОБРТБЧМЕОЙЕ ДЧЙЦЕОЙС ФПЮЛЙ. фПЗДБ, УРТПЕГЙТПЧБЧ ЧЕЛФПТЩ r Й v, ОБ ЬФХ ПУШ, ДМС РТПЕЛГЙК ∆rx = |∆r| Й ∆vx = |∆v| ЬФЙИ ЧЕЛФПТПЧ НЩ НПЦЕН ЪБРЙУБФШ:
ф.Л. РТЙ ТБЧОПНЕТОПН РТСНПМЙОЕКОПН ДЧЙЦЕОЙЙ S = |∆r|, НПЦЕН ЪБРЙУБФШ: Sx = vx · t. фПЗДБ ДМС ЛППТДЙОБФЩ ФЕМБ Ч МАВПК НПНЕОФ ЧТЕНЕОЙ ЙНЕЕН:
рТЙНЕТ 2.мПДПЮОЙЛ РЕТЕЧПЪЙФ РБУУБЦЙТПЧ У ПДОПЗП ВЕТЕЗБ ОБ ДТХЗПК ЪБ ЧТЕНС t =10 НЙО. РП ФТБЕЛФПТЙЙ бч. уЛПТПУФШ ФЕЮЕОЙС ТЕЛЙ vТ = 0,3 Н/У, ЫЙТЙОБ ТЕЛЙ 240 Н. у ЛБЛПК УЛПТПУФША v ПФОПУЙФЕМШОП ЧПДЩ Й РПД ЛБЛЙН ХЗМПН α Л ВЕТЕЗХ ДПМЦОБ ДЧЙЗБФШУС МПДЛБ, ЮФПВЩ ДПУФЙЮШ ДТХЗПЗП ВЕТЕЗБ ЪБ ХЛБЪБООПЕ ЧТЕНС?
тЕЫЕОЙЕ: рТЙНЕН ВЕТЕЗ ЪБ ОЕРПДЧЙЦОХА УЙУФЕНХ ПФУЮЕФБ. фПЗДБ ПФОПУЙФЕМШОП ВЕТЕЗБ УЛПТПУФШ МПДЛЙ ТБЧОБ:
ьФБ УЛПТПУФШ (ТЙУХОПЛ 1.1), СЧМСЕФУС УХННПК ДЧХИ УЛПТПУФЕК: УЛПТПУФЙ МПДЛЙ ПФОПУЙФЕМШОП ЧПДЩ v’ (УЛПТПУФЙ ПФОПУЙФЕМШОП РПДЧЙЦОПК УЙУФЕНЩ ПФУЮЕФБ) Й УЛПТПУФЙ ТЕЛЙ vТ (УЛПТПУФЙ УБНПК РПДЧЙЦОПК УЙУФЕНЩ ПФУЮЕФБ ПФОПУЙФЕМШОП ОЕРПДЧЙЦОПК). рП ЪБЛПОХ УМПЦЕОЙС УЛПТПУФЕК: v =vТ + v’. фБЛ ЛБЛ РП ХУМПЧЙА ЪБДБЮЙ УЛПТПУФШ МПДЛЙ ПФОПУЙФЕМШОП ВЕТЕЗБ ОБРТБЧМЕОБ ЧДПМШ бч, Б УЛПТПУФШ ТЕЛЙ РЕТРЕОДЙЛХМСТОП бч, ФП УЛПТПУФШ МПДЛЙ ПФОПУЙФЕМШОП ЧПДЩ(РП ФЕПТЕНЕ рЙЖБЗПТБ):
йУЛПНЩК ХЗПМ НПЦОП ОБКФЙ ЙЪ ЧЩТБЦЕОЙС:

1.1.3 оЕТБЧОПНЕТОПЕ ДЧЙЦЕОЙЕ
дЧЙЦЕОЙЕ, РТЙ ЛПФПТПН ЪБ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ФЕМП УПЧЕТЫБЕФ ОЕТБЧОЩЕ РЕТЕНЕЭЕОЙС ОБЪЩЧБАФ ОЕТБЧОПНЕТОЩН ЙМЙ РЕТЕНЕООЩН. уТЕДОЕК УЛПТПУФША vУТ ОБЪЩЧБЕФУС ЧЕМЙЮЙОБ, ТБЧОБС ПФОПЫЕОЙА РЕТЕНЕЭЕОЙС ФЕМБ ∆r ЪБ ОЕЛПФПТЩК РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t Л ЬФПНХ РТПНЕЦХФЛХ:
нПДХМШ УТЕДОЕК УЛПТПУФЙ ПРТЕДЕМСЕФУС ЛБЛ ПФОПЫЕОЙЕ РХФЙ ∆S, РТПКДЕООПЗП ФЕМПН ЪБ ОЕЛПФПТЩК РТПНЕЦХФПЛ ЧТЕНЕОЙ, Л ЬФПНХ РТПНЕЦХФЛХ:
оБРТБЧМЕОЙЕ ЧЕЛФПТБ УТЕДОЕК УЛПТПУФЙ vУТ УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН ∆r (ТЙУХОПЛ 1.2).
рТЙ ОЕПЗТБОЙЮЕООПН ХНЕОШЫЕОЙЙ ∆t, vУТ УФТЕНЙФУС Л РТЕДЕМШОПНХ ЪОБЮЕОЙА, ЛПФПТПЕ ОБЪЩЧБЕФУС НЗОПЧЕООПК УЛПТПУФША. йФБЛ, НЗОПЧЕООБС УЛПТПУФШ v ЕУФШ РТЕДЕМ, Л ЛПФПТПНХ УФТЕНЙФУС УТЕДОСС УЛПТПУФШ vУТ, ЛПЗДБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ДЧЙЦЕОЙС УФТЕНЙФУС Л ОХМА:
йЪ ЛХТУБ НБФЕНБФЙЛЙ ЙЪЧЕУФОП, ЮФП РТЕДЕМ ПФОПЫЕОЙС РТЙТБЭЕОЙС ЖХОЛГЙЙ Л РТЙТБЭЕОЙА БТЗХНЕОФБ, ЛПЗДБ РПУМЕДОЙК УФТЕНЙФУС Л ОХМА РТЕДУФБЧМСЕФ УПВПК РЕТЧХА РТПЙЪЧПДОХА ЬФПК ЖХОЛГЙЙ РП ДБООПНХ БТЗХНЕОФХ. рПЬФПНХ:
рП НЕТЕ ХНЕОШЫЕОЙЕ ∆t РХФШ ∆S ЧУЕ ВПМШЫЕ ВХДЕФ РТЙВМЙЦБФШУС Л |∆r|, РПЬФПНХ НПДХМШ НЗОПЧЕООПК УЛПТПУФЙ:
фБЛЙН ПВТБЪПН, НПДХМШ НЗОПЧЕООПК УЛПТПУФЙ v ТБЧЕО РЕТЧПК РТПЙЪЧПДОПК РХФЙ РП ЧТЕНЕОЙ :
рТЙ ОЕТБЧОПНЕТОПН ДЧЙЦЕОЙЙ ФЕМБ ЕЗП УЛПТПУФШ ОЕРТЕТЩЧОП ЙЪНЕОСЕФУС. лБЛ ВЩУФТП ЙЪНЕОСЕФУС УЛПТПУФШ ФЕМБ, РПЛБЪЩЧБЕФ ЧЕМЙЮЙОБ, ЛПФПТБС ОБЪЩЧБЕФУС ХУЛПТЕОЙЕН. уТЕДОЙН ХУЛПТЕОЙЕН ОЕТБЧОПНЕТОПЗП ДЧЙЦЕОЙС Ч ЙОФЕТЧБМЕ ПФ t ДП t + ∆t ОБЪЩЧБЕФУС ЧЕЛФПТОБС ЧЕМЙЮЙОБ, ТБЧОБС ПФОПЫЕОЙА ЙЪНЕОЕОЙС УЛПТПУФЙ ∆v Л ЙОФЕТЧБМХ ЧТЕНЕОЙ ∆t:
нЗОПЧЕООЩН ХУЛПТЕОЙЕН Б Ч НПНЕОФ ЧТЕНЕОЙ t ВХДЕФ РТЕДЕМ УТЕДОЕЗП ХУЛПТЕОЙС:
фБЛЙН ПВТБЪПН, ХУЛПТЕОЙЕ ∆Б ЕУФШ ЧЕЛФПТОБС ЧЕМЙЮЙОБ, ТБЧОБС РЕТЧПК РТПЙЪЧПДОПК УЛПТПУФЙ РП ЧТЕНЕОЙ. ч ДБООПК УЙУФЕНЕ ПФУЮЕФБ ЧЕЛФПТ ХУЛПТЕОЙС НПЦЕФ ВЩФШ ЪБДБО РТПЕЛГЙСНЙ ОБ УППФЧЕФУФЧХАЭЙЕ ЛППТДЙОБФОЩЕ ПУЙ (РТПЕЛГЙСНЙ БИ, БХ, Бz).
 Б) |  В) | ||||||
 тЕЫЕОЙЕ: рХУФШ ПУШ пи УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН ДЧЙЦЕОЙС РЕТЧПЗП ЧЕМПУЙРЕДЙУФБ, Б ОБЮБМП ЛППТДЙОБФ У ФПЮЛПК O, Ч ЛПФПТПК ПО ОБИПДЙМУС Ч НПНЕОФ ЧТЕНЕОЙ t = 0 (ТЙУХОПЛ 1.4). фПЗДБ ХТБЧОЕОЙС ДЧЙЦЕОЙС ЧЕМПУЙРЕДЙУФБ ФБЛПЧЩ : ч НПНЕОФ ЧУФТЕЮЙ Ч ФПЮЛЕ б: t = t1; x1 = x2. фПЗДБ РПМХЮЙН ТБЧЕОУФЧП:
пРТЕДЕМЙН РЕТЕНЕЭЕОЙЕ ЛБЦДПЗП ДП ЧУФТЕЮЙ. 1.1.5 уЧПВПДОПЕ РБДЕОЙЕ ФЕМ. дЧЙЦЕОЙЕ ФЕМБ, ВТПЫЕООПЗП ЧЕТФЙЛБМШОП ЧЧЕТИрХФШ h, РТПКДЕООЩК ФЕМПН Ч УЧПВПДОПН РБДЕОЙЙ, Л НПНЕОФХ ЧТЕНЕОЙ t: нПДХМШ УЛПТПУФЙ ФЕМБ РПУМЕ РТПИПЦДЕОЙС Ч УЧПВПДОПН РБДЕОЙЙ РХФЙ h ОБИПДЙФУС ЙЪ ЖПТНХМЩ: рТПДПМЦЙФЕМШОПУФШ ∆t УЧПВПДОПЗП РБДЕОЙС ВЕЪ ОБЮБМШОПК УЛПТПУФЙ (v0 = 0) У ЧЩУПФЩ h: рТЙНЕТ 1. фЕМП РБДБЕФ ЧЕТФЙЛБМШОП ЧОЙЪ У ЧЩУПФЩ 20 Н ВЕЪ ОБЮБМШОПК УЛПТПУФЙ. пРТЕДЕМЙФШ: 1) РХФШ h, РТПКДЕООЩК ФЕМПН ЪБ РПУМЕДОАА УЕЛХОДХ РБДЕОЙС, 2) УТЕДОАА УЛПТПУФШ РБДЕОЙС vУТ, 3) УТЕДОАА УЛПТПУФШ ОБ ЧФПТПК РПМПЧЙОЕ РХФЙ vУТ2. |  тЕЫЕОЙЕ: оБРТБЧЙН ПУШ Х ЧЕТФЙЛБМШОП ЧОЙЪ, Й РХУФШ ОБЮБМП ЛППТДЙОБФ УПЧРБДБЕФ У ОБЮБМШОЩН РПМПЦЕОЙЕН ФЕМБ (ТЙУХОПЛ 1.5). 1) уПЗМБУОП ЖПТНХМЕ: ХТБЧОЕОЙЕ ДЧЙЦЕОЙС ЪБРЙЫЕФУС Ч ЧЙДЕ: Ч НПНЕОФ РБДЕОЙС ОБ ЪЕНМА Х = h0. пФУАДБ ЧТЕНС ДЧЙЦЕОЙС ФЕМБ: рХФШ ЪБ РПУМЕДОАА УЕЛХОДХ ТБЧЕО: 2) фЕМП РТПЫМП РХФШ h0. чТЕНС ДЧЙЦЕОЙС
3) дМС ПРТЕДЕМЕОЙС УТЕДОЕК УЛПТПУФЙ ОБ ЧФПТПК РПМПЧЙОЕ РХФЙ, ОЕПВИПДЙНП ХЪОБФШ ЧТЕНС, ЪБ ЛПФПТПЕ ЬФБ ЮБУФШ РХФЙ РТПКДЕОБ. чТЕНС ДЧЙЦЕОЙС ОБ ЧФПТПК РПМПЧЙОЕ РХФЙ ТБЧОП РПМОПНХ ЧТЕНЕОЙ РПМЕФБ t НЙОХУ ЧТЕНС t1, ЪБФТБЮЕООПЕ ОБ РТПИПЦДЕОЙЕ РЕТЧПК РПМПЧЙОЩ РХФЙ. чТЕНС t1 ОБИПДЙФУС ЙЪ ХТБЧОЕОЙС: | ,Ф.Е. |  |
 |
 |
уЛПТПУФШ ФЕМБ Ч РТПЙЪЧПМШОЩК НПНЕОФ ЧТЕНЕОЙ t ПФ ОБЮБМБ ДЧЙЦЕОЙС ОЕЪБЧЙУЙНП ПФ ФПЗП, ТБУУНБФТЙЧБЕФУС МЙЫШ РПДЯЕН ФЕМБ ЙМЙ ЕЗП ПРХУЛБОЙЕ РПУМЕ ДПУФЙЦЕОЙС ОБЙЧЩУЫЕК ФПЮЛЙ, ТБЧОБ v = v0 + g·t.
нБЛУЙНБМШОБС ЧЩУПФБ РПДЯЕНБ ФЕМБ ОБД ФПЮЛПК ВТПУБОЙС:
1.1.6 дЧЙЦЕОЙЕ ФЕМБ, ВТПЫЕООПЗП РПД ХЗМПН Л ЗПТЙЪПОФХ Й ВТПЫЕООПЗП ЗПТЙЪПОФБМШОП У ОЕЛПФПТПК ЧЩУПФЩ
хТБЧОЕОЙЕ ДЧЙЦЕОЙС РП ПУСН пИ Й пХ:
уЛПТПУФШ ФЕМБ Ч МАВПК ФПЮЛЕ ФТБЕЛФПТЙЙ НПЦОП ПРТЕДЕМЙФШ РП ЖПТНХМЕ:
рТЙНЕТ 1. у ВБЫОЙ ЧЩУПФПК о = 25 Н ЗПТЙЪПОФБМШОП ВТПЫЕО ЛБНЕОШ УП УЛПТПУФША υ0 = 15 Н/У. оБКФЙ: УЛПМШЛП ЧТЕНЕОЙ ЛБНЕОШ ВХДЕФ Ч ДЧЙЦЕОЙЙ; ОБ ЛБЛПН ТБУУФПСОЙЙ Sx ПФ ПУОПЧБОЙЙ ВБЫОЙ ПО ХРБДЕФ ОБ ЪЕНМА; У ЛБЛПК УЛПТПУФША υ ПО ХРБДЕФ ОБ ЪЕНМА; ЛБЛПК ХЗПМ φ УПУФБЧЙФ ФТБЕЛФПТЙС ЛБНОС У ЗПТЙЪПОФПН Ч ФПЮЛЕ ЕЗП РБДЕОЙС ОБ ЪЕНМА.
рЕТЕНЕЭЕОЙЕ ВТПЫЕООПЗП ЗПТЙЪПОФБМШОП ЛБНОС НПЦОП ТБЪМПЦЙФШ ОБ ДЧБ (ТЙУХОПЛ 1.7): ЗПТЙЪПОФБМШОПЕ Sx Й ЧЕТФЙЛБМШОПЕ Sy.
рТЙНЕОСС ЪБЛПО ОЕЪБЧЙУЙНПУФЙ ДЧЙЦЕОЙС, ЙНЕЕН:


1)

2) Sx = L = v0·t = 15 · 2,26 = 33,9 Н;
3) vХ = g · t = 9,81 · 2,26 = 22,1 Н/У,
4)

уЛПТПУФШ ФЕМБ Ч МАВПК ФПЮЛЕ ФТБЕЛФПТЙЙ:
рТЙНЕТ 2. фЕМП ВТПЫЕОП РПД ХЗМПН α Л ЗПТЙЪПОФХ У ОБЮБМШОПК УЛПТПУФША υ0. пРТЕДЕМЙФШ ЧТЕНС РПМЕФБ t, НБЛУЙНБМШОХА ЧЩУПФХ о РПДЯЕНБ Й ДБМШОПУФШ L РПМЕФБ.
вХДЕН ТБУУНБФТЙЧБФШ ЧЕТФЙЛБМШОХА Й ЗПТЙЪПОФБМШОХА УПУФБЧМСАЭЙЕ ДЧЙЦЕОЙС ФЕМБ РП ПФДЕМШОПУФЙ, ДМС ЬФПЗП ТБЪМПЦЙН ЧЕЛФПТ ОБЮБМШОПК УЛПТПУФЙ ОБ ЧЕТФЙЛБМШОХА ( υ0·Sinα ) Й ЗПТЙЪПОФБМШОХА ( υ0·Cosα ) УПУФБЧМСАЭЙЕ (ТЙУХОПЛ 1.9).
чЕТФЙЛБМШОБС УЛПТПУФШ ФЕМБ Ч ОБЙЧЩУЫЕК ФПЮЛЕ ФТБЕЛФПТЙЙ (РТЙ t = t1) ТБЧОБ ПЮЕЧЙДОП ОХМА. у ДТХЗПК УФПТПОЩ, ЬФБ УЛПТПУФШ НПЦЕФ ВЩФШ ЧЩТБЦЕОБ РТЙ РПНПЭЙ ЖПТНХМЩ ЪБЧЙУЙНПУФЙ УЛПТПУФЙ ТБЧОПЪБНЕДМЕООПЗП ДЧЙЦЕОЙС ПФ ЧТЕНЕОЙ.
чТЕНС УРХУЛБ t2 НПЦОП ЧЩЮЙУМЙФШ, ТБУУНПФТЕЧ РБДЕОЙЕ ФЕМБ У ЙЪЧЕУФОПК ЧЩУПФЩ о ВЕЪ ОБЮБМШОПК ЧЕТФЙЛБМШОПК УЛПТПУФЙ:
рПМОПЕ ЧТЕНС РПМЕФБ:
дМС ОБИПЦДЕОЙС ДБМШОПУФЙ РПМЕФБ L ОЕПВИПДЙНП ПВТБФЙФШУС Л ЗПТЙЪПОФБМШОПК УПУФБЧМСАЭЕК ДЧЙЦЕОЙС ФЕМБ. лБЛ ХЦЕ ПФНЕЮБМПУШ, РП ЗПТЙЪПОФБМЙ ФЕМП РЕТЕНЕЭБЕФУС ТБЧОПНЕТОП.
1.1.7 тБЧОПРЕТЕНЕООПЕ ДЧЙЦЕОЙЕ ФПЮЛЙ РП ПЛТХЦОПУФЙ
дЧЙЦЕОЙЕ РП ПЛТХЦОПУФЙ СЧМСЕФУС РТПУФЕКЫЙН РТЙНЕТПН ЛТЙЧПМЙОЕКОПЗП ДЧЙЦЕОЙС. уЛПТПУФШ υ ДЧЙЦЕОЙС РП ПЛТХЦОПУФЙ ОБЪЩЧБЕФУС МЙОЕКОПК (ПЛТХЦОПК) УЛПТПУФША. рТЙ ТБЧОПНЕТОПН ДЧЙЦЕОЙЙ РП ПЛТХЦОПУФЙ НПДХМШ НЗОПЧЕООПК УЛПТПУФЙ НБФЕТЙБМШОПК ФПЮЛЙ У ФЕЮЕОЙЕН ЧТЕНЕОЙ ОЕ ЙЪНЕОСЕФУС. дЧЙЦХЭБСУС ФПЮЛБ ЪБ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ РТПИПДЙФ ТБЧОЩЕ РП ДМЙОЕ ДХЗЙ ПЛТХЦОПУФЙ. фБОЗЕОГЙБМШОПЕ ХУЛПТЕОЙЕ РТЙ ТБЧОПНЕТОПН ДЧЙЦЕОЙЙ ФПЮЛЙ РП ПЛТХЦОПУФЙ ПФУХФУФЧХЕФ ( aτ ). йЪНЕОЕОЙЕ ЧЕЛФПТБ УЛПТПУФЙ υ РП ОБРТБЧМЕОЙА ИБТБЛФЕТЙЪХЕФУС ОПТНБМШОЩН ХУЛПТЕОЙЕН an, ЛПФПТПЕ ОБЪЩЧБЕФУС ФБЛЦЕ ГЕОФТПУФТЕНЙФЕМШОЩН ХУЛПТЕОЙЕН.
ч ЛБЦДПК ФПЮЛЕ ФТБЕЛФПТЙЙ ЧЕЛФПТ an ОБРТБЧМЕО РП ТБДЙХУХ Л ГЕОФТХ ПЛТХЦОПУФЙ, Б ЕЗП НПДХМШ ТБЧЕО:
нПДХМШ ЧЕЛФПТБ dφ ТБЧЕО ХЗМХ РПЧПТПФБ. оБРТБЧМЕОЙЕ ЧЕЛФПТБ dφ УПЧРБДБЕФ У ОБРТБЧМЕОЙЕН РПУФХРБФЕМШОПЗП ДЧЙЦЕОЙС ПУФТЙС ЧЙОФБ, ЗПМПЧЛБ ЛПФПТПЗП, ЧТБЭБЕФУС Ч ОБРТБЧМЕОЙЙ ДЧЙЦЕОЙС ФПЮЛЙ РП ПЛТХЦОПУФЙ, Ф.Е. РПДЮЙОСЕФУС РТБЧЙМХ РТБЧПЗП ЧЙОФБ (ТЙУХОПЛ 1.12).
CТЕДОЕК ХЗМПЧПК УЛПТПУФША ДЧЙЦЕОЙС ФПЮЛЙ РП ПЛТХЦОПУФЙ ЧПЛТХЗ ПУЙ ОБЪЩЧБЕФУС ЧЕМЙЮЙОБ ωcp, ТБЧОБС ПФОПЫЕОЙА ХЗМБ РПЧПТПФБ ∆φ ТБДЙХУ-ЧЕЛФПТБ ФПЮЛЙ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t Л ДМЙФЕМШОПУФЙ ЬФПЗП РТПНЕЦХФЛБ:
хЗМПЧПК УЛПТПУФША (НЗОПЧЕООПК ХЗМПЧПК УЛПТПУФША) ω ОБЪЩЧБЕФУС РТЕДЕМ, Л ЛПФПТПНХ УФТЕНЙФУС УТЕДОСС ХЗМПЧБС УЛПТПУФШ РТЙ ВЕУЛПОЕЮОПН ХНЕОШЫЕОЙЙ РТПНЕЦХФЛБ ЧТЕНЕОЙ ∆t, ЙМЙ РЕТЧБС РТПЙЪЧПДОБС ПФ ХЗМБ РПЧПТПФБ РП ЧТЕНЕОЙ:
чЕЛФПТ ω ОБРТБЧМЕО ЧДПМШ ПУЙ ЧТБЭЕОЙС РП РТБЧЙМХ РТБЧПЗП ЧЙОФБ, Ф.Е. ФБЛЦЕ ЛБЛ Й dφ (ТЙУХОПЛ 1.13).
рТЙ ТБЧОПНЕТОПН ДЧЙЦЕОЙЙ ФПЮЛЙ РП ПЛТХЦОПУФЙ ЪБ МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ХЗМЩ РПЧПТПФБ ЕЕ ТБДЙХУ-ЧЕЛФПТБ ПДЙОБЛПЧЩ. уМЕДПЧБФЕМШОП, РТЙ ФБЛПН ДЧЙЦЕОЙЙ НЗОПЧЕООБС ХЗМПЧБС УЛПТПУФШ ТБЧОБ УТЕДОЕК ХЗМПЧПК УЛПТПУФЙ: ω = ωcp. хЗПМ РПЧПТПФБ ∆ω ТБДЙХУ-ЧЕЛФПТБ ФПЮЛЙ, ТБЧОПНЕТОП ДЧЙЦХЭЕКУС РП ПЛТХЦОПУФЙ, ТБЧЕО:
рТПНЕЦХФПЛ ЧТЕНЕОЙ ф, Ч ФЕЮЕОЙЙ ЛПФПТПЗП ФПЮЛБ УПЧЕТЫБЕФ ПДЙО РПМОЩК ПВПТПФ РП ПЛТХЦОПУФЙ, ОБЪЩЧБЕФУС РЕТЙПДПН ПВТБЭЕОЙС (РЕТЙПДПН ЧТБЭЕОЙС), Б ЧЕМЙЮЙОБ υ, ПВТБФОБС РЕТЙПДХ:

ЮБУФПФПК ПВТБЭЕОЙС (ЮБУФПФПК ЧТБЭЕОЙС). ъБ ПДЙО РЕТЙПД ХЗПМ РПЧПТПФБ ТБДЙХУ-ЧЕЛФПТБ ФПЮЛЙ ТБЧЕО 2π ТБД, РПЬФПНХ 2π = ωT, ПФЛХДБ T = 2π/ω, ЙМЙ ω = 2π/ф = 2πν.
мЙОЕКОБС υ Й ХЗМПЧБС ω УЛПТПУФЙ УЧСЪБОЩ УППФОПЫЕОЙЕН: υ = ω·R. ьФП ЧЙДОП ЙЪ УМЕДХАЭЕЗП ЧЩЧПДБ:
рТЙНЕТ 1. пРТЕДЕМЙФШ НПДХМШ УЛПТПУФЙ Й ГЕОФТПУФТЕНЙФЕМШОПЗП ХУЛПТЕОЙС ФПЮЕЛ ЪЕНОПК РПЧЕТИОПУФЙ ОБ ЬЛЧБФПТЕ. тБДЙХУ ъЕНМЙ РТЙОСФШ ТБЧОЩН 6400 ЛН.
R = 6400 ЛН = 6,4·10 6 Н;
ф = 24 Ю = 8,64·10 4 У;
тЕЫЕОЙЕ: фПЮЛЙ ЪЕНОПК РПЧЕТИОПУФЙ ОБ ЬЛЧБФПТЕ ДЧЙЦХФУС РП ПЛТХЦОПУФЙ ТБДЙХУБ R, РПЬФПНХ НПДХМШ ЙИ УЛПТПУФЙ:
1.1.8 чТБЭБФЕМШОПЕ ДЧЙЦЕОЙЕ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ЧПЛТХЗ ОЕРПДЧЙЦОПК ПУЙ
дМС ЛЙОЕНБФЙЮЕУЛПЗП ПРЙУБОЙС ЧТБЭБФЕМШОПЗП ДЧЙЦЕОЙС БВУПМАФОП ФЧЕТДПЗП ФЕМБ ЧПЛТХЗ ЛБЛПК-ФП ОЕРПДЧЙЦОПК ПУЙ ЙУРПМШЪХАФУС ФЕ ЦЕ ЧЕМЙЮЙОЩ (Й ХТБЧОЕОЙС УЧСЪЙ НЕЦДХ ОЙНЙ), ЮФП Й ДМС ПРЙУБОЙС ДЧЙЦЕОЙС ФПЮЛЙ РП ПЛТХЦОПУФЙ. рТЙ ЧТБЭБФЕМШОПН ДЧЙЦЕОЙЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ЧПЛТХЗ ОЕРПДЧЙЦОПК ПУЙ ЪБ РТПНЕЦХФПЛ ЧТЕНЕОЙ ∆t ХЗМЩ РПЧПТПФБ ТБДЙХУ-ЧЕЛФПТПЧ ТБЪМЙЮОЩИ ФПЮЕЛ ФЕМБ ПДЙОБЛПЧЩ. хЗПМ РПЧПТПФБ ∆φ, УТЕДОСС ωcp Й НЗОПЧЕООБС ω ХЗМПЧЩЕ УЛПТПУФЙ ИБТБЛФЕТЙЪХАФ ЧТБЭБФЕМШОПЕ ДЧЙЦЕОЙЕ ЧУЕЗП БВУПМАФОП ФЧЕТДПЗП ФЕМБ Ч ГЕМПН.
мЙОЕКОБС УЛПТПУФШ υ ЛБЛПК-МЙВП ФПЮЛЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ РТПРПТГЙПОБМШОП ТБУУФПСОЙА R ФПЮЛЙ ПФ ПУЙ ЧТБЭЕОЙС:
рТЙ ТБЧОПНЕТОПН ЧТБЭБФЕМШОПН ДЧЙЦЕОЙЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ХЗМЩ РПЧПТПФБ ФЕМБ ЪБ МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ПДЙОБЛПЧЩ ( ∆φ = const ) Й НЗОПЧЕООБС ХЗМПЧБС УЛПТПУФШ ФЕМБ ТБЧОБ УТЕДОЕК ХЗМПЧПК УЛПТПУФЙ ( ω = ωcp ). фБОЗЕОГЙБМШОЩЕ ХУЛПТЕОЙС aτ Х ТБЪМЙЮОЩИ ФПЮЕЛ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ПФУХФУФЧХАФ ( aτ = 0 ), Б ОПТНБМШОПЕ (ГЕОФТПУФТЕНЙФЕМШОПЕ ) ХУЛПТЕОЙЕ an ЛБЛПК-МЙВП ФПЮЛЙ ФЕМБ ЪБЧЙУЙФ ПФ ЕЕ ТБУУФПСОЙС R ДП ПУЙ ЧТБЭЕОЙС:
чЕЛФПТ an ОБРТБЧМЕО Ч ЛБЦДЩК НПНЕОФ ЧТЕНЕОЙ РП ТБДЙХУХ ФТБЕЛФПТЙЙ ФПЮЛЙ Л ПУЙ ЧТБЭЕОЙС.
рТЙ ОЕТБЧОПНЕТОПН ЧТБЭБФЕМШОПН ДЧЙЦЕОЙЙ БВУПМАФОП ФЧЕТДПЗП ФЕМБ ХЗМЩ РПЧПТПФБ ФЕМБ ЪБ МАВЩЕ ТБЧОЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ОЕПДЙОБЛПЧЩ. хЗМПЧБС УЛПТПУФШ ФЕМБ ω У ФЕЮЕОЙЕН ЧТЕНЕОЙ ЙЪНЕОСЕФУС.
еУМЙ ХЗМПЧБС УЛПТПУФШ ЪБ РТПЙЪЧПМШОЩЕ ПДЙОБЛПЧЩЕ РТПНЕЦХФЛЙ ЧТЕНЕОЙ ЙЪНЕОСЕФУС ПДЙОБЛПЧП ( ∆ω12 = ∆ω34 Й Ф.Д.), ФП εУТ = const (ТБЧОПРЕТЕНЕООПЕ ЧТБЭЕОЙЕ).
фБОЗЕОГЙБМШОБС УПУФБЧМСАЭБС ХУЛПТЕОЙС:

оПТНБМШОБС УПУФБЧМСАЭБС ХУЛПТЕОЙС:
фБЛЙН ПВТБЪПН, УЧСЪШ НЕЦДХ МЙОЕКОЩНЙ Й ХЗМПЧЩНЙ ЧЕМЙЮЙОБНЙ ЧЩТБЦБЕФУС УМЕДХАЭЙНЙ ЖПТНХМБНЙ: S = R·φ, υ = ω·R, aτ = R·ε, an = ω 2 ·R.




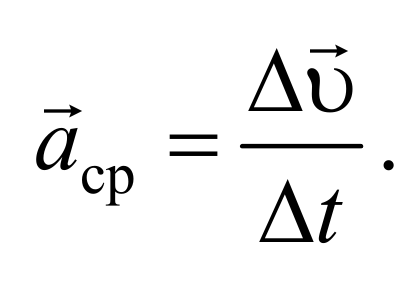
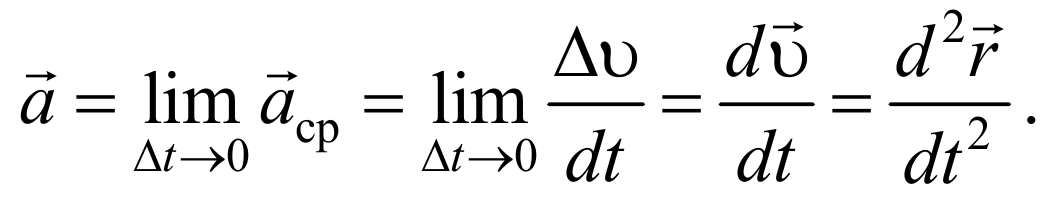
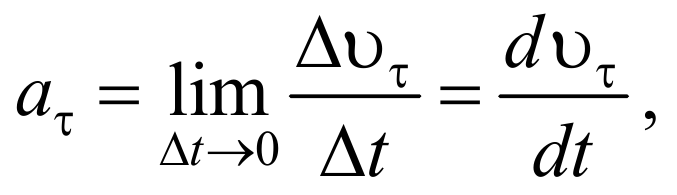
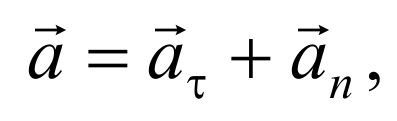
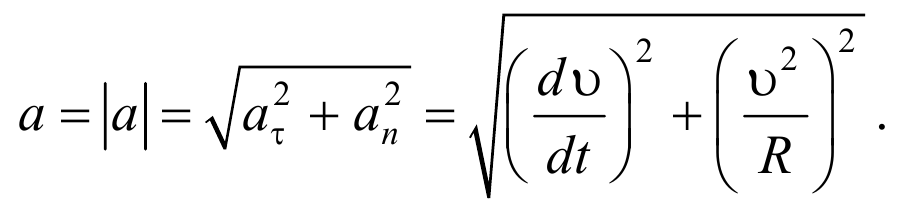
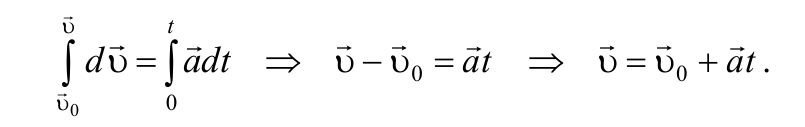
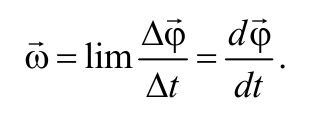
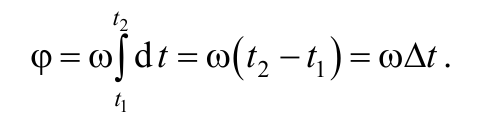
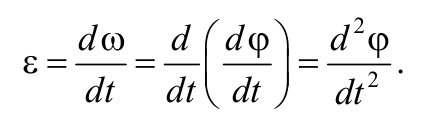
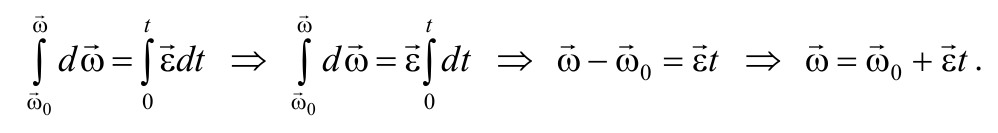
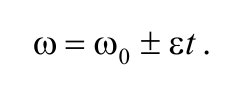
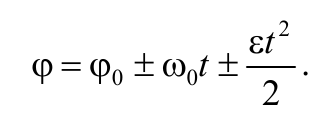
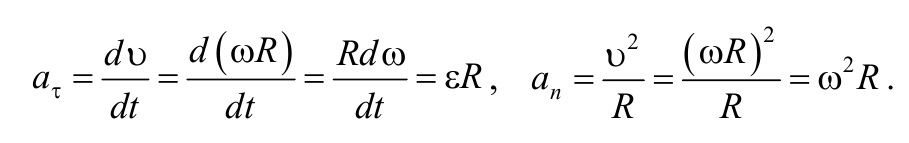
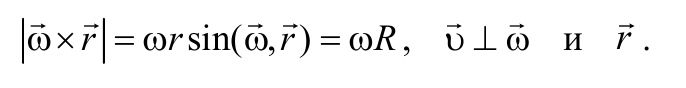



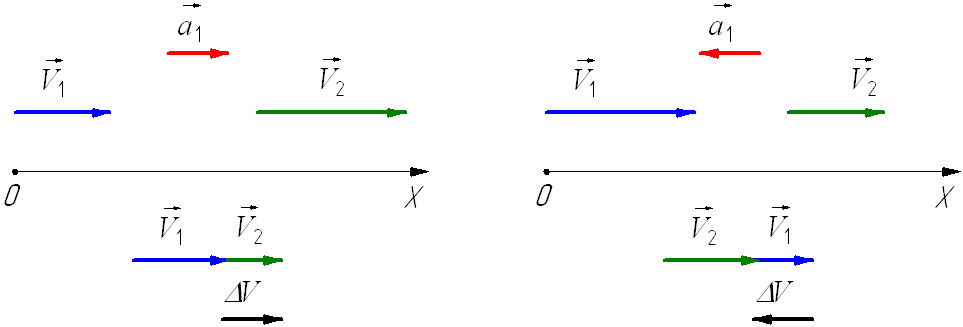
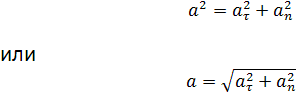

























 , ПФЛХДБ v01·t1 + v02·t1 = И02, Ф.Л. Б1 = Б2,
, ПФЛХДБ v01·t1 + v02·t1 = И02, Ф.Л. Б1 = Б2,


















































