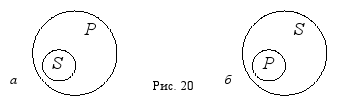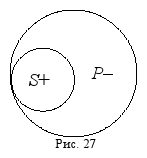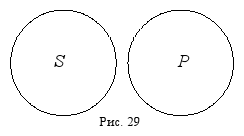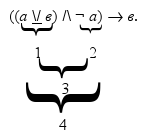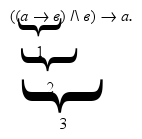что такое суждение кратко
Суждение
Суждение — форма мышления, в которой что-либо утверждается или отрицается о предмете, его свойствах или отношениях между предметами. Виды суждений и отношения между ними изучаются в философской логике.
Содержание
Простые и сложные суждения
Простые суждения — суждения, составными частями которых являются понятия. Простое суждение можно разложить только на понятия.
Сложные суждения — суждения, составными частями которых являются простые суждения или их сочетания. Сложное суждение может рассматриваться как образование из нескольких исходных суждений, соединенных в рамках данного сложного суждения логическими союзами (связками). От того, при помощи какого союза связываются простые суждения, зависит логическая особенность сложного суждения.
Состав простого суждения
Простое (атрибутивное) суждение — это суждение о принадлежности предметам свойств (атрибутов), а также суждения об отсутствии у предметов каких-либо свойств. В атрибутивном суждении могут быть выделены термины суждения — субъект, предикат, связка, квантор.
Состав сложного суждения
Сложные суждения состоят из ряда простых («Человек не стремится к тому, во что не верит, и любой энтузиазм, не подкрепляясь реальными достижениями, постепенно угасает»), каждое из которых в математической логике обозначается латинскими буквами (A, B, C, D… a, b, c, d…). В зависимости от способа образования различают конъюнктивные, дизъюнктивные, импликационные, эквивалентные и отрицательные суждения.
Дизъюнктивные суждения образуются с помощью разделительных (дизъюнктивных) логических связок (аналогичных союзу «или»). Подобно простым разделительным суждениям, они бывают:
Импликационные суждения образуются с помощью импликации, (эквивалентно союзу «если …, то»). Записывается как 

Конъюнктивные суждения образуются с помощью логических связок сочетания или конъюнкции (эквивалентно запятой или союзам «и», «а», «но», «да», «хотя», «который», «зато» и другим). Записывается как 
Эквивалентные суждения указывают на тождественность частей суждения друг другу (проводят между ними знак равенства). Помимо определений, поясняющих какой-либо термин, могут быть представлены суждениями, соединенными союзами «если только», «необходимо», «достаточно» (например: «Чтобы число делилось на 3, достаточно, чтобы сумма цифр, его составляющих, делилась на 3»). Записывается как 

Отрицательные суждения строятся с помощью связок отрицания «не». Записываются либо как a
b, либо как a b (при внутреннем отрицании типа «машина не роскошь»), а также с помощью черты над всем суждением при внешнем отрицании (опровержении): «не верно, что …» (a b).
Классификация простых суждений
По качеству
По объёму
По отношению
По отношению между подлежащим и сказуемым
Субъект и предикат суждения могут быть распределены (индекс «+») или не распределены (индекс «-»).
Суждения А (обще-утвердительные суждения) Распределяет свое подлежащее (S), но не распределяет свое сказуемое (P)
Объем подлежащего (S) меньше объема сказуемого (Р)
Объемы подлежащего и сказуемого совпадают
Суждения Е (обще-отрицательные суждения) Распределяет как подлежащее (S), так и сказуемое (P)
В этом суждении мы отрицаем всякое совпадение между подлежащим и сказуемым
Суждения I (частно-утвердительные суждения) Ни подлежащие (S), ни сказуемые (P) не распределены
Часть класса подлежащего входит в класс сказуемого.
Суждения О (частно-отрицательные суждения) Распределяет свое сказуемое (Р), но не распределяет свое подлежащее (S) В этих суждениях мы обращаем внимание на то, что есть несовпадающего между ними (заштрихованная область)
таблица распределения подлежащего и сказуемого
| Подлежащее (S) | Сказуемое (P) | ||
|---|---|---|---|
| о-у | А | распределено | нераспределено |
| о-о | Е | распределено | распределено |
| ч-у | I | нераспределено | нераспределено |
| ч-о | О | нераспределено | распределено |
Другие
1) S есть или А, или В, или С
2) или А, или В, или С есть Р когда в суждении остается место неопределенности
Если А есть В, то С есть D или Е есть F
если есть А, то есть а, или b, или с Прим: « Если кто желает получить высшее образование, то он должен учиться или в университете, или в институте, или в академии»
Модальность суждений
Модальные понятия, или модальности — понятия, выражающие контекстную рамку суждения: время суждения, место суждения, знание о суждении, отношение говорящего к суждению.
В зависимости от модальности выделяются следующие основные виды суждений:
Урок 4. Суждения и высказывания. Введение в силлогистику

Содержание:
Суждения и высказывания
Что такое рассуждение? Можно было бы сказать: вывод, умозаключение, размышление, доказательство и т.д. Всё это верно, но, пожалуй, самым очевидным ответом было бы: рассуждение – это последовательность суждений, которые в идеале должны быть связаны между собой согласно правилам логики. Поэтому обучение правильному рассуждению нужно начинать с того, что такое суждения и как ими корректно пользоваться.
Суждение – это мысль об утверждении или отрицании наличия некоторой ситуации в мире.
В естественном языке суждения передаются с помощью повествовательных предложений, или высказываний. Примеры суждений, выраженных в высказываниях: «Пришла осень», «Катя не знает английского языка», «Я люблю читать», «Трава зелёная, а небо голубое». Одно и то же суждение может быть выражено с помощь разных высказываний, в частности: «Небо голубое» и «The sky is blue» – разные высказывания, но суждение они выражают одно и то же, так как они передают одну и ту же мысль. Точно также высказывания «Никто не покидал дома» и «Все оставались дома» разные, но они передают одно суждение.
Поскольку высказывания посредством суждений фиксируют какое-то положение дел в мире, в отличие от понятий и определений, мы можем оценивать их с точки зрения их истинности и ложности. Так высказывание «Бил Гейтс основал компанию “Microsoft”» – истинное, а высказывание «Апельсины фиолетовые» – ложное.
Если вспомнить треугольник Фреге, то высказывание будет находиться на вершине, обозначающей знак, суждение будет составлять его смысл, а истина и ложь – значение.
Существует множество типов суждений и, соответственно, высказываний. Разные логические системы концентрируются на их разных аспектах. Силлогистика работает с так называемыми категорическими атрибутивными высказываниями. Категорические высказывания противопоставляются гипотетическим. Гипотетические высказывания говорят о возможности наличия или отсутствия какой-то ситуации в мире: «Возможно, пойдёт дождь». Категорические высказывания безапелляционно утверждают о том, что какая-то ситуация имеется или не имеется: «Пошёл дождь». Термин «атрибутивный» означает, что эти высказывания говорят о наличии либо отсутствии у предмета или класса предметов некоторого свойства. Примеры категорических атрибутивных высказываний: «Моя машина синего цвета», «Парк около нашего дома большой», «Никто не любит рыбий жир», «Некоторые люди считают, что они самые умные». Хотя на первый взгляд может показаться, что из-за концентрации именно на категорических атрибутивных высказываниях, применение силлогистики ограничено, это не так. Огромный пласт рассуждений не выходит за рамки подобных высказываний, а потому знания силлогистики оказывается достаточно для того, чтобы научиться размышлять логично и не давать ввести себя в заблуждение.
Состав и виды категорических атрибутивных высказываний
Категорические атрибутивные высказывания состоят из терминов, предицирующих связок и кванторов.
Термины делятся на субъект и предикат.
Предицирующие связки, как, возможно, вы помните из первого урока, это связки «есть» и «не есть». В естественном языке они могут выражаться с помощью разных слов и конструкций: «есть», «являться», «суть», «это», «выступать», знака тире, глаголов, либо вообще опускаться.
Кванторы – это слова, указывающие на количественные характеристики субъекта. Существует два вида кванторов: квантор общности («все», «каждый», «любой», «ни один», «никто») и квантор существования («некоторые», «не все», «какой-либо», «многие»). Также как и предицирующие связки, кванторы в естественной речи могут опускаться. Мы можем сказать: «Люди равны перед законом», подразумевая, что «Все люди равны перед законом»; или «Дети любят сладкое» – подразумевая, что «Многие дети любят сладкое». Зачастую лучше всего уточнить у вашего собеседника, какой именно квантор он имеет в виду, так как это будет сказываться на условиях истинности его высказываний.
Давайте разберём следующее высказывание: «Кошки мурлычут, когда им приятно». «Кошки» – это субъект, «существа, мурлычущие, когда им приятно» – это предикат. Также здесь присутствует невидимая связка «есть», которая соединяет субъект с предикатом, и невидимый квантор общности «все». Так, если записать это высказывание в соответствии с его логической формой, то получим: «Все кошки есть существа, которые мурлычут, когда им приятно». Благодаря этому примеру становится ясно, что прежде чем определять, истинно высказывание или ложно, нужно выявить его логическую форму и преобразовать исходное высказывание так, чтобы все четыре элемента (квантор, субъект, связка, предикат) были на своих местах.
В зависимости от свойств логических и нелогических терминов, входящих в состав категорических атрибутивных высказываний, их можно разделить на несколько видов.
Если мы скомбинируем эти виды между собой, то получается, что всего существует шесть видов категорических атрибутивных высказываний:
Условия истинности для категорических атрибутивных высказываний в традиционной силлогистике
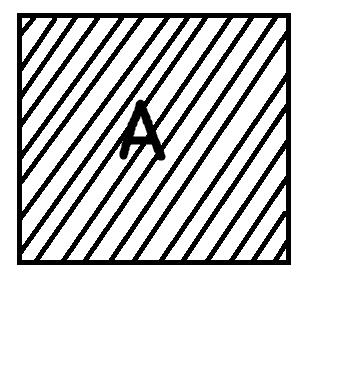
Следует начать с того, что традиционная силлогистика накладывает два ограничения на используемые термины, а именно: они должны быть непусты и неуниверсальны, то есть если под термин не подпадает ни один объект из универсума рассмотрения или, наоборот, подпадают все объекты универсума, то они не могут быть предметом рассмотрения. Посмотрим на рисунки:
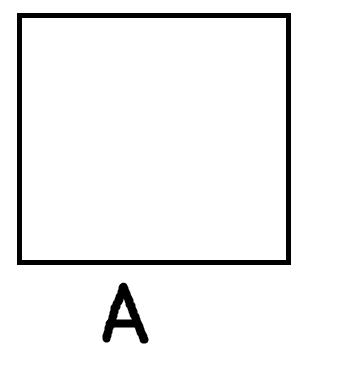
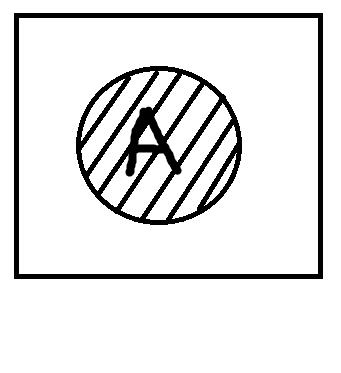
Первый рисунок изображает ситуацию, когда термин А пуст, поэтому весь квадратик (универсум рассмотрения) остался белым. Второй рисунок показывает случай, когда объём термина А совпадает с объёмом универсума рассмотрения, поэтому весь квадрат заштрихован. Последний рисунок репрезентирует термин А, который является непустым и в то же время неуниверсальным. Заштрихованая область соотвествует объёму А. Традиционная силлогистика работает только с терминами, которые соотвествуют третьему рисунку. Такое условие ставится для того, чтобы исключить из рассмотрения высказывания, которые невозможно оценить как истинные либо ложные. Возьмём высказывание: «Все дети Ивана лысые». Вроде бы с высказыванием всё впорядке, однако представьте, что у Ивана нет детей. Мы не можем в данном случае просто сказать, что высказывание ложное. Если назвать его ложным, то тем самым мы подразумеваем, что не все дети Ивана лысые, а это не так. В то же время мы не можем сказать, что оно истинное. Выход из этого затруднительного положения состоит как раз в том, чтобы указать на пустоту термина «дети Ивана». Поскольку у Ивана нет детей, этот термин пуст, и мы не можем построить с ним корректное высказывание.
Непустота и неуниверсальность термина будут определяться не только контекстом, но и выбранным универсумом рассмотрения. Если наш квадратик представляет собой универсум живых существ или материально существующих предметов, то, конечно, такие термины как «русалка», «хоббит», «дракон» и т.п. окажутся пустыми, и мы не сможем их рассматривать. Однако, если универсум рассмотрения – это мифологические или сказочные существа, то все эти термины перестают быть пустыми. То же самое верно и для универсальности. Термин «люди» может рассматриваться как универсальный, что исключает его из области традиционной силлогистики. Однако если мы хотим сказать «Сократ – человек», то в качестве универсума рассмотрения вполне можно взять живых существ. На универсуме живых существ, термин «люди» уже не будет универсальным.
Кроме того, нужно помнить, что субъект и предикат должны задаваться на одном и том же универсуме рассмотрения.
Теперь посмотрим, при каких условиях разные типы категориальных атрибутивных высказываний будут истинными. Для этого советуем ещё раз заглянуть в урок, посвящённый отношениям между понятиями. По большому счёту, субъект и предикат – это термины, представляющие некоторые понятия. Соответственно, если соединить эти понятия в одном предложении с помощью предицирующих связок и кванторов, то, чтобы узнать будут эти предложения истинными или ложными, достаточно посмотреть на диаграммы, иллюстрирующие отношения между этими двумя понятиями. Итак, преступим.
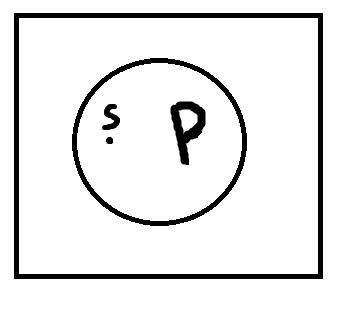
Единичноутвердительные высказывания формы «s есть P» истинны, только если термины s и P находятся в следующем отношении:
Другими словами, единичноутвердительные высказывания истинны, если точка, представляющая собой имя s, находится внутри кружочка, изображающего объём термина P. Например, возьмём высказывание «Лев Толстой проповедовал вегетарианство». «Лев Толстой» – это субъект, имя s. «Человек, проповедующий вегетарианство» – это предикат, термин P. Это высказывание истинно, так как точка s будет входить в объём термина P. Если же взять высказывание «Николай Гоголь – это великий русский композитор», то точка s, представляющая имя («Николай Гоголь»), не будет входить в объём термина P («великие русские композиторы»). Поэтому это высказывание ложно.
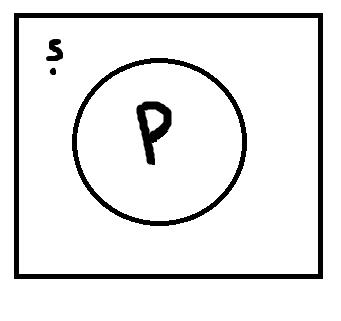
Единичноотрицательные высказывания, имеющие форму «s не есть P» истинны, если термины s и P находятся в следующем отношении:
Как видно из рисунка, здесь имеет место ситуация, прямо противоположная условиям истинности единичноутвердительных высказываний. Если точка, представляющая имя s, находится вне объёма термина P, то высказывание истинно. В обратном случае, оно ложно. Пример истинного единичноотрицательного высказывания: «Александр Пушкин никогда не был во Франции». Ложным единичноотрицательным высказыванием будет: «Иван Бунин не получил Нобелевскую премию по литературе».
Общеутвердительные высказывания формы «Все S есть P» истинны, если термины S и P находятся в одном из следующих отношений:
Первый рисунок изображает отношение равнообъёмности, второй – обратного подчинения. Если объёмы двух терминов совпадают (S и P делят один кружочек) или объём термина S полностью входит в объём термина P (кружочек S полностью включается в P), то общеутвердительное высказывание истинно. Если термины S и P находятся в каком-либо другом отношении, то общеутвердительные высказывания не могут быть истинными. В качестве иллюстрации истинных высказываний можно привести: «Все хвойные растения имеют шишки», «Все киты – это млекопитающие». Пример ложных высказываний: «Все политики – обманщики», «Все девушки мечтают выйти замуж за миллионера». В этих примерах термины, обозначающие субъект и предикат, не находятся ни в одном из указанных выше отношений.
Общеотрицательные высказывания, имеющие форму «Ни один S не есть P» истинны, только если термины S и P находятся в следующих отношениях:
На первом рисунке представлено отношение противоречия, а на втором – соподчинения. Как видно, у S и P нет общих элементов, их объёмы не пересекаются. К примеру, истинными будут высказывания: «Ни один павлин не относится к числу певчих птиц», «Ни один человек младше восемнадцати лет не является совершеннолетним в России». Пример ложного высказывания: «Ни один гуманитарий не разбирается в математике». Высказывание ложно, так как термины «гуманитарий» и «люди, разбирающиеся в математике» не находятся ни в отношении противоречия, ни в отношении соподчинения.
Частноутвердительные высказывания формы «Некоторые S есть P» истинны, если термины S и P находятся в следующих отношениях:
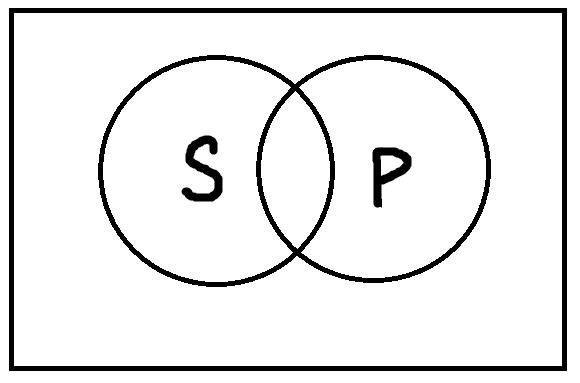

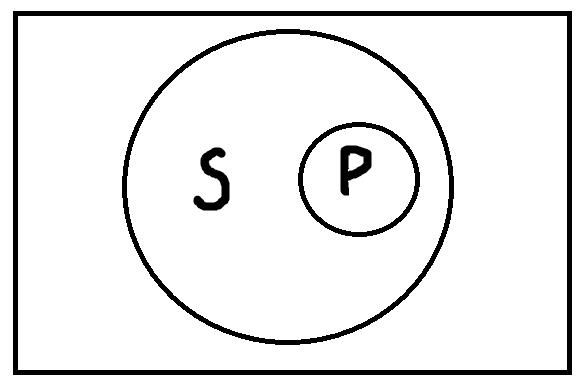
Частноутвердительные высказывания будут ложными, только если термины S и P находятся в отношении противоречия или соподчинения: «Некоторые тракторы – это самолёты», «Некоторые ложные высказывания истинны».
Частноотрицательные высказывания типа «Некоторые S не есть P» истинны, если термины S и P находятся в следующих отношениях:
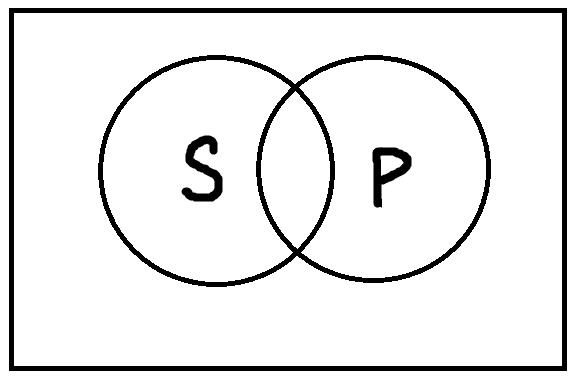

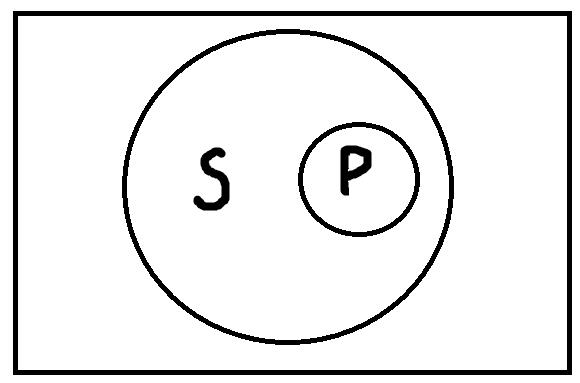
Это отношения: пересечения, дополнительности, включения, противоречия и соподчинения. Очевидно, что первые три отношения совпадают с тем, что было верно и для частноутвердительных высказываний. Все они как раз представляют случаи, когда некоторые S есть P, и в то же время некоторые S не есть P. Примеры подобных истинных высказываний: «Некоторые здоровые люди не употребляют алкоголь», «Некоторые наши работники из категории младше сорока ещё не достигли возраста и двадцати пяти», «Некоторые деревья не являются вечнозелёными».
По тем же причинам, по которым отношения равнообъёмности и обратного подчинения представляли собой условия истинности для частноутвердительных высказываний, отношения противоречия и соподчинения будут верны для частноотрицательных высказываний. Из высказывания, имеющего форму «Некоторые S не есть P» нельзя логично вывести высказывание «Некоторые S есть P». Однако из высказывания «Все S не есть P» можно перейти к высказыванию «Некоторые S не есть P», так как на основании информации, которой мы обладаем обо всех элементах объёмов терминов S и P, можно сделать вывод и об их отдельных представителях. Поэтому верными будут высказывания: «Некоторые журналы не являются книгами», «Некоторые глупцы не являются умными» и т.п.
Частноотрицательные высказывания будут ложными, только если термины S и P находятся в отношениях равнообъёмности и обратного подчинения. Примеры ложных высказываний: «Некоторые рыбы не умеют дышать под водой», «Некоторые яблоки не являются фруктами».
Итак, мы выяснили, при каких условиях высказывания той или иной формы будут истинными и ложными. При этом стало понятно, что не всегда истинность и ложность высказываний с логической точки зрения совпадает с нашими интуитивными представлениями. Иногда одинаковые на первый взгляд высказывания оцениваются совершенно по-разному, так как за ними скрываются разные логические формы и, следовательно, разные отношения между входящими в них терминами. Эти условия истинности важно запомнить. Они пригодятся, когда в следующем уроке мы научимся складывать высказывания в цепочки рассуждений и будем пытаться найти такие формы умозаключений, которые будут всегда правильными.
Игра «Пересечение множеств»
В этом упражнении вам нужно внимательно прочитать текст задания и правильно расположить множества, соответствующие понятиям.
Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.
Упражнения
Прочитайте следующие категориальные атрибутивные высказывания. Определите, к какому типу они относятся. С помощью диаграмм покажите, истинны они или ложны.
Проверьте свои знания
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.
Что такое суждение кратко
2.1. Суждение как форма мышления
Суждение (высказывание) – это форма мышления, в которой что-либо утверждается или отрицается. Например: «Все сосны являются деревьями», «Некоторые люди – это спортсмены», «Ни один кит – не рыба», «Некоторые животные не являются хищниками».
Рассмотрим несколько важных свойств суждения, которые в то же время отличают его от понятия:
1. Любое суждение состоит из понятий, связанных между собой.
Например, если связать понятия «карась» и «рыба», то могут получиться суждения: «Все караси являются рыбами», «Некоторые рыбы являются карасями».
2. Любое суждение выражается в форме предложения (вспомним, понятие выражается словом или словосочетанием). Однако не всякое предложение может выражать суждение. Как известно, предложения бывают повествовательными, вопросительными и восклицательными. В вопросительных и восклицательных предложениях ничего не утверждается и не отрицается, поэтому они не могут выражать собой суждение. Повествовательное предложение, наоборот, всегда что-либо утверждает или отрицает, в силу чего суждение выражается в форме повествовательного предложения. Тем не менее есть такие вопросительные и восклицательные предложения, которые только по форме являются вопросами и восклицаниями, а по смыслу что-то утверждают или отрицают. Они называются риторическими. Например, известное высказывание: «И какой же русский не любит быстрой езды?» – представляет собой риторическое вопросительное предложение (риторический вопрос), т. к. в нём в форме вопроса утверждается, что всякий русский любит быструю езду.
В подобном вопросе заключено суждение. То же самое можно сказать о риторических восклицаниях. Например, в высказывании: «Попробуй найти чёрную кошку в тёмной комнате, если её там нет!» – в форме восклицательного предложения утверждается мысль о невозможности предложенного действия, в силу чего данное восклицание выражает собой суждение. Понятно, что не риторический, а настоящий вопрос, например: «Как тебя зовут?» – не выражает суждение, точно так же, как не выражает его настоящее, а не риторическое восклицание, например: «Прощай, свободная стихия!».
3. Любое суждение является истинным или ложным. Если суждение соответствует действительности, оно истинное, а если не соответствует – ложное. Например, суждение: «Все розы – это цветы», – является истинным, а суждение: «Все мухи – это птицы», – ложным. Надо отметить, что понятия, в отличие от суждений, не могут быть истинными или ложными. Невозможно, например, утверждать, что понятие «школа» – истинное, а понятие «институт» – ложное, понятие «звезда» – истинное, а понятие «планета» – ложное и т. п. Но разве понятия «Змей Горыныч», «Кощей Бессмертный», «вечный двигатель» не ложные? Нет, эти понятия являются нулевыми (пустыми), но не истинными и не ложными. Вспомним, понятие – это форма мышления, которая обозначает какой-либо объект, – и именно поэтому не может быть истинным или ложным. Истинность или ложность – это всегда характеристика какого-то высказывания, утверждения или отрицания, поэтому она применима только к суждениям, но не к понятиям. Поскольку любое суждение принимает одно из двух значений – истины или лжи – то аристотелевская логика также часто называется двузначной логикой.
4. Суждения бывают простыми и сложными. Сложные суждения состоят из простых, соединённых каким-либо союзом.
Как видим, суждение – это более сложная форма мышления по сравнению с понятием. Неудивительно поэтому, что суждение имеет определённую структуру, в которой можно выделить четыре части:
1. Субъект (обозначается латинской буквой S) – это то, о чём идёт речь в суждении. Например, в суждении: «Все учебники являются книгами», – речь идёт об учебниках, поэтому субъектом данного суждения выступает понятие «учебники».
2. Предикат (обозначается латинской буквой Р) – это то, что говорится о субъекте. Например, в том же суждении: «Все учебники являются книгами», – о субъекте (об учебниках) говорится, что они – книги, поэтому предикатом данного суждения выступает понятие «книги».
3. Связка – это то, что соединяет субъект и предикат. В роли связки могут быть слова «есть», «является», «это» и т. п.
4. Квантор – это указатель на объём субъекта. В роли квантора могут быть слова «все», «некоторые», «ни один» и т. п.
Рассмотрим суждение: «Некоторые люди являются спортсменами». В нём субъектом выступает понятие «люди», предикатом – понятие «спортсмены», роль связки играет слово «являются», а слово «некоторые» представляет собой квантор. Если в каком-то суждении отсутствует связка или квантор, то они всё равно подразумеваются. Например, в суждении: «Тигры – это хищники», – квантор отсутствует, но он подразумевается – это слово «все». С помощью условных обозначений субъекта и предиката можно отбросить содержание суждения и оставить только его логическую форму.
Например, если у суждения: «Все прямоугольники – это геометрические фигуры», – отбросить содержание и оставить форму, то получится: «Все S есть Р». Логическая форма суждения: «Некоторые животные не являются млекопитающими», – «Некоторые S не есть Р».
Субъект и предикат любого суждения всегда представляют собой какие-либо понятия, которые, как мы уже знаем, могут находиться в различных отношениях между собой. Между субъектом и предикатом суждения могут быть следующие отношения.
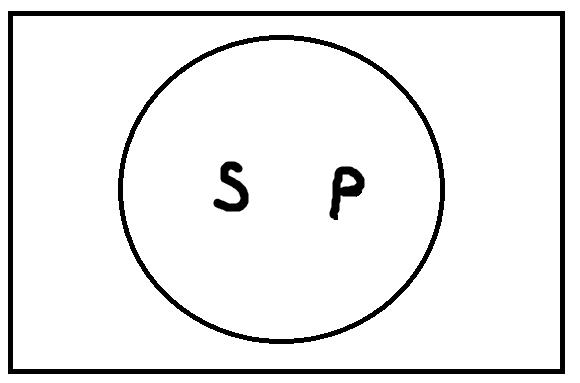
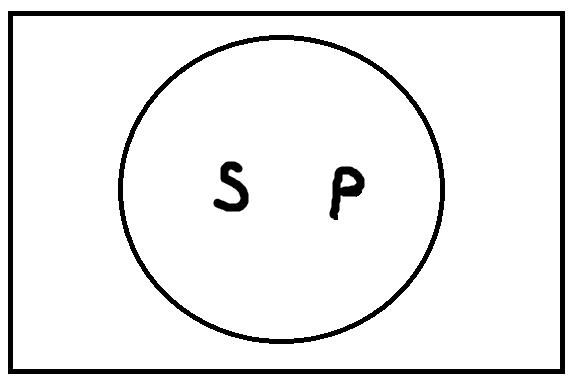
1. Равнозначность. В суждении: «Все квадраты – это равносторонние прямоугольники», – субъект «квадраты» и предикат «равносторонние прямоугольники» находятся в отношении равнозначности, потому что представляют собой равнозначные понятия (квадрат – это обязательно равносторонний прямоугольник, S = P а равносторонний прямоугольник – это обязательно квадрат) (рис. 18).
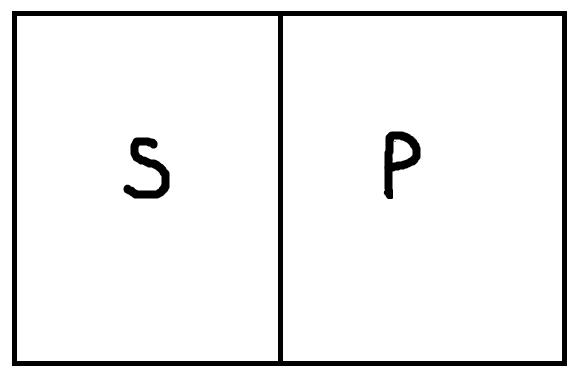
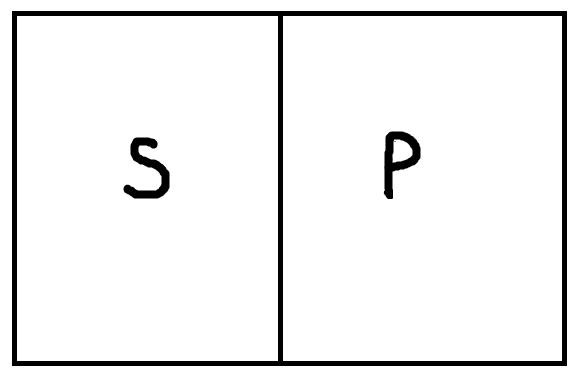
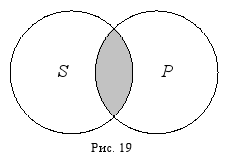
2. Пересечение. В суждении:
«Некоторые писатели – это американцы», – субъект «писатели» и предикат «американцы» находятся в отношении пересечения, т. к. являются пересекающимися понятиями (писатель может быть американцем и может им не быть, и американец может быть писателем, но также может им не быть) (рис. 19).
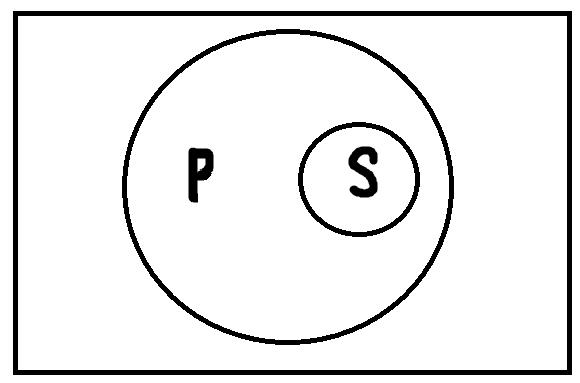
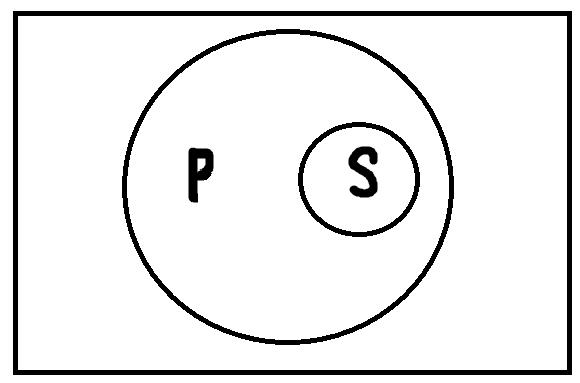
3. Подчинение. В суждении:
«Все тигры – это хищники», – субъект «тигры» и предикат «хищники» находятся в отношении подчинения, потому что представляют собой видовое и родовое понятия (тигр – это обязательно хищник, но хищник не обязательно тигр). Так же в суждении: «Некоторые хищники являются тиграми», – субъект «хищники» и предикат «тигры» находятся в отношении подчинения, будучи родовым и видовым понятиями. Итак, в случае подчинения между субъектом и предикатом суждения возможны два варианта отношений: объём субъекта полностью включается в объём предиката (рис. 20, a), или наоборот (рис. 20, б).
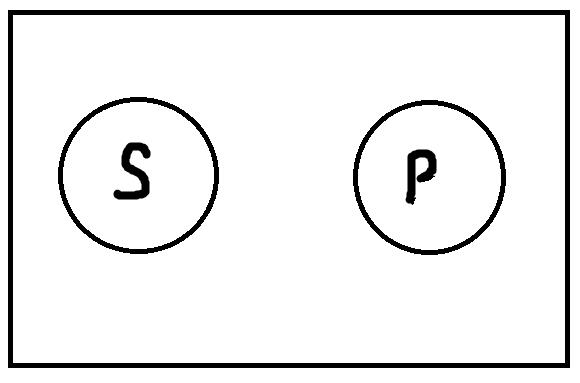
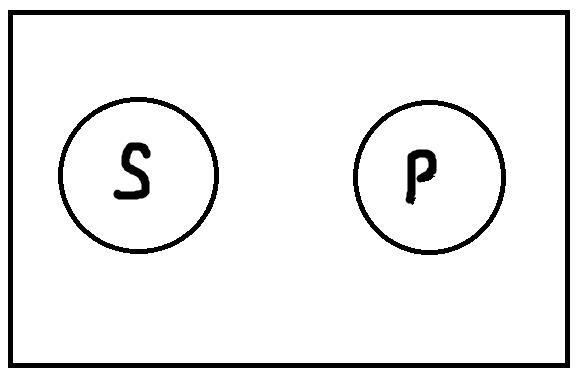
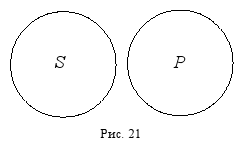
4. Несовместимость. В суждении: «Все планеты не являются звёздами», – субъект «планеты» и предикат «звёзды» находятся в отношении несовместимости, т. к. являются несовместимыми (соподчинёнными) понятиями (ни одна планета не может быть звездой, и ни одна звезда не может быть планетой) (рис. 21).
Чтобы установить, в каком отношении находятся субъект и предикат того или иного суждения, надо сначала установить, какое понятие данного суждения является субъектом, а какое – предикатом. Например, надо определить отношение между субъектом и предикатом в суждении: «Некоторые военнослужащие являются россиянами». Сначала находим субъект суждения, – это понятие «военнослужащие»; затем устанавливаем его предикат, – это понятие «россияне». Понятия «военнослужащие» и «россияне» находятся в отношении пересечения (военнослужащий может быть россиянином и может им не быть, и россиянин может как быть, так и не быть военнослужащим). Следовательно, в указанном суждении субъект и предикат пересекаются. Точно так же в суждении: «Все планеты – это небесные тела», – субъект и предикат находятся в отношении подчинения, а в суждении: «Ни один кит не является рыбой», – субъект и предикат несовместимы.
Как правило, все суждения подразделяют на три вида:
1. Атрибутивные суждения (от лат. attributum – атрибут) – это суждения, в которых предикат представляет собой какой-либо существенный, неотъемлемый признак субъекта. Например, суждение: «Все воробьи – это птицы», – атрибутивное, потому что его предикат является неотъемлемым признаком субъекта: быть птицей – это главный признак воробья, его атрибут, без которого он не будет самим собой (если некий объект не птица, то он обязательно и не воробей). Надо отметить, что в атрибутивном суждении не обязательно предикат является атрибутом субъекта, может быть и наоборот – субъект представляет собой атрибут предиката. Например, в суждении: «Некоторые птицы – это воробьи» (как видим, по сравнению с вышеприведённым примером, субъект и предикат поменялись местами), субъект является неотъемлемым признаком (атрибутом) предиката. Однако эти суждения всегда можно формально изменить таким образом, что предикат станет атрибутом субъекта. Поэтому атрибутивными обычно называются те суждения, в которых предикат является атрибутом субъекта.
2. Экзистенциальные суждения (от лат. existentia – существование) – это суждения, в которых предикат указывает на существование или несуществование субъекта. Например, суждение: «Вечных двигателей не бывает», – является экзистенциальным, т. к. его предикат «не бывает» свидетельствует о несуществовании субъекта (вернее –предмета, который обозначен субъектом).
3. Релятивные суждения (от лат. relativus – относительный) – это суждения, в которых предикат выражает собой какое-то отношение к субъекту. Например, суждение: «Москва основана раньше Санкт-Петербурга»,– является релятивным, потому что его предикат «основана раньше Санкт-Петербурга» указывает на временное (возрастное) отношение одного города и соответствующего понятия к другому городу и соответствующему понятию, представляющему собой субъект суждения.
1. Что такое суждение? Каковы его основные свойства и отличия от понятия?
2. В каких языковых формах выражается суждение? Почему вопросительные и восклицательные предложения не могут выражать собой суждения? Что такое риторические вопросы и риторические восклицания? Могут ли они быть формой выражения суждений?
3. Найдите в приведённых ниже выражениях языковые формы суждений:
1) Неужели ты не знал, что Земля вращается вокруг Солнца?
2) Прощай, немытая Россия!
3) Кто написал философский трактат «Критика чистого разума»?
4) Логика появилась примерно в V в. до н. э. в Древней Греции.
5) Первый президент Америки.
6) Разворачивайтесь в марше!
7) Мы все учились понемногу…
8) Попробуй-ка двигаться со скоростью света!
4. Почему понятия в отличие от суждений не могут быть истинными или ложными? Что такое двузначная логика?
5. Какова структура суждения? Придумайте пять суждений и укажите в каждом из них субъект, предикат, связку и квантор.
6. В каких отношениях могут быть субъект и предикат суждения? Приведите по три примера для каждого случая отношений между субъектом и предикатом: равнозначности, пересечения, подчинения, несовместимости.
7. Определите отношения между субъектом и предикатом и изобразите их с помощью круговых схем Эйлера для следующих суждений:
1) Все бактерии являются живыми организмами.
2) Некоторые русские писатели – это всемирно известные люди.
3) Учебники не могут быть развлекательными книгами.
4) Антарктида представляет собой ледовый материк.
8. Что такое атрибутивные, экзистенциальные и релятивные суждения? Приведите, самостоятельно подобрав, по пять примеров для атрибутивных, экзистенциальных и релятивных суждений.
2.2. Простые суждения
Если в суждении присутствуют один субъект и один предикат, то оно является простым. Все простые суждения по объёму субъекта и качеству связки делятся на четыре вида. Объём субъекта может быть общим («все») и частным («некоторые»), а связка может быть утвердительной («есть») и отрицательной («не есть»):
Объём субъекта ……………… «все» «некоторые»
Качество связки ……………… «есть» «не есть»
Как видим, на основе объёма субъекта и качества связки можно выделить только четыре комбинации, которыми исчерпываются все виды простых суждений: «все – есть», «некоторые – есть», «все – не есть», «некоторые – не есть». Каждый из этих видов имеет своё название и условное обозначение:
1. Общеутвердительные суждения (обозначаются латинской буквой A) – это суждения с общим объёмом субъекта и утвердительной связкой: «Все S есть Р». Например: «Все школьники являются учащимися».
2. Частноутвердительные суждения (обозначаются латинской буквой I) – это суждения с частным объёмом субъекта и утвердительной связкой: «Некоторые S есть Р». Например: «Некоторые животные являются хищниками».
3. Общеотрицательные суждения (обозначаются латинской буквой E) – это суждения с общим объёмом субъекта и отрицательной связкой: «Все S не есть Р (или «Ни одно S не есть Р»). Например: «Все планеты не являются звёздами», «Ни одна планета не является звездой».
Далее следует ответить на вопрос, к каким суждениям – общим или частным – следует относить суждения с единичным объёмом субъекта (т. е. те суждения, в которых субъект представляет собой единичное понятие), например: «Солнце – это небесное тело», «Москва основана в 1147 г.», «Антарктида – это один из материков Земли». Суждение является общим, если речь в нём идёт обо всём объёме субъекта, и частным, если речь идёт о части объёма субъекта. В суждениях с единичным объёмом субъекта речь идёт обо всём объёме субъекта (в приведённых примерах – обо всём Солнце, обо всей Москве, обо всей Антарктиде). Таким образом, суждения, в которых субъект является единичным понятием, считаются общими (общеутвердительными или общеотрицательными). Так, три приведённых выше суждения – общеутвердительные, а суждение: «Известный итальянский учёный эпохи Возрождения Галилео Галилей не является автором теории электромагнитного поля», – общеотрицательное.
В дальнейшем будем говорить о видах простых суждений, не употребляя их длинных названий, с помощью условных обозначений – латинских букв A, I, E, O. Эти буквы, взятые из двух латинских слов: affirmo – утверждать и nego – отрицать, были предложены в качестве обозначения видов простых суждений ещё в Средние века.
Важно отметить, что в каждом из видов простых суждений субъект и предикат находятся в определённых отношениях. Так, общий объём субъекта и утвердительная связка суждений вида A приводят к тому, что в них субъект и предикат могут быть в отношениях равнозначности или подчинения (других отношений между субъектом и предикатом в суждениях вида A быть не может). Например, в суждении: «Все квадраты (S) – это равносторонние прямоугольники (Р)», – субъект и предикат находятся в отношении равнозначности, а в суждении: «Все киты (S) – это млекопитающие животные (Р)», – в отношении подчинения.
Частный объём субъекта и утвердительная связка суждений вида I обусловливают то, что в них субъект и предикат могут быть в отношениях пересечения или подчинения (но не в других). Например, в суждении: «Некоторые спортсмены (S) – это негры (Р)», – субъект и предикат находятся в отношении пересечения, а в суждении: «Некоторые деревья (S) – это сосны (Р)», – в отношении подчинения.
Общий объём субъекта и отрицательная связка суждений вида E приводят к тому, что в них субъект и предикат находятся только в отношении несовместимости. Например, в суждениях: «Все киты (S) – это не рыбы (Р)», «Все планеты (S) не являются звёздами (Р)», «Все треугольники (S) – это не квадраты (Р)», – субъект и предикат несовместимы.
Частный объём субъекта и отрицательная связка суждений вида O обусловливают то, что в них субъект и предикат, так же как и в суждениях вида I, могут быть только в отношениях пересечения и подчинения. Читатель без труда сможет подобрать примеры суждений вида O, в которых субъект и предикат находятся в этих отношениях.
1. Что такое простое суждение?
2. На каком основании простые суждения подразделяются на виды? Почему они делятся именно на четыре вида?
3. Охарактеризуйте все виды простых суждений: название, структура, условное обозначение. Придумайте пример для каждого из них. К каким суждениям – общим или частным – относятся суждения с единичным объёмом субъекта?
4. Откуда взяты буквы для обозначения видов простых суждений?
5. В каких отношениях могут быть субъект и предикат в каждом из видов простых суждений? Подумайте, почему в суждениях вида A субъект и предикат не могут пересекаться или быть несовместимыми? Почему в суждениях вида I субъект и предикат не могут находиться в отношениях равнозначности или несовместимости? Почему в суждениях вида E субъект и предикат не могут быть равнозначными, пересекающимися или подчинёнными? Почему в суждениях вида O субъект и предикат не могут находиться в отношении равнозначности или несовместимости? Изобразите кругами Эйлера возможные отношения между субъектом и предикатом во всех видах простых суждений.
2.3. Распределённые и нераспределённые термины
Терминами суждения называются его субъект и предикат.
Термин считается распределённым (развёрнутым, исчерпанным, взятым в полном объёме), если в суждении речь идёт обо всех объектах, входящих в объём этого термина. Распределённый термин обозначается знаком «+», а на схемах Эйлера изображается полным кругом (кругом, который не содержит в себе другого круга и не пересекается с другим кругом) (рис. 22).
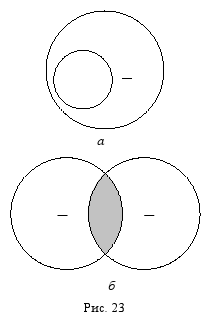
Термин считается нераспределённым (неразвёрнутым, неисчерпанным, взятым не в полном объёме), если в суждении речь идёт не обо всех объектах, входящих в объём этого термина. Нераспределённый термин обозначается знаком «–», а на схемах Эйлера изображается неполным кругом (кругом, который содержит в себе другой круг (рис. 23, a) или пересекается с другим кругом (рис. 23, б).
Например, в суждении: «Все акулы (S) являются хищниками (Р)», – речь идёт обо всех акулах, значит, субъект этого суждения распределён.
Однако в данном суждении речь идёт не обо всех хищниках, а только о части хищников (именно о тех, которые являются акулами), следовательно, предикат указанного суждения нераспределён. Изобразив отношения между субъектом и предикатом (которые находятся в отношении подчинения) рассмотренного суждения схемами Эйлера, увидим, что распределённому термину (субъекту «акулы») соответствует полный круг, а нераспределённому (предикату «хищники») – неполный (попадающий в него круг субъекта как бы вырезает из него какую-то часть):
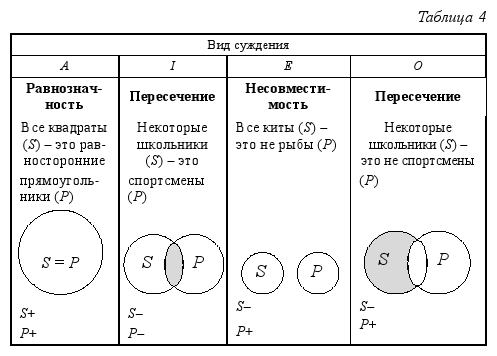
Распределённость терминов в простых суждениях может быть различной в зависимости от вида суждения и характера отношений между его субъектом и предикатом. В табл. 4 представлены все случаи распределённости терминов в простых суждениях:
Здесь рассмотрены все четыре вида простых суждений и все возможные случаи отношений между субъектом и предикатом в них (см. раздел 2. 2). Обратите внимание на суждения вида O, в котором субъект и предикат находятся в отношении пересечения. Несмотря на пересекающиеся круги на схеме Эйлера, субъект данного суждения нераспределён, а предикат распределён. Почему так получается? Выше мы говорили о том, что пересекающиеся на схеме круги Эйлера обозначают нераспределённые термины. Штриховкой показана та часть субъекта, о которой идёт речь в суждении (в данном случае – о школьниках, которые спортсменами не являются), в силу чего круг, обозначающий на схеме Эйлера предикат, остался полным (круг, обозначающий субъект, не отрезает от него какую-то часть, как это происходит в суждении вида I, где субъект и предикат находятся в отношении пересечения).
Итак, мы видим, что субъект всегда распределён в суждениях вида A и E и всегда не распределён в суждениях вида I и O, а предикат всегда распределён в суждениях вида E и O, но в суждениях вида A и I он может быть как распределённым, так и нераспределённым в зависимости от характера отношений между ним и субъектом в этих суждениях.
Проще всего устанавливать распределённость терминов в простых суждениях с помощью схем Эйлера (все случаи распределённости из таблицы запоминать совсем не обязательно). Достаточно уметь определять вид отношений между субъектом и предикатом в предложенном суждении и изображать их круговыми схемами. Далее ещё проще – полный круг, как уже говорилось, соответствует распределённому термину, а неполный – нераспределённому. Например, требуется установить распределённость терминов в суждении: «Некоторые русские писатели – это всемирно известные люди». Сначала найдём в этом суждении субъект и предикат: «русские писатели» – субъект, «всемирно известные люди» – предикат. Теперь установим, в каком они отношении. Русский писатель может как быть, так и не быть всемирно известным человеком, и всемирно известный человек может как быть, так и не быть русским писателем, следовательно, субъект и предикат указанного суждения находятся в отношении пересечения. Изобразим это отношение на схеме Эйлера, заштриховав ту часть, о которой идёт речь в суждении (рис. 25):
И субъект, и предикат изображаются неполными кругами (у каждого из них как бы отрезана какая-то часть), следовательно, оба термина предложенного суждения нераспределены (S –, P –).
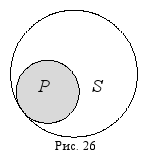
Рассмотрим ещё один пример. Надо установить распределённость терминов в суждении: «Некоторые люди – это спортсмены». Найдя в этом суждении субъект и предикат: «люди» – субъект, «спортсмены» – предикат, и установив отношение между ними – подчинение, изобразим его на схеме Эйлера, заштриховав ту часть, о которой идёт речь в суждении (рис. 26):
Круг, обозначающий предикат, является полным, а круг, соответствующий субъекту, – неполным (круг предиката как бы вырезает из него какую-то часть). Таким образом, в данном суждении субъект нераспределён, а предикат распределён (S –, P –).
1. В каком случае термин суждения считается распределённым, а в каком – нераспределённым? Как с помощью круговых схем Эйлера можно установить распределённость терминов в простом суждении?
2. Какова распределённость терминов во всех видах простых суждений и во всех случаях отношений между их субъектом и предикатом?
3. С помощью схем Эйлера установите распределённость терминов в следующих суждениях:
1) Все насекомые являются живыми организмами.
2) Некоторые книги – это учебники.
3) Некоторые учащиеся не являются успевающими.
4) Все города – это населённые пункты.
5) Ни одна рыба не является млекопитающим.
6) Некоторые древние греки являются знаменитыми учёными.
7) Некоторые небесные тела – это звёзды.
8) Все ромбы с прямыми углами – это квадраты.
2.4. Преобразование простого суждения
Существует три способа преобразования, т. е. изменения формы, простых суждений: обращение, превращение и противопоставление предикату.
Обращение (конверсия) – это преобразование простого суждения, при котором субъект и предикат меняются местами. Например, суждение: «Все акулы являются рыбами», – преобразуется путём обращения в суждение: «Некоторые рыбы являются акулами». Здесь может возникнуть вопрос, почему исходное суждение начинается с квантора «все», а новое – с квантора «некоторые»? Этот вопрос, на первый взгляд, кажется странным, ведь нельзя же сказать: «Все рыбы являются акулами», – следовательно, единственное, что остаётся, это: «Некоторые рыбы являются акулами». Однако в данном случае, мы обратились к содержанию суждения и по смыслу поменяли квантор «все» на квантор «некоторые»; а логика, как уже говорилось, отвлекается от содержания мышления и занимается только его формой. Поэтому обращение суждения: «Все акулы являются рыбами», – можно выполнить формально, не обращаясь к его содержанию (смыслу). Для этого установим распределённость терминов в этом суждении с помощью круговой схемы. Термины суждения, т. е. субъект «акулы» и предикат «рыбы», находятся в данном случае в отношении подчинения (рис. 27):
На круговой схеме видно, что субъект распределён (полный круг), а предикат нераспределён (неполный круг). Вспомнив, что термин распределён, когда речь идёт обо всех входящих в него предметах, и нераспределён, когда – не обо всех, мы автоматически мысленно ставим перед термином «акулы» квантор «все», а перед термином «рыбы» квантор «некоторые». Делая обращение указанного суждения, т. е. меняя местами его субъект и предикат и начиная новое суждение с термина «рыбы», мы опять же автоматически снабжаем его квантором «некоторые», не задумываясь о содержании исходного и нового суждений, и получаем безошибочный вариант: «Некоторые рыбы являются акулами». Возможно, всё это покажется чрезмерным усложнением элементарной операции, однако, как увидим далее, в иных случаях преобразование суждений сделать непросто без использования распределённости терминов и круговых схем.
Обратим внимание на то, что в рассмотренном выше примере исходное суждение было вида A, а новое – вида I, т. е. операция обращения привела к смене вида простого суждения. При этом, конечно же, поменялась его форма, но не поменялось содержание, ведь в суждениях: «Все акулы являются рыбами» и «Некоторые рыбы являются акулами», – речь идёт об одном и том же. В табл. 5 представлены все случаи обращения в зависимости от вида простого суждения и характера отношений между его субъектом и предикатом:
Суждение вида A обращается или в само себя, или в суждение вида I. Суждение вида I обращается или в само себя, или в суждение вида A. Суждение вида E всегда обращается в само себя, а суждение вида O не поддаётся обращению.
Второй способ преобразования простых суждений, называемый превращением (обверсией), заключается в том, что у суждения меняется связка: положительная на отрицательную, или наоборот. При этом предикат суждения заменяется противоречащим понятием (т. е. перед предикатом ставится частица «не»). Например, то же самое суждение, которое мы рассматривали в качестве примера для обращения: «Все акулы являются рыбами», – преобразуется путём превращения в суждение: «Все акулы не являются не рыбами». Это суждение может показаться странным, ведь обычно так не говорят, хотя на самом деле перед нами более короткая формулировка той мысли, что ни одна акула не может быть таким существом, которое не является рыбой, или что множество всех акул исключается из множества всех существ, которые не являются рыбами. Субъект «акулы» и предикат «не рыбы» суждения, получившегося в результате превращения, находятся в отношении несовместимости.
Приведённый пример превращения демонстрирует важную логическую закономерность: любое утверждение равно двойному отрицанию, и наоборот. Как видим, исходное суждение вида A в результате превращения стало суждением вида E. В отличие от обращения превращение не зависит от характера отношений между субъектом и предикатом простого суждения. Поэтому суждение вида A всегда превращается в суждение вида E, а суждение вида E – в суждение вида A. Суждение вида I всегда превращается в суждение вида O, а суждение вида O – в суждение вида I (рис. 28).
Третий способ преобразования простых суждений – противопоставление предикату – состоит в том, что сначала суждение подвергается превращению, а потом обращению. Например, чтобы путём противопоставления предикату преобразовать суждение: «Все акулы являются рыбами», – надо сначала подвергнуть его превращению. Получится: «Все акулы не являются не рыбами». Теперь надо совершить обращение с получившимся суждением, т. е. поменять местами его субъект «акулы» и предикат «не рыбы». Чтобы не ошибиться, вновь прибегнем к установлению распределённости терминов с помощью круговой схемы (субъект и предикат в этом суждении находятся в отношении несовместимости) (рис. 29):
На круговой схеме видно, что и субъект, и предикат распределены (и тому, и другому термину соответствует полный круг), следовательно, мы должны сопроводить как субъект, так и предикат квантором «все». После этого совершим обращение с суждением: «Все акулы не являются не рыбами». Получится: «Все не рыбы не являются акулами». Суждение звучит непривычно, однако это – более короткая формулировка той мысли, что если какое-то существо не является рыбой, то оно никак не может быть акулой, или что все существа, которые не являются рыбами, автоматически не могут быть и акулами в том числе. Обращение можно было сделать и проще, посмотрев в табл. 5 для обращения, которая приведена выше. Увидев, что суждение вида E всегда обращается в само себя, мы могли, не используя круговой схемы и не устанавливая распределённости терминов, сразу поставить перед предикатом «не рыбы» квантор «все». В данном случае был предложен другой способ, чтобы показать, что вполне можно обойтись без табл. для обращения, и запоминать её совсем необязательно. Здесь происходит примерно то же самое, что и в математике: можно запоминать различные формулы, но можно обойтись и без запоминания, т. к. любую формулу нетрудно вывести самостоятельно.
Все три операции преобразования простых суждений проще всего совершать с помощью круговых схем. Для этого надо изобразить три термина: субъект, предикат и понятие, противоречащее предикату (непредикат). Потом следует установить их распределённость, и из получившейся схемы Эйлера будут вытекать четыре суждения – одно исходное и три результата преобразований. Главное, помнить, что распределённый термин соответствует квантору «все», а нераспределённый – квантору «некоторые»; что соприкасающиеся на схеме Эйлера круги соответствуют связке «является», а несоприкасающиеся – связке «не является». Например, требуется совершить три операции преобразования с суждением: «Все учебники являются книгами». Изобразим субъект «учебники», предикат «книги» и непредикат «не книги» круговой схемой и установим распределённость этих терминов (рис. 30):
Получившуюся круговую схему можно прочитать четырьмя способами:
1. Все учебники являются книгами (исходное суждение).
2. Некоторые книги являются учебниками (обращение).
3. Все учебники не являются не книгами (превращение).
4. Все не книги не являются учебниками (противопоставление предикату).
Рассмотрим ещё один пример. Надо преобразовать тремя способами суждение: «Все планеты не являются звёздами». Изобразим кругами Эйлера субъект «планеты», предикат «звёзды» и непредикат «не звёзды». Обратите внимание на то, что понятия «планеты» и «не звёзды» находятся в отношении подчинения: планета – это обязательно не звезда, но небесное тело, которое не является звездой – это не обязательно планета. Установим распределённость этих терминов (рис. 31):
Получившуюся круговую схему можно прочитать четырьмя разными способами:
1. Все планеты не являются звёздами (исходное суждение).
2. Все звёзды не являются планетами (обращение).
3. Все планеты являются не звёздами (превращение).
4. Некоторые не звёзды являются планетами (противопоставление предикату).
1. Каким образом осуществляется операция обращения? Возьмите три каких-нибудь суждения и произведите с каждым из них обращение. Как происходит обращение во всех видах простых суждений и во всех случаях отношений между их субъектом и предикатом? Какие суждения не поддаются обращению?
2. Что такое превращение? Возьмите три любых суждения и совершите с каждым из них операцию превращения.
3. Что представляет собой операция противопоставления предикату? Возьмите три каких-нибудь суждения и преобразуйте каждое из них путём противопоставления предикату.
4. Каким образом знания о распределённости терминов в простых суждениях и умение её устанавливать с помощью круговых схем может помочь в проведении операций преобразования суждений?
5. Возьмите какое-нибудь суждение вида A и совершите с ним все операции преобразования с помощью круговых схем и установления распределённости терминов. Сделайте то же самое с каким-нибудь суждением вида E.
2.5. Логический квадрат
Простые суждения делятся на сравнимые и несравнимые.
Сравнимые (идентичные по материалу) суждения имеют одинаковые субъекты и предикаты, но могут отличаться кванторами и связками. Например, суждения: «Все школьники изучают математику», «Некоторые школьники не изучают математику», – являются сравнимыми: у них совпадают субъекты и предикаты, а кванторы и связки различаются. Несравнимые суждения имеют разные субъекты и предикаты. Например, суждения: «Все школьники изучают математику», «Некоторые спортсмены – это олимпийские чемпионы», – являются несравнимыми: субъекты и предикаты у них не совпадают.
Сравнимые суждения бывают, как и понятия, совместимыми и несовместимыми и могут находиться в различных отношениях между собой.
Совместимыми называются суждения, которые могут быть одновременно истинными. Например, суждения: «Некоторые люди – это спортсмены», «Некоторые люди – это не спортсмены», – являются одновременно истинными и представляют собой совместимые суждения.
Несовместимыми называются суждения, которые не могут быть одновременно истинными: истинность одного из них обязательно означает ложность другого. Например, суждения: «Все школьники изучают математику», «Некоторые школьники не изучают математику», – не могут быть одновременно истинными и являются несовместимыми (истинность первого суждения с неизбежностью приводит к ложности второго).
Совместимые суждения могут находиться в следующих отношениях:
1. Равнозначность – это отношение между двумя суждениями, у которых и субъекты, и предикаты, и связки, и кванторы совпадают. Например, суждения: «Москва является древним городом»,
«Столица России является древним городом», – находятся в отношении равнозначности.
2. Подчинение – это отношение между двумя суждениями, у которых предикаты и связки совпадают, а субъекты находятся в отношении вида и рода. Например, суждения: «Все растения являются живыми организмами», «Все цветы (некоторые растения) являются живыми организмами», – находятся в отношении подчинения.
Несовместимые суждения могут находиться в следующих отношениях.
1. Противоположность (контрарность) – это отношение между двумя суждениями, у которых субъекты и предикаты совпадают, а связки различаются. Например, суждения: «Все люди являются правдивыми», «Все люди не являются правдивыми», – находятся в отношении противоположности. В этом отношении могут быть только общие суждения – общеутвердительные (A) и общеотрицательные (E). Важным признаком противоположных суждений является то, что они не могут быть одновременно истинными, но могут быть одновременно ложными. Так, два приведённых противоположных суждения не могут быть одновременно истинными, но могут быть одновременно ложными: неправда, что все люди являются правдивыми, но также неправда, что все люди не являются правдивыми.
Противоположные суждения могут быть одновременно ложными, потому что между ними, обозначающими какие-то крайние варианты, всегда есть третий, средний, промежуточный вариант. Если этот средний вариант будет истинным, то два крайних окажутся ложными. Между противоположными (крайними) суждениями: «Все люди являются правдивыми», «Все люди не являются правдивыми», – есть третий, средний вариант: «Некоторые люди являются правдивыми, а некоторые не являются таковыми», – который, будучи истинным суждением, обусловливает одновременную ложность двух крайних, противоположных суждений.
2. Противоречие (контрадикторность) – это отношение между двумя суждениями, у которых предикаты совпадают, связки различны, а субъекты отличаются своими объёмами, т. е. находятся в отношении подчинения (вида и рода). Например, суждения: «Все люди являются правдивыми», «Некоторые люди не являются правдивыми», – находятся в отношении противоречия. Важным признаком противоречащих суждений, в отличие от противоположных, является то, что между ними не может быть третьего, среднего, промежуточного варианта. В силу этого два противоречащих суждения не могут быть одновременно истинными и не могут быть одновременно ложными: истинность одного из них обязательно означает ложность другого, и наоборот – ложность одного обусловливает истинность другого. К противоположным и противоречащим суждениям мы ещё вернёмся, когда речь пойдёт о логических законах противоречия и исключённого третьего.
Рассмотренные отношения между простыми сравнимыми суждениями изображаются схематически с помощью логического квадрата (рис. 32), который был разработан ещё средневековыми логиками:
Вершины квадрата обозначают четыре вида простых суждений, а его стороны и диагонали – отношения между ними. Так, суждения вида A и вида I, а также суждения вида E и вида O находятся в отношении подчинения. Суждения вида A и вида E находятся в отношении противоположности, а суждения вида I и вида O – частичного совпадения. Суждения вида A и вида O, а также суждения вида E и вида I находятся в отношении противоречия. Неудивительно, что логический квадрат не изображает отношение равнозначности, потому что в этом отношении находятся одинаковые по виду суждения, т. е. равнозначность – это отношение между суждениями A и A, I и I, E и E, O и O. Чтобы установить отношение между двумя суждениями, достаточно определить, к какому виду относится каждое из них. Например, надо выяснить, в каком отношении находятся суждения: «Все люди изучали логику», «Некоторые люди не изучали логику». Видя, что первое суждение является общеутвердительным (A), а второе частноотрицательным (O), мы без труда устанавливаем отношение между ними с помощью логического квадрата – противоречие. Суждения: «Все люди изучали логику (A)», «Некоторые люди изучали логику (I)», находятся в отношении подчинения, а суждения: «Все люди изучали логику (A)», «Все люди не изучали логику (E)», – находятся в отношении противоположности.
Как уже говорилось, важным свойством суждений, в отличие от понятий, является то, что они могут быть истинными или ложными.
Что касается сравнимых суждений, то истинностные значения каждого из них определённым образом связаны с истинностными значениями остальных. Так, если суждение вида A является истинным или ложным, то три других (I, E, O), сравнимых с ним суждения (имеющих сходные с ним субъекты и предикаты), в зависимости от этого (от истинности или ложности суждения вида A) тоже являются истинными или ложными. Например, если суждение вида A: «Все тигры – это хищники», – является истинным, то суждение вида I: «Некоторые тигры – это хищники», – также является истинным (если все тигры – хищники, то и часть из них, т. е. некоторые тигры – это тоже хищники), суждение вида E: «Все тигры – это не хищники», – является ложным, и суждение вида O: «Некоторые тигры – это не хищники», – также является ложным. Таким образом, в данном случае из истинности суждения вида A вытекает истинность суждения вида I и ложность суждений вида E и вида O (разумеется, речь идёт о сравнимых суждениях, т. е. имеющих одинаковые субъекты и предикаты).
1. Какие суждения называются сравнимыми и какие – несравнимыми?
2. Что такое совместимые и несовместимые суждения? Приведите по три примера совместимых и несовместимых суждений.
3. В каких отношениях могут быть совместимые суждения? Приведите по два примера для отношений равнозначности, подчинения и частичного совпадения.
4. В каких отношениях могут быть несовместимые суждения?
Приведите по три примера для отношений противоположности и противоречия. Почему противоположные суждения могут быть одновременно ложными, а противоречащие не могут?
5. Что представляет собой логический квадрат? Каким образом он изображает отношения между суждениями? Почему логический квадрат не изображает отношение равнозначности? Как с помощью логического квадрата определять отношение между двумя простыми сравнимыми суждениями?
6. Возьмите какое-нибудь истинное или ложное суждения вида A и сделайте из него выводы об истинности сравнимых с ним суждений видов E, I, O. Возьмите какое-нибудь истинное или ложное суждения вида E и сделайте из него выводы об истинности сравнимых с ним суждений A, I, O.
2.6. Сложное суждение
В зависимости от союза, с помощью которого простые суждения соединяются в сложные, выделяется пять видов сложных суждений:
2. Дизъюнктивное суждение (дизъюнкция) – это сложное суждение с разделительным союзом «или». Вспомним, что, говоря о логических операциях сложения и умножения понятий, мы отмечали неоднозначность этого союза – он может использоваться как в нестрогом (неисключающем) значении, так и в строгом (исключающем). Неудивительно поэтому, что дизъюнктивные суждения делятся на два вида:
2. Строгая дизъюнкция – это сложное суждение с разделительным союзом «или» в его строгом (исключающем) значении, который обозначается условным знаком «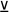
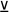
3. Импликативное суждение (импликация) – это сложное суждение с условным союзом «если … то», который обозначается условным знаком «>». С помощью этого знака импликативное суждение, состоящее из двух простых суждений, можно представить в виде формулы: a > b (читается «если a, то b»), где a и b – это два простых суждения. Например, сложное суждение: «Если вещество является металлом, то оно электропроводно», – представляет собой импликативное суждение (причинно-следственную связь) двух простых суждений: «Вещество является металлом», «Вещество электропроводно». В данном случае эти два суждения связаны таким образом, что из первого вытекает второе (если вещество – металл, то оно обязательно электропроводно), однако из второго не вытекает первое (если вещество электропроводно, то это вовсе не означает, что оно является металлом). Первая часть импликации называется основанием, а вторая – следствием; из основания вытекает следствие, но из следствия не вытекает основание. Формулу импликации: a > b, можно прочитать так: «если a, то обязательно b, но если b, то не обязательно a».
4. Эквивалентное суждение (эквиваленция) – это сложное суждение с союзом «если … то» не в его условном значении (как в случае с импликацией), а в тождественном (эквивалентном). В данном случае этот союз обозначается условным знаком «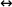
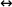
5. Отрицательное суждение (отрицание) – это сложное суждение с союзом «неверно, что…», который обозначается условным знаком «¬». С помощью этого знака отрицательное суждение можно представить в виде формулы: ¬a (читается «неверно, что a»), где a – это простое суждение. Здесь может возникнуть вопрос – где же вторая часть сложного суждения, которую мы обычно обозначали символом b? В записи: ¬a, уже присутствуют два простых суждения: a – это какое-то утверждение, а знак «¬» – его отрицание. Перед нами как бы два простых суждения – одно утвердительное, другое – отрицательное. Пример отрицательного суждения: «Неверно, что все мухи являются птицами».
Итак, мы рассмотрели пять видов сложных суждений: конъюнкцию, дизъюнкцию (нестрогую и строгую), импликацию, эквиваленцию и отрицание.
Союзов в естественном языке много, но все они по смыслу сводятся к рассмотренным пяти видам, и любое сложное суждение относится к одному из них. Например, сложное суждение: «Уж полночь близится, а Германа всё нет», – является конъюнкцией, потому что в нём союз «а» употребляется в роли соединительного союза «и». Сложное суждение, в котором вообще нет союза: «Посеешь ветер, пожнёшь бурю», – является импликацией, т. к. два простых суждения в нём связаны по смыслу условным союзом «если…то».
Любое сложное суждение является истинным или ложным в зависимости от истинности или ложности входящих в него простых суждений. Приведена табл. 6 истинности всех видов сложных суждений в зависимости от всех возможных наборов истинностных значений двух входящих в них простых суждений (таких наборов всего четыре): оба простых суждения истинные; первое суждение истинное, а второе ложное; первое суждение ложное, а второе истинное; оба суждения ложные).
Как видим, конъюнкция истинна только тогда, когда истинны оба входящих в неё простых суждения. Надо отметить, что конъюнкция, состоящая не из двух, а из большего числа простых суждений, также истинна только в том случае, когда истинны все входящие в неё суждения. Во всех остальных случаях она является ложной. Нестрогая дизъюнкция, наоборот, истинна во всех случаях за исключением того, когда оба входящих в неё простых суждения ложны. Нестрогая дизъюнкция, состоящая не из двух, а из большего числа простых суждений, также ложна только тогда, когда ложны все входящие в неё простые суждения. Строгая дизъюнкция истинна только тогда, когда одно входящее в неё простое суждение истинно, а другое ложно. Строгая дизъюнкция, состоящая не из двух, а из большего числа простых суждений, истинна только в том случае, если истинно только одно из входящих в неё простых суждений, а все остальные ложны. Импликация ложна только в одном случае – когда её основание является истинным, а следствие ложным. Во всех остальных случаях она истинна. Эквиваленция истинна тогда, когда два составляющих её простых суждения истинны или когда оба являются ложными. Если одна часть эквиваленции истинна, а другая ложна, то эквиваленция ложна. Проще всего определяется истинность отрицания: когда утверждение истинно, его отрицание ложно; когда утверждение ложно, его отрицание истинно.
1. На каком основании выделяются виды сложных суждений?
2. Охарактеризуйте все виды сложных суждений: название, союз, условное обозначение, формула, пример. Чем отличается нестрогая дизъюнкция от строгой? Как отличить импликацию от эквиваленции?
3. Каким образом можно определить вид сложного суждения, если в нём вместо союзов «и», «или», «если… то» употребляются какие-либо другие союзы?
4. Приведите по три примера для каждого вида сложных суждений, не используя при этом союзов «и», «или», «если…то».
5. Определите, к какому виду относятся следующие сложные суждения:
1. Живое существо является человеком только тогда, когда оно обладает мышлением.
2. Человечество может погибнуть то ли от истощения земных ресурсов, то ли от экологической катастрофы, то ли в результате третьей мировой войны.
3. Вчера он получил двойку не только по математике, но ещё и по русскому.
4. Проводник нагревается, когда через него проходит электрический ток.
5. Окружающий нас мир либо познаваем, либо нет.
6. Или же он совершенно бездарен, или же полный лентяй.
7. Когда человек льстит, он лжёт.
8. Вода превращается в лёд лишь при температуре от 0 °C и ниже.
6. От чего зависит истинность сложных суждений? Какие значения истинности принимают конъюнкция, нестрогая и строгая дизъюнкция, импликация, эквиваленция и отрицание в зависимости от всех наборов истинностных значений входящих в них простых суждений?
2.7. Логические формулы
Любое высказывание или целое рассуждение можно подвергнуть формализации. Это значит отбросить его содержание и оставить только его логическую форму, выразив её с помощью уже известных нам условных обозначений конъюнкции, нестрогой и строгой дизъюнкции, импликации, эквиваленции и отрицания.
Например, чтобы формализовать следующее высказывание: «Он занимается живописью, или музыкой, или литературой», – надо сначала выделить входящие в него простые суждения и установить вид логической связи между ними. В приведённое высказывание входят три простых суждения: «Он занимается живописью», «Он занимается музыкой», «Он занимается литературой».
Результатом формализации любого рассуждения, как мы увидели, является какая-либо формула, состоящая из маленьких букв латинского алфавита, выражающих входящие в рассуждение простые высказывания, и условных обозначений логических связей между ними (конъюнкции, дизъюнкции и др.). Все формулы делятся в логике на три вида:
1. Тождественно-истинные формулы являются истинными при всех наборах истинностных значений входящих в них переменных (простых суждений). Любая тождественно-истинная формула представляет собой логический закон.
2. Тождественно-ложные формулы являются ложными при всех наборах истинностных значений входящих в них переменных.
Тождественно-ложные формулы представляют собой отрицание тождественно-истинных формул и являются нарушением логических законов.
3. Выполнимые (нейтральные) формулы при различных наборах истинностных значений входящих в них переменных являются то истинными, то ложными.
Если в результате формализации какого-либо рассуждения получается тождественно-истинная формула, то такое рассуждение является логически безупречным. Если же результатом формализации будет тождественно-ложная формула, то рассуждение следует признать логически неверным (ошибочным). Выполнимая (нейтральная) формула свидетельствует о логической корректности того рассуждения, формализацией которого она является.
В четырёх последних колонках таблицы представлены истинностные значения каждого из этих двучленных сложных суждений, образующих формулу. Сначала заполним третью колонку таблицы. Для этого нам надо вернуться к предыдущему параграфу, где была представлена таблица истинности сложных суждений (см. табл. 6), которая в данном случае будет для нас базисной (как таблица умножения в математике). В этой таблице мы видим, что строгая дизъюнкция ложна, когда обе её части истинны или обе ложны; когда же одна её часть истинна, а другая ложна, тогда строгая дизъюнкция истинна. Поэтому значения строгой дизъюнкции в заполняемой таблице (сверху вниз) таковы: «ложно», «истинно», «истинно», «ложно». Далее заполним четвёртую колонку таблицы: ¬ а: когда утверждение два раза истинно и два раза ложно, тогда отрицание ¬ а, наоборот, два раза ложно и два раза истинно. Пятая колонка – это конъюнкция. Зная истинностные значения строгой дизъюнкции и отрицания, мы можем установить истинностные значения конъюнкции, которая истинна только тогда, когда истинны все входящие в неё элементы. Строгая дизъюнкция и отрицание, образующие данную конъюнкцию, одновременно истинны только в одном случае, следовательно конъюнкция один раз принимает значение «истинно», а в остальных случаях – «ложно». Наконец, надо заполнить последнюю колонку: для импликации, которая и будет представлять истинностные значения всей формулы. Возвращаясь к базисной таблице истинности сложных суждений, вспомним, что импликация ложна только в одном случае: когда её основание истинно, а следствие ложно. Основанием нашей импликации является конъюнкция, представленная в пятой колонке таблицы, а следствием простое суждение (b), представленное во второй колонке. Некоторое неудобство в данном случае заключено в том, что слева направо следствие идёт раньше основания, однако мы всегда можем мысленно поменять их местами. В первом случае (первая строчка таблицы, не считая «шапки») основание импликации ложно, а следствие истинно, значит, импликация истинна. Во втором случае и основание, и следствие ложны, значит, импликация истинна. В третьем случае и основание, и следствие истинны, значит, импликация истинна. В четвёртом случае, как и во втором, и основание, и следствие ложны, значит, импликация истинна.
Рассматриваемая формула принимает значение «истинно» при всех наборах истинностных значений входящих в неё переменных, следовательно, она является тождественно-истинной, а рассуждение, формализацией которого она выступает, логически безупречно.
Четвёртая колонка – истинностные значения конъюнкции. Пятая, последняя колонка – истинностные значения всей формулы – итоговой импликации. Таким образом, мы разбили формулу на три составные части, представляющие собой двучленные сложные суждения:
Заполним последовательно три последних колонки таблицы по тому же принципу, что и в предыдущем примере, т. е. опираясь на базисную таблицу истинности сложных суждений (см. табл. 6).
Рассматриваемая формула принимает как значение «истинно», так и значение «ложно» при различных наборах истинностных значений входящих в неё переменных, следовательно, она является выполнимой (нейтральной), а рассуждение, формализацией которого она выступает, логически корректно, но небезупречно: при ином содержании рассуждения такая форма его построения могла бы привести к ошибке, например: «Если слово стоит в начале предложения, то оно пишется с большой буквы. Слово «Москва» всегда пишется с большой буквы. Следовательно, слово «Москва» всегда стоит в начале предложения».
1. Что такое формализация высказывания или рассуждения? Придумайте какое-нибудь рассуждение и совершите его формализацию.
2. Формализуйте следующие рассуждения:
1) Если какое-либо вещество является металлом, то оно электропроводно. Медь является металлом. Следовательно, медь электропроводна.
2) Известный английский философ Фрэнсис Бэкон жил в XVII в., или в XV в., или в XIII в. Фрэнсис Бэкон жил в XVII в. Следовательно, он не жил ни в XV в., ни в XIII в.
3) Если ты не упрям, то ты можешь изменить своё мнение. Если же ты можешь изменить своё мнение, то ты способен признать данное суждение ложным. Следовательно, если ты не упрям, то ты способен признать данное суждение ложным.
4) Если сумма внутренних углов геометрической фигуры равна 180°, то такая фигура является треугольником. Сумма внутренних углов данной геометрической фигуры не равна 180°. Следовательно, данная геометрическая фигура не является треугольником.
5) Леса бывают хвойными, или лиственными, или смешанными. Этот лес не лиственный и не хвойный. Следовательно, этот лес смешанный.
3. Что представляют собой тождественно-истинные тождественно-ложные и выполнимые формулы? Что можно сказать о рассуждении, если результатом его формализации является тождественно-истинная формула? Каким будет рассуждение, если его формализация выражается тождественно-ложной формулой? Каковы, с точки зрения логической верности, рассуждения, которые при формализации приводят к выполнимым формулам?
4. Каким образом можно определить вид той или иной формулы, выражающей собой результат формализации некого рассуждения?
По какому алгоритму строятся и заполняются таблицы истинности для логических формул? Придумайте какое-нибудь рассуждение, формализуйте его и с помощью таблицы истинности определите вид получившейся формулы.
2.8. Виды и правила вопроса
Вопрос весьма близок к суждению. Это проявляется в том, что любое суждение можно рассматривать как ответ на некий вопрос.
Поэтому вопрос можно характеризовать в качестве логической формы, как бы предшествующей суждению, представляющей собой своего рода «предсуждение». Таким образом, вопрос – это логическая форма (конструкция), которая направлена на получение ответа в виде некоторого суждения.
Вопросы делятся на исследовательские и информационные.
Исследовательские вопросы направлены на получение нового знания. Это вопросы, на которые пока нет ответов. Например, вопрос: «Как родилась Вселенная?» – является исследовательским.
Информационные вопросы имеют своей целью приобретение (передачу от одного лица другому) уже имеющихся знаний (информации). Например, вопрос: «Какова температура плавления свинца?» – является информационным.
Вопросы также делятся на категориальные и пропозициональные.
Категориальные (восполняющие, специальные) вопросы включают в себя вопросительные слова «кто», «что», «где», «когда», «почему», «как» и т. п., указывающие направление поиска ответов и, соответственно, категорию объектов, свойств или явлений, в которой следует искать нужные ответы.
Пропозициональные (от лат. propositio – суждение, предложение) (уточняющие, общие) вопросы, которые также часто называют, направлены на подтверждение или отрицание некой уже имеющейся информации. В этих вопросах ответ как бы уже заложен в виде готового суждения, которое надо лишь подтвердить или отвергнуть. Например, вопрос: «Кто создал периодическую систему химических элементов?» – является категориальным, а вопрос: «Полезно ли изучение математики?» – пропозициональным.
Понятно, что и исследовательские, и информационные вопросы могут быть как категориальными, так и пропозициональными. Можно было бы выразиться наоборот: и категориальные, и пропозициональные вопросы могут быть как исследовательскими, так и информационными. Например: «Как создать универсальное доказательство теоремы Ферма?» – исследовательский категориальный вопрос:
«Есть ли во Вселенной планеты, населённые, как и Земля, разумными существами?» – исследовательский пропозициональный вопрос:
Любой вопрос имеет определённую структуру, которая состоит из двух частей. Первая часть представляет собой некую информацию (выраженную, как правило, каким-нибудь суждением), а вторая часть указывает на её недостаточность и необходимость её дополнения каким-либо ответом. Первая часть, называется основной (базисной) (её также иногда называют предпосылкой вопроса), а вторая часть – искомой. Например, в информационном категориальном вопросе: «Когда была создана теория электромагнитного поля?» – основная (базисная) часть – это утвердительное суждение: «Была создана теория электромагнитного поля», – а искомая часть, представленная вопросительным словом «когда», указывает на недостаточность информации, содержащейся в базисной части вопроса, и требует её дополнения, которое следует искать в области (категории) временных явлений. В исследовательском пропозициональном вопросе: «Возможны ли полёты землян в другие галактики?», – основная (базисная) часть представлена суждением: «Возможны полёты землян в другие галактики», – а искомая часть, выраженная частицей «ли», указывает на необходимость подтверждения или отрицания этого суждения. В данном случае искомая часть вопроса свидетельствует не об отсутствии какой-то информации, содержащейся в его базисной части, а об отсутствии знания о её истинности или ложности и требует это знание получить.
Наиболее важное логическое требование к постановке вопроса заключается в том, чтобы его основная (базисная) часть была истинным суждением. В этом случае вопрос считается логически корректным. Если же основная часть вопроса представляет собой ложное суждение, то вопрос следует признать логически некорректным. Подобные вопросы не требуют ответа и подлежат отвержению.
Например, вопрос: «Когда было предпринято первое кругосветное путешествие?» – является логически корректным, поскольку его основная часть выражена истинным суждением: «В истории человечества имело место первое кругосветное путешествие». Вопрос: «В каком году знаменитый английский учёный Исаак Ньютон закончил работу над общей теорией относительности?» – логически некорректен, т. к. его основная часть представлена ложным суждением: «Автором общей теории относительности является знаменитый английский учёный Исаак Ньютон».
Итак, основная (базисная часть) вопроса должна быть истинной и не должна быть ложной. Однако существуют логически корректные вопросы, основные части которых являются ложными суждениями. Например, вопросы: «Возможно ли создание вечного двигателя?», «Есть ли разумная жизнь на Марсе?», «Изобретут ли машину времени?» – несомненно, следует признать логически корректными, несмотря на то, что их базисные части представляют собой ложные суждения: «Возможно создание вечного двигателя», «Есть разумная жизнь на Марсе», «Изобретут машину времени». Дело в том, что искомые части этих вопросов направлены на выяснение истинностных значений их основных, базисных частей, т. е. требуется выяснить, истинными или ложными являются суждения: «Возможно создание вечного двигателя», «Есть разумная жизнь на Марсе», «Изобретут машину времени». В этом случае вопросы логически корректны. Если бы искомые части рассматриваемых вопросов не были направлены на выяснение истинности их основных частей, а имели бы своей целью нечто иное, эти вопросы являлись бы логически некорректными, например: «Где был создан первый вечный двигатель?», «Когда появилась разумная жизнь на Марсе?», «Сколько будет стоить путешествие на машине времени?». Таким образом, главное правило постановки вопроса следует расширить и уточнить: основная (базисная) часть корректного вопроса должна быть истинным суждением; если же она является ложным суждением, то его искомая часть должна быть направлена на выяснение истинностного значения основной части; в противном случае вопрос будет логически некорректным. Нетрудно догадаться, что требование для основной части быть истинной, по преимуществу, относится к категориальным вопросам, а требование того, чтобы искомая часть была выяснением истинности основной части, относится к пропозициональным вопросам.
Надо отметить, что корректные категориальные и пропозициональные вопросы сходны между собой в том, что на них всегда можно дать истинный ответ (как, впрочем, и ложный). Например, на категориальный вопрос: «Когда закончилась первая мировая война?» – можно дать как истинный ответ: «В 1918 г.», – так и ложный: «В 1916 г.». На пропозициональный вопрос: «Вращается ли Земля вокруг Солнца?» – также можно дать как истинный: «Да, вращается», – так и ложный: «Нет, не вращается», – ответ. Оба приведённых вопроса логически корректны. Итак, принципиальная возможность получения истинных ответов есть основной признак корректных вопросов. Если же получить истинные ответы на некие вопросы принципиально невозможно, то они являются некорректными. Например, нельзя получить истинный ответ на пропозициональный вопрос: «Закончится ли когда-нибудь первая мировая война?» – так же, как невозможно получить его на категориальный вопрос: «С какой скоростью вращается Солнце вокруг неподвижной Земли?».
Любые ответы на эти вопросы необходимо будет признать неудовлетворительными, а сами вопросы – логически некорректными, подлежащими отвержению.
1. Что такое вопрос? В чём заключается близость вопроса и суждения?
2. Чем отличаются исследовательские вопросы от информационных? Приведите по пять примеров исследовательских и информационных вопросов.
3. Что представляют собой категориальные и пропозициональные вопросы? Приведите по пять примеров категориальных и пропозициональных вопросов.
4. Охарактеризуйте приведённые ниже вопросы с точки зрения их принадлежности к исследовательским или информационным, а также – категориальным или пропозициональным:
1) Когда был открыт закон всемирного тяготения?
2) Смогут ли жители Земли расселиться на других планетах Солнечной системы?
3) В каком году родился Бонапарт Наполеон?
4) Каково будущее человечества?
5) Возможно ли предотвратить третью мировую войну?
5. Какова логическая структура вопроса? Приведите пример категориального исследовательского вопроса и выделите в нём основную (базисную) и искомую части. Сделайте то же самое с категориальным информационным вопросом, пропозициональным исследовательским вопросом и пропозициональным информационным вопросом.
6. Какие вопросы являются логически корректными, а какие – некорректными? Приведите по пять примеров логически корректных и некорректных вопросов. Может ли быть у логически корректного вопроса ложная основная часть? Достаточно ли для определения корректного вопроса требования истинности его основной части?
Что объединяет логически корректные категориальные и пропозициональные вопросы?
7. Дайте ответ, какие из приведённых ниже вопросов являются логически корректными, а какие некорректными:
1) Во сколько раз планета Юпитер превосходит по размерам Солнце?
2) Какова площадь Тихого океана?
3) В каком году Владимир Владимирович Маяковский написал поэму «Облако в штанах»?
4) Как долго продолжалась плодотворная совместная научная работа Исаака Ньютона и Альберта Эйнштейна?
5) Чему равна длина экватора земного шара?