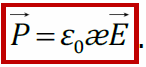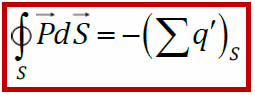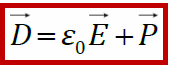Свободные и связанные электрические заряды, токи проводимости и смещения

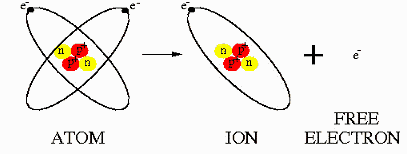
В зависимости от способности перемещаться в электрическом поле заряды могут быть разделены на две большие группы. Заряды первой группы характеризуются возможностью неограниченного перемещения в электрическом поле и поэтому называются свободными зарядами. Вторая группа зарядов не имеет этой возможности, их перемещение ограничивается структурой атома, молекулы, кристалла или неоднородностью строения вещества. Эти заряды называются связанными.

Разделение на свободные и связанные заряды не всегда зависит только от физической природы рассматриваемых частиц. Заряды, являющиеся свободными в однородной среде, могут оказаться связанными при образовании композиций, состоящих из различных материалов.

Свободные электроны и ионы вещества под действием электрического поля перемещаются от одного электрода к другому, образуя ток проводимости.

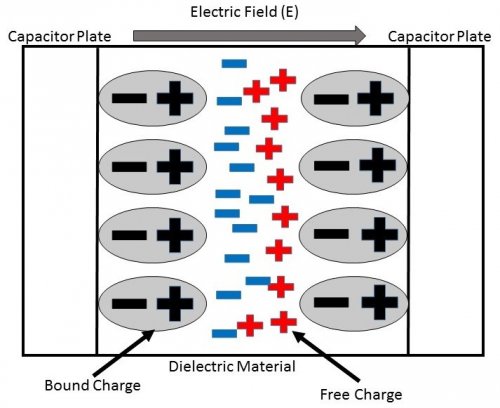
Связанные электрические заряды под действием электрического поля имеют возможность перемешаться только в некоторых, часто очень ограниченных, пределах. Этот процесс перемещения, называемый поляризацией, характеризуется вектором поляризации, и существенно зависит от физических связей между зарядами. При поляризации смещаются заряды под действием электрического поля и появляется ток смещения.

Диэлектрик содержит равное количество положительных и отрицательных связанных между собой зарядов, и влияние внешнего электрического поля сказывается на взаимном смещении центров положительных и отрицательных зарядов и в появлении электрических моментов пар разноименных зарядов — дипольных моментов. В однородном поле вектор поляризации представляет собой среднее значение суммарного дипольного момента единицы объема. Поляризации диэлектрика зависит от напряженности электрического поля.

Явление поляризации диэлектриков и появления тока смещения в промышленности используется при высокочастотном нагреве диэлектриков (например, сушка древесины, картона, нагрев в пищевой промышленности) и полупроводников.

Нагреваемый материал помещается между пластинами конденсатора, к которым подведено напряжение высокой частоты. Токи проводимости и смещения, возникающие в материале, помещенном в электрическом поле высокой частоты, вызывают выделение тепла в материале и его нагрев. Этот вид нагрева называется диэлектрическим нагревом.

Процесс сушки влажных материалов, т. е. удаление из них влаги, может происходить за счет двух явлений: непосредственного испарения влаги внутри материала и выхода ее в виде пара и перемещения влаги в жидкой фазе из внутренних областей к поверхности. Наличие электрического поля в материале оказывает существенное влияние на испарение и перемещение влаги, позволяя значительно интенсифицировать процесс сушки.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Источник

Типы поляризации диэлектрика

В отсутствие электрического поля

При наличии электрического поля

Электрическое поле в диэлектрике складывается из двух полей – поля свободных зарядов (внешнего электрического поля) и поля связанных зарядов:

Вектор поляризации (Поляризованность) P– векторная характеристика поляризации вещества, равная сумме дипольных моментов молекул вещества, занимающего единичный объём.

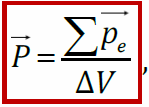
Дипольный момент молекулы параллелен и пропорционален напряжённости электрического поля:

где β – поляризуемостьмолекулы. здесь N – число молекул, n – концентрация. Обозначим – диэлектрическая восприимчивость вещества;

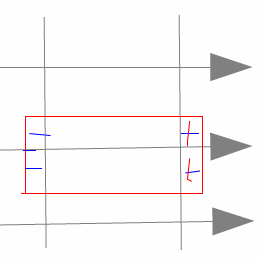
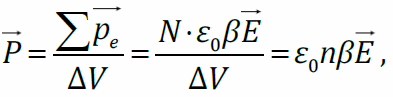
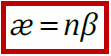
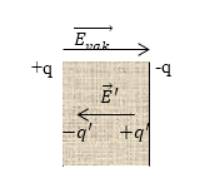
В поляризованном диэлектрике на его краях образуются связанные заряды. Каждый из связанных зарядов входит в состав диполя. σсв— поверхностная плотность связанных зарядов. Установим связь между поверхностной плотностью связанных зарядов (σсв) и вектором поляризации( ⃗P ). Вид сбоку на пластину диэлектрика. ⃗E⊥пластине

В общем случае σсв =Pn

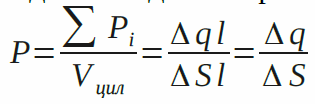
Поверхностная плотность связанных зарядов равна проекции вектора поляризации на

внешнюю нормаль (Pn) к поверхности диэлектрика.

Теорема Остроградского-Гаусса для вектора Р: поток поляризованности сквозь произвольную замкнутую поверхность равен сумме связанных зарядов, охваченной этой поверхностью, взятой с обратным знаком.

Сторонние и связанные заряды диэлектрика. Вывод теоремы Остроградского-Гаусса для поля в диэлектрике. Вектор электрического смещения н его связь с напряженностью поля. Диэлектрическая проницаемость вещества. Третье уравнение Максвелла.

Сторонние заряды – это заряды, расположенные за пределами диэлектрика, а также заряды, которые хотя и находятся в пределах диэлектрика, но не входят в состав его молекул.

Связанные заряды – это заряды, входящие в состав атомов и молекул диэлектрика. Под действием поля они могут лишь немного смещаться из своих положений равновесия. Плотность связанных зарядов равна по абсолютной величине проекции поляризованности на направление внешней нормали рассматриваемой поверхности

ТеоремаОстроградского-Гаусса утверждает: поток вектора напряженности электростатического поля через произвольную замкнутую поверхность прямо пропорционален алгебраической сумме свободных зарядов, расположенных внутри этой поверхности.

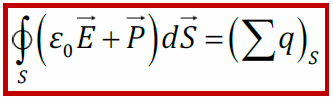
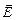
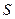
– электрическое смещение (электрическая индукция);

— теорема Остроградского-Гаусса для электрического смещения: поток вектора электрического смещения сквозь произвольную замкнутую поверхность равен сумме свободных зарядов, охваченных этой поверхностью.

D – это вспомогательная векторная характеристика электрического поля, помогающая расчёту E.Связь напряженности (Е) и вектора электрического смещения (D)

Где ε- Относительнаядиэлектри́ческаяпроница́емость среды.

Относительнаядиэлектри́ческаяпроница́емость среды — физическая величина, характеризующая свойства изолирующей (диэлектрической) среды и показывающая, во сколько раз сила взаимодействия двух электрических зарядов в этой среде меньше, чем в вакууме. Значение ε вакуума равно единице, для реальных сред ε > 1. Для воздуха и большинства других газов в нормальных условиях значение ε близко к единице в силу их низкой плотности. Электрическая постояннаяε₀ ≈ 8.85·10 −12 Ф/м

Третье уравнение Максвелла определяет источники электрического поля. Физический смысл этого уравнения состоит в том, что электрическое поле в некоторой области пространства связано с электрическим зарядом внутри этой поверхности.

Источник

Свободные и связанные заряды

Когда рассматриваются диэлектрики в электростатических полях, следует различать два вида электрических зарядов: свободные и связанные.

Свободные заряды – это заряды, перемещающиеся под действием поля на существенные расстояния.

Например, электроны в проводниках, ионы в газах и заряды, привносимые извне на поверхность диэлектриков, которые нарушают их (диэлектриков) нейтральность. Заряды, входящие в состав нейтральных, в целом, молекул диэлектриков, так же, как ионы, закрепленные в кристаллических решетках твердых диэлектриков около положений равновесия, получили название связанных зарядов.

Поверхностная плотность зарядов

Формула потенциала электростатического поля в диэлектрике φ запишется как:

Можно сделать вывод, что из ( 1 ) и ( 3 ) получим:

При использовании теоремы Остроградского-Гаусса с некоторыми формулами векторного анализа имеем совсем иной вид уравнения ( 4 ) :

Плотность связанных зарядов

Функция φ вида ( 7 ) будет решением уравнения:

Выражение ( 10 ) называют основным дифференциальным уравнением электростатического поля в любой произвольной среде.

Для получения полной системы уравнений электростатики, нужно использовать формулу ( 10 ) с определением, связывающим векторы напряженности электрического поля с векторами поляризации.

Зависимость P → E → представится как:

Если имеется внешнее электрическое поле, вещество становится источником поля, значит, поле изменяется.

Решение

Если при имеющихся обкладках конденсатора находится вакуум, то напряженность поля, создаваемого заряженными обкладками, запишется как:

Так как известна связь напряженности поля и вектора поляризации для изотропного диэлектрика, то

На основании выше сказанного зафиксируем, что напряженность поля в конденсаторе с диэлектриком запишется как:

Источник

Сторонние токи и заряды

При рассмотрении уравнений Максвелла (1.52) под вектором j подразумевалась плотность тока проводимости, возникающего в проводящей среде под воздействием электромагнитного поля. Этот вектор удовлетворяет закону Ома в дифференциальной форме (1.9). Для упрощения реальной электродинамической задачи обычно вместо имеющейся на самом деле системы рассматривают некоторую модель. При этом часть системы вообще исключается из рассмотрения. Для учета влияния этой части системы во многих случаях ее заменяют введением некоторых токов, которые рассматриваются как первопричина возникновения электромагнитного поля и считаются заданными. Эти токи принято называть сторонними. Например, при излучении электромагнитных волн элементарным электрическим вибратором ток в вибраторе обусловлен подведением к нему энергии от генератора. При анализе этот ток будет считаться известным, что позволит исключить из рассмотрения процессы, протекающие в генераторе, прохождение энергии по линии, соединяющей генератор с вибратором, и т.д., т.е. существенно упростит задачу. Если этого не делать и каждую проблему рас­сматривать во всей ее полноте, то любая конкретная задача становится трудноразрешимой.

Для учета сторонних токов следует первое уравнение Максвелла представить в виде:

(1.111)

где jст – плотность сторонних токов в рассматриваемой точке пространства, a j – как и прежде, плотность тока проводимости, вызванного электромагнитным полем: j = σE.

Аналогично сторонним токам вводится понятие сторонних зарядов. Они учитываются в третьем уравнении Максвелла:

div D = ρ + ρ ст, (1.112)

где ρст – объемная плотность сторонних зарядов.

Второе и четвертое уравнения Максвелла остаются без изменений. В случае переменных полей функции jст и ρст связаны уравнением непрерывности:

(1.113)

При анализе многих вопросов вместо сторонних токов за­даются сторонней напряженностью электрического поля Ест. В большинстве случаев при исследовании электродинамических яв­лений под Ест подразумевается напряженность электрического поля, создаваемого зарядами и токами, расположенными за пре­делами рассматриваемой области. При изучении постоянного электрического поля под Ест иногда понимают напряженность поля сторонних электродвижущих сил неэлектрического происхождения (химических, диффузионных и др.). Введение Ест является таким же упрощением задачи, как и введение jст. Фактически оно иск­лючает детальный анализ процессов, происходящих в какой-либо части пространства.

Выпишем также уравнения Максвелла для монохромати­ческого поля в однородной среде, учитывающие сторонние ис­точники:

, (1.114)

. (1.115)

Уравнение непрерывности для сторонних токов (1.113) в этом случае имеет вид:

. (1.116)

Третье уравнение Максвелла в комплексной форме

(1.117)

является следствием уравнений (1.114) и (1.116), а четвертое — следствием уравнения (1.115).

Систему уравнений Максвелла в комплексной форме (1.114)-(1.115) можно переписать также для комплексных амплитуд:

, (1.118)

. (1.119)

Источник

Электростатическое поле в диэлектриках. Связанные и сторонние заряды. Поляризация диэлектриков. Механизмы поляризации. Поляризационные заряды.

Диэлектрики –вещества,практически не проводящие эл. ток.

—Неполярные

—Полярные

—Ионные

Если в отсутствии внешнего электрического поля центры масс совпадают, то такие молекулы называются неполярными (неполярные диэлектрики).

Полярные молекулы обладают собственным дипольным моментом p(полярные диэлектрики).

Ионные диэлектрики представляют собой твердые неорганические диэлектрики с ионным типом химической связи.

В результате процесса поляризации в объеме (или на поверхности) диэлектрика возникают нескомпенсированные заряды, которые называются поляризационными, или связанными.

Частицы, обладающие этими зарядами, входят в состав молекул и под действием внешнего электрического поля смещаются из своих положений равновесия, не покидая молекулы, в состав которой они входят. Связанные заряды характеризуют поверхностной плотностью .

Поляризация диэлектриков — явление, связанное с ограниченным смещением связанных зарядов в диэлектрике или поворотом электрических диполей, обычно под воздействием внешнего электрического поля, иногда под действием других внешних сил или спонтанно.

Сторонние заряды –это заряды, не входящие в состав диэлектрика.

Типы поляризации:

— Электронная — смещение электронных оболочек атомов под действием внешнего электрического поля.

— Ионная — смещение узлов кристаллической решетки под действием внешнего электрического поля, причем смещение на величину, меньшую, чем величина постоянной решетки.

— Дипольная — протекает с потерями на преодоление сил связи и внутреннего трения. Связана с ориентацией диполей во внешнем электрическом поле.

Вектор поляризации — количественная мера поляризации диэлектрика, равная отношению суммарного дипольного момента физ. малого объема диэлектрика и этому объему :

Диэлектрическая восприимчивость (или поляризуемость) вещества — физическая величина, мера способности вещества поляризоваться под действием электрического поля.

где — электрическая постоянная, произведение называется в системе СИ абсолютной диэлектрической восприимчивостью.

Теорема Гаусса для поля вектора P:

Данное равенство должно выполняться для любого произвольно выбранного диэлектрика.

13. Вектор электрического смещения . Диэлектрическая проницаемость. Теорема Гаусса для поля вектора в интегральной и дифференциальной форме. Связь между и в изотропных диэлектриках.

— вектор электрического смещения или вектор индукции эл. поля или вектор

– Теорема Гаусса для поля вектора D в диф. форме —дивергенция векторного поля D в некот. точке равна объемной плотности стороннего заряда в этой точке.

Источником поля вектора D явл. только сторонние заряды.

– Теорема Гаусса для поля вектора D в инт. форме— поток вектора D индукции эл. поля через любую замкн.

поверхность (S) равен алгебраической сумме стор. зарядов, охватываемых этой поверхностью.

В случае изотропных диэлектриков:

Где диэлектрическая проницаемость в-ва.

14. Условия на границе раздела 2-х диэлектриков для векторов и . Закон преломления силовых линий. Физический смысл диэлектрической проницаемости среды.

Вблизи поверхности раздела 2-х изотропных диэлектриков при отс. сторонних зарядов поля векторов и удовлетворяют условиям:

; ; ; ;

На границе раздела 2-х диэлектриков:

— Тангенсальная составляющая:

— Нормальная составл. вектора:

Силов. линии поля векторов E,D на границе раздела 2-х сред испытывают разлом.

; ; ;

– законпреломления векторов

— модуль напряженности в диэлектрике
— модуль напряженности в вакууме
— диэлектрическая проницаемость среды

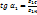
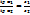
Физ. смысл : показывает, во сколько раз величина напряженности эл. поля

Источник