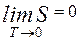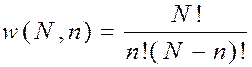что такое статистический вес или термодинамическая вероятность
СТАТИСТИЧЕСКИЙ ВЕС
Понятие «статистический вес» (используется также термин термодинамическая вероятность) является одним из основных в статистической физике. Чтобы сформулировать его определение необходимо сначала определить понятия макросостояние и микросостояние.
Одно и тоже состояние макроскопического тела можно охарактеризовать по-разному. Если состояние охарактеризовано заданием макроскопических параметров состояния (давление, объем, температура, плотность и т.п.) то такое состояние будем называть макросостоянием.
Если состояние охарактеризовано путем задания координат и скоростей всех молекул тела, то такое состояние будем называть микросостоянием.
Очевидно, что одно и то же макросостояние может быть реализовано различными способами, то есть различными микросостояниями. Число различных микросостояниий, которыми может быть реализовано данное макросостояние называется статистическим весом или термодинамической вероятностью.
Различные микросостояния отличаются при этом тем, какие именно молекулы находятся справа и слева. 1,2 – 3,4 (как показано на рисунке 9.5) одно из состояний. 1,3 – 2,4 – другое микросостояние.
Каждая из молекул может с равной вероятностью находиться и слева, и справа. Поэтому вероятность i-той молекуле находиться, например, справа равна ½. Появление в левой части сосуда 
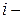
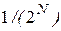
Утверждение о том, что, вероятности каждого их микросостояний равны, называются эргодической гипотезой, и оно лежит в основе статистической физики.
Рассмотрим N = 4. Каждое из размещений молекул в половинах сосуда является конкретным микросостоянием. Тогда макросостоянию с числом молекул слева 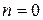
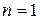
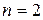
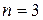
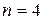
Теперь можно видеть, что вследствие принятия эргодической гипотезы, статистический вес оказывается пропорциональным вероятности (обычной!) реализации данного макросостояния.
Если в сосуде содержится N молекул, то можно доказать, что статвес макросостояния, заключающегося в том, что слева n молекул, а справа (N – n)
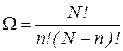
Если для четырех молекул вероятность собраться в одной из половин сосуда составляет 1/16, то есть вполне ощутимую величину, то уже для N = 24 эта вероятность составляет порядка 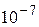
При нормальных условиях в 4 см 3 воздуха содержится около 10 20 молекул. Вероятность собраться им в одной из частей сосуда оценивается величиной 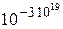
Таким образом, с увеличением количества молекул в системе вероятность существенных отклонений от приблизительного равенства количеств молекул в частях сосуда очень быстро убывает. Это соответствует тому, что статвес состояний с приблизительно равным количеством молекул в половинах оказывается очень большим и быстро убывает по мере отклонения от равенства молекул в частях.
Если число N не очень велико, то с течением времени наблюдаются – заметные отклонения количества молекул в одной из половины от N / 2. Случайные отклонения физической величиныx 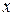
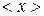
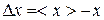
Среднее арифметическое абсолютной флуктуации 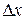
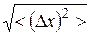
Более удобной и показательной является относительная флуктуация:
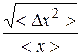
Причем в статистической физике доказывается соотношение:
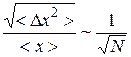
т.е. величина относительной флуктуации обратно пропорционально корню из количества частиц в системе. Это утверждение подтверждает наш качественный вывод.
Аналогично количеству молекул в одной из половин сосуда флуктуируют вблизи средних значений и другие макроскопические характеристики состояния – давление, плотность, и т.п.
Рассмотрим природу равновесных и неравновесных состояний и процессов с точки зрения статистической физики. Равновесным, по определению, является такое состояние, которое не имеет тенденции к изменению с течением времени. Ясно, что таким свойством в наибольшей мере будет обладать наиболее вероятное из всех макросостояний системы, то есть состояние, реализуемое наибольшим количеством микросостояний, а значит обладающее наибольшим статистическим весом. Поэтому равновесное состояние можно определить как состояние, статвес которого максимален.
Примером типичного необратимого процесса может служить распространение на весь объем сосуда молекул газа, первоначально сосредоточенных в одной из его половин. Этот процесс является необратимым, так как вероятность того, что в результате теплового движения все молекулы соберутся в одной из половин сосуда, очень мала. Соответственно всегда необратимым является процесс, обратный которому крайне маловероятен.


Как мы установили, вероятность состояния системы пропорциональна ее статическому весу, поэтому в качестве характеристики вероятности состояния можно было бы использовать сам статвес W. Однако W не является аддитивной величиной. Поэтому для характеристики состояния системы используют величину
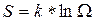
которую называют энтропией системы. Действительно, если мы рассмотрим две системы по 4 молекулы в каждой, то статистический вес состояния, когда в каждой из подсистем находится, например, по одной молекуле слева будет равен 16, т.е. 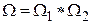
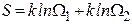
Поскольку при протекании необратимых процессов в изолированной системе она переходит из менее вероятных в более вероятные состояния, можно утверждать, что энтропия изолированной системы возрастает при протекании в ней необратимых процессов.
Равновесное состояние является наиболее вероятным состоянием, а значит, энтропия системы перешедшей в равновесное состояние максимальна.
Поэтому можно утверждать, что энтропия изолированной системы остается постоянной, если она находится в равновесном состоянии, или возрастает, если в ней протекают необратимые процессы.
Утверждение о том, что энтропия изолированной системы не убывает, называетсявторым началом термодинамики или законом возрастания энтропии.
Энтропия является, очевидно, функциейсостояния и должна определятся параметрами состояния. Самыми простыми свойствами обладает одноатомный идеальный газ – его состояния полностью определяется заданием двух параметров, например, температуры и объема. Соответственно его энтропию можно определить как функцию температуры и объема: 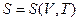
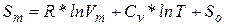
где 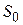
Теперь можно выяснить вопрос о том, как изменяется энтропия неизолированной системы, например при сообщении ей некоторого количества тепла 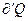
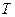
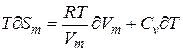
Но 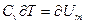
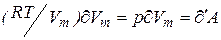
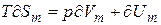
Входящие в (4) 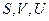

Согласно первому началу термодинамики правая часть(5) есть 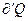
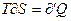
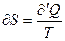
Формула(6) оказывается справедливой для любых тел, необходимо только чтобы сообщение количества тепла 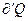
Остановимся на физической сущности энтропии.
Введем определения: состояние, осуществляемое относительно малым числом способов будет называться упорядоченным или неслучайным. Состояние, осуществляемое большим количеством способов – беспорядочным или случайным.
Тогда можно утверждать, что энтропия является количественной мерой степени беспорядка в системе. Сообщение системе количества тепла приводит к усилению теплового движения молекул, а значит и к росту энтропии. При этом, чем выше температура системы, тем меньше доля беспорядка вносимого сообщением данного 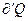
Если количество тепла сообщается системе в ходе необратимого процесса, то ее энтропия возрастает не только за счет получения тепла, но и за счет протекания необходимых процессов, поскольку необратимый процесс сопровождается ростом вероятности состояния системы, ее статистического веса
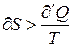
В этом случае под 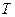
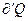
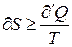
При абсолютном нуле всякая система находится в основном состоянии, т. е. состоянии с наименьшей энергией. Статический вес этого вполне определенного состояния равен единице, а значит энтропия системы равна нулю. Это соответствует теореме Нернста, согласно которой энтропия всякого тела стремится к нулю при стремлении к нулю его температуры:
Теорему Нернста называют также третьим началом термодинамики.
Связь термодинамики и статистической физики. Термодинамическая вероятность (статистический вес) состояния системы и энтропия
Ранее уже упоминалось, что с точки зрения механики описание состояния термодинамической системы через указание значений термодинамических параметров является неполным, так как для полного описания следует указать значения координат и импульсов всех частиц, составляющих термодинамическую систему. Понятно, что для всех частиц системы (при их числе порядка числа Авогадро) это требование невыполнимо. Однако можно найти какая часть (какая доля) всех частиц имеет координаты и импульсы, лежащие в интересующих нас пределах. Этим занимается статистическая механика, задачей которой является нахождение функции распределения частиц по координатам и импульсам, часто именуемой плотностью вероятности (хотя в математике функцией распределения называется функция, производная от которой и есть плотность вероятности). Эта функция показывает вероятность того, что частица имеет координаты и импульсы вблизи определенных значений. Хотя координаты и импульсы отдельных частиц системы все время изменяются в результате взаимодействий (столкновений), но в условиях термодинамического равновесия функция распределения частиц по координатам и импульсам с течением времени не изменяется. Это распределение при равновесном состоянии системы остается неизменным потому, что, несмотря на постоянное изменение каждой частицей ее положения в фазовом (координатно-импульсном) пространстве, все время происходит замещение одних частиц в фазовом пространстве другими, то есть тепловое равновесие в термодинамической системе носит динамический характер. Если состояние системы первоначально не было равновесным, то функция распределения частиц по координатам и импульсам со временем эволюционирует (процесс релаксации) к равновесному распределению, которое со временем уже очень редко испытывает заметные на макроскопическом уровне самопроизвольные отклонения (флуктуации) от распределения, соответствующего полностью равновесному.
Может возникнуть вопрос, откуда берется необратимость, если все микропроцессы обратимы (согласно принципу микроскопической обратимости)? Ответ следующий. Необратимость релаксационных процессов порождается статистическим характером макроскопически наблюдаемых явлений и вероятностным характером соответствующих им закономерностей. Одно и то же с макроскопической точки зрения состояние (та же самая функция распределения) может быть осуществлено большим числом различных микросостояний. Так, если две частицы обменялись местами в фазовом пространстве (обменялись энергиями), то это уже другое микросостояние, но с макроскопической точки зрения ничего не изменилось – сохранилось распределение частиц по фазовому пространству.
Число микроскопически различных способов W, осуществляющих одно и то же макросостояние, получило в статистической механике название термодинамической вероятности или статистического веса этого макросостояния. Для нахождения этого числа используется раздел математики, именуемый комбинаторикой. Так, например, число микроскопических способов такого распределения N молекул газа по объему, чтобы в одной половине объема оказались n молекул, а в другой остальные (N – n), находится согласно правилам комбинаторики по формуле для числа сочетаний из N по n, то есть
Эта функция, очевидно, имеет максимум при n = N/2, поскольку в этом случае также и (N – n) = N/2, а когда система отклоняется от этого равнораспределения, то, хотя в знаменателе (при постоянном числителе) один из сомножителей уменьшается, зато другой сомножитель увеличивается, и при этом в большей степени. Так, например, при отклонении на единицу числа молекул n от равнораспределения в знаменателе пропадает множитель N/2, но зато появляется (N/2 + 1), и в целом термодинамическая вероятность W(N,n) (статистический вес) уменьшается, и тем сильнее, чем больше отклонение от равнораспределения.
Все микросостояния системы при сохранении энергии системы равновероятны, то есть система пребывает в каждом из них одинаковое (хотя и очень маленькое с нашей, макроскопической точки зрения) время. Это предполагается в статистической механике. Поэтому вероятность приблизительно равномерного заполнения объема молекулами (при большом числе молекул) подавляюще велика по сравнению с тем, чтобы малая доля молекул оказалась в одной половине объема, а все остальные – в другой. Если искусственно создать неравномерность распределения молекул газа по занимаемому им объему, то такая система, будучи предоставлена себе самой, через некоторое время самопроизвольно придет к равнораспределению молекул по объему (выравнивание концентраций). Точно так же и температура, если она была сначала различной в разных частях системы, со временем выравнивается по всему объему.
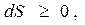 |
Теперь вспомним, что в изолированной термодинамической системе энтропия самопроизвольно возрастает и остается постоянной при достижении максимума, то есть (см. (5.5))
где знак равенства относится к обратимым процессам.
В способности энтропии самопроизвольно возрастать есть нечто чуждое нашей интуиции, воспитанной на механических представлениях. Действительно, почти все законы механики (кроме связанных с трением, но это уже не вполне механика), а также оптики и отчасти электромагнетизма, обратимы во времени (почему так легко и воспринимается нами принцип микроскопической обратимости).
Для объяснения необратимости макроскопических явлений австрийский физик Людвиг Больцман в 1872 году ввел в теорию теплоты статистические представления (которые уже отчасти использовались ранее Максвеллом при рассмотрении распределения молекул газа по скоростям). Больцман предложил каждому макроскопическому состоянию приписывать статистический вес (позднее названный Планком термодинамической вероятностью), равный числу различных механических состояний микрочастиц (образующих термодинамическую систему), отвечающих одному и тому же набору значений термодинамических параметров, определяющих в термодинамике, как известно, макроскопическое состояние термодинамической системы. При таком подходе возрастание энтропии в предоставленной себе самой термодинамической системе просто означает переход в такие состояния, термодинамические вероятности которых больше. И так должно продолжаться до тех пор, пока не будет достигнуто наиболее вероятное состояние, соответствующее максимальной энтропии. Вблизи этого состояния система и будет находиться неопределенно долгое время, испытывая иногда самопроизвольные случайные отклонения от равновесия (флуктуации), теория которых рассматривается в статистической механике, а в феноменологической термодинамике флуктуациями просто пренебрегают.
Таким образом, возрастание энтропии не является абсолютным законом в термодинамике (хотя в статистической механике это обосновывается неустойчивостью решений уравнений движения микрочастиц).
Больцман предположил следующую связь между энтропией и термодинамической вероятностью
где k – постоянная, получившая позднее название постоянной Больцмана.
Формула (10.1) явно соответствует всем требованиям, предъявляемым к энтропии. Энтропия функция аддитивная (как и все функции состояния), то есть энтропия системы равна сумме энтропий подсистем, S = SA + SB, а вероятность состояния системы (согласно теории вероятностей) равна произведению вероятностей, относящихся к подсистемам А и В, что означает W = WA·WB. Этому требованию удовлетворяет логарифмический характер функции (10.1). Отвечает она также требованию монотонного возрастания с ростом термодинамической вероятности.
Коэффициент k, входящий в формулу Больцмана, как величину универсальную, можно вычислить, если применить эту формулу к конкретной термодинамической системе.
Воспользуемся для этого, как обычно, моделью идеального газа.
Отношение вероятностей нахождения одной молекулы газа в объемах V1 и V2 (в силу хаотичности движения молекулы и, следовательно, равной вероятности нахождения в одинаковых объемах) равно отношению этих объемов, то есть
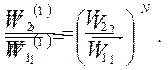 |
В силу теоремы о произведении вероятностей независимых событий, отношение вероятностей нахождения в объемах V2 и V1 всех N молекул газа равно
Поскольку согласно формуле Больцмана (10.1) изменение энтропии определяется отношением термодинамических вероятностей, то для одного моля идеального газа имеем
Теперь вычислим изменение энтропии одного моля идеального газа в обратимом изотермическом процессе по формуле Клаузиуса (5.1), используя уравнение состояния идеального газа (3.1) PV = RT и неизменность внутренней энергии при сохранении температуры, то есть δQ = PdV,
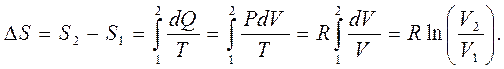 |
Из сравнения полученных двумя способами изменений энтропии обнаруживаем, что