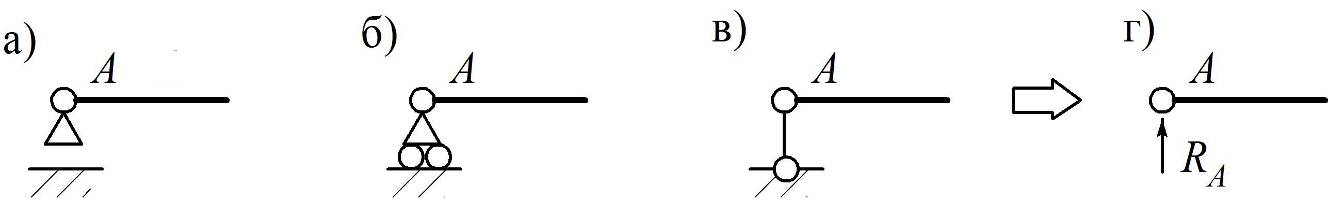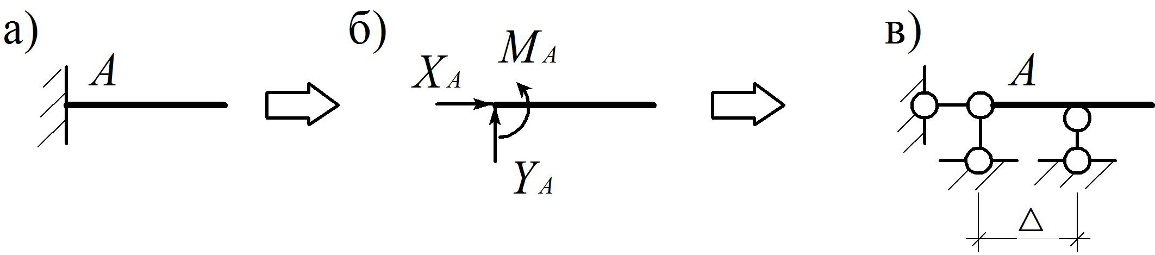что такое статика в строительстве
Раздел III. Статика сооружений
ГЛАВА 1. ВВЕДЕНИЕ
Предмет строительной механики и ее задачи
Термин «строительная механика» применяют в широком и узком смысле этого слова.
В широком смысле слова строительная механика – это раздел механики, в котором ее выводы и методы применяют для решения задач проектирования, строительства и эксплуатации сооружений. В этом значении она объединяет такие науки и дисциплины, как:
– статика и динамика сооружений;
– металлические и железобетонные конструкции
и многое другое. При этом термин «строительная механика» близок к понятиям «прикладная» или «техническая механика».
В узком смысле слова строительная механика – это, прежде всего, статика сооружений, в дальнейшем именно так мы и будем понимать этот термин.
Напомним, что если предметом теоретической механики является абсолютно твердое тело (или система таких тел), а предметом сопромата – деформируемое тело, то предметом строительной механики является система деформируемых тел.
Основная задача строительной механики – проектирование сооружений, находящихся в определенных условиях, с учетом требований прочности, жесткости, устойчивости, надежности, экономичности, эстетики и других ограничений. Для решения этой задачи нужно построить модель сооружения, выделив основные несущие элементы и определив действующую на них нагрузку. Такая модель в виде совокупности деформируемых тел, соединенных друг с другом и с землей определенными связями, и называется расчетной схемой или системой.
В зависимости от геометрических особенностей элементов системы их делят на три класса: стержневые, тонкостенные и массивы. В общем случае расчетная схема может включать в себя каждый из этих элементов. Мы ограничимся в дальнейшем рассмотрением плоских стержневых систем.
Примечания
1. Помимо основной задачи – проектирования в строительной механике, как и в сопромате, может возникнуть необходимость расчета сооружения, уже находящегося в эксплуатации. Например – при его реконструкции.
2. Решение основной задачи строительной механики сводится, прежде всего, к определению внутренних усилий. Последующий подбор сечений элементов конструкции выполняется методами сопромата либо, в зависимости от вида материала – по теории железобетонных, металлических конструкций и т.д.
Кинематический анализ сооружений
Прежде чем приступить к расчету модели сооружения, необходимо проверить: способна ли она воспринимать приложенную нагрузку, оставаясь в равновесии? При этом расчетная схема рассматривается как совокупность не деформируемых, а абсолютно жестких тел – дисков, и в отдельный класс выделяются системы, элементы которых обладают подвижностью, то есть могут смещаться относительно друг друга или относительно земли. Такое исследование структуры модели называется ее кинематическим анализом.
Поскольку подвижность системы зависит, очевидно, от вида связей, соединяющих ее элементы, вернемся к рассмотрению и уточнению этих понятий – уже встречавшихся в теоретической механике.
Связи и их реакции
Напомним, что под связью понимают тело, ограничивающее свободу перемещения выбранного рассматриваемого тела, а реакцией связи называют силу, с которой связь действует на это тело.
Будем называть связь линейной, если соответствующая ей реакция – сила и моментной, если соответствующая ей реакция – момент.
Для плоских стержневых систем можно ограничиться рассмотрением следующих видов связей.
Подвижная опора (рис. 1.1) помимо обозначения по ГОСТ (рис. 1.1, а) может на схемах изображаться так, как показано на рис. 1.1, б и 1.1, в. Она соответствует одной линейной связи, а ее реакция перпендикулярна заштрихованной опорной площадке (рис. 1.1, г).
Неподвижная опора (рис. 1.2) также допускает на схемах изображения, отличные от стандартного – на рис. 1.2, а. Очевидно, что она эквивалентна двум линейным связям (рис. 1.2, б–г).
Жесткое защемление (рис. 1.3, а) исключает не только перемещения закрепленной таким образом точки конструкции, например – балки, но и ее поворот вокруг этой точки. Оно эквивалентно двум линейным связям и одной моментной (рис. 1.3, б), либо трем линейным связям при D ® 0 (рис. 1.3, в).
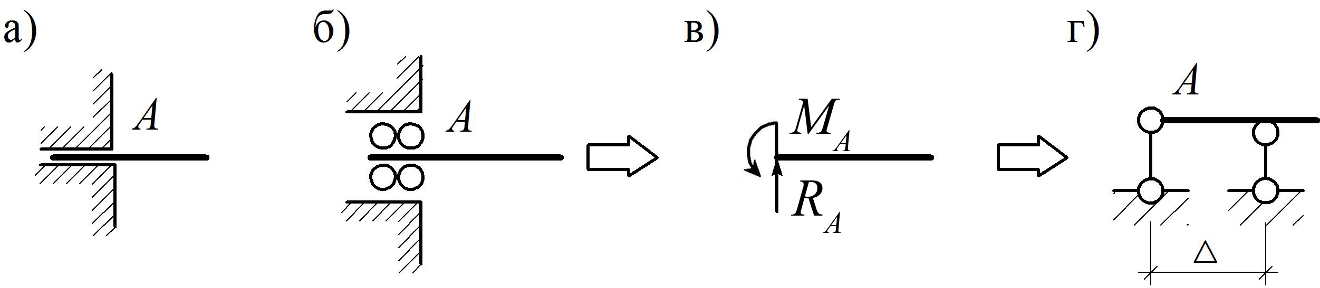
Скользящее защемление (рис. 1.4, а–б) в отличие от жесткого не препятствует смещению закрепленной таким образом точки в одном из направлений и эквивалентно линейной и моментной связям (рис. 1.4, в) либо двум линейным при D ® 0 (рис. 1.4, г).
Кратный шарнир, соединяющий N дисков, (рис. 1.5, а) будет эквивалентен (N – 1) простому шарниру (рис. 1.5, б).
Примечания
1. Результаты расчета можно улучшить, если учесть податливость соединений элементов системы.
2. Построение расчетной схемы действующего сооружения может оказаться непростой задачей, соизмеримой по сложности с самим расчетом.
Статика сооружений
Смотреть что такое «Статика сооружений» в других словарях:
СТАТИКА СООРУЖЕНИЙ — раздел строительной механики, изучающий методы расчёта сооружений на прочность, жёсткость и устойчивость при статическом действии нагрузки (Болгарский язык; Български) статика на съоръженията (Чешский язык; Čeština) statika stavebních konstrukcí… … Строительный словарь
СТАТИКА СООРУЖЕНИЙ — устар. назв. строительной механики; совр. строит. механика, кроме проблем статики, включает также и вопросы динамики сооружений … Большой энциклопедический политехнический словарь
Динамика сооружений — теория колебаний сооружений, наука о колебаниях и методах расчёта сооружений, подвергающихся действию динамических нагрузок, и способах уменьшения колебаний; раздел строительной механики (См. Строительная механика). Динамические нагрузки… … Большая советская энциклопедия
Строительная механика — наука о принципах и методах расчёта сооружений на прочность, жёсткость, устойчивость и колебания. Основные объекты изучения С. м. плоские и пространственные стержневые системы (См. Стержневая система) и системы, состоящие из пластинок (См … Большая советская энциклопедия
Некрасов, Николай Виссарионович — В Википедии есть статьи о других людях с такой фамилией, см. Некрасов. Николай Виссарионович Некрасов (Голгофский) … Википедия
Некрасов Н. В. — Н. В. Некрасов Николай Виссарионович Некрасов (1 января 1879, Санкт Петербург, Российская империя 7 мая 1940, Москва, РСФСР) российский политический деятель, инженер. Член Государственной думы III и IV созывов. Министр путей сообщения и министр… … Википедия
Некрасов Николай Виссарионович — Н. В. Некрасов Николай Виссарионович Некрасов (1 января 1879, Санкт Петербург, Российская империя 7 мая 1940, Москва, РСФСР) российский политический деятель, инженер. Член Государственной думы III и IV созывов. Министр путей сообщения и министр… … Википедия
Николай Виссарионович Некрасов — Н. В. Некрасов Николай Виссарионович Некрасов (1 января 1879, Санкт Петербург, Российская империя 7 мая 1940, Москва, РСФСР) российский политический деятель, инженер. Член Государственной думы III и IV созывов. Министр путей сообщения и министр… … Википедия
Каракис, Иосиф Юльевич — Иосиф Юльевич Каракис … Википедия
Жемочкин, Борис Николаевич — [р. 22 авг. (3 сент.) 1887] сов. ученый в области строительной механики и инженерных конструкций, действит. чл. Академии строительства и архитектуры СССР (с 1956). Генерал майор инженерно технич. службы. Окончил в 1911 Моск. инженерное училище… … Большая биографическая энциклопедия
Статика сооружений (стр. 1 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 |
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
«Нижегородский государственный архитектурно-строительный университет»
Утверждено редакционно-издательским советом
университета в качестве учебного пособия
Сжато и доступно изложены основы строительной механики в рамках, не выходящих за пределы требований ГОС. В популярной форме авторы знакомят с основными понятиями и методами этой дисциплины, необходимыми для изучения статически определимых и статически неопределимых плоских стержневых систем. Рассматривается методика построения эпюр внутренних усилий и определения перемещений. Изложен метод сил и метод перемещений, даны сведения о методе конечных элементов. Изложение сопровождается примерами, необходимыми для успешного овладения теорией и приобретения минимальных навыков в решении задач.
Илл. 66, библиогр. назв.7.
ПРЕДИСЛОВИЕ
Переход к многоуровневой системе образования проходит в условиях гуманитаризации процесса обучения и создания новых информационно-вычислительных систем. Это сопровождается значительным сокращением времени, отводимого на изучение механики у студентов традиционных специальностей, и появлением новых специальностей с одним или двухсеместровым курсом по этой дисциплине.
— статика твердого тела,
— статика деформируемого тела,
Отметим, что студенты строительных специальностей изучают эти разделы механики в соответствующих курсах: теоретической механики, сопротивления материалов и строительной механики. Поэтому нетрудно понять, что успешное овладение основами механики в рамках сокращенной программы представляет непростую задачу, как для лектора, так и для студентов. И первым шагом на пути её решения является определение целей этого курса. Для студентов-архитекторов они сформулированы так:
— научить анализировать существующие конструктивные решения, понимать работу сооружения в целом и оценивать ту роль, которую играют отдельные элементы ансамбля, устанавливать функциональную связь между воздействиями, внутренними усилиями и формой сооружения;
— способствовать осознанному, свободному и целенаправленному решению основной задачи архитектурного проектирования – поиску новых форм и совершенных решений;
— ознакомить с основными понятиями и методами строительной механики и помочь формированию рационального и логического мышления.
Достижение намеченных целей требует тщательной подготовки учебной программы и её методического обеспечения.
Настоящее пособие является попыткой содействовать решению этой задачи для третьего раздела курса – статики сооружений. Его содержание не претендует на полноту и отражает точку зрения авторов на то, каким должен быть начальный курс этой дисциплины для архитекторов.
В частности, было принято решение ограничиться изучением плоских стержневых систем, которые в пособии представлены балками, рамами, фермами и арками. Изложена методика построения эпюр и определения перемещений, рассмотрены метод сил и метод перемещений. Даны понятия о расчете статически неопределимых систем методом конечных элементов.
Замечания в конце ряда параграфов предназначены для критически настроенных читателей и могут быть оставлены без внимания при первом чтении.
Авторы благодарят студентку факультета архитектуры и градостроительства С. Смирнову за выполненные для этого пособия рисунки.
1.1. Предмет строительной механики и ее задачи
Термин «строительная механика» применяют в широком и узком смысле этого слова.
В широком смысле – строительная механика это раздел механики, в котором ее выводы и методы применяют для решения задач проектирования, строительства и эксплуатации сооружений. В этом значении она объединяет такие науки и дисциплины как:
– статика и динамика сооружений;
– металлические и железобетонные конструкции
и многое другое. При этом термин «строительная механика» близок к понятиям «прикладная» или «техническая механика».
В узком смысле слова строительная механика – это, прежде всего, статика сооружений, в дальнейшем именно так мы и будем понимать этот термин.
Напомним, что если предметом теоретической механики является абсолютно твердое тело (или система таких тел), а предметом сопромата – деформируемое тело, то предметом строительной механики является система деформируемых тел.
Основная задача строительной механики – проектирование сооружений, находящихся в определенных условиях с учетом требований прочности, жесткости, устойчивости, надежности, экономичности, эстетики и других ограничений. Для решения этой задачи нужно построить модель сооружения, выделив основные несущие элементы и определив действующую на них нагрузку. Такая модель в виде совокупности деформируемых тел, соединенных друг с другом и с землей определенными связями, и называется расчетной схемой или системой.
В зависимости от геометрических особенностей элементов системы их делят на три класса: стержневые, тонкостенные и массивы. В общем случае расчетная схема может включать в себя каждый из этих элементов. Мы ограничимся в дальнейшем рассмотрением плоских стержневых систем.
1. Помимо основной задачи – проектирования в строительной механике, как и в сопромате, может возникнуть необходимость расчета сооружения, уже находящегося в эксплуатации. Например – при его реконструкции.
2. Решение основной задачи строительной механики сводится, прежде всего, к определению внутренних усилий. Последующий подбор сечений элементов конструкции выполняется методами сопромата либо, в зависимости от вида материала, – по теории железобетонных, металлических конструкций и т. д.
1.2. Кинематический анализ сооружений
Прежде чем приступить к расчету модели сооружения, необходимо проверить: способна ли она воспринимать приложенную нагрузку, оставаясь в равновесии? При этом расчетная схема рассматривается как совокупность не деформируемых, а абсолютно жестких тел – дисков, и в отдельный класс выделяются системы, элементы которых обладают подвижностью, то есть могут смещаться относительно друг друга или относительно земли. Такое исследование структуры модели называется ее кинематическим анализом.
Поскольку подвижность системы зависит, очевидно, от вида связей, соединяющих ее элементы, вернемся к рассмотрению и уточнению этих понятий – уже встречавшихся в теоретической механике.
1.2.1. Связи и их реакции
Напомним, что под связью понимают тело, ограничивающее свободу перемещения выбранного рассматриваемого тела, а реакцией связи называют силу, с которой связь действует на это тело.
Будем называть связь линейной, если соответствующая ей реакция – сила и моментной, если соответствующая ей реакция – момент.
Для плоских стержневых систем можно ограничиться рассмотрением следующих видов связей.
Подвижная опора (рис. 1.1) помимо обозначения по ГОСТу (рис. 1.1, а) может на схемах изображаться так, как показано на рис. 1.1, б и 1.1, в. Она соответствует одной линейной связи, а ее реакция перпендикулярна заштрихованной опорной площадке (рис. 1.1, г).
Неподвижная опора (рис. 1.2) также допускает на схемах изображения, отличные от стандартного – на рис. 1.2, а. Очевидно, что она эквивалентна двум линейным связям (рис. 1.2, в – г).
Жесткое защемление (рис. 1.3, а) исключает не только перемещения закрепленной точки балки, но и ее поворот вокруг этой точки. Оно эквивалентно двум линейным связям и одной моментной (рис. 1.3, б), либо трем линейным связям при D ® 0 (рис. 1.3, в).
Скользящее защемление (рис. 1.4, а – б) в отличие от жесткого не препятствует смещению закрепленной таким образом точки в одном из направлений и эквивалентно линейной и моментной связям (рис. 1.4, в) либо двум линейным при D ® 0 (рис. 1.4, г).
Кратный шарнир, соединяющий N дисков, (рис. 1.5, а) эквивалентен (N – 1) простому шарниру (рис. 1.5, б).
1. Результаты расчета можно улучшить, если учесть податливость соединений элементов системы.
2. Построение расчетной схемы действующего сооружения может оказаться непростой задачей, соизмеримой по сложности с самим расчетом.
1.2.2. Степени свободы и статическая определимость системы
Все системы в механике можно разделить на два класса: неизменяемые системы (НС) и изменяемые системы (ИС).
Определение 1.1. Неизменяемыми или неподвижными будем называть системы, элементы которых не могут перемещаться относительно друг друга или относительно земли, если они являются абсолютно твердыми, то есть недеформируемыми.
Изменяемыми или подвижными будем называть системы, элементы которых могут перемещаться относительно друг друга или относительно земли, оставаясь абсолютно твердыми
НС могут воспринимать любую нагрузку, ИС – только определенные виды нагрузок.
Например, рама на рис. 1.10, а является НС и может воспринимать как горизонтальную, так и вертикальную нагрузку, оставаясь в положении равновесия. А раму на рис. 1.10, б можно загрузить вертикальной нагрузкой, но она не способна воспринимать горизонтальную нагрузку, под действием которой она придет в движение – подобно незакрепленному на рельсах монтажному крану под действием ветра.
Все неизменяемые системы делятся на статически определимые (СОС) и статически неопределимые системы (СНС).
Напомним, что СОС – это системы, для которых число неизвестных реакций внешних и внутренних связей не превышает максимально допустимого числа уравнений статики, которые можно составить для их определения.
Если число неизвестных больше максимально допустимого числа уравнений, система называется СНС. При этом разность между числом неизвестных и числом уравнений называется степенью статической неопределимости системы.
Чтобы описать изменяемые системы введем следующее
Определение 1.2. Под степенью свободы системы – W будем понимать минимальное число параметров, определяющих ее положение в пространстве.
Если два свободных диска на плоскости (W = 6) соединить одной линейной связью C1C2, получим систему с пятью степенями свободы (рис. 1.7), поскольку к трем параметрам для первого диска добавятся углы j1 и j2, определяющие положение стержня C1C2 относительно диска Д1 и диска Д2 относительно точки C2. Аналогично, система двух дисков, соединенных двумя линейными связями (или шарниром) будет иметь 4 степени свободы.
Естественно предположить, что всякое наложение дополнительной связи уменьшает степень свободы системы на единицу, поэтому для произвольной плоской системы ее можно найти по формуле:
где W* – предполагаемая или условная степень свободы системы;
Ш – число простых шарниров, соединяющих диски друг с другом;
СО – число опорных связей.
Как видим, при рассмотрении любой системы возможны три варианта:
1) W* > 0 – система заведомо подвижна;
2) W* = 0 – система имеет минимальное число связей, необходимых для ее неизменяемости;
3) W* 0, W* = 0) подразделяются на:
– геометрически изменяемые системы (ГИС);
– мгновенно изменяемые системы (МИС).
Мгновенно изменяемые отличаются от ГИС тем, что допускают не конечные – как рама на рис. 1.10, б, – а только бесконечно малые перемещения. При этом значения параметров, о которых идет речь в определении 1.4, у ГИС остаются постоянными, а у МИС – изменяются при перемещении.
Кроме того, переход неподвижных статически определимых систем в МИС может сопровождаться появлением бесконечно больших опорных реакций.
Рассмотрим, например, НС на рис. 1.11, а. Для определения опорной реакции RB составим уравнение равновесия: SМА = 0, откуда найдем: RB = Pa/D. Эта рама переходит в МИС на рис. 1.11, б при критическом значении параметра D = 0. Нетрудно видеть, что предел RB при D ® 0 равен бесконечности.
Это может привести к разрушению реальной конструкции, поэтому такие МИС не применяют в строительстве.
Термин «мгновенно изменяемая система», подчеркивает, что под действием приложенной нагрузки реальная деформируемая система может занять новую конфигурацию, для которой значение параметра станет отличным от критического. При этом в рассматриваемом примере (рис. 1.11, б) точка В сместится вниз и реакция RB примет конечное значение.
Итак, мы выяснили, что принадлежность системы к классу МИС крайне нежелательна. Поэтому перечислим некоторые признаки МИС:
1) Два диска, соединенные шарниром, связаны с остальной частью системы или с землей при помощи двух других шарниров, лежащих на одной прямой с первым (рис. 1.12).
2) Диск, прикреплен к системе или к земле при помощи трех линейных связей, у которых линии действия реакций параллельны (рис. 1.13) или пересекаются в одной точке (рис. 1.14).
1. МИС на рис. 1.11, б соответствует первому из приведенных признаков, роль второго диска выполняет подвижная опора В. Диск Д1 на рис. 1.14 выполняет роль третьей линейной связи по отношению к диску Д2.
2. Приведенные признаки МИС не являются исчерпывающими, то есть если исследуемая модель не отвечает им, то это не означает, что она не будет принадлежать к этому классу. Самым общим является аналитический метод исследования систем, основанный на рассмотрении уравнений равновесия для определения их опорных реакций.
3. Поскольку кинематический анализ связан с рассмотрением системы абсолютно твердых тел, он мог бы изучаться в курсе теоретической, а не как традиционно – строительной механики. Кстати, в [5] на стр. 26-28 можно найти несколько МИС, ошибочно включенных в задание, где требуется определить опорные реакции составной конструкции.
1.2.4. Способы образования и структурный анализ
Рассмотрим два способа образования стержневых систем, которые будут неизменяемыми и статически определимыми. Другими словами, выясним, при каких условиях соотношение:
будет не только необходимым, но и достаточным для образования таких систем.
1. Соединение диска с землей (соединение двух дисков). Диск прикреплен к земле при помощи шарнира и линейной связи, линия действия реакции которой не проходит через этот шарнир (рис. 1.15, а).
Шарнир А можно заменить двумя линейными связями, линии действия которых пересекаются в точке, через которую не должна проходить линия действия реакции третьей линейной связи (рис. 1.15, б).
Если диск Д2 присоединяется не к земле, а к диску Д1, получим систему, которую можно принять за новый диск, имеющий ту же степень свободы, что и диск Д1.
Этот способ образования систем называется диадным – от названия простейшей фермы, образованной из двух стержней, соединенных шарниром В. Роль первого стержня выполняет незагруженный диск АВ (рис. 1.15, а).
2. Соединение двух дисков с землей (соединение трех дисков). Два диска соединены друг с другом и с землей при помощи трех шарниров, не лежащих на одной прямой (рис. 1.16, а).
Аналогично соединяются три диска, при этом каждый шарнир можно заменить двумя линейными связями, у которых точки пересечения линий действия реакций также не должны лежать на одной прямой (рис. 1.16, б).
Этот способ образования систем называется способом трехшарнирной арки. Очевидно, что он является более общим и сводится к диадному, если диски Д1 и Д2 незагружены и, значит, их можно заменить стержнями АС и ВС, соединенными в точке С (рис. 1.16, а).
Нетрудно заметить, что ограничения, налагаемые на способы образования системы, нужны для того, чтобы избежать появления МИС.
Структурный анализ. Заключается в исследовании уже существующей системы с точки зрения возможности ее образования двумя рассмотренными способами.
– системы, образованные из нескольких дисков, образуют один новый диск;
– при условии (1.5) ни один из присоединенных дисков не должен иметь лишних связей;
– вновь образованная система будет неподвижной (НС) и статически определимой (СОС).
Пример 1.3. Выполнить структурный анализ рамы (рис. 1.17).
Решение. Система состоит из пяти дисков, соединенных простыми шарнирами E, G, F и кратным шарниром D, эквивалентным двум простым.
Условная степень свободы по формуле (1.5):
Диски Д1 и Д2 образуют по способу трехшарнирной арки новый диск Д1-2, жестко связанный с землей. К диску Д1-2 диадным способом при помощи шарнира D и линейной связи C присоединяется диск Д3, который образует новый и неподвижный относительно земли диск Д1-3. Наконец, к диску Д1-3 присоединяется диада Д4, Д5, образуя диск Д1-5. Таким образом, заданная система является СОС и НС. ·
Следует отметить, что системы могут быть образованы и другими способами – отличными от диадного и способа трехшарнирной арки, поэтому основанный на них структурный анализ не является универсальным методом исследования системы. Например, с его помощью нельзя дать ответ на вопрос об изменяемости рамы на рис. 1.18, поскольку ее нельзя образовать двумя указанными способами.
1.2.5. Аналитическое исследование системы
Как уже отмечалось, этот метод исследования систем является самым общим.
Суть метода. Уравнения равновесия для определения опорных реакций исследуемой системы можно представить в виде:
где [A] – матрица коэффициентов при неизвестных;
<X> – вектор-столбец неизвестных опорных реакций;
<B> – вектор-столбец нагрузки.
При этом для СОС любому вектору <B> однозначно соответствует единственный вектор <X>, что возможно только при условии: det [A] ¹ 0.
Учитывая, что в силу (1.5) СОС одновременно являются НС, можно сделать вывод, что необходимым и достаточным условием неподвижной системы будет:
Наоборот, необходимым и достаточным условием подвижной системы является:
Таким образом, для кинематического анализа системы достаточно вычислить определитель матрицы соответствующей системы алгебраических уравнений. Но можно избежать даже этой процедуры, учитывая некоторые сложности которые она вызывает уже при четвертом порядке определителя.
Метод нулевой нагрузки. Рассмотрим однородную систему уравнений, соответствующую (1.6):
Известно, что она имеет только нулевое решение, если det [A] ¹ 0, и наоборот – условием ненулевого решения будет: det [A] = 0.
Отсюда – следующее правило:
1) Если система (1.9) имеет решение <X> = <0>, то соответствующая механическая система является неподвижной;
2) Если система (1.9) имеет решение <X> ¹ <0>, то соответствующая механическая система является подвижной.
Пример 1.4. Выполнить кинематический анализ рамы (рис. 1.18).
Решение. Воспользуемся методом нулевой нагрузки, применив графический способ решения (рис. 1.19).
Из условия равновесия диска АЕ следует, что реакции RA и RE направлены по прямой АЕ (аксиома 2).
Из условия равновесия диска FCG аналогично находим линию действия реакции RG, проходящей вдоль прямой GL.
1. Подобно тому, как СНС, которые мы рассмотрим в 4 главе, могут быть статически неопределимыми внешним и внутренним образом, можно говорить о системах, изменяемых аналогично. Поэтому в общем случае вектор <X> в системе (1.6) должен содержать компоненты реакций не только внешних, но и внутренних связей.
2. Отметим, что в последнем примере 1.4 мы остаемся в рамках аналитического метода анализа геометрической изменяемости системы, несмотря на то, что при реализации метода нулевой нагрузки применялся графический способ определения реакций связей. Такой прием вполне оправдан, поскольку формальный подход потребовал бы вычисления определителя десятого порядка.
3. Анализ системы уравнений (1.6), независимо от условия (1.5), позволяет получить полную характеристику механической системы, включая степени ее свободы и статической неопределимости.
4. При построении модели сооружения ее параметры определяются с некоторой степенью точности, поэтому опасность на практике представляют не только МИС, но и близкие к ним – у которых det [A] » 0.
1.3. Основные уравнения строительной механики
Математическая сторона основной задачи строительной механики основана на зависимостях, полученных в сопромате. Напомним их на примере напряженно-деформированного состояния элемента рамы, для которого – в отличие от балки – поперечный изгиб сопровождается дополнительным растяжением или сжатием.
Пусть такой элемент длиной dx расположен в локальной системе координат Oxy, где ось Ox направлена по оси стержня, и загружен распределенной нагрузкой интенсивностью qx и qy вдоль Ox и Oy соответственно (рис. 1.20).
Напряженно-деформированное состояние стержня определяется девятью компонентами:
– деформациями (κ, g, e).
Уравнения для определения этих функций можно разделить на три группы:
Статические уравнения – связывают внутренние усилия (рис. 1.20, б) с заданной нагрузкой:
Геометрические уравнения – выражают деформации через перемещения, показанные на рис. 1.20, б, в:
Физические уравнения – представляют собой зависимости между внутренними усилиями и деформациями:
где E – модуль Юнга;
F – площадь поперечного сечения стержня;
J – момент его инерции;
m – коэффициент, учитывающий неравномерность распределения касательных напряжений в поперечном сечении стержня.
Отметим, что выражения EJ и EF в (1.12) называются жесткостями стержня при изгибе и растяжении (сжатии) соответственно.
При решении системы уравнений (1.10) – (1.12) возможны два варианта:
1) внутренние усилия M, Q, N, удается найти из системы уравнений (1.10), не обращаясь к остальным уравнениям – это СОС;
2) внутренние усилия можно найти только путем совместного решения всех девяти уравнений – это СНС.
В последнем случае при решении этих уравнений возможны два подхода:
– в качестве основных неизвестных выбирают усилия M, Q, N, выражая все остальные через них – это решение в форме метода сил;
– в качестве основных неизвестных выбирают перемещения u, v, q – это решение в форме метода перемещений.
Системы, описываемые линейными уравнениями (1., называются линейно деформируемыми. Для них справедлив принцип суперпозиции, в соответствии с которым:
Внутренние усилия, перемещения и деформации от заданной нагрузки (или иного воздействия) можно найти как сумму соответствующих величин от каждой нагрузки в отдельности.
1. Первое из статических уравнений (1.10) получается из условия равновесия рассматриваемого элемента рамы. Полагая в его пределах qx = const, и составляя уравнение SX = 0, получим:
откуда и следует искомая зависимость. Два других уравнения из (1.10) – это дифференциальные зависимости Журавского.
2. Первое из физических уравнений (1.12) представляет собой дифференциальное уравнение изогнутой оси балки:
Второе уравнение в предпосылке равномерного распределения касательных напряжений в поперечном сечении стержня (m =1) выражает закон Гука при сдвиге:
При этом мы не уточняем смысл коэффициента m по причине, которая будет указана в § 3.5. Последнее из физических уравнений (1.12) – это закон Гука при ЦРС:
3. В дальнейшем, если не будет оговорено особо, мы будет по-прежнему применять обозначение Oxy для глобальной системы координат, связанной с конструкцией в целом.
ГЛАВА 2. РАСЧЕТ СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ СТЕРЖНЕВЫХ СИСТЕМ
2.1. Свойства статически определимых систем
Эти свойства определяются тем обстоятельством, что для нахождения внутренних усилий в таких системах достаточно рассмотреть только уравнения статики (1.10), не обращаясь к геометрическим (1.11) или физическим (1.12) уравнениям.
1) Внутренние усилия не зависят от геометрии поперечных сечений и материала стержней.
Действительно, физические константы E, G, n и геометрические характеристики сечений F, J не входят в уравнения равновесия (1.10).
2) Температурные и кинематические воздействия не вызывают появления реакций и внутренних усилий в СОС.
В самом деле, эти воздействия не входят в правую часть системы алгебраических уравнений для определения опорных реакций (1.6), поэтому они примут вид:
откуда следует, что <X> = <0>, так как для СОС det [A] ¹ 0.
3) Если нагрузку, приложенную к какому-либо диску составной системы заменить статически эквивалентной, то реакции и внутренние усилия в остальных дисках не изменятся.
4) Если изменить конфигурацию какого-либо диска составной системы, сохранив расположение опор и соединительных шарниров, то реакции и внутренние усилия в остальных дисках не изменятся.
5) Устранение в СОС любой связи, усилие в которой отлично от нуля, приводит к разрушению всей системы.
Напомним, что неподвижные СОС имеют минимальное число связей, необходимых для их образования, поэтому устранение любой такой связи превращает систему в механизм.