что такое статически неопределимая система

Статически неопределимая система

Полезное

Смотреть что такое «Статически неопределимая система» в других словарях:

Статически неопределимая система — в строительной механике, геометрически неизменяемая система, в которой реакции связей (усилия в опорных закреплениях, стержнях и т. п.) не могут быть определены с помощью одних уравнений статики, а требуется совместное рассмотрение… … Википедия

СТАТИЧЕСКИ НЕОПРЕДЕЛИМАЯ СИСТЕМА — (в строительной механике) геометрически неизменяемая система, в которой для определения всех реакций связей (усилий в опорных закреплениях, стержнях и т. п.) необходимы, помимо уравнений статики, дополнительные уравнения, характеризующие… … Большой Энциклопедический словарь

статически неопределимая система — (в строительной механике), геометрически неизменяемая система, в которой для определения реакций связей (усилий в опорных закреплениях, стержнях и т. п.) необходимы, помимо уравнений статики, дополнительные уравнения, характеризующие деформации… … Энциклопедический словарь

СТАТИЧЕСКИ НЕОПРЕДЕЛИМАЯ СИСТЕМА — в строительной механике геометрически неизменяемая система, в к рой для определения усилий во всех элементах и опорных связях необходимы, помимо ур ний статики, дополнит. ур ния, характеризующие деформации системы … Большой энциклопедический политехнический словарь

Статически определимая система — в строительной механике, система конструкций, в которой реакции всех связей (усилия в опорных закреплениях, стержнях и т.п.) при любой нагрузке могут быть определены с помощью уравнений статики (см. Строительная механика). С. о. с.… … Большая советская энциклопедия

Статически определимая система — Статическая система называется статически определимой, если число опорных реакций соответствует числу степеней свободы, и величины опорных реакций по принципу механического равновесия можно определить из величин внешних нагрузок. Все другие… … Википедия

система статически неопределимая — статически неопределимая система Геометрически неизменяемая, система, содержащая связи, реакции которых при произвольной статической нагрузке могут быть найдены лишь из совместного рассмотрения условий статики и условий, характеризующих… … Справочник технического переводчика

СИСТЕМА СТАТИЧЕСКИ НЕОПРЕДЕЛИМАЯ — конструктивная система, количество наложенных связей в которой превышает число уравнений статического равновесия (Болгарский язык; Български) статически неопределима система (Чешский язык; Čeština) staticky neurčitá soustava (Немецкий язык;… … Строительный словарь

Система, статически неопределимая — геометрически неизменяемая система, содержащая связи, реакции которых при заданной нагрузке могут быть найдены лишь при совместном рассмотрении условий статики и условий, характеризующих деформацию данной системы. Источник: Справочник дорожных… … Строительный словарь

Ферма (технич.) — Ферма (франц. ferme, от лат. firmus √ крепкий, прочный), несущая конструкция, состоящая из прямолинейных стержней, узловые соединения которых при расчёте условно принимаются шарнирными. Ф. применяют главным образом в строительстве (покрытия… … Большая советская энциклопедия

Источник

Статически неопределимые системы

Вы будете перенаправлены на Автор24

Сущность статически неопределимых систем

Статически неопределимая система – это геометрически неизменяемая система, в которой усилия в опорах, стержнях и т.д. не могут определяться с помощью одних лишь уравнений статики. Такие системы требуют совместное рассмотрение статических уравнений равновесия совместно с дополнительными уравнениями, которые характеризуют деформации системы.

Статически неопределимая система характеризуется наличием «лишних» связей, которые допускается удалить, не нарушив при этом геометрической неизменяемости системы. Количество дополнительных уравнений, которые следует составить для определения усилий, будет равно числу «лишних» связей (лишних неизвестных). Данное число еще называют степенью статической неопределимости системы, о ней также пойдет речь в настоящей статье. Для определения усилий в подобных системах чаще всего используют метод сил и метод перемещений. Метод сил также используется при механизированном расчете строительных конструкций.

Из вышеизложенного следует, что степень статической неопределимости системы может быть найдена по формуле:

В качестве примера можно рассмотреть случай с заделанной с одной стороны консольной балкой. Поскольку в такой опоре существует три опорные реакции, данная система будет являться статически определимой, ведь из курса теоретической механики известно, что для плоской системы сил можно составить только три уравнения равновесия.

Если добавить к вышеописанной системе еще одну опору, например, шарнирно-подвижную, то такая балка становится статически неопределимой один раз, поскольку количество неизвестных увеличивается до четырех, а уравнений равновесия для данного случая можно составить только три.

Готовые работы на аналогичную тему

Таким образом, если к рассматриваемой системы прибавлять последовательно по одной опоре, то степень статической неопределимости также будет увеличиваться на единицу. В таких случаях для определения величины и направления неизвестных усилий потребуется составление дополнительных уравнений.

Процесс определения усилий в «лишних» связях системы называют раскрытием статической неопределимости. Существует ряд способов раскрытия статической неопределимости, их принцип основан на двух положениях. Первое основано на равенстве нулю соответствующих точек системы на ее опорах, второе – на совместности деформаций всех или нескольких элементов системы.

Степень статической неопределимости

Следует заметить, что перед расчетом любой системы методами строительной механики необходимо определить степень статической неопределимости этой системы. Как уже упоминалось выше, для простейших систем (балок и элементарных рам) степень статической неопределимости будет равна числу «лишних» связей.

Дополнительные связи в системах можно удалить, не нарушив при этом их геометрической неизменяемости. Особенностью большинства этих связей является то, что реакции от внешних усилий в них определить нельзя с помощью одних лишь уравнений статики. Такие связи называют условно необходимыми. Наряду с ними в системах часто имеются связи, усилия в которых можно определить из условий равновесия. Такие связи называют абсолютно необходимыми. Удаление этих связей приводит к преобразованию системы в геометрически неизменяемую или мгновенно изменяемую.

Следует различать внешне и внутренне статически неопределимые системы. Первые представляют собой системы, в которых имеются только «лишние» внешние связи (например, опорные закрепления). Внутренне статически неопределимыми называют системы, обладающие «лишними» связями, которые обычно вводятся для взаимного соединения частей системы.

Однако, для определения степени статической неопределимости сложной системы следует понимать разницу между простым и сложным шарниром. Простым называют шарнир, соединяющий два стержневых элемента. Шарнир, соединяющий три и более стержня, называют сложным. Количество простых шарниров в системе можно определить по формуле:

Ш = СТ – 1,

где СТ – количество стержневых элементов в узле.

Источник

iSopromat.ru

Статически неопределимыми называют системы, в которых для определения опорных реакций либо внутренних усилий одних только уравнений статики недостаточно.

Статическая неопределимость возникает из-за наличия дополнительных или «лишних» связей.

Здесь под словом «лишние» понимаются дополнительные опоры (связи) добавление которых не влияет на геометрическую неизменяемость системы в целом.

Дополнительные опоры увеличивают прочность и жесткость систем, что позволяет делать их более экономичными.

Степень статической неопределимости систем

Степень статической неопределимости n определяется по формуле:

где,
k – количество неизвестных усилий (реакций связи),
m – количество уравнений равновесия которые можно составить для данной системы.

Системы, для которых n=1 называют однажды статически неопределимыми, n=2 – дважды СН и т.д.

Примеры статически неопределимых систем

В качестве примера рассмотрим следующий случай:

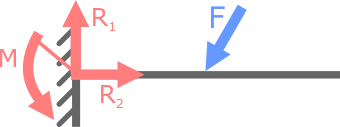
Консольная балка, закрепленная только в жесткой заделке – статически определима, так как в опоре данной схемы могут иметь место не более трех опорных реакций (вертикальная и горизонтальная силы и момент).

Как известно из курса теоретической механики для плоской системы сил можно составить только три уравнения равновесия. Трех уравнений для определения трех неизвестных вполне достаточно.

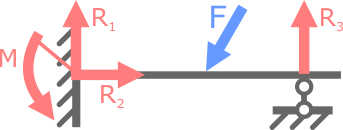
Теперь, если добавим к рассматриваемой схеме еще одну опору, например шарнирно-подвижную, то балка становится статически неопределимой, так как количество неизвестных связей увеличилось до четырех, а уравнений равновесия по-прежнему можно составить только три.

В данном случае для расчета опорных реакций не хватает еще одного уравнения, т.е. система один раз (однажды) статически неопределима.

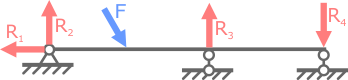
Если к данной системе последовательно добавлять опоры, то степень неопределимости также будет возрастать.

В таких случаях для расчета величины и направления неизвестных усилий потребуются дополнительные уравнения.

Другие примеры СНС

Примеры однажды статически неопределимых систем (n=1):

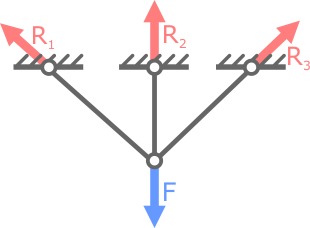
Статически неопределимая стержневая система

Раскрытие статической неопределимости

Расчет усилий в лишних связях называется раскрытием статической неопределимости системы.

Существует несколько способов раскрытия статической неопределимости, принцип которых основан на:

Наиболее универсальным из них является метод сил.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Статически неопределимые системы

Статически неопределимые системы. Метод сравнения деформаций

Основные понятия о степенях свободы и статической неопределимости

Вначале рассмотрим вопрос о возможностях перемещения механических систем — степенях свободы. Это изучалось в курсе теоретической механики. Однако, считаем необходимым повторить это и в курсе сопротивления материалов.

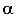
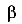
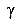
Пусть абсолютно жесткое тело находится в пространства (рис. 86 а). Выберем произвольную систему координатных осей — Х, У, Z. В этом пространстве тело имеет возможность совершить шесть независимых движений — смещения по направлению каждой оси U, V, W и повороты около этих осей , , . Таким образом, тело имеет шесть степеней свободы.

Теперь, поместим тело уже на плоскости, образованной координатными осями X и Y (рис. 86 б). Количество независимых движений этого тела равно трем — смещения по направлениям осей X и У —U и V, а также поворот около начала координат а. Количество степеней свободы равно трем.

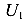
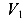
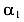
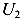
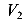
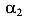
Поместим на плоскость два абсолютно жестких не связанных друг с другом тела (рис. 86 в). Количество степеней свободы этой системы равно шести — три степени свободы одного тела , , , и три степени свободы другого тела , , .

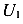
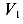
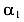
Однако, элементы конструкций чаще всего как-то связаны друг с другом и опорой. Каждая связь уменьшает количество степеней свободы на единицу. Соединим два тела шарниром (рис. 86 г). Полученная система в цепом может совершить движения по направлению оси X и оси Y — и а также поворачиваться около начала координат .

Кроме того, одно тело может поворачиваться относительно другого ct| за счет связывающего их шарнира. Таким образом, шарнир уменьшил количество степеней свободы на два. Значит, установленный шарнир ограничивает возможность движений системы (рис. 86 г) на два, то есть шарнир, соединяющий оба тела, имеет две связи.

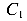
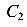
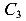
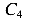
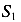
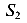
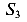
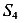
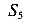
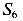
На рисунке (рис. 86 д) показана балка, разрезанная на пять частей четырьмя шарнирами , , и и опирающаяся на шарнирно неподвижную опору и шарнирно подвижные опоры, , и . Части балки в плоскости, образованной двумя осями X и Y в сумме имеют 15 степеней свободы. Шарнирно неподвижная опора слева и четыре шарнирно подвижные опоры ограничивают возможность шести

смещениям системы, а четыре шарнира, каждый из которых имеет по две связи, ограничивают возможность движений по восьми направлениям. Таким образом, система имеет только одну степень свободы 15-6-8=1.

Сделанные выше рассуждения, очень важны при исследовании статически неопределимых механических систем. Дадим определение статически неопределимым системам.

Статически неопределимыми системами называются такие системы, у которых количество неизвестных реакций или внутренних сил превышает число уравнений равновесия. В этом случае реакции и внутренние силы методами статики найдены быть не могут. Любая статически неопределимая система характеризуется степенью статической неопределимости, которая равна разности числа неизвестных и числа линейно независимых уравнений равновесия. Статическая неопределимость может быть внутренней и внешней (рис.89).

Таким образом, для определения неизвестных в статически неопределимых системах следует иметь такое количество уравнений, которое было бы равно числу неизвестных. Если количества уравнений равновесия не хватает, то необходимо дополнительно составить уравнения, но уже не по условию статического равновесия, а из каких-то других соображений, например, по условию совместности деформаций элементов рассматриваемой конструкции. Такие уравнения будем называть дополнительными. Число дополнительных уравнений должно быть равным степени статической неопределимости механической системы.

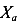
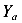
На рисунке (рис.87 а) показана балка, опирающаяся на три опоры. Левая опора является шарнирно неподвижной и имеет две связи. Поэтому в ней появляются две реакции и . Опоры В и С шарнирно подвижные,

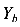
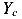
имеют по одной связи. В каждой из них появляется по одной реакции и . То есть балка имеет четыре связи. Но балку следует рассматривать как тело расположенное в плоскости. Поэтому она имеет три степени свободы — перемещения по вертикальному и горизонтальному направлениям и поворот около неподвижной точки. Значит, степень статической неопределимости балки равна n=4-3=1 и требуется составить одно дополнительное уравнение.

Дополнительное уравнение присоединяется к трем уравнениям равновесия. В результате получается система, содержащая четыре уравнения, то есть столько, сколько неизвестных. Решением этой системы уравнений, определяются все неизвестные — внешние (реакции) и внутренние (внутренние силы). Рассмотренная балка имеет внешнюю статическую неопределимость.

На рисунке (рис. 87 б) показана рама, расположенная в плоскости XY и опирающуюся на шарнирно неподвижную опору А с двумя связями и шарнирно подвижную опору В, с одной связью. Если рассматривать раму как одно тело, имеющую три степени свободы в плоскости XY, то ее следует рассматривать как статически определимую. В сумме опоры А и В имеют три связи, соединяющие раму с опорой. Поэтому количество уравнений равновесия равно количеству неизвестны сил (реакций) в этих связях. А это значит, что неизвестные реакции могут быть найдены только из уравнений равновесия. Значит рама внешне статически определимая.

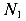
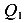
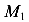
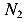
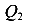
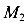
Если нам понадобиться найти не только реакции, но и внутренние силы в сечениях рамы, то уравнений статического равновесия не хватит. Вертикальным сечением разделим раму на две части — левую и правую, отбросим правую часть и рассмотрим левую (рис 87 б). Отброшенная правая часть действует на левую часть внутренними силами , , и , , . То есть всего неизвестных шесть, а уравнений равновесия можно составить только три. Очевидно, что уравнений недостаточно и требуется составить еще три дополнительных уравнения уже не по условию равновесия, а из условия совместности деформаций. Следовательно, рама внутренне трижды статически неопределимая.

Статически неопределимые системы являются более экономичными и часто применяются в строительстве. Однако, расчет таких конструкций более трудоемкий и сложный чем статически определимых конструкций.

Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:

Дополнительные страницы которые вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Пособие по статически неопределимым системам

Загрузить всю книгу

Титульный лист

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Тольяттинский государственный университет

Кафедра «Материаловедение и механика материалов»

«Расчеты статически неопределимых систем в условиях изгиба»

Авторы–составители: доцент Е.П.Гордиенко, старший преподаватель И.Т.Каратеева, старший преподаватель И.В.Котова

Под общей редакцией к.т.н., доцента Гавриловой Т.Ф.

Расчеты статически неопределимых систем в условиях изгиба: /Лабораторный практикум/ Составители: Е.П.Гордиенко, И.Т.Каратеева, И.В.Котова/под ред. к.т.н., доцента Гавриловой Т.Ф. Тольятти: ТГУ, 2005.–48 с.

Пособие предназначено для изучения студентами темы «расчеты статически неопределимых систем в условиях изгиба» в курсе сопротивления материалов и охватывает цикл из четырех лабораторно-практических работ. Теоретическая часть методического пособия кроме общих сведений содержит примеры по расчету статически неопределимых систем, схемы которых аналогичны лабораторным установкам. Пособие содержит методику проведения лабораторных работ, порядок обработки результатов испытаний и сравнения их с аналитически рассчитанными значениями для оценки адекватности расчетных формул. В приложение к пособию включены необходимые справочные сведения, краткий перечень основных терминов и понятий, карточка тестового контроля. Для подготовки к отчету по данному циклу лабораторно-практических работ приводятся контрольные вопросы и библиографический список.

Утверждено научно-методическим советом Тольяттинского государственного университета

© Тольяттинский государственный университет, 2005

Источник