что такое средняя гармоническая величина
Среднее гармоническое
Предлагаемая здесь программа, помимо расчета среднего гармонического, умеет еще и приводить исходные данные к стандартному виду, а так же упорядочивать их по возрастанию или убыванию.
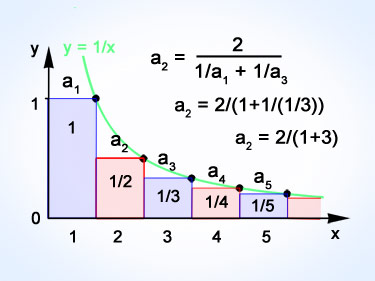
Рис.1. Гармонический ряд и среднее гармоническое
Среднее гармоническое от двух реже трех чисел используется в математике не менее двух с половиной тысяч лет (возможно более 4000 лет). Свойства средних гармонических, арифметических и геометрических величин для двух чисел были детально изучены еще пифагорейцами, поэтому они так же называются классическими пифагорейскими средними.
Свое название среднее гармоническое получило благодаря замечательному свойству гармонического ряда: каждый член ряда, начиная со второго, представляет собой среднее обратно-пропорциональное от двух соседних членов (рисунок). Это свойство гармонического ряда было известно еще во времена Аристотеля.
.
В свете современных представлений:
Среднее гармоническое значение множества положительных вещественных чисел определяется как результат деления количества этих чисел на сумму их обратных величин:
Среднее степенное значение sd порядка (степени) d от множества заданных чисел a 1 + a 2 + …+ a n определяется формулой:
8.3. Средние величины в статистике
Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, являются средние показатели (средняя величина).
Средняя величина – представляет обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.
Показатель в форме средней величины выражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. Он отражает уровень этого признака, отнесенный к единице совокупности.
Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности.
Значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные.
Сущность средней заключается, в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.
ВИДЫ СРЕДНИХ ВЕЛИЧИН наиболее часто применяемых на практике:
Выбор средней величины зависит от содержания осредняемого признака и конкретных данных, по которым ее приходится вычислять.
ФОРМУЛЫ СРЕДНИХ ВЕЛИЧИН
Таблица 8.2 – Результаты опроса работников офиса
Гармоническое Среднее
Что такое Гармоническое Среднее?
Гармоническое среднее – это разновидность среднего численного значения. Он рассчитывается путем деления количества наблюдений на обратную величину каждого числа в серии. Таким образом, гармоническое среднее является величиной, обратной среднему арифметическому обратных величин.
Среднее гармоническое значение 1, 4 и 4 равно:
Краткая справка
Обратное значение числа n равно 1 / n.
Основы гармонического среднего
Гармоническое среднее помогает найти мультипликативные отношения или отношения делителей между дробями, не беспокоясь об общих знаменателях. Гармонические средние часто используются для усреднения таких вещей, как скорости (например, средняя скорость движения при продолжительности нескольких поездок).
Средневзвешенное гармоническое среднее используется в финансах для усреднения мультипликаторов, таких как соотношение цены и прибыли, поскольку оно придает одинаковый вес каждой точке данных. Использование взвешенного среднего арифметического для усреднения этих соотношений даст больший вес высоким точкам данных, чем низким точкам данных, потому что соотношение цена / прибыль не нормализуется по цене, в то время как прибыль выравнивается.
Ключевые моменты
Сравнение среднего гармонического и среднего арифметического и среднего геометрического
Другие способы вычисления средних значений включают простое среднее арифметическое и среднее геометрическое. Среднее арифметическое – это сумма серии чисел, деленная на количество этой серии чисел. Если бы вас попросили найти среднее (арифметическое) среднее количество баллов за тест, вы просто сложите все баллы учащихся, а затем разделите эту сумму на количество учащихся. Например, если пять студентов сдали экзамен и их баллы составили 60%, 70%, 80%, 90% и 100%, средняя арифметическая оценка по классу будет 80%.
Среднее геометрическое среднее из набора продуктов, расчет которых обычно используется для определения результатов эффективности инвестиций или портфеля. Технически это определяется как «произведение корня n-й степени из n чисел». Среднее геометрическое должно использоваться при работе с процентами, которые выводятся из значений, в то время как стандартное среднее арифметическое работает с самими значениями.
Гармоническое среднее лучше всего использовать для таких дробей, как ставки или кратные.
Пример среднего гармонического
В качестве примера возьмем две фирмы. Один имеет рыночную капитализацию 100 миллиардов долларов и прибыль 4 миллиарда долларов (P / E 25), а другой – рыночную капитализацию 1 миллиард долларов и прибыль 4 миллиона долларов (P / E 250). В индексе, составленном из двух акций, с 10% инвестиций в первую и 90% во вторую, коэффициент P / E индекса равен:
Средние величины в статистике
6.2. Средняя гармоническая
Средняя гармоническая величина является модифицированной формой средней арифметической. Она применяется в тех случаях, когда неизвестны значения частот у вариант ряда, зато имеются для каждого xi произведения этих вариант на соответствующие им частоты, т.д.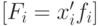 
. Величиной Fi может быть, например, товарооборот по видам товаров при расчете их средней цены; фонд заработной платы по отдельным категориям работников при расчете средней заработной платы и т.д. Ситуаций, когда нам известны не частоты, а произведения частот на соответствующие им варианты при расчете средней величины, более чем достаточно.
Формула средней гармонической взвешенной имеет следующий вид:
Если мы для каждой варианты рассчитаем частоту как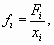 
то формула средней гармонической взвешенной превратится в формулу для расчета средней арифметической взвешенной:
Пример 6.5. Вернемся к примеру 6.2, где рассчитывалась средняя заработная плата 20 работников малого предприятия. Предположим, что изначально были известны данные об уровне заработной платы для каждой группы работающих и начисленный им фонд заработной платы. Тогда для расчета средней заработной платы необходимо определить численность работающих в каждой группе. Для этого разделим фонд заработной платы каждой группы работающих на их уровень заработной платы (см. графу 3 в таблице). Тогда, разделив общий фонд заработной платы на общую численность работающих, получим их среднюю заработную плату.
| Исходные данные | Расчетный показатель | |
|---|---|---|
| заработная плата, руб. | фонд заработной платы, руб. | численность работающих, чел. |
| 1 | 2 | 3 |
| xi | Fi | Fi / xi |
| 5 950 | 35 760 | 6 |
| 6 790 | 54 320 | 8 |
| 7 000 | 42 000 | 6 |
| Итого | 132 080 | 20 |
Как видим, и в первом, и во втором случае расчет производился по одной и той же логической формуле
но использовались разные формулы для расчета, поскольку отличались исходные данные.
Поясним расчет. Мы знаем, что логическая формула для расчета средней цены приобретения одной акции такова:
Однако неизвестно, сколько было куплено акций каждого вида. Поэтому средняя арифметическая здесь не может быть использована.
Кроме того, мы знаем, что на покупку каждого вида акций была выделена одна и та же сумма. Обозначим ее через С. Тогда общая сумма, выделенная на покупку двух видов акций, будет равна 2С, а количество купленных акций каждого вида можно рассчитать следующим образом:
Если подставить эти значения в логическую формулу, то неизвестная величина С (сумма, выделенная на приобретение каждого вида акций) сократится, и расчет действительно будет проведен по формуле средней гармонической простой:
6.3. Средняя геометрическая
Для расчета среднего коэффициента или темпа роста статистического показателя используется формула средней геометрической.
Для несгруппированных данных (при отсутствии частот) или для сгруппированных данных с равными частотами применяется средняя геометрическая простая
Для сгруппированных данных с неравными частотами применяется средняя геометрическая взвешенная
Примеры расчета средней геометрической будут рассмотрены в гл. 9.
6.4. Средняя квадратическая и другие степенные средние
Если подставить в формулу средней степенной m = 2, то получим среднюю квадратическую:
взвешенную (для сгруппированных данных):
простую (для несгруппированных данных):
Средняя квадратическая величина широко применяется при оценке вариации признака, при изучении взаимосвязи явлений. Кроме того, прикладное значение имеет расчет степенных средних и более высоких порядков, например при изучении характеристик распределения случайных величин. Формулы для их вычисления получаются при подстановке в качестве m соответствующего показателя степени.
Правило мажорантности степенных средних состоит в том, что при расчете по одним и тем же данным между числовыми значениями средних, исчисленных по разным формулам, всегда сохраняется следующее неравенство:
Средние величины и показатели вариации
Понятие и виды средних величин
Существует 2 класса средних величин: степенные и структурные.
К структурным средним относятся мода и медиана, но наиболее часто применяются степенные средние различных видов.
Степенные средние величины
Степенные средние могут быть простыми и взвешенными.
Простая средняя величина рассчитывается при наличии двух и более несгруппированных статистических величин, расположенных в произвольном порядке по следующей общей формуле:
Взвешенная средняя величина рассчитывается по сгруппированным статистическим величинам с использованием следующей общей формулы:
Используя общие формулы простой и взвешенной средних при разных показателях степени m, получаем частные формулы каждого вида, которые будут далее подробно рассмотрены.
Средняя арифметическая
Например, студент сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Рассчитаем средний балл по формуле средней арифметической простой: (3+4+4+5)/4 = 16/4 = 4.
Средняя арифметическая взвешенная имеет следующий вид:
Например, студент сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Рассчитаем средний балл по формуле средней арифметической взвешенной: (3*1 + 4*2 + 5*1)/4 = 16/4 = 4.
Если значения X заданы в виде интервалов, то для расчетов используют середины интервалов X, которые определяются как полусумма верхней и нижней границ интервала. А если у интервала X отсутствует нижняя или верхняя граница (открытый интервал), то для ее нахождения применяют размах (разность между верхней и нижней границей) соседнего интервала X.
Средняя арифметическая применяется чаще всего, но бывают случаи, когда необходимо применение других видов средних величин. Рассмотрим такие случаи далее.
Средняя гармоническая
Средняя гармоническая применяется, когда исходные данные не содержат частот f по отдельным значениям X, а представлены как их произведение Xf. Обозначив Xf=w, выразим f=w/X, и, подставив эти обозначения в формулу средней арифметической взвешенной, получим формулу средней гармонической взвешенной:
Таким образом, средняя гармоническая взвешенная применяется тогда, когда неизвестны частоты f, а известно w=Xf. В тех случаях, когда все w=1, то есть индивидуальные значения X встречаются по 1 разу, применяется формула средней гармонической простой:
Средняя геометрическая
Средняя геометрическая применяется при определении средних относительных изменений, о чем сказано в теме Ряды динамики. Геометрическая средняя величина дает наиболее точный результат осреднения, если задача стоит в нахождении такого значения X, который был бы равноудален как от максимального, так и от минимального значения X.
Средняя квадратическая
Средняя квадратическая применяется в тех случая, когда исходные значения X могут быть как положительными, так и отрицательными, например при расчете средних отклонений.
Главной сферой применения квадратической средней является измерение вариации значений X, о чем пойдет речь позднее в этой лекции.
Средняя кубическая
Средняя кубическая применяется крайне редко, например, при расчете индексов нищеты населения для развивающихся стран (ИНН-1) и для развитых (ИНН-2), предложенных и рассчитываемых ООН.
Структурные средние величины
К наиболее часто используемым структурным средним относятся статистическая мода и статистическая медиана.
Статистическая мода
Если X задан дискретно, то мода определяется без вычисления как значение признака с наибольшей частотой. В статистической совокупности бывает 2 и более моды, тогда она считается бимодальной (если моды две) или мультимодальной (если мод более двух), и это свидетельствует о неоднородности совокупности.
Если X задан равными интервалами, то сначала определяется модальный интервал как интервал с наибольшей частотой f. Внутри этого интервала находят условное значение моды по формуле:
где Мо – мода;
ХНМо – нижняя граница модального интервала;
hМо – размах модального интервала (разность между его верхней и нижней границей);
fМо – частота модального интервала;
fМо-1 – частота интервала, предшествующего модальному;
fМо+1 – частота интервала, следующего за модальным.
Если размах интервалов h разный, то вместо частот f необходимо использовать плотности интервалов, рассчитываемые путем деления частот f на размах интервала h.
Статистическая медиана
Если X задан дискретно, то для определения медианы все значения нумеруются от 0 до N в порядке возрастания, тогда медиана при четном числе N будет лежать посередине между X c номерами 0,5N и (0,5N+1), а при нечетном числе N будет соответствовать значению X с номером 0,5(N+1).
Если X задан в виде равных интервалов, то сначала определяется медианный интервал (интервал, в котором заканчивается одна половина частот f и начинается другая половина), в котором находят условное значение медианы по формуле:
где Ме – медиана;
ХНМе – нижняя граница медианного интервала;
hМе – размах медианного интервала (разность между его верхней и нижней границей);
fМе – частота медианного интервала; 
fМе-1 – сумма частот интервалов, предшествующих медианному.
Также как и в случае с модой, при определении медианы если размах интервалов h разный, то вместо частот f необходимо использовать плотности интервалов, рассчитываемые путем деления частот f на размах интервала h.
Показатели вариации
Размах вариации
Размах вариации – это разность между максимальным и минимальным значениями X из имеющихся в изучаемой статистической совокупности:
Недостатком показателя H является то, что он показывает только максимальное различие значений X и не может измерять силу вариации во всей совокупности.
Cреднее линейное отклонение
Например, студент сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Ранее уже была рассчитана средняя арифметическая = 4. Рассчитаем среднее линейное отклонение простое: Л = (|3-4|+|4-4|+|4-4|+|5-4|)/4 = 0,5.
Вернемся к примеру про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Ранее уже была рассчитана средняя арифметическая = 4 и среднее линейное отклонение простое = 0,5. Рассчитаем среднее линейное отклонение взвешенное: Л = (|3-4|*1+|4-4|*2+|5-4|*1)/4 = 0,5.
Линейный коэффициент вариации
С помощью линейного коэффициента вариации можно сравнивать вариацию разных совокупностей, потому что в отличие от среднего линейного отклонения его значение не зависит от единиц измерения X.
В рассматриваемом примере про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5, линейный коэффициент вариации составит 0,5/4 = 0,125 или 12,5%.
Дисперсия
В уже знакомом нам примере про студента, который сдал 4 экзамена и получил оценки: 3, 4, 4 и 5, ранее уже была рассчитана средняя арифметическая = 4. Тогда дисперсия простая Д = ((3-4) 2 +(4-4) 2 +(4-4) 2 +(5-4) 2 )/4 = 0,5.
В рассматриваемом примере про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5, рассчитаем дисперсию взвешенную: Д = ((3-4) 2 *1+(4-4) 2 *2+(5-4) 2 *1)/4 = 0,5.
Если преобразовать формулу дисперсии (раскрыть скобки в числителе, почленно разделить на знаменатель и привести подобные), то можно получить еще одну формулу для ее расчета как разность средней квадратов и квадрата средней:
В уже знакомом нам примере про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5, рассчитаем дисперсию методом разности средней квадратов и квадрата средней:
Д = (3 2 *1+4 2 *2+5 2 *1)/4-4 2 = 16,5-16 = 0,5.
.
Cреднее квадратическое отклонение
Выше уже было рассказано о формуле средней квадратической, которая применяется для оценки вариации путем расчета среднего квадратического отклонения, обозначаемое малой греческой буквой сигма:
Еще проще можно найти среднее квадратическое отклонение, если предварительно рассчитана дисперсия, как корень квадратный из нее:
В примере про студента, в котором выше рассчитали дисперсию, найдем среднее квадратическое отклонение как корень квадратный из нее:
.
.Квадратический коэффициент вариации
В примере про студента, в котором выше рассчитали среднее квадратическое отклонение, найдем квадратический коэффициент вариации V = 0,707/4 = 0,177, что меньше критериального значения 0,333, значит вариация слабая и равна 17,7%.
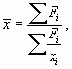
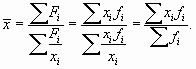
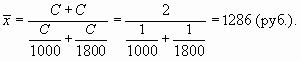
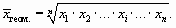
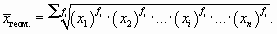
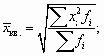