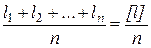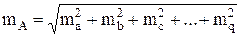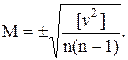что такое среднеквадратическая ошибка

Средняя квадратичная ошибка

Оценка точности результатов измерений

Оценить точность каких-либо измерений – это значит определить на основе полученных результатов сравнимые числовые (количественные) характеристики, выражающие качественную сторону самих измерений и условий их проведения. Количественные характеристики измерений или критерии оценки точности измерений устанавливаются теорией вероятности и теорией ошибок (в частности, способом наименьших квадратов). Согласно этим теориям оценка точности результатов измерений производится только по случайным ошибкам.

Показателями точности измерений могут служить:

— средняя квадратическая ошибка измерений;

— относительная ошибка измерений;

— предельная ошибка измерений.

Понятие средней квадратичной ошибки введено Гауссом, и в настоящее время она принята в качестве основной характеристики точности измерений в геодезии.

Средней квадратичной ошибкой называется среднее квадратичное значение из суммы квадратов ошибок отдельных измерений. Для ее вычисления используют либо истинные ошибки измерений, либо уклонения результатов измерений от среднего арифметического.

Обозначим истинное значение измеряемой величины через X, результат измерения через l_i.

Истинными ошибками измерений Δ_i называются разности результатов измерений и истинных значений, т. е.

В этом случае среднюю квадратичную ошибку m отдельного результата вычисляют по формуле:

(11)

где n – количество равноточных измерений.

Однако в большинстве случаев практики, если не считать редких случаев специальных исследований, истинное значение измеряемой величины и, следовательно, истинные ошибки остаются неизвестными. В этих случаях для нахождения окончательного значения измеряемой величины и оценки точности результатов измерений используют принцип среднего арифметического.

называется средним арифметическим из измеренных значений этой величины.

Разность каждого отдельного результата измерения и среднего арифметического значения называется уклонением результатов измерений от среднего арифметического и обозначается буквой v:

v_i = l_i – .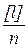

Пример. Отдельный угол измерен четырьмя приемами, и получены результаты:

Уклонения результатов измерений от среднего арифметического обладают двумя важными свойствами:

— для любого ряда равноточных измерений алгебраическая сумма уклонений равна нулю [v] = 0;

— для любого ряда равноточных измерений сумма квадратов уклонений минимальна, т. е. меньше суммы квадратов уклонений отдельных измерений от любого другого значения, принятого, вместо среднего арифметического значения, [v 2 ] = min.

Первое свойство уклонений служит надежным контролем вычисления среднего арифметического значения из результатов измерений. Второе свойство уклонений используют для оценки точности результатов измерений.

Если ошибки отдельных измерений вычисляют относительно среднего арифметического значения из результатов измерений, среднюю квадратичную ошибку отдельного результата вычисляют по формуле

. (12)

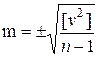
Пример. Используя данные предыдущего примера, найдем среднюю квадратичную ошибку измерения угла одним приемом:

.

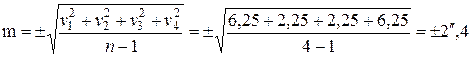
При определении средних квадратичных ошибок измерений необходимо руководствоваться следующими правилами:

;

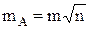
2) средняя квадратичная ошибка произведения измеренной величины на постоянное число равна произведению средней квадратичной ошибки этой величины на то же самое число, т. е. для выражения L = kl;

;

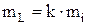
3) средняя квадратичная ошибка результатов равноточных измерений прямо пропорциональна средней квадратичной ошибке одного измерения m и обратно пропорциональна корню квадратному из числа измерений, т.е.

;

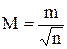
или с учетом формулы (12):

Примеры: 1. Угол β получен как разность двух направлений, определенных с ошибками m₁ = ± 3″ и m₂ = ± 4″.

По первому правилу находим .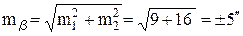

2. Радиус окружности измерен со средней квадратичной ошибкой m_R = ±5 см.

По второму правилу находим среднюю квадратичную ошибку длины окружности

m₀ = 2πm_R = 2 × 3,14 × 5 = ± 31 см.

3. Средняя квадратичная ошибка измерения угла одним приемом равно m = ± 8″. Какова точность измерения угла четырьмя приемами?

По третьему правилу

.

Источник

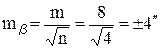
Среднеквадратическая ошибка (MSE)

Среднеквадратичная ошибка (Mean Squared Error) – Среднее арифметическое (Mean) квадратов разностей между предсказанными и реальными значениями Модели (Model) Машинного обучения (ML):

MSE как среднее дистанций между предсказаниями и реальными наблюдениями

Рассчитывается с помощью формулы, которая будет пояснена в примере ниже:

MSE практически никогда не равен нулю, и происходит это из-за элемента случайности в данных или неучитывания Оценочной функцией (Estimator) всех факторов, которые могли бы улучшить предсказательную способность.

Пример. Исследуем линейную регрессию, изображенную на графике выше, и установим величину среднеквадратической Ошибки (Error). Фактические координаты точек-Наблюдений (Observation) выглядят следующим образом:

Мы имеем дело с Линейной регрессией (Linear Regression), потому уравнение, предсказывающее положение записей, можно представить с помощью формулы:

Параметры M и b уравнения нам, к счастью, известны в данном обучающем примере, и потому уравнение выглядит следующим образом:

$$y = 0,5252 * x + 17,306$$

Зная координаты реальных записей и уравнение линейной регрессии, мы можем восстановить полные координаты предсказанных наблюдений, обозначенных серыми точками на графике выше. Простой подстановкой значения координаты x в уравнение мы рассчитаем значение координаты ỹ:

Рассчитаем квадрат разницы между Y и Ỹ:

Сумма таких квадратов равна 4 445. Осталось только разделить это число на количество наблюдений (9):

$$MSE = \frac<1> <9>× 4445 = 493$$

Само по себе число в такой ситуации становится показательным, когда Дата-сайентист (Data Scientist) предпринимает попытки улучшить предсказательную способность модели и сравнивает MSE каждой итерации, выбирая такое уравнение, что сгенерирует наименьшую погрешность в предсказаниях.

MSE и Scikit-learn

Среднеквадратическую ошибку можно вычислить с помощью SkLearn. Для начала импортируем функцию:

Инициализируем крошечные списки, содержащие реальные и предсказанные координаты y:

Интересно, что конечный результат на 3 отличается от расчетов с помощью Apple Numbers:

Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.

Источник

Тема: Элементы теории ошибок измерений.

1. Классификация ошибок измерений

_______ Измерения в геодезии рассматриваются с двух точек зрения: количественной, выражающей числовое значение измеренной величины, и качественной, характеризующей ее точность. Из практики известно, что даже при самой тщательной и аккуратной работе многократные (повторные) измерения не дают одинаковых результатов. Это указывает на то, что получаемые результаты не являются точным значением измеряемой величины, а несколько отклоняются от него. Значение отклонения характеризует точность измерений.

_______ К грубым ошибкам относятся просчеты в измерениях по причине невнимательности наблюдателя или неисправности прибора, и они полностью должны быть исключены. Это достигается путем повторного измерения.

_______ Систематические ошибки происходят от известного источника, имеют определенный знак и величину и их можно учесть при измерениях и вычислениях.

_______ Случайные ошибки обусловлены разными причинами и полностью исключить их из измерений нельзя. Поэтому возникают две задачи: как из результатов измерений получить наиболее точную величину и как оценить точность полученных результатов измерений. Эти задачи решаются с помощью теории ошибок измерений _______

_______ В основу теории ошибок положены следующие свойства случайных ошибок :
_______ 1. Малые ошибки встречаются чаще, а большие реже.
_______ 2. Ошибки не превышают известного предела.
_______ 3. Положительные и отрицательные ошибки, одинаковые по абсолютной величине, одинаково часто встречаются.
_______ 4. Сумма ошибок, деленная на число измерений, стремится к нулю при большом числе измерений.

_______ По источнику происхождения различают ошибки приборов, внешние и личные. Ошибки приборов обусловлены их несовершенством, например погрешность угла, измеренного теодолитом, неточным приведением в вертикальное положение оси его вращения.

_______ Внешние ошибки происходят из-за влияния внешней среды, в которой протекают измерения, например погрешность в отсчете по нивелирной рейке из-за изменения температуры воздуха на пути светового луча (рефракция) или нагрева нивелира солнечными лучами.

_______ Личные ошибки связаны с особенностями наблюдателя, например, разные наблюдатели по-разному наводят зрительную трубу на визирную цель. Так как грубые погрешности должны быть исключены из результатов измерений, а систематические исключены или ослаблены до минимально допустимого предела, то проектирование измерений с необходимой точностью и оценку результатов выполненных измерений производят, основываясь на свойствах случайных погрешностей.

2. Арифметическая середина

_______ Величина x называется арифметической серединой или вероятнейшим значением измеренной величины. Разности между каждым измерением и арифметической срединой называют вероятнейшими ошибками измерений:

_______ Или в общем виде получим:

3. Средняя квадратическая ошибка

_______ Точность результатов измерений оценивается средней квадратической ошибкой. Средняя квадратическая ошибка одного измерения вычисляется по формуле:

где [v 2 ] – сумма квадратов вероятнейших ошибок; n – число измерений. Средняя квадратическая ошибка арифметической середины вычисляется по формуле:

_______ Предельная ошибка не должна превышать утроенной средней квадратической ошибки, т.е. ε = 3 x m.

_______ Иногда о точности измерений судят не по абсолютной величине средней квадратической или предельной погрешности, а по величине относительной ошибки. ___

_______ Относительной ошибкой называется отношение абсолютной ошибки к значению самой измеренной величины. Относительную ошибку выражают в виде простой дроби, числитель которой — единица, а знаменатель — число, округленное до двух-трех значащих цифр с нулями. Например, относительная средняя квадратическая погрешность измерения линии длиной:

_______ l = 110 м, при m = 2 см, равна m/ l = 1/5500.

_______ Линия измерена шесть раз. Определить ее вероятнейшую длину и оценить точность этого результата. Вычисления приведены в таблице:

Таб. 1

_______ По формулам вычислены абсолютные средние квадратические ошибки, а оценивать точность измерения длины линии необходимо по относительной ошибке. Поэтому нужно абсолютную ошибку разделить на длину линии. Для нашего примера относительная ошибка вероятнейшего значения измеренной линии равна

4. Оценка точности измерений

_______ Точность результатов многократных измерений одной и той же величины оценивают в такой последовательности:

_______ 1. Находят вероятнейшее (наиболее точное для данных условий) значение измеренной величины по формуле арифметической середины х = [ l ]/n.
_______ 2. Вычисляют отклонения для каждого значения измеренной величины от значения арифметической средины. Контроль вычислений: [v] = 0;
_______ 3. По формуле вычисляют среднюю квадратическую ошибку одного измерения.
_______ 4. По формуле вычисляют среднюю квадратическую ошибку арифметической средины.
_______ 5. Если измеряют линейную величину, то подсчитывают относительную среднюю квадратическую ошибку каждого измерения и арифметической средины.

_______ 6. При необходимости подсчитывают предельную ошибку одного измерения, которая может служить допустимым значением погрешностей аналогичных измерений.

5. Понятие о неравноточных измерениях

_______ Неравноточными измерениями называются такие, которые выполнены различным числом приемов, приборами различной точности и т.д. Если измерения неодинаковой точности, то для определения общей арифметической середины пользуются формулой:

________ Весом называется число, которое выражает степень доверия к результату измерения. В тех случаях, когда неизвестны веса измеренных величин, а известны их средние квадратические ошибки, то веса можно вычислить по формуле:

т.е. вес результата измерений обратно пропорционален квадрату средней квадратической ошибки.

_______ При неравноточных измерениях средняя квадратическая ошибка измерения, вес которого равен единице, определяется по формуле:

где δ – разность между отдельными результатами измерений и общей арифметической серединой.

Источник

Среднеквадратическая ошибка

В теории вероятностей и статистике среднеквадрати́ческое (среднеквадрати́чное) отклоне́ние — наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания (аналога среднего арифметического с бесконечным числом исходов). Обычно он означает квадратный корень из дисперсии случайной величины, но иногда может означать тот или иной вариант оценки этого значения.

Содержание

Термин [ | ]

Встречаются также синонимы словосочетания среднеквадрати́ческое отклоне́ние, как то́:

Основные сведения [ | ]

Среднеквадратическое отклонение определяется как квадратный корень из дисперсии случайной величины: σ = D [ X ] <\displaystyle \sigma =<\sqrt >> .

Среднеквадратическое отклонение измеряется в единицах измерения самой случайной величины и используется при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами.

На практике, когда вместо точного распределения случайной величины в распоряжении имеется лишь выборка, стандартное отклонение, как и математическое ожидание, оценивают (выборочная дисперсия), и делать это можно разными способами. Термины «стандартное отклонение» и «среднеквадратическое отклонение» обычно применяют к квадратному корню из дисперсии случайной величины (определённому через её истинное распределение), но иногда и к различным вариантам оценки этой величины на основании выборки.

то два основных способа оценки стандартного отклонения записываются нижеследующим образом.

Оценка стандартного отклонения на основании смещённой оценки дисперсии (иногда называемой просто выборочной дисперсией [1] ):

Это в буквальном смысле среднее квадратическое разностей измеренных значений и среднего.

Само по себе, однако, S 0 <\displaystyle S_<0>> не является несмещённой оценкой квадратного корня из дисперсии, то есть извлечение квадратного корня «портит» несмещённость.

Среднеквадратичное отклонение среднего [ | ]

Среднее значение выборки также является случайной величиной с оценкой среднеквадратичного отклонения [2] [ нет в источнике ]

Правило трёх сигм [ | ]

Интерпретация величины среднеквадратического отклонения [ | ]

Большее значение среднеквадратического отклонения показывает больший разброс значений в представленном множестве со средней величиной множества; меньшее значение, соответственно, показывает, что значения в множестве сгруппированы вокруг среднего значения.

Например, у нас есть три числовых множества: <0, 0, 14, 14>, <0, 6, 8, 14>и <6, 6, 8, 8>. У всех трёх множеств средние значения равны 7, а среднеквадратические отклонения, соответственно, равны 7, 5 и 1. У последнего множества среднеквадратическое отклонение маленькое, так как значения в множестве сгруппированы вокруг среднего значения; у первого множества самое большое значение среднеквадратического отклонения — значения внутри множества сильно расходятся со средним значением.

В общем смысле среднеквадратическое отклонение можно считать мерой неопределённости. К примеру, в физике среднеквадратическое отклонение используется для определения погрешности серии последовательных измерений какой-либо величины. Это значение очень важно для определения правдоподобности изучаемого явления в сравнении с предсказанным теорией значением: если среднее значение измерений сильно отличается от предсказанных теорией значений (большое значение среднеквадратического отклонения), то полученные значения или метод их получения следует перепроверить.

Практическое применение [ | ]

На практике среднеквадратическое отклонение позволяет оценить, насколько значения из множества могут отличаться от среднего значения.

Экономика и финансы [ | ]

Среднее квадратическое отклонение доходности портфеля σ = D [ X ] <\displaystyle \sigma =<\sqrt >> отождествляется с риском портфеля.

В техническом анализе среднеквадратическое отклонение используется для построения линий Боллинджера, расчёта волатильности.

Климат [ | ]

Предположим, существуют два города с одинаковой средней максимальной дневной температурой, но один расположен на побережье, а другой внутри континента. Известно, что в городах, расположенных на побережье, множество различных максимальных дневных температур меньше, чем у городов, расположенных внутри континента. Поэтому среднеквадратическое отклонение максимальных дневных температур у прибрежного города будет меньше, чем у второго города, несмотря на то, что среднее значение этой величины у них одинаковое, что на практике означает, что вероятность того, что максимальная температура воздуха каждого конкретного дня в году будет сильнее отличаться от среднего значения, выше у города, расположенного внутри континента.

Спорт [ | ]

Предположим, что есть несколько футбольных команд, которые оцениваются по некоторому набору параметров, например, количеству забитых и пропущенных голов, голевых моментов и т. п. Наиболее вероятно, что лучшая в этой группе команда будет иметь лучшие значения по большему количеству параметров. Чем меньше у команды среднеквадратическое отклонение по каждому из представленных параметров, тем предсказуемее является результат команды, такие команды являются сбалансированными. С другой стороны, у команды с большим значением среднеквадратического отклонения сложно предсказать результат, что в свою очередь объясняется дисбалансом, например, сильной защитой, но слабым нападением.

Использование среднеквадратического отклонения параметров команды позволяет в той или иной мере предсказать результат матча двух команд, оценивая сильные и слабые стороны команд, а значит, и выбираемых способов борьбы.

Пример вычисления стандартного отклонения оценок учеников [ | ]

Предположим, что интересующая нас группа (генеральная совокупность) это класс из восьми учеников, которым выставляются оценки по 10-бальной системе. Так как мы оцениваем всю группу, а не её выборку, можно использовать стандартное отклонение на основании смещённой оценки дисперсии. Для этого берём квадратный корень из среднего арифметического квадратов отклонений величин от их среднего значения.

Пусть оценки учеников класса следующие:

Тогда средняя оценка равна:

μ = 2 + 4 + 4 + 4 + 5 + 5 + 7 + 9 8 = 5 <\displaystyle \mu =<\frac <2+4+4+4+5+5+7+9><8>>=5>

Вычислим квадраты отклонений оценок учеников от их средней оценки:

( 2 − 5 ) 2 = ( − 3 ) 2 = 9 ( 5 − 5 ) 2 = 0 2 = 0 ( 4 − 5 ) 2 = ( − 1 ) 2 = 1 ( 5 − 5 ) 2 = 0 2 = 0 ( 4 − 5 ) 2 = ( − 1 ) 2 = 1 ( 7 − 5 ) 2 = 2 2 = 4 ( 4 − 5 ) 2 = ( − 1 ) 2 = 1 ( 9 − 5 ) 2 = 4 2 = 16 <\displaystyle <\begin(2-5)^<2>=(-3)^<2>=9&&(5-5)^<2>=0^<2>=0\\(4-5)^<2>=(-1)^<2>=1&&(5-5)^<2>=0^<2>=0\\(4-5)^<2>=(-1)^<2>=1&&(7-5)^<2>=2^<2>=4\\(4-5)^<2>=(-1)^<2>=1&&(9-5)^<2>=4^<2>=16\\\end>>

Среднее арифметическое этих значений называется дисперсией:

σ 2 = 9 + 1 + 1 + 1 + 0 + 0 + 4 + 16 8 = 4 <\displaystyle \sigma ^<2>=<\frac <9+1+1+1+0+0+4+16><8>>=4>

Стандартное отклонение равно квадратному корню дисперсии:

Эта формула справедлива только если эти восемь значений и являются генеральной совокупностью. Если бы эти данные были случайной выборкой из какой-то большой совокупности (например, оценки восьми случайно выбранных учеников большого города), то в знаменателе формулы для вычисления дисперсии вместо n = 8 нужно было бы поставить n − 1 = 7:

и стандартное отклонение равнялось бы:

Этот результат называется стандартным отклонением на основании несмещённой оценки дисперсии. Деление на n − 1 вместо n даёт неискажённую оценку дисперсии для больших генеральных совокупностей.

Источник