Сравнение чисел по модулю
Определение 1. Если два числа 1 ) a и b при делении на p дают один и тот же остаток r, то такие числа называются равноостаточными или сравнимыми по модулю p.
Утверждение 1. Пусть p какое нибудь положительное число. Тогда всякое число a всегда и притом единственным способом может быть представлено в виде
1 ) В данной статье под словом число будем понимать целое число.
Действительно. Если s получит значение от −∞ до +∞, то числа sp представляют собой совокупность всех чисел, кратных p. Рассмотрим числа между sp и (s+1)p=sp+p. Так как p целое положительное число, то между sp и sp+p находятся числа
  |
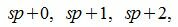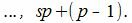Но эти числа можно получить задав r равным 0, 1, 2. p−1. Следовательно sp+r=a получит всевозможные целые значения.
Покажем, что это представление единственно. Предположим, что p можно представить двумя способами a=sp+r и a=s1p+r1. Тогда
 |
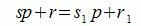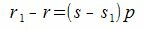 | (2) |
Число r называется вычетом числа a по модулю p (другими словами, число r называется остатком от деления числа a на p).
Утверждение 2. Если два числа a и b сравнимы по модулю p, то a−b делится на p.
Действительно. Если два числа a и b сравнимы по модулю p, то они при делении на p имеют один и тот же остаток p. Тогда
 |
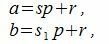где s и s1 некоторые целые числа.
Разность этих чисел
 | (3) |
делится на p, т.к. правая часть уравнения (3) делится на p.
Утверждение 3. Если разность двух чисел делится на p, то эти числа сравнимы по модулю p.
Доказательство. Обозначим через r и r1 остатки от деления a и b на p. Тогда
 |
 |
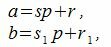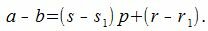По утверждению a−b делится на p. Следовательно r−r1 тоже делится на p. Но т.к. r и r1 числа 0,1. p−1, то абсолютное значение |r−r1| Свойство 1. Для любого a и p всегда
Действительно. Из условия свойства 2 следует a−b и b−c делятся на p. Тогда их сумма a−b+(b−c)=a−c также делится на p.
| a≡b mod (p) и m≡n mod (p), |
| a+m≡b+n mod (p) и a−m≡b−n mod (p). |
Действительно. Так как a−b и m−n делятся на p, то
также делятся на p.
Это свойство можно распространить на какое угодно число сравнений, имеющих один и тот же модуль.
| a≡b mod (p) и m≡n mod (p), |
Действительно.Так как a−b делится на p, то (a−b)m также делится на p, следовательно
Далее m−n делится на p, следовательно b(m−n)=bm−bn также делится на p, значит
Таким образом два числа am и bn сравнимы по модулю с одним и тем же числом bm, следовательно они сравнимы между собой (свойство 2).
где k некоторое неотрицательное целое число.
Действительно. Имеем a≡b mod (p). Из свойства 4 следует
| a·a≡b·b mod (p). |
| a·a·a≡b·b·b mod (p). |
| . |
| a k ≡b k mod (p). |
Все свойства 1-5 представить в следующем утверждении:
При делении все обстоит иначе. Из сравнения
не всегда следует сравнение
Утверждение 5. Пусть
Доказательство. Пусть λ наибольший общий делитель чисел m и p. Тогда
Так как m(a−b) делится на k, то
 |
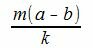имеет нулевой остаток. Тогда
  . |
 |
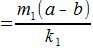имеет нулевой остаток, т.е. m1(a−b) делится на k1. Но числа m1 и k1 числа взаимно простые. Следовательно a−b делится на k1=k/λ и, тогда, a≡b mod (p/λ).
Утверждение 6. Если
и m является один из делителей числа p, то
Действительно. a−b делится на p. p делится на m. Следовательно a−b делится на m.
Утверждение 7. Если
| a≡b mod (p), a≡b mod (q), a≡b mod (s) |
где h наименьшее общее кратное чисел p,q,s.
Действительно. Разность a≡b должна быть числом, кратным p,q,s. и, следовательно должна быть кратным h.
В частном случае, если модули p,q,s взаимно простые числа, то
Заметим, что можно допустить сравнения по отрицательным модулям, т.е. сравнение a≡b mod (p) означает и в этом случае, что разность a−b делится на p. Все свойства сравнений остаются в силе и для отрицательных модулей.
Конспект «теория сравнения по модулю»
Муниципальное бюджетное общеобразовательное учреждение
Семлевская средняя общеобразовательная школа №1
Вяземского района Смоленской области
Научно-исследовательская работа по теме
«Теория сравнения по модулю»
Подготовила
ученица 9 класса: Попова Анастасия
Преподаватель: Перцева С.М.
Понятие модуля числа известно каждому, а вот что означает понятие сравнение по модулю, знают далеко не все. Тема моей работы «Теория сравнения по модулю». Я обратилась к этой теме, так как она недостаточно полно изложена в действующих учебниках математики, а задачи по этой теме предлагаются как на олимпиадах, так и на вступительных экзаменах в вузы.
1) Изучить краткий исторический обзор возникновения теории;
2) Дать определение сравнения по модулю;
3) Изучить свойства сравнения по модулю;
4) Рассмотреть операции со сравнениями;
5) Применить знания для решения практических заданий.
1)Теоретический анализ и обобщение научной литературы;
2)Математический расчет;
Если два целых числа 
и 
при делении на 
дают одинаковые остатки, то они называются сравнимыми по модулю числа .
Сравнимость чисел и записывается в виде формулы ( сравнения ):
Число называется модулем сравнения.
Определение сравнимости чисел и по модулю равносильно любому из следующих утверждений:
Разность чисел и делится на без остатка; 
Число может быть представлено в виде 
, где 
— некоторое целое число.
Например : 32 и −10 сравнимы по модулю 7, так как оба числа при делении на 7 дают остаток 4:
Также, 32 и −10 сравнимы по модулю 7, так как их разность 42 делится на 7, и к тому же имеет место представление:
Сравнения, система вычетов, решение линейных систем по модулю
Содержание
Сравнения по модулю [ править ]
Будем рассматривать целые числа в связи с остатками от деления их на данное целое число m, которое назовем модулем. Каждому целому числу отвечает определенный остаток от деления его на m. Если двум целым a и b отвечает один и тот же остаток r, то они называются сравнимыми по модулю m.
Сравнимость для a и b записывается так :
[math]a \equiv b(mod \text < >m)[/math]
Сравнимость чисел a и b по модулю m равносильна:
Арифметика сравнений [ править ]
Свойства сравнений [ править ]
Полная и приведенная система вычетов [ править ]
Числа равноостаточные(сравнимые по модулю m) образуют класс чисел по модулю m. Из такого определения следует, что всем числам класса отвечает один остаток r, и мы получим все числа класса, если в форме [math]mt + r [/math] заставим t пробегать все целые числа. Таким образом для каждого значения остатка имеется свой класс чисел.
Любые m чисел, попарно несравнимые по модулю m, образуют полную систему вычетов по этому модулю.
Согласно 10 свойству сравнений, числа одного класса по модулю m имеют одинаковый НОД. Особенно важны классы, содержащие числа, взаимно простые с модулем. Взяв вычет от каждого такого класса, получим приведенную систему вычетов по модулю m.