что такое спектральная плотность виброускорения
Лекция 14. Спектральный анализ вибрации
Спектральный анализ – это метод обработки сигналов, который позволяет выявить частотный состав сигнала. Известны методы обработки вибрационного сигнала: корреляционный, автокорреляционный, спектральной мощности, кепстральных характеристик, расчета эксцесса, огибающей. Наибольшее распространение получил спектральный анализ, как метод представления информации, из-за однозначной идентификации повреждений и понятных кинематических зависимостей между происходящими процессами и спектрами вибрации.
Наглядное представление о составе спектра дает графическое изображение вибрационного сигнала в виде спектрограмм. Выявление картины амплитуд, составляющих вибрации позволяет идентифицировать неисправности оборудования. Анализ спектрограмм виброускорения позволяет распознать повреждения на ранней стадии. Спектрограммы виброскорости используются при мониторинге развитых повреждений. Поиск повреждений проводится на заранее определенных частотах возможных повреждений. Для анализа вибрационного спектра, выделяются основные составляющие спектрального сигнала из следующего перечня.
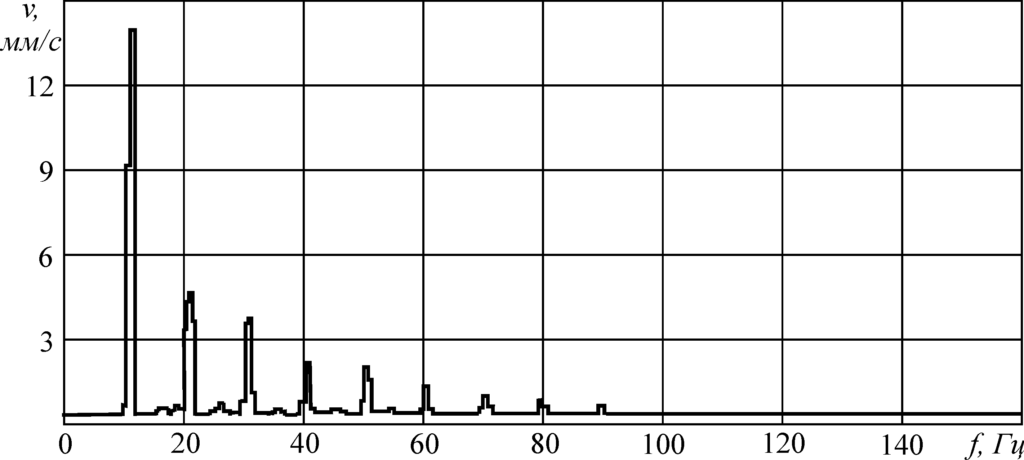
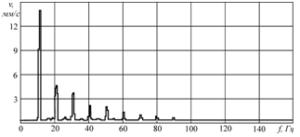
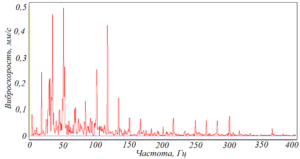
Рисунок 102 – Гармонические составляющие вибрационного сигнала при дисбалансе ротора
Основные причины появления гармоник:
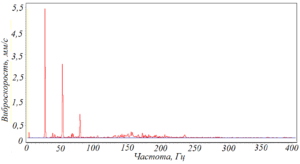
Рисунок 103 – Субгармоника 1/4 оборотной частоты вибрационного сигнала
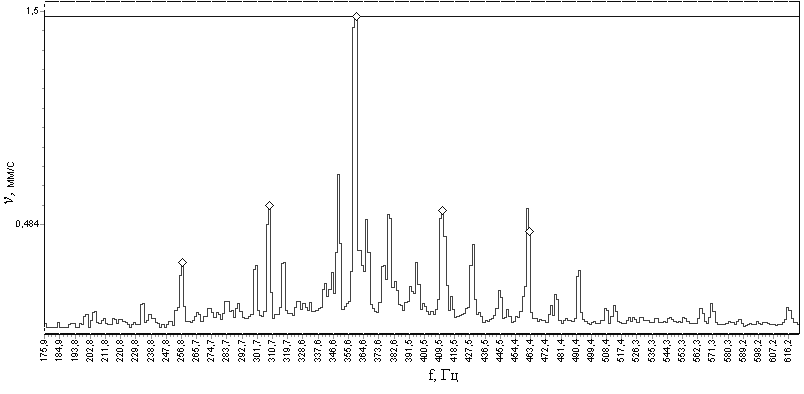
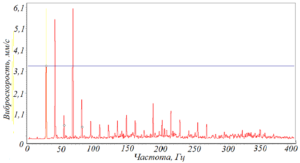
Рисунок 104 – Полуторные гармоники оборотной частоты
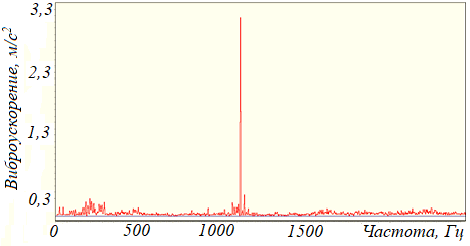
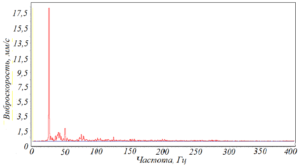
Рисунок 105 – Резонансная составляющая на частоте 1140 Гц
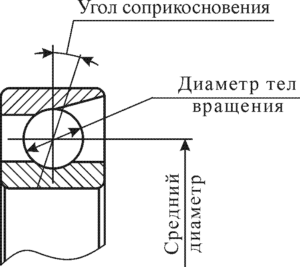
где fвр – частота вращения вала; z число тел качения; d – диаметр тел качения; β – угол контакта (соприкосновения тел качения и беговой дорожки); D – диаметр окружности, проходящей через центры тел качения (рисунок 107).
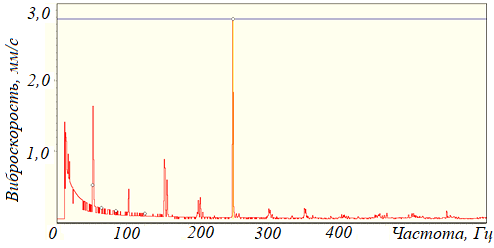
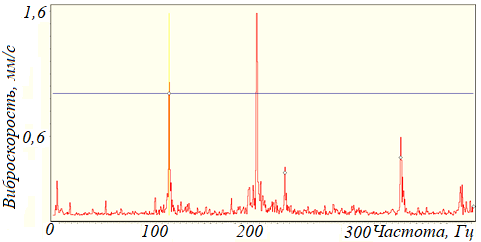
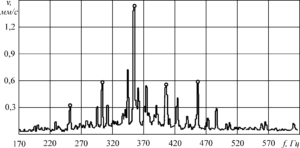
Рисунок 106 – Спектр виброскости подшипника качения с повреждениями наружного кольца – появление гармоник с частотой перекатывания тел качения по наружному кольцу
Рисунок 107 – Схема к расчету частот повреждений подшипников
При значительном развитии повреждения появляются гармонические составляющие. Степень повреждения подшипника определяется числом гармоник определенного повреждения.
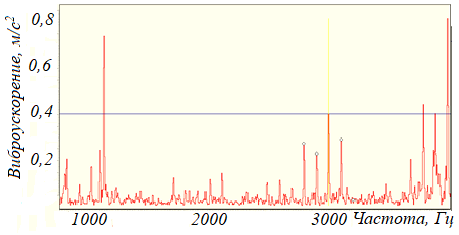
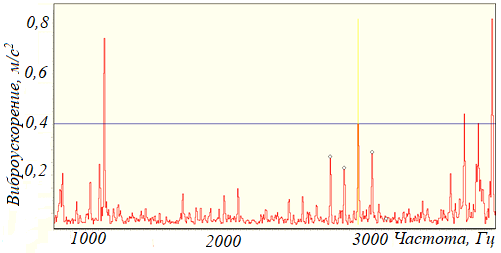
Повреждения подшипников качения приводят к появлению большого количества составляющих в спектре виброускорения в районе собственных частот подшипников 2000…4000 Гц (рисунок 108).
Рисунок 108 – Резонанс тел качения при износе подшипника на частоте 2800…3700 Гц в спектре виброускорения
где z – число зубьев колеса либо число лопаток.
Повреждения, проявляемые на зубцовой частоте, могут генерировать гармонические составляющие при дальнейшем развитии повреждения (рисунок 109).
Рисунок 109 – Зубцовые частоты и негармоническая составляющая повреждений подшипника
Рисунок 110 – Модуляция с частотой 47 Гц зубцовой составляющей на частоте 708 Гц
Рисунок 111 – Модуляции с частотой 100 Гц вибрационного сигнала
Рисунок 112 – Шумовые компоненты в составе вибрационного сигнала
При наличии знаний о составляющих спектра появляется возможность различения их в частотном спектре и определения причин и следствий повреждения (рисунок 113).
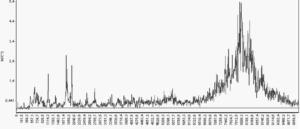
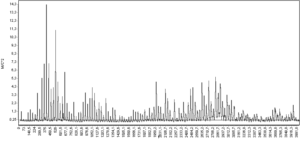
Рисунок 113 – Примеры спектральной формы вибрационного сигнала:
а) спектрограмма виброскорости механизма, имеющего дисбаланс ротора и частоту первой гармоники 10 Гц; б) спектр виброскости подшипника качения с повреждениями наружного кольца – появление гармоник с частотой перекатывания тел качения по наружному кольцу; в) спектрограмма виброускорения соответствующая повреждениям подшипников качения шпинделя вертикально-фрезерного станка – резонансные составляющие на частотах 7000…9500 Гц; г) спектрограмма виброускорения при схватывании второго рода, детали обрабатываемой на металлорежущем станке
Правила анализа спектральных составляющих
Для эффективного мониторинга технического состояния необходим ежеме-сячный контроль спектрального анализа составляющих виброскорости. В истории развития повреждений существует несколько этапов:
Рисунок 114 – Этапы развития повреждений механизма – виткоукладчика:
а) хорошее состояние; б) начальная неуравновешенность; в) средний уровень повреждений; г) значительные повреждения
Одним из характерных повреждений механизма после длительной эксплуатации (10…15 лет) является непараллельность опорных поверхностей корпуса машины и фундамента, при этом вес машины распределяется на три или две опоры. Спектр виброскорости в этом случае содержит гармонические составляющие с амплитудой более 4,5 мм/с и полуторные гармоники. Повреждение приводит к повышенной податливости корпуса в одном из направлений и нестабильности фазового угла при балансировке. Поэтому, не параллельность опор корпуса машины и фундамента, ослабление резьбовых соединений, износ посадочных мест подшипников, повышенный осевой люфт подшипников перед балансировкой ротора необходимо устранить.
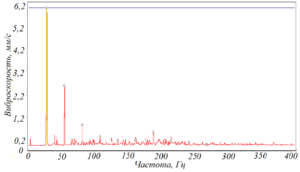
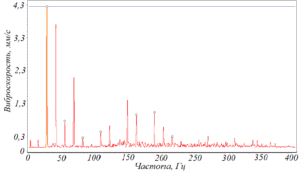
Варианты появления и развития полуторных гармоник представлены на рисунке 115. Малая амплитуда полуторной гармоники характерна для ранней стадии развития данного повреждения (рисунок 115а). Дальнейшее развитие может проходить двумя путями:
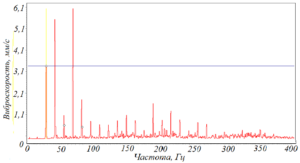
Необходимость ремонта возникает в том случае, если амплитуда полуторной гармоники превышает амплитуду оборотной частоты (рисунок 115г).
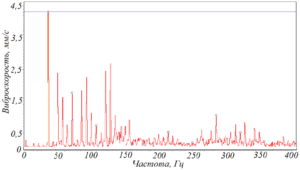
Рисунок 115 – Варианты проявления и развития полуторных гармоник:
а) ранняя стадия развития повреждения – малая амплитуда полуторной гармоники; б) развитие повреждения – увеличение амплитуды полуторной гармоники; в) развитие повреждения – появление гармоник 1¼, 1½, 1¾ и др.;
г) необходимость ремонта – амплитуда полуторной гармоники превышает
амплитуду оборотной частоты
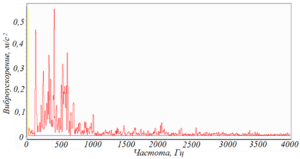
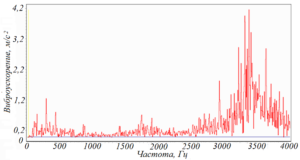
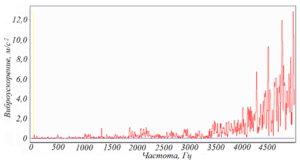
Для подшипников качения также можно выделить характерные спектрограммы виброускорения, связанные с различной степенью повреждения (рисунок 116). Исправное состояние характеризуется наличием незначительных по амплитуде составляющих в низкочастотной области исследуемого спектра 10…4000 Гц (рисунок 116а). Начальная стадия повреждений имеет несколько составляющих с амплитудой 3,0…6,0 м/с 2 в средней части спектра (рисунок 116б). Средний уровень повреждений связан с образованием «энергетического горба» в диапазоне 2…4 кГц с пиковыми значениями 5,0…7,0 м/с 2 (рисунок 116в). Значительные повреждения приводят к увеличению амплитудных значений составляющих «энергетического горба» свыше 10 м/с 2 (рисунок 116г). Замену подшипника следует проводить после начала снижения значений пиковых составляющих. При этом меняется характер трения – в подшипнике качения появляется трение скольжения, тела качения начинают проскальзывать относительно беговой дорожки.
Рисунок 116 – Этапы развития повреждений подшипника качения:
а) хорошее состояние; б) начальная стадия; в) средний уровень повреждений;
г) значительные повреждения
Анализ огибающей
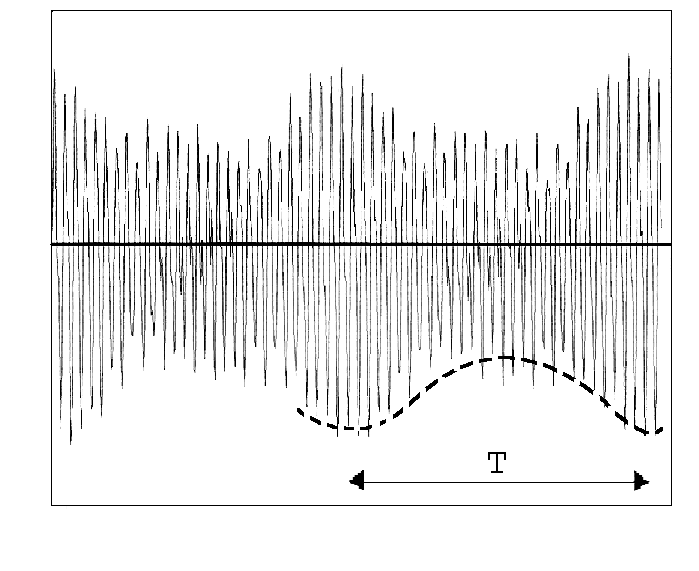
Работа подшипников качения характеризуется постоянным генерированием шума и вибрации в широкополосном частотном диапазоне. Новые подшипники генерируют слабый шум и практически незаметные механические колебания. По мере износа подшипника в вибрационных процессах начинают проявляться так называемые подшипниковые тоны, амплитуда которых растет по мере развития дефектов. В итоге вибрационный сигнал, генерируемый дефектным подшипником, можно представить, с некоторым приближением, как случайный амплитудно-модулированный процесс (рисунок 117).
Рисунок 117 – Случайный амплитудно-модулированный процесс
Форма огибающей и глубина модуляции являются весьма чувствительными показателями технического состояния подшипника качения и поэтому положены в основу анализа. В качестве меры технического состояния в некоторых программах используется коэффициент амплитудной модуляции:
В начале развития дефектов на «шумовом фоне» начинают появляться под-шипниковые тоны, которые возрастают по мере развития дефектов приблизительно на 20 дБ относительно уровня «шумового фона». На более поздних стадиях развития дефекта, когда он принимает серьезный характер, уровень шумов начинает возрастать и достигает при недопустимом техническом состоянии величины подшипниковых тонов.
Высокочастотная, шумовая часть сигнала меняет свою амплитуду во времени модулируется низкочастотным сигналом. В этом модулирующем сигнале содержится и информация о состоянии подшипника. Наилучшие результаты этот метод даёт в том случае, если анализировать модуляцию не широкополосного сигнала, а предварительно осуществить полосовую фильтрацию вибросигнала в диапазоне примерно 6…18 кГц и анализировать модуляцию этого сигнала. Для этого отфильтрованный сигнал детектируется выделяется модулирующий сигнал, который подаётся на узкополосный спектроанализатор где формируется спектр огибающей.
Небольшие дефекты подшипника не в состоянии вызвать заметные вибрации в области низких и средних частот, генерируемых подшипником. В тоже время для модуляции высокочастотных вибрационных шумов энергии возникающих ударов оказывается вполне достаточно метод обладает очень высокой чувствительностью.
Спектр огибающей имеет всегда очень характерный вид. При отсутствии дефектов он представляет собой почти горизонтальную, слегка волнистую линию. При появлении дефектов, над уровнем этой достаточно гладкой линии сплошного фона начинают возвышаться дискретные составляющие, частоты которых просчитываются по кинематике и оборотам подшипника. Частотный состав спектра огибающей позволяет идентифицировать наличие дефектов, а превышение соответствующих составляющих над фоном однозначно характеризует глубину каждого дефекта.
При диагностике подшипника качения по огибающей удается идентифицировать отдельные неисправности. Частоты спектра огибающей вибрации, на которых обнаруживаются неисправности, совпадают с частотами спектров вибрации. При измерении с использованием огибающей необходимо вводить в прибор величину несущей частоты и проводить фильтрацию сигнала (ширина пропускания не более 1/3 октавы).
Виброиспытательная система
Для того, чтобы правильно подобрать состав виброиспытательной системы, соответствующей поставленным задачам, необходимо иметь общее представление о виброиспытаниях, предельных эксплуатационных параметрах системы и знать соотношение между основными вибропараметрами.
Итак, по каким параметрам следует подбирать нужный вибростенд?
Взаимосвязь силы и виброускорения
Для начала давайте разберемся как взаимосвязана толкающая сила при синусоидальной или случайной вибрации с виброускорением.
Максимальное ускорение зависит от толкающей силы и массы испытуемого изделия. Тут всё рассчитывается просто по второму закону Ньютона.
Заявленное в паспорте вибростенда значение максимального ускорения достигается только на пустом столе, когда вибростенд толкает только массу стола. При нагружении вибростенда максимальное ускорение следует рассчитать по следующей формуле:
где m0 – масса подвижной части вибростенда, m – масса оснастки, M – масса испытуемого изделия. Суммарная масса оснастки и изделия не должна превышать заявленной в характеристиках вибростенда, иначе можно очень быстро сломать подвеску вибростенда и не получить гарантийного обслуживания.
При нагружении в горизонтальном направлении сила противодействия будет раскачивать вибростенд. Поэтому необходимо позаботиться о надёжном креплении вибростенда или приобрести у изготовителя стол скольжения, если такой предусмотрен для выбранной модели.
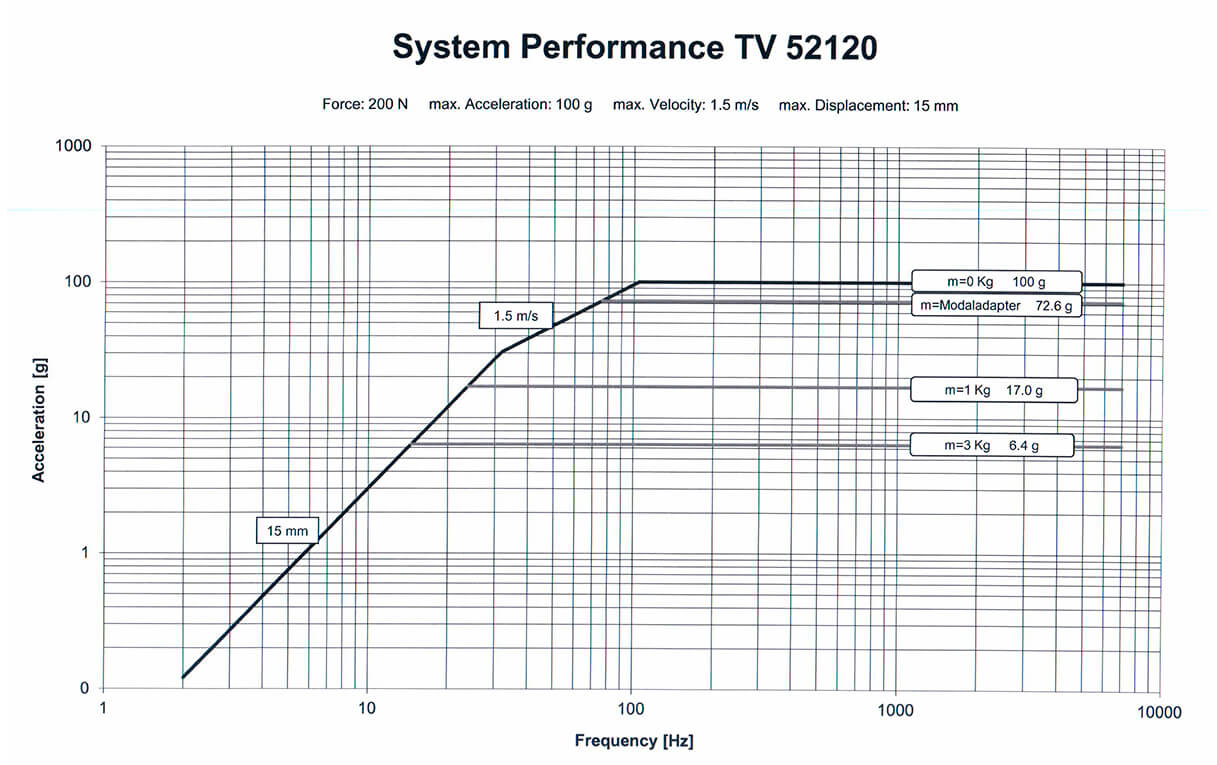
Для понимания предельных характеристик вибростенда в комплекте к эксплуатационной документации имеется график производительности вибростенда. В качестве примера приведем производительность системы TV 52120:
Взаимосвязь частоты, ускорения и виброперемещения
Нередко неопытные пользователи обращаются к нам со следующими вопросами:
В характеристиках вибростенда для синусоидальной вибрации даются: частота, амплитуда и ускорение, но ведь ускорение однозначно определяется первыми двумя величинами… Подскажите, какие параметры являются первичными в системе управления вибростендом при синусоидальной вибрации? Так скажем, если выставляем ускорение и частоту, то амплитуда уже подпирается под них автоматически? Правильно я понимаю, что при нагрузках вибростенда TV 51120 до 3 кг ускорение до 89 g будет обеспечено во всем диапазоне частот заявленных частот 2…7000 Гц?
Как уже было отмечено первичной характеристикой является толкающая сила. Она определяет максимальное ускорение вибростенда. Для безусловного проведения всех испытаний необходимо определить максимальное ускорение по профилю и максимальный вес испытуемых изделий. Если такой вибростенд оказывается неприемлемым, то толкающую силу придётся считать для каждого профиля испытаний и искать компромисс. Амплитуда перемещения определяется конструкцией вибростенда (за отдельную плату изготовитель может увеличить ход вибростенда). Частотный диапазон тоже определяется конструкцией вибростенда и чем вибростенд больше, тем меньше его верхний передел по частоте. Нижний предел по частоте определяется усилителем.
89 g вы не сможете получить на частоте 2 Гц, уж очень большое должно быть в этом случае перемещение (более 5 метров), а вот на частоте 42 Гц перемещение будет всего 12,5 мм.
Соотношение ударного и синусоидального ускорения
А что делать в случае, если требуется подобрать ситему для провевение испытаний на воздействие ударных нагрузок, а в характеристиках выбранного вибростенда не заявлено максимальное ударное ускорение?
Соотношение максимального ускорения для синусоидального сигнала и для ударного импульса определяется конструкцией вибростенда и может лежать в диапазоне от 20% до 300%. Если производитель вибростенда не указал явно ускорение или толкающую силу для ударных испытаний, то можно брать соответствующие величины для синусоидальных испытаний.
Эффективная движущая масса — это масса подвижной арматуры вибростенда, которую необходимо учитывать при нагружении вибростенда испытуемым образцом. Соответственно закон Ньютона выполняется, необходимо только правильно определить движущуюся массу.
Спектральная плотность как параметр виброиспытаний
Помимо испытаний на синусоидальную вибрацию, наиболее востребованным видом являются испытания на воздействие широкополосной случайной вибрации (ШСВ). Давайте разберемся какие имеются особенности при формировании профиля испытаний для данного вида и ответим на следующий вопрос:
Как выбрать подходящий вибростенд по необходимой спектральной плотности ШСВ?
По спектральной плотности можно определить требуемое ускорение и диапазон частот. Обычно диапазон частот не выходит за интервал 10 Гц – 2000 Гц и с ним справится любой вибростенд. Общее ускорение для испытаний на ШСВ указывается как СКЗ. Если производитель вибростенда не указал отдельно предельное ускорение для ШСВ, то нужно взять половину от указанного предельного значения ускорения.
Чтобы вычислить общее ускорение по графику спектральной плотности мощности необходимо подсчитать площадь фигуры под графиком и извлечь квадратный корень.
Ричард бейкер введение в вибрацию содержание
ОКТАВЫ И СКОРОСТЬ ИЗМЕНЕНИЯ ЧАСТОТЫ
Октавы используются для определения разницы между двумя частотами. Например, разница между частотами 10 Гц и 500 Гц составляет 490 Гц. Октавы представляют эту разницу в логарифмическом масштабе.
Почти все из нас слышали, что понятие октавы используется в музыке. У пианино разница частот между двумя ближайшими нотами одного наименования как раз составляет октаву. Международной стандартной нотой для настройки музыкальных инструментов является нота ля, частота которой равна 440 Гц. Частота ноты октавой выше равна 880 Гц, а октавой ниже – 220 Гц. Таким образом, мы видим, что октава обладает свойством удваивания, другими словами это логарифмическое отношение.
Что бы определить количество октав между двумя частотами можно использовать следующую формулу:
где f н – нижняя частота, f в – верхняя частота.
При испытаниях скользящей синусоидой используется логарифмический масштаб изменения частоты. Это делается с целью обеспечения условий равного нагружения объекта испытаний на разных частотах. Так при частоте 10 Гц за 1секунду происходит 10 циклов колебаний. Эти же 10 циклов колебаний занимают одну сотую секунды при частоте 1000 Гц. Это значит, что для обеспечения равнонагруженного состояния (равного количества циклов колебаний) на разных частотах с увеличением частоты время колебаний на этой частоте должно уменьшаться.
ЧТО ТАКОЕ СЛУЧАЙНАЯ ВИБРАЦИЯ?
Если мы возьмем конструкцию, состоящую из нескольких балок различной длины и начнем ее возбуждать скользящей синусоидой, то каждая балки будет интенсивно колебаться при возбуждении ее собственной частоты. Однако если мы возбудим эту же конструкцию широкополосным случайным сигналом, то мы увидим, что все балки начнут сильно раскачиваться, как будто в сигнале одновременно присутствуют все частоты. Это так и в то же время не так. Картина будет более реальной, если мы предположим, что в течение некоторого промежутка времени эти частотные компоненты присутствуют в сигнале возбуждения, но их уровень и фаза изменяются случайным образом. Время – вот ключевой момент в понимании случайного процесса. Теоретически мы должны учитывать бесконечный период времени, чтобы иметь истинный случайный сигнал. Если сигнал действительно случайный, то он никогда не повторяется.
Раньше для анализа случайного процесса применялась аппаратура на основе полосовых фильтров, которые выделяли и оценивали отдельные частотные составляющие. Современные анализаторы спектров используют алгоритм быстрого преобразования Фурье (БПФ). Случайный непрерывный сигнал измеряется и дискретизируется по времени. Затем для каждой временной точки сигнала вычисляется синусная и косинусная функции, которые определяют уровни частотных компонент сигнала, присутствующих в анализируемом периоде сигнала. Далее проводится измерение и анализ сигнала для следующего временного интервала и его результаты усредняются с результатами предыдущего анализа. Так повторяется до тех пор, пока не будет получено приемлемое усреднение. На практике число усреднений может колебаться от двух – трех до нескольких десятков и даже сотен.
На рисунке, представленном ниже, показано как сумма синусоид с различными частотами образуют сигнал сложной формы. Может показаться, что суммарный сигнал является случайным. Но это не так, потому что составляющие имеют постоянную амплитуду и и фазу и изменяются по синусоидальному закону. Таким образом, показанный процесс периодический, повторяющийся и предсказуемый.
В действительности случайный сигнал имеет составляющие, амплитуды и фазы которых изменяются случайным образом.
На рисунке ниже показан спектр суммарного сигнала. Каждая частотная составляющая суммарного сигнала имеет постоянную величину, но для истинно случайного сигнала величина каждой составляющей будет все время изменяться и спектральный анализ покажет усредненные по времени значения.
Единица gn 2 /Гц используется при вычислении спектральной плотности и по существу выражает среднюю мощность, заключенную в частотном диапазоне шириной 1 Гц. Из профиля испытаний случайной вибрацией мы можем определить суммарную мощность, сложив мощности каждого диапазона шириной 1 Гц. Профиль, показанный ниже, имеет всего три диапазона шириной 1 Гц, но рассматриваемый метод применим к любому профилю.
( 4 g 2 /Гц = 4g скв 2 в каждом диапазоне шириной 1 Гц)
Суммарное ускорение (перегрузку) gn скв профиля можно получить сложением, но так как значения являются среднеквадратическими, то они суммируются следующим образом:
Такой же результат можно получить используя более общую формулу:
Однако профили случайной вибрации, используемые в настоящее время, редко являются плоскими и больше похожи на горный массив в разрезе.
Частота, Гц (лог. шкала)
На первый взгляд определение суммарного ускорения gn показанного профиля задача довольно простая, и определяется как среднеквадратическая сумма значений четырех сегментов. Однако профиль показан в логарифмическом масштабе и наклонные прямые на самом деле не прямые. Эти линии являются экспоненциальными кривыми. Поэтому нам нужно вычислить площадь под кривыми, а это задача намного сложнее. Как это сделать, мы рассматривать не будем, но можно сказать, что суммарное ускорение равно 12.62 g скв.
Для чего нужно знать суммарное ускорение при случайной вибрации?
В режиме случайной вибрации вибрационная испытательная система имеет номинальную толкающую силу, которая выражается в Н скв или кгс скв. Заметьте, что сила определяется среднеквадратическим значением в отличие от синусоидальной вибрации, где используется амплитудное значение. Формула для определения силы такая же: F = m*a, но так как сила имеет среднеквадратическое значение, то и ускорение должно быть среднеквадратическим.
Сила (Н скв.) = масса (кг) * ускорение (м/с 2 скв.)
Сила (кгс скв.) = масса (кг) * ускорение (gn скв.)
Помните, что под массой понимается общая масса всех подвижных частей!
Что понимается под перемещением при случайной вибрации?
Для нас важно знать перемещение при заданном профиле испытаний, так как оно может превысить максимально допустимое перемещение вибратора. Не вдаваясь в подробности, мы знаем, как рассчитать суммарное среднеквадратическое ускорение и нет причин мешающих нам определить среднеквадратическую скорость и среднеквадратическое перемещение для данного профиля. Трудности появляются тогда, когда мы хотим перейти от среднеквадратического значения к амплитудному или к размаху. Давайте вспомним, что отношение амплитудного значения к среднеквадратическому называется пик-фактором, который для синусоидального сигнала равен корню квадратному из 2. Коэффициенты перехода от среднеквадратического значения к амплитудному и обратно равны соответственно 1.414 (2) и 0.707 (1/2). Однако мы имеем дело не с синусоидальным сигналом, а со случайным процессом, у которого теоретический пик-фактор равен бесконечности, так как амплитудное значение случайного сигнала может быть равно бесконечности. На практике значение пик-фактора принимают равным 3. На рисунке показана кривая нормального распределения случайного сигнала. По статистике, если ограничиться шириной интервала 3, то это охватит 99.73% всех возможных значений амплитуд истинного случайного сигнала.
Кривая нормального распределения
Следовательно, если принять, что при пик-факторе равном трем контроллер случайной вибрации будет генерировать случайный сигнал с максимальной амплитудой в три раза превышающей среднеквадратическое значение, то из этого следует, что расчетное перемещение будет равно суммарному среднеквадратическому перемещению умноженному на значение пик-фактора и умноженному на 2. Это расчетное перемещение не должно превышать максимально допустимое перемещения вибратора.
Практические аспекты выбора значения пик-фактора
Мы можем сделать так, чтобы контроллер случайной вибрации генерировал сигнал с пик-фактором равным 3, который через вибратор будет передаваться испытываемому образцу. К сожалению и вибратор и образец являются существенно нелинейными системами и имеют резонансы. Эта нелинейность с резонансами будет вызывать искажения. В конечном итоге мы увидим, что пик-фактор, измеренный на столе вибратора или объекте испытаний, будет значительно отличаться от первоначально заданного! Контроллеры случайной вибрации не корректируют это автоматически.
Внеполосовая мощность
Узкополосная случайная вибрация
Толкающая сила вибраторов в режиме случайной вибрации измеряется при следующих условиях:
масса нагрузки примерно в два раза больше массы арматуры (подвижной части вибратора)
профиль испытаний соответствует стандарту ISO 5344
20 Гц – 100 Гц Наклон = +20 дБ/декада (» +6 дБ/октава)
100 Гц – 2000 Гц Наклон = 0 дБ/декада (плоский)
отношение амплитудного значения к среднеквадратическому значению ускорения не менее 3-х.
Вибрационные испытательные системы имеют нелинейную частотную характеристику (на одних частотах их эффективность выше, на других ниже), и случайный процесс на частотах ниже 500 Гц воспроизводится с меньшей эффективностью. В этом случае усилителю может не хватить мощности, чтобы создать необходимую толкающую силу. Выбор более мощного усилителя решит эту проблему.
ЕДИНИЦЫ ИЗМЕРЕНИЯ СПЕКТРАЛЬНОЙ ПЛОТНОСТИ
Наиболее часто используемые единицы измерения плотности спектра мощности следующие: