что такое социальный граф

Анализ социального графа

Анализ социальных сетей (Social Network Analysis) существовал задолго до Интернета, но в последнее время набирает обороты.

Мне было интересно посмотреть, как эффективно алгоритм, выделяющий кластеры в графах, сработает для некоторых групп в Twitter, которые представляют для меня интерес.

23 января в Запорожье пройдет #UKRTWEET — первый всеукраинский баркэмп посвященный Twitter. Граф выше показывает, кто из его участников, с кем разговаривает и кого упоминает.

Заметка ниже посвящена анализу этого графа. Весь код используемых здесь скриптов лежит на github. Изложение, в какой-то мере, вдохновлено недавно упомянутой на Хабре книгой Тоби Сегаран «Программируем коллективный разум», код примеров которой доступен на сайте автора.

Также о data mining в Twitter я говорил 16 января на первой в этом году донецкой встрече «Кофе и код». Поэтому здесь параллельно проведу анализ группы людей из Донецка, которые пишут в Twitter. Кстати, в этом году донецкие встречи будут регулярными — каждую третью субботу месяца (следующая 20 февраля). Следите за группой.

1. Получение информации

Для начала, получаем список всех участников групп. Список участников #UKRTWEET есть на странице баркэмпа. Скачиваем и парсим его при помощи BeautifulSoup (код). Для людей, которые твитят из Донецка, я веду список @dudarev/donetsk. Сохраняем его участников при помощи библиотеки tweepy (код).

Для каждого из участников скачиваем последние 100 твитов и сохраняем их. Tweepy автоматически парсит JSON, а так как в этот раз мы хотим сохранить данные такими какие они есть, то немного подправляем класс tweepy.API (код).

2. О чем говорят

Теперь можно анализировать информацию. И сначала — пара наблюдений не связанных с социальным графом. Давайте посмотрим какие хэштеги наиболее часто употреблялись каждой группой. Для этого напишем утилиту, которая принимая строку возвращает список всех встречающихся в ней хэштегов. Для ее написания TDD — весьма кстати (смотрим код). С помощью этой утилиты парсим все твиты (код).

3. Когда говорят

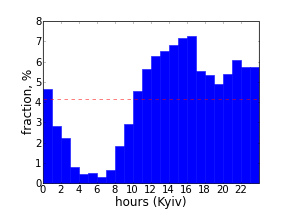
Давайте посмотрим, в какое время, группа проявляет наибольшую активность. Для этого воспользуемся тем же самым скриптом, пробегающим по всем твитам, но на этот раз сформируем списки количества твитов в данный час дня и сохраним их в отдельных файлах (опция ‘-t’ при вызове из коммандной строки). Изобразим диаграмы при помощи библиотеки Matplotlib (код).

Участники #UKRTWEET проявляют активность выше средней с 10 утра до 1 часа ночи по киевскому времени, с пиком около 5 часов вечера.

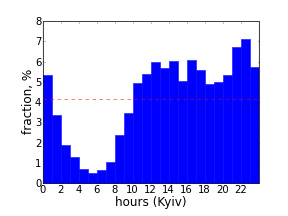
Дончане активны в то же время, но пик наблюдается около 11 вечера. Быть может, это потому что люди собирающиеся на баркэмп рассматривают Twitter как рабочий инструмент и активны в нем в рабочее время. Хотя, из-за недавних праздников, эти данные могут быть не показательными.

4. Социальный граф

Граф из данных Twitter можно строить различными способами. Здесь мы будем следовать следующей конструкции: если человек А упомянул человека Б хотя бы один раз (не важно ретвит или ответ), от вершины А к вершине Б строим ориентированное ребро. Граф не взвешенный, то есть ребро строим только единожды.

Все тот же скрипт с опцией ‘-g’ выстраивает из сохраненных твитов словарь представляющий такой граф и сохраняет его в формате JSON для последующего анализа (код).

Несколько количественных наблюдений. В группе #UKRTWEET 58% упоминают кого-то из группы (61/106). А всего упоминают 1221 человека что в 11.5 раз больше самой группы (1221/106).

В донецкой же группе 51.6% вовлечены в группу (116/225), а всего различных упоминаний в 6 раза больше самой группы (1341/225). Явно, что люди, которые собираются посетить баркэмп о Twitter более активно используют его как средство общения.

5. Авторитетность

Авторитетность в социальном графе можно анализировать разными способами. Самый простой — отсортировать участников по количеству входящих ребер. У кого больше — тот больше авторитетен. Такой способ годен для небольших графов. В поиске по Интернету Google в качестве одного из критериев для авторитетности страниц использует PageRank. Он вычисляется при помощи случайного блуждания по графу, где в качестве узлов — страницы, а ребро между узлами — если одна страница ссылается на другую. Случайный блуждатель двигается по графу и время от времени перемещается на случайный узел и начинает блуждание заново. PageRank равен доли пребывания на каком-то узле за все время блуждания. Чем он больше, тем узел более авторитетен.

Здесь мы остановимся только на двух вышеупомянутых критериях. Стоит упомянуть, что при анализе социальных графов еще большое внимание уделяют различным центральностям. Их использование в качестве критерия авторитетности может иметь больший смысл для более распределенных социальных графов.

Одна из распространенных библиотек Python для работы с графами — NetworkX. Ее и будем использовать. Создав граф G, считать различные его параметры очень удобно. Так, например, чтобы посчитать PageRank всех узлов, достаточно написать:

Хочется подчеркнуть, что все числа ниже — для искуственно выделенных из твиттерсферы групп. Другие участники этих групп, могут быть глобально более влиятельными и авторитетными. Числа ниже — для комуникаций внутри данных групп.

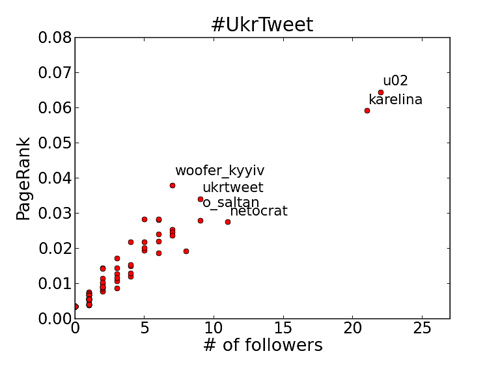
Давайте отобразим зависимость PageRank для всех узлов от количества узлов, которые на них указывают (код).

Естественно, большой авторитет у двух организаторов (@karelina и @u02). У известного украинского блогера @woofer_kyyiv авторитетность измеряемая в PageRank высока, хотя и упоминают меньше людей, но упоминают равномерно по группе (из разных сообществ). Авторитетность официального аккаунта баркэмпа (@ukrtweet) ниже при большем упоминании. Одна из интерпретаций: люди предпочитают общаться и упоминать людей. Быть может поэтому во многих официальных западных аккаунтах явно указываются имена вещающих.

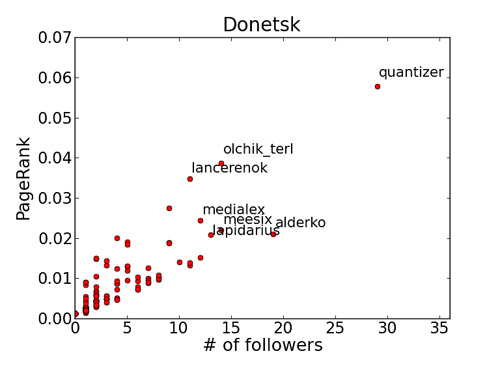
Безусловный лидер внутри донецкой группы — @quantizer. Различия в PageRank при схожих количествах упоминаний для следующих участников можно трактовать, например, так: @olchik_terl и @lancerenok больше общаются с людьми из разных частей социального графа группы, тогда как @medialex, @lapidarius, @meesix, @alderko больше взаимодействуют со своими локальными сообществами (в основном выделенными по профессиональному признаку, об этом ниже), поэтому у второй группы PageRank чуть ниже, чем у первой.

6. Влияющие извне

Как усовершенствование, можно складывать не единицы, а PageRank упоминающих. Так те, которые извне больше влияют на влиятельных в группе, будут иметь больший вес. Оставляем это для желающих в качестве упражнения с кодом.

7. Сообщества

Для алгоритмического поиска кластеров в графах наиболее популярны методы оптимизирующие модулярность. Модулярность — количественный параметр использующий количество внутренних связей внутри предполагаемых сообществ и связей с внешними сообществами. Все результаты, что будут обсуждены ниже, получены при помощи кода выложеному на сайте бельгийской группы, который они описали в статье выложенной на arxiv. Другие люди тоже выкладывали свой код для подобных целей. Также алгоритм кластеризации встроен в другую популярную библиотеку для работы с графами — igraph.

Графы с метками и сообществами отображенные с помощью Seadragon, интересного веб-приложения от Microsoft позволяющем легко выкладывать большие графические файлы в интерфейсе подобному онлайн-картам, а также одним файлом:

Использовались скрипт для нахождения сообществ и скрипт для рисования графа.

8. Метки для сообществ

Хотелось бы получить какую-нибудь характеристику сформировавшихся сообществ. Один из способов — посмотреть в какие списки включались люди из сообществ. Скачиваем все списки, в которые были включены люди из групп (код). Сортируем группы по суммарному PageRank и печатаем десять названий списков, которые встречались для наибольшего количества людей в группе (код). В некоторых сообществах нельзя выделить говорящие метки, но во многих метки участников о многом говорят. В таблице ниже сообщества отсортированы по суммарном PageRank, двое самых авторитетных участника, количество участников, несколько говорящих общих меток (в скобках количество человек из сообществ которые были в соответствующих списках):

UkrTweet

Еще о четырех сообществах трудно что-то сказать на основе списков. Я, например, попал в сообщество, из которого многи ретвитили о tweetingplaces, одном моем проекте. Но общих названий списков у нас, кроме ukrtweet, нет.

Донецк

Что интересно, olchik_terl и lancerenok, которые упоминались ранее, и у кого PageRank был больше, чем у других людей, которые так же часто упоминаются, попадают в активные сообщества, которые плохо описываются списками. Они же больше общаются со всей группой, а не внутри профессиональных сообществ.

Упражнения

Используемые библиотеки

BeautifulSoup
для парсинга HTML
tweepy
интерфейс для доступа к Twitter API
NetworkX.
для работы с графами
Matplotlib
позволяет рисовать графики и диаграммы
igraph
пакет для работы с графами, есть интерфейс на Python (здесь не использовался, но упоминался)

Источник

Теория графов и социальные сети

Тема: Наука

Теория графов — раздел дискретной математики, изучающий свойства графов. В общем смысле граф представляется как множество вершин (узлов), соединённых рёбрами.

Теория графов находит применение, например, в геоинформационных системах. Существующие или вновь проектируемые дома, сооружения, кварталы и т. п. рассматриваются как вершины, а соединяющие их дороги, инженерные сети, линии электропередачи и т. п. — как рёбра.

Применение различных вычислений, производимых на таком графе, позволяет, например, найти кратчайший объездной путь или ближайший продуктовый магазин, спланировать оптимальный маршрут.

Теория графов содержит большое количество нерешённых проблем и пока не доказанных гипотез.

История возникновения теории графов

Родоначальником теории графов считается выдающийся математик, член Петербургской академии наук Леонард Эйлер.

В 1736 году в одном из своих писем он формулирует и предлагает решение задачи о семи кёнигсбергских мостах, ставшей впоследствии одной из классических задач теории графов.

Издавна среди жителей Кёнигсберга была распространена такая загадка: как пройти по всем мостам (через реку Преголя), не проходя ни по одному из них дважды. Многие кёнигсбержцы пытались решить эту задачу как теоретически, так и практически, во время прогулок. Впрочем, доказать или опровергнуть возможность существования такого маршрута никто не мог.

В 1736 году задача о семи мостах заинтересовала Леонарда Эйлера, о чём он написал в письме итальянскому математику и инженеру Мариони от 13 марта 1736 года. В этом письме Эйлер пишет о том, что он смог найти правило, пользуясь которым, легко определить, можно ли пройти по всем мостам, не проходя дважды ни по одному из них. Ответ был «нельзя».

На упрощённой схеме части города (графе) мостам соответствуют линии (дуги графа), а частям города — точки соединения линий (вершины графа). В ходе рассуждений Эйлер пришёл к следующим выводам:

Граф кёнигсбергских мостов имел четыре (синим) нечётные вершины (то есть все), следовательно, невозможно пройти по всем мостам, не проходя ни по одному из них дважды.

Изображение графов на плоскости

При изображении графов на рисунках чаще всего используется следующая система обозначений: вершины графа изображаются точками или, при конкретизации смысла вершины, прямоугольниками, овалами и др. где внутри фигуры раскрывается смысл вершины (графы блок-схем алгоритмов).

Если между вершинами существует ребро, то соответствующие точки (фигуры) соединяются отрезком или дугой. В случае ориентированного графа дуги заменяют стрелками, или явно указывают направленность ребра.

Не следует путать изображение графа с собственно графом (абстрактной структурой), поскольку одному графу можно сопоставить не одно графическое представление.

Изображение призвано лишь показать, какие пары вершин соединены рёбрами, а какие — нет. Часто на практике бывает трудно ответить на вопрос, являются ли два изображения моделями одного и того же графа или нет (другими словами, изоморфны ли соответствующие изображениям графы). В зависимости от задачи, одни изображения могут давать более наглядную картину, чем другие.

Социальный граф

Социальный граф (англ. Social graph) — это граф, узлы которого представлены социальными объектами, такими как пользовательские профили с различными атрибутами (например: имя, день рождения, родной город и т. д.), сообщества, медиа-контент и т. д., а ребра — социальными связями между ними.

Неявный социальный граф (англ. Implicit social graph) — это такой граф, который можно сформировать на основе взаимодействий пользователя со своими «друзьями» и группами «друзей» в социальной сети. В этом графе в отличие от обычного социального графа нет явного указания «друзей», то есть нет явных социальных связей.

С помощью социальных графов решают такие задачи, как: идентификация пользователей; социальный поиск; генерация рекомендаций по выбору «друзей», медиа-контента, новостей; выявление «реальных» связей или сбор открытой информации для моделирования графа.

Обработка данных социальных графов связана с рядом проблем, как например различия социальных сетей, закрытость социальных данных.

Задачи

Идентификация пользователей

Обнаружение профилей, принадлежащих одному человеку, в нескольких социальных сетях. Решение этой задачи позволяет получить более полный социальный граф, что может быть полезно во многих задачах, таких как:

Социальный поиск
Поиск социальных объектов (пользователей, их данных, их записей и т. д.), основанный на анализе набора связей, в которых находятся искомые объекты.

Генерация рекомендаций
Важной задачей является поиск точных алгоритмов генерации рекомендаций и предложений пользователям, который так же используется при создании графа интересов на основе социального графа.

Существуют традиционные подходы в области рекомендательных систем:

Выявление «настоящих» связей

Применение подхода «разведки на основе открытых источников» для выявления истинных связей между пользователями, то есть настоящих друзей, родственников и т. п.

Граф интересов

Граф интересов — это онлайн представление интересов конкретного человека, полученное на основе его активности в социальных сетях.

Вершинами графа являются увлечения личности, также вершиной может быть профиль человека в социальной сети, ребра графа отображают взаимоотношения между вершинами графа.

С помощью графа интересов можно понять, что человек хочет сделать, купить, куда хочет пойти, с кем может встретиться, за чьими сообщениями ему интересно следить или за кого он готов проголосовать.

Cвязи в графе интересов

В графе интересов могут существовать различные типы связей, которые позволяют пользователю выходить за рамки обычных социальных сетей. Например, человеку нужно найти ответ на интересующую его тему, который не может дать ни один из старых друзей и знакомых. В этом случае выстраивается цепочка из трех типов связей:

Граф интересов также может быть представлен в виде взвешенного графа, в этом случае вес ребра означает силу взаимосвязи между вершинами.

При построении такого графа изначально вводится предположение о том, что взаимосвязи имеют одинаковую силу, например, интерес к машинам и к театру неизвестен, и взаимосвязь двух интересов устанавливается в виде бесконечно большого числа. Затем, если будет обнаружено, что люди, интересующиеся машинами, ведут себя похожим образом с теми людьми, которые увлекаются театром, то значение веса ребра между вершинами, обозначающими данные увлечения, будет уменьшено.

Отношения между графом интересов и социальным графом

Граф интересов и социальный граф тесно взаимосвязаны, но это не одно и то же.

Граф интересов используется для создания сети интересов людей. В то время как Facebook и другие социальные сети организованы вокруг друзей человека, то есть вокруг социального графа, сети увлечений созданы вокруг интересов личностей, их графа интересов.

Подобно тому как социальный граф — это карта взаимосвязей личности с теми, кто «следует» за ней в сети, граф интересов — это так же взаимосвязь с интересами личности в сети.

Таким образом, увлечения человека, представленные в виде графа интересов, обеспечивают средства для дальнейшей персонализации веб-пространства, основанной на пересечении графа интересов с веб-контентом. Граф интересов или сеть интересов в некоторых случаях могут быть получены из социального графа или социальной сети и могут поддерживать и обновлять связи между вершинами на основе данной социальной сети.

Граф интересов должен быть точным и выразительным, он должен принимать во внимание явно объявленные интересы, например, «Like» на Facebook или «интересы» в профиле на LinkedIn, а также неявные интересы, выведенные на основе активности пользователя, например, такие как щелчки мышью, комментарии, теги к фото и чек-ины. Социальные сети часто являются источником этой информации.

Использование графа интересов

Существует несколько способов использования графа интересов, как с точки зрения потребителя, так и с точки зрения бизнесмена. В сочетании с социальным графом, граф интересов может быть применён для установления связей между пользователями в социальных сетях или в реальном мире. В таких сетях пользователи могут указывать и делиться своими увлечениями, но при этом им не обязательно знать друг друга.

Граф интересов так же может быть применён в маркетинге, в целях анализа аудитории проекта и дальнейших продаж на основе этой информации, для анализа тональности текста и для таргетированной рекламы, основанной на интересах.

Например, такие компании как Twitter с помощью графа интересов имеют возможность делать рекламу более направленной на конкретного пользователя, основываясь на его увлечениях.

Также граф интересов может использоваться при создании продукции с учётом пожеланий потребителя, он помогает определить какие особенности и возможности следует предоставить в следующих версиях. Граф интересов имеет множество других применений включая задачи обнаружения содержимого и фильтрации для предоставления рекомендаций по фильмам, книгам, музыке и так далее.

Если вы хотите получать больше статей, подобно этой, то кликните Recommend ниже.

Источник

Социальный граф

Содержание

Метрики

Говоря о задачах на социальном графе, употребляют термин метрики, которые в числовой форме отображают характеристики социальных объектов, сегментов/групп объектов и их связей.

Взаимоотношения

Данные метрики отображают характер взаимоотношений одного социального объекта с другими социальными объектами.

Связи

Данные метрики отображают особенности связей, как для отдельных социальных объектов, так и для графа в целом.

Сегментация

Данные метрики отображают характеристики социального графа, поделенного на сегменты, которые имеют отличительные особенности.

Модели

В данном разделе приведены общеизвестные модели графов, которые потенциально могут заменить «реальные» социальный графы. [19]

Функционально-управляемые модели (англ. Feature-driven Models ) нацелены на воспроизведение статистических характеристик графа, таких как степенное распределение и динамические изменения плотности графа.

Намеренно-управляемые модели (англ. Intent-driven Models ) сфокусированы на эмуляцию процесса создания оригинального графа.

Структурно-управляемые модели (англ. Structure-driven Models ) охватывают статистические данные из структуры графа, позволяя соответствующему генератору воспроизводить случайные графы с теми же структурными ограничениями.

Задачи

Идентификация пользователей

Обнаружение профилей, принадлежащих одному человеку, в нескольких социальных сетях. [20] Решение этой задачи позволяет получить более полный социальный граф, что может быть полезно во многих задачах, таких как:

Социальный поиск

Поиск социальных объектов (пользователей, их данных, их записей и т. д.), основанный на анализе набора связей, в которых находятся искомые объекты. [3]

Генерация рекомендаций

Важной задачей является поиск точных алгоритмов генерации рекомендаций и предложений пользователям.

Подходы к рекомендациям

Существуют традиционные подходы в области рекомендательных систем [22] :

Выявление «настоящих» связей

Применение подхода «разведки на основе открытых источников» (англ. Open source intelligence, OSINT ) для выявления истинных связей между пользователями, то есть настоящих друзей, родственников и т. п. [24]

Сбор информации

Построение социального графа на основе данных, полученных в результате парсинга веб-сервисов провайдеров социальных сетей.

Для оценивания задачи ставятся следующие критерии: [25]

При обходе оценивают следующие факторы:

Проблемы

Различия социальных сетей

Для задачи индетификации пользователей главной проблемой являются различия социальных сетей. В основном играют роль семантика связей между социальными объектами и социальные графы различных топологий. [20]

Генерация рекомендаций

Основной проблемой генерации рекомендаций является проблема холодного старта — расчёт рекомендации для новых социальных объектов (пользователей, постов, медиа-контента и т. д.). [22]

Закрытость социальных данных

Главная проблема сбора данных для социального графа заключается в закрытости социальных сетей. [26]

Во-первых, трудно получить социальный граф от «провайдеров» [27] из-за цености и защищености законом социальных данных.

Во-вторых, большой проблемой является сбор миллионов списков контактов, профилей, фотографий, видео и т. п. парсерами. Многие «провайдеры» социальных сетей используют Single Page Application или множество динамических страниц, содержащих Ajax и DHTML, что создает очень много проблем для создания гибкого парсера.

См. также

Примечания

Литература

Полезное

Смотреть что такое «Социальный граф» в других словарях:

Социальная сеть (социология) — У этого термина существуют и другие значения, см. Социальная сеть. Социальная сеть (англ. social network) социальная структура (математически социальный граф), состоящая из группы узлов, которыми являются социальные объекты (люди или… … Википедия

Коллаборативная фильтрация — Эта статья в данный момент активно редактируется участником Участник:Moshanin. Пожалуйста, не вносите в неё никаких изменений до тех пор, пока не исчезнет это объявление. В противном случае могут возникнуть конфликты редактирования. Данное… … Википедия

Сен-Симон Анри Клод — (граф Saint Simon) известный социальный реформатор. Происходил из фамилии, считавшей своим родоначальником Карла Великого, род. в 1760 г. В его воспитании принимал участие д Аламбер. Тринадцати лет от роду он имел смелость сказать своему глубоко… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Сен-Симон, Анри — граф Клод Анри де Сен Симон Claude Henri de Rouvroy, comte de Saint Simon … Википедия

Пушкин, Александр Сергеевич — — родился 26 мая 1799 г. в Москве, на Немецкой улице в доме Скворцова; умер 29 января 1837 г. в Петербурге. Со стороны отца Пушкин принадлежал к старинному дворянскому роду, происходившему, по сказанию родословных, от выходца «из… … Большая биографическая энциклопедия

Немецкая литература — Литература эпохи феодализма. VIII X века. XI XII века. XII XIII века. XIII XV века. Библиография. Литература эпохи разложения феодализма. I. От Реформации до 30 летней войны (конец XV XVI вв.). II От 30 летней войны до раннего Просвещения (XVII в … Литературная энциклопедия

Либерализм — (Liberalism) Либерализм это политическое и филосовское учение, которое выступает за снижение вмешательства государства в жизнь граждан Основы либерализма, происхождение, формы либерализма, развитие либеральной мысли, современный либерализм,… … Энциклопедия инвестора

Герцен, Александр Иванович — — родился 25 го марта 1812 г. в Москве. Он был внебрачным сыном родовитого московского помещика Ивана Алексеевича Яковлева. Последний принадлежал к тому поколению, которое Г. впоследствии называл «иностранцами дома, иностранцами в… … Большая биографическая энциклопедия

Германия — Федеративная Республика Германии (ФРГ), гос во в Центр. Европе. Германия (Germania) как территория, заселенная герм, племенами, впервые упоминается Пифеем из Массалии в IV в. до н. э. Позже название Германия использовалось для обозначения рим.… … Географическая энциклопедия

Источник