что такое сообщающиеся сосуды физика 7 класс
Закон сообщающихся сосудов и его применение.
Сообщающиеся сосуды – это сосуды, соединенные между собой ниже уровня жидкости в каждом из сосудов. Таким образом жидкость может перемещаться из одного сосуда в другой.
Перед тем как понять принцип действия сообщающихся сосудов и варианты их использования необходимо определиться в понятиях, а точнее разобраться с основным уравнением гидростатики.
Содержание статьи
Закон сообщающихся сосудов
Итак, сообщающиеся сосуды имеют одно общее дно и закон о сообщающихся сосудах гласит:
Какую бы форму не имели такие сосуды, на поверхности однородных жидкостей в состоянии покоя на одном уровне действует одинаковое давление.
Для иллюстрации этого закона и возможностей его применения начнем с рассмотрения основного уравнения гидростатики.
Основное уравнение гидростатики
где P1 – это среднее давление на верхний торец призмы,
P – давление на нижний торец,
g – ускорение свободного падения,
h – глубина погружения призмы под свободной поверхностью жидкости.
ρgh – сила тяжести (вес призмы).
Звучит уравнение так:
Давление на поверхность жидкости, произведенное внешними силами, передается в жидкости одинаково во всех направлениях.
Из написанного выше уравнения следует, что если давление, например в верхней точке изменится на какую-то величину ΔР, то на такую же величину изменится давление в любой другой точке жидкости
Доказательство закона сообщающихся сосудов
Возвращаемся к разговору про сообщающиеся сосуды.
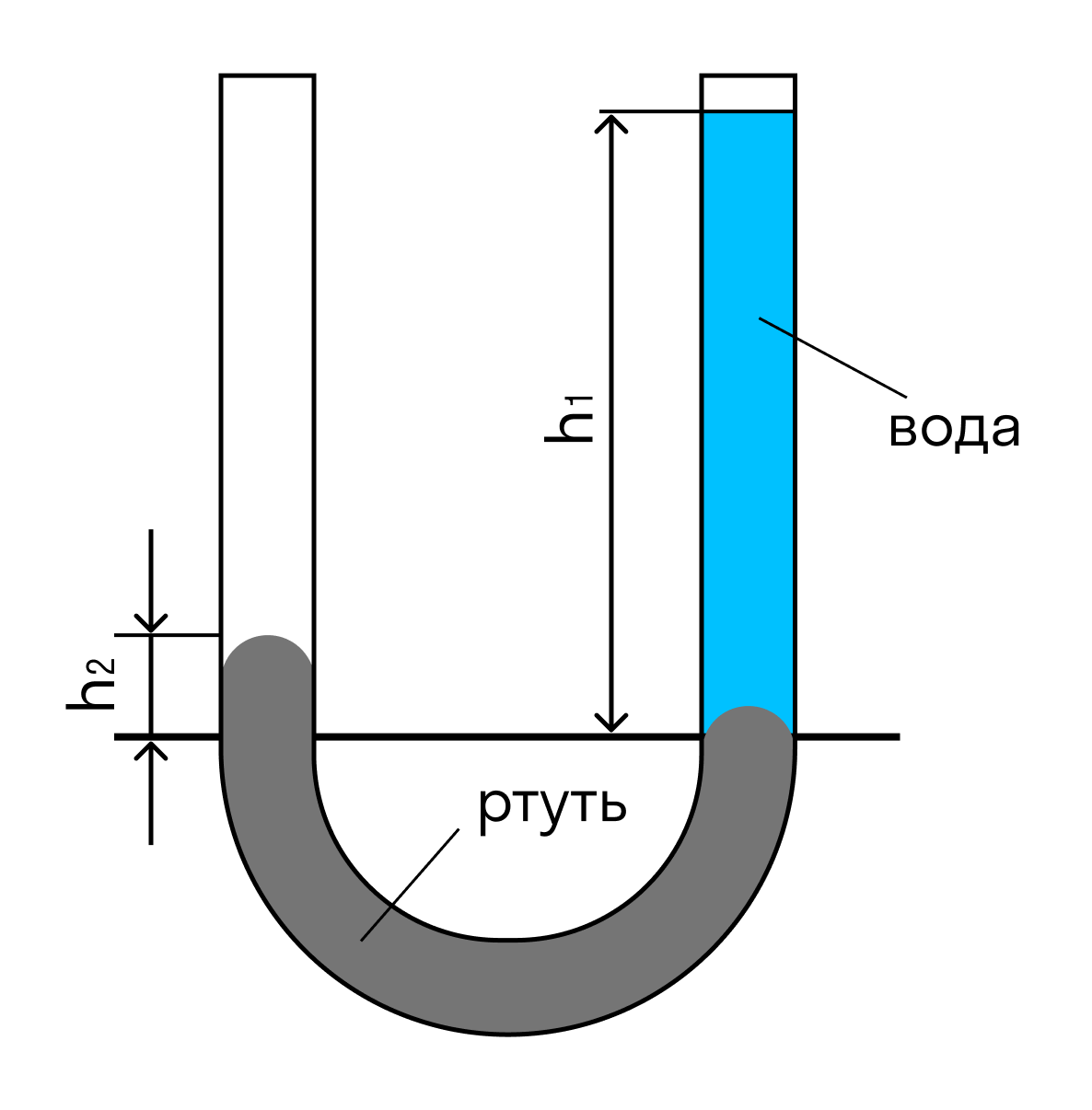
Предположим, что имеются два сообщающихся сосуда А и В, заполненные различными жидкостями с плотностями ρ1 и ρ2. Будем считать, что в общем случае сосуды закрыты и давления на свободных поверхностях жидкости в них соответственно равны P1 и P2.
Пусть поверхностью раздела жидкостей будет поверхность ab в сосуде А и слой жидкости в этом сосуде равен h1. Определим в заданных условиях уровень воды в сообщающихся сосудах – начнем с сосуда В.
Гидростатическое давление в плоскости ab, в соответствии с уравнение гидростатики
если определять его, исходя из известного давления P1 на поверхность жидкости в сосуде А.
Это давление можно определить следующим образом
где h2 – искомая глубина нагружения поверхности ab под уровнем жидкости в сосуде В. Отсюда выводим условие для определения величины h2
P1 + ρ1gh1 = P2 + ρ2gh2
т.е. закон сообщающихся сосудов состоит в следующем.
В сообщающихся сосудах при одинаковом давлении на свободных поверхностях высоты жидкостей, отсчитываемые от поверхности раздела, обратно пропорциональны плотностям жидкостей.
Свойства сообщающихся сосудов
Если уровень в сосудах одинаковый, то жидкость одинаково давит на стенки обоих сосудов. А можно ли изменить уровень жидкости в одном из сосудов.
Можно. С помощью перегородки. Перегородка, установленная между сосудами перекроет сообщение. Далее доливая жидкость в один из сосудов мы создаем так называемый подпор – давление столба жидкости.
Если затем убрать перегородку, то жидкость начнет перетекать в тот сосуд где её уровень ниже до тех пор пока высота жидкости в обоих сосудах не станет одинаковой.
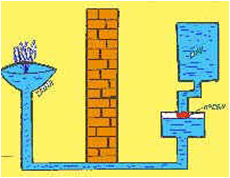
В быту этот принцип используется например в водонапорной башне. Наполняя водой высокую башню в ней создают подпор. Затем открывают вентили, расположенные на нижнем этаже и вода устремляется по трубопроводам в каждый подключенный к водоснабжению дом.
Приборы основанные на законе сообщающихся сосудов
На принципе сообщающихся сосудов основано устройство очень простого прибора для определения плотности жидкости. Этот прибор представляет собой два сообщающихся сосуда – две вертикальные стеклянные трубки А и В, соединенные между собой изогнутым коленом С. Одна из вертикальных трубок заполняется исследуемой жидкостью, а другая жидкостью известной плотности ρ1 (например водой), причем в таких количествах, чтобы уровни жидкости в среднем колене находились на одной и той же отметке прибора 0.
Затем измеряют высоты стояния жидкостей в трубках над этой отметкой h1 и h2. И имея ввиду, что эти высоты обратно пропорциональны плотностям легко находят плотность исследуемой жидкости.
В случае, когда оба сосуде заполнены одной и той же жидкостью – высоты, на которые поднимется жидкость в сообщающихся сосудах, будут одинаковы. На этом принципе основано устройство так называемого водометного стекла А. Его применяют для определения уровня жидкости в закрытых сосудах, например резервуарах, паровых котлах и т.д.
Принцип сообщающихся сосудов заложен в основе ряда других приборов, предназначенных для измерения давления.
Применение сообщающихся сосудов
Простейшим прибором жидкостного типа является пьезометр, измеряющий давление в жидкости высотой столба той же жидкости.
Пьезометр представляет собой стеклянную трубку небольшого диаметра (обычно не более 5 мм), открытую с одного конца и вторым концом присоединяемую к сосуду, в котором измеряется давление.
Высота поднятия жидкости в пьезометрической трубке – так называемая пьезометрическая высота – характеризует избыточное давление в сосуде и может служить мерой для определения его величины.
Пьезометр – очень чувствительный и точный прибор, но он удобен только для измерения небольших давлений. При больших давлениях трубка пьезометра получается очень длинной, что усложняет измерения.
В этом случае используют жидкостные манометры, в которых давление уравновешивается не жидкостью, которой может быть вода в сообщающихся сосудах, а жидкостью большей плотности. Обычно такой жидкостью выступает ртуть.
Так как плотность ртути в 13,6 раз больше плотности воды и при измерении одних и тех же давлений трубка ртутного манометра оказывается значительно короче пьезометрической трубки и сам прибор получается компактнее.
В случае если необходимо измерить не давление в сосуде, а разность давлений в двух сосудах или, например, в двух точках жидкости в одном и том же сосуде применяют дифференциальные манометры.
Сообщающиеся сосуды находят применение в водяных и ртутных приборах жидкостного типа, но ограничиваются областью сравнительно небольших давлений – в основном они применяются в лабораториях, где ценятся благодаря своей простоте и высокой точности.
Когда необходимо измерить большое давление применяются приборы основанные на механических принципах. Наиболее распространенный из них – пружинный манометр. Под действием давления пружина манометра частично распрямляется и посредством зубчатого механизма приводит в движение стрелку, по отклонению которой на циферблате показана величина давления.
Видео по теме
Ещё одним устройством использующим принцип сообщающихся сосудов хорошо знакомым автолюбителем является гидравлический пресс(домкрат). Конструктивно он состоит из двух цилиндров: одного большого, другого маленького. При воздействии на поршень малого цилиндра на большой передается усилие во столько раз большего давления во сколько площадь большого поршня больше площади малого.
Сообщающиеся сосуды

Всего получено оценок: 1076.
Всего получено оценок: 1076.
Всем известно, что нужно сделать с чайником, чтобы из его носика полилась вода, – просто наклонить. А вот вопрос, можно ли перевести корабль через гору в море или другой водоем, вызовет у нас сомнение. Чтобы ответить на него, сначала следует узнать, что из себя представляют сообщающиеся сосуды.
Закон сообщающихся сосудов
Сообщающиеся сосуды – это взаимодействующие друг с другом сосуды, которые имеют общее дно.
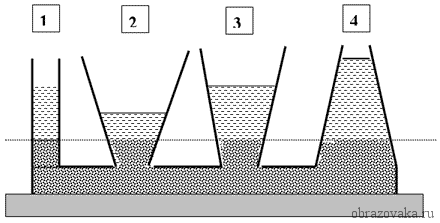
Закон сообщающихся сосудов гласит, что в таких сосудах, какую бы форму они не имели, поверхности однородных жидкостей в состоянии покоя находятся на одном уровне, то есть давление, оказываемое на стенки на любом горизонтальном уровне является одинаковым.
Если же в сосуде жидкости разные, то уровень выше в сосуде, в котором жидкость обладает меньшей плотностью. То есть, если в один сосуд налить жидкость, обладающую одной плотностью, а во второй – другой, то при равновесии их уровни не будут одинаковыми. Следовательно отсюда можно вывести формулу:
Также для сообщающихся сосудов важной является формула:
p=g ρ h
Этой формулой определяется давление жидкости на дно сосуда.
Древним римлянам было неизвестно определение сообщающихся сосудов, поэтому их акведуки – водопроводы занимали огромную протяженность над поверхностью земли и строились с равномерным уклоном вниз.
Свойства сообщающихся сосудов
В сообщающихся сосудах уровень жидкости одинаковый. Это происходит потому, что жидкость производит одинаковое давление на стенки сосуда. Достичь разного уровня однородной жидкости в сообщающихся сосудах можно с помощью перегородки между ними.
Перегородка перекроет сообщение между сосудами, и тогда можно в один из них долить жидкость, чтобы уровень изменился. В данной ситуации возникает напор – давление, производимое весом столба жидкости высотой, равной разности уровней. И если убрать перегородку, то именно это давление станет причиной тому, что жидкость будет перетекать в тот сосуд, где ее уровень ниже, до тех пор, пока уровни не станут одинаковыми.
В жизни очень часто можно встретить естественный напор. И таких примеров довольно много. Например, им обладает вода в горных реках, когда падает с высоты. Плотина также является примером естественного напора. Чем она выше, тем больше будет напор воды, поднятой плотиной.
Применение закона о сообщающихся сосудах
Принцип действия сообщающихся сосудов используется при сооружении фонтанов, водопроводов, шлюзов. Чайник и его носик тоже являются сообщающимися сосудами, так как вода, налитая в чайник, заполняет носик и всю остальную часть до одинаковой высоты. Применение свойств таких сосудов, могут даже помочь провести корабль через гору. И для этого как раз понадобиться шлюз. Шлюз – это лифт для судов. Если водное пространство перегорожено плотиной, то уровень воды в водохранилище выше, чем в реке ниже по течению. И чтобы добраться до этого уровня, судно должно зайти в шлюз, который отгорожен двумя водными непроницаемыми воротами. Когда шлюз полностью заполняется водой, судно выходит из шлюза и продолжает свой путь (уровень воды в шлюзе и водохранилище выравнивается по закону сообщающихся сосудов).

Что мы узнали?
Из этой темы по физики за 7 класс можно ясно понять, какие сосуды называются сообщающимися. Ими могут называться лишь те сосуды, обладающие общим дном, где жидкость может свободно перетекать из одного сосуда в другой. Также сообщающиеся сосуды играют огромную роль в нашей повседневной жизни, облегчая ее и помогая выходить из трудных ситуаций. Принципы сообщающихся сосудов лежат в основе различных чайников, кофейников, водомерных стекол на паровых котлах.
Сообщающиеся сосуды
Цель урока: создать условия для усвоения учащимися понятия о сообщающихся сосудах и их свойстве; повторить закон Паскаля и зависимость давления жидкости от высоты ее столба и плотности. С целью развития кругозора учащихся познакомить их с практическим применением свойства сообщающихся сосудов.
Ход урока
1. Оргмомент
2. Проверка домашнего задания
3. Проверка усвоения ранее изученного материала
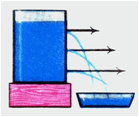
Какой закон проявляется на этом опыте?
Почему вода вытекает из отверстий? Из чего следует, что давление воды увеличивается с глубиной?
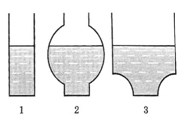
В трех сосудах с одинаковой площадью дна налита вода до одного уровня.
С одинаковой ли силой давит вода на дно этих сосудов?
4. Изучение нового материала
В начале изучения нового материала я хочу продемонстрировать вам небольшой видеофрагмент.
На фоне видеофильма
«Я видел гнев стихии водной.
Себя почуявши свободной,
И широка, и глубока,
Неслася бешено река.
Всё беспощадно сокрушая
И всё ломая на пути –
Живое, мёртвое смывая,
Она неслась, не уставая –
Кто от неё нас мог спасти?»
Два века назад в 1783 году сильное половодье на Москве-реке повредило опоры Большого каменного моста.
По поводу этого происшествия Московский главнокомандующий граф Чернышёв сообщал Екатерине II:
«Обвалились три арки моста и бывшие на них 11 лавок каменных с разными мебелями купца Епанишникова, суммой на 1100 руб. Упал один стоявший в это время на мосту и убит, а развалинами задавлены бывший под мостом рыбак и две женщины, у берега для мытья платья находившиеся».
Итак, москвичи столкнулись с проблемой – наводнения.
Вы сегодня работаете в рабочих листах.
Прочитайте текст, сформулируйте определение понятия «наводнение» и укажите способы, позволяющие предотвратить наводнение.
Физический смысл: поднимается уровень воды.
Но существует еще один способ решения этой проблемы.
Это техническое решение так и осталось с тех пор на карте Москвы. Что это?
Водоотво́дный кана́л (Обводно́й канал, Водоотводно́й канал, Обво́дный канал, Канава)
Действие водоотводного канала основано на принципе действия сообщающихся сосудов. Именно о них и пойдет речь сегодня на уроке.
Запишите в рабочих листах тему урока «Сообщающиеся сосуды».
1. Понятие о сообщающихся сосудах.
Свойства сообщающихся сосудов издревле используются человеком.
Давайте посмотрим фрагмент из известного вам мультфильма.
Видео «Алиса. Чаепитие».
Герои мультфильма пьют чай. И мы каждый день мы пользуемся тем, что вода в чайнике и его носике находится на одном горизонтальном уровне. При медленном наклоне чайника этот уровень не меняется, в результате вода из носика начинает выливаться.
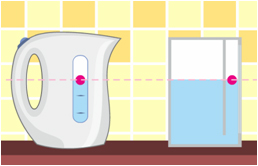
В современных электрических чайниках нет длинного носика, но часто имеется указатель уровня воды, который также представляет собой колено сообщающегося сосуда, в котором плавает на поверхности яркий индикатор.
Сформулируйте определение понятия «сообщающиеся сосуды».
Сообщающиеся сосуды – это сосуды, соединенные между собой трубкой.
Научное открытие сообщающихся сосудов датируется 1586 годом (голландский ученый Симон Стевин), но, судя по устройству священной неиссякаемой чаши, оно было известно еще жрецам Древней Греции.
2. Свойство сообщающихся сосудов
Демонстрационный опыт «Сообщающийся сосуд» (Проводит ребенок под руководством учителя – комментировано).
Задание. Установите зависимость формы и сечения сообщающегося сосуда и уровня поверхности однородной жидкости. Подчеркните верный ответ.
Для этого заполним сообщающийся сосуд водным раствором перманганата калия (KMnO4).
Вывод: в сообщающихся сосудах любой формы и сечения поверхности однородной жидкости устанавливаются на (разных уровнях/одном уровне).
3. Зависимость высоты столба жидкостей от их плотностей
Физика – наука экспериментальная. Физический эксперимент может выполнять двойственную функцию: во-первых, служит источником нового знания, во-вторых, подтверждает или опровергает имеющееся суждение.
Работа в группах (по рядам) (Фоновая музыка)
Группа 1
Группа 2
Однородные жидкости
Разнородные жидкости
Задание: используя формулу давления жидкости на дно сосуда, установите, как зависит высота столба однородных жидкостей от их плотности.
Экспериментально подтвердите полученный вывод.
Задание: проделайте интерактивный опыт (стр. 7), который покажет, как установятся уровни жидкости в сообщающихся сосудах, если в них налить разнородные жидкости. Объясните полученные результаты, используя формулу давления жидкости на дно сосуда.
Жидкость покоится, не перемещается из одного сосуда в другой, значит, давления ее в обоих сосудах на любом уровне одинаковы.
h1 = h2;
Если же в одни из этих сосудов налить одну жидкость ρ 1, а в другую — другую жидкость ρ 2, то уровни этих жидкостей окажутся разными. Однако поскольку жидкости и в данном случае будут покоиться, то давление создаваемое обоими столбами жидкостей равны.
Т.к. r1 > r2, то h1
Сообщающиеся сосуды
Жидкое агрегатное состояние
Давайте для начало разберемся, как ведет себя жидкость в различных сосудах.
В мире есть три агрегатных состояния: твердое, жидкое и газообразное.
Их характеристики — в таблице:
Агрегатные состояния
Свойства
Расположение молекул
Расстояние между молекулами
Движение молекулы
сохраняет форму и объем
в кристаллической решетке
соотносится с размером молекул
колеблется около своего положения в кристаллической решетке
близко друг к другу
малоподвижны, при нагревании скорость движения молекул увеличивается
занимают предоставленный объем
больше размеров молекул
хаотичное и непрерывное
В этом состоянии сохраняется объем, но не сохраняется форма. Например, если перелить молоко из кувшина в стакан — молоко, имевшее форму кувшина, примет форму стакана. Кстати, в корове у молока тоже была другая форма.
Расстояние между молекулами в жидком состоянии чуть больше, чем в твердом, но все равно невелико. При этом частицы не собраны в кристаллическую решетку, а расположены хаотично. Молекулы почти не двигаются, но при нагревании жидкости делают это более охотно.
Вспомните, что происходит, если залить чайный пакетик холодной водой — он почти не заваривается. А вот если налить кипяточку — чай точно будет готов.
Агрегатных состояния точно три?
На самом деле, есть еще четвертое — плазма. Звучит, как что-то из научной фантастики, но это просто ионизированный газ — газ, в котором помимо нейтральных частиц, есть еще и заряженные. Ионизаторы воздуха как раз строятся на принципе перехода из газообразного вещества в плазму.
Сообщающиеся сосуды
Поскольку жидкость принимает форму сосуда, в который ее поместили, имеет место быть такое явление, как сообщающиеся сосуды.
Какую бы форму не имели такие сосуды, на поверхности однородных жидкостей в состоянии покоя на одном уровне действует одинаковое давление.
Если в колена сообщающихся сосудов налить жидкости, плотности которых будут различны, то меньший объём более плотной жидкости в одном колене уравновесит больший объём менее плотной жидкости в другом колене сосуда.
Другими словами, высота столба жидкости с меньшей плотностью больше, чем высота столба жидкости с большей плотностью. Давайте рассчитаем, во сколько высота столба жидкости с меньшей плотностью больше высоты столба жидкости с большей плотностью, если эти две несмешивающиеся жидкости находятся в сообщающихся сосудах.
Применение сообщающихся сосудов
На принципе сообщающихся сосудов основано устройство очень простого прибора для определения плотности жидкости. Этот прибор состоит из двух сообщающихся сосудов: двух вертикальных стеклянных трубок, соединенных между собой третьей изогнутой трубкой.
Одна из вертикальных трубок заполняется жидкостью, плотность которой нужно определить, а другая — жидкостью известной плотности (например, водой, плотность которой равна 1000 кг/м^3). Жидкости должны заполнить трубки настолько, чтобы их уровень в изогнутой трубке посередине был на отметке прибора 0. Высоты жидкостей в трубках над этой отметкой измеряют и находят плотность исследуемой жидкости, зная, что высоты обратно пропорциональны плотностям (об этом мы говорили выше).
Также на законе сообщающихся сосудах основаны устройства, которые определяют уровень жидкости в закрытых сосудах: резервуарах, паровых котлах.
Чтобы судно могло переплыть из одной водного бассейна в другой, если уровни воды в них разные, необходимо использовать шлюз. Устройство шлюза также основано на принципе сообщающихся сосудов. В первых воротах шлюза открывается клапан, камера соединяется с водоёмом, они становятся сообщающимися сосудами, уровни воды в них выравниваются. После этого ворота открываются, и судно проходит в первую камеру. Открывается следующий клапан, после выравнивания уровней воды открываются ворота, и так повторяется столько раз, сколько камер имеет шлюз.
Давление столба жидкости
Выведем формулу давления столба жидкости через основную формулу давления.
Давление
p = F/S
В случае давления жидкости на дно сосуда мы можем заменить силу в формуле на силу тяжести.
Также мы можем представить массу жидкости, как произведение плотности на объем:
Из геометрии мы знаем, что объем тела вращения (например, цилиндра) — это произведение площади основания на высоту: V = Sh.
Следовательно, высота будет равна h = V/S. Подставляем в формулу высоту вместо отношения объема к площади.
В сообщающихся сосудах давление жидкости на одном уровне (на одной и той же высоте) будет одинаковым.
А можно сделать так, чтобы давление было разным?
С помощью перегородки можно сделать так, чтобы уровень жидкости, а следовательно, и давления в сообщающихся сосудах отличались.
Перегородка, установленная между сосудами перекроет сообщение. Далее доливая жидкость в один из сосудов мы создаем дополнительное давление. Если затем убрать перегородку, то жидкость начнет перетекать в тот сосуд, где её уровень ниже — до тех пор, пока высота жидкости в обоих сосудах не станет одинаковой.
Этот принцип используют в водонапорной башне. Чтобы создать высокое давление, башню наполняют водой. Затем открывают трубы на нижнем этаже, и вода устремляется в дома в наши краны и батареи.
Задачка
Какой площади необходимо сделать малый поршень в гидравлическом прессе, для того, чтобы выигрыш в силе получился равным 2? Площадь большого поршня равна 10 см^2.
Решение:
Гидравлический пресс — это два цилиндрических сообщающихся сосуда. Площадь большого поршня, с приложенной силой F1, равна 10 см^2.
Площадь малого поршня обозначим Sмал, к нему приложена сила F2.
Давления в сообщающихся сосудах на одинаковой высоте равны: p1 = p2
Подставим формулу давления:
F1/Sбол=F2/Sмал.
Выразим Sмал, получим:
Так как по условию выигрыш в силе F2/F1 равен 2, то:
Sмал=2*Sбол= 2*10 = 20 см^2
Ответ: малый поршень необходимо сделать с площадью равной 20 см^2