что такое согласованный фильтр

Сравнение методов распознавания сигналов. Нейронные сети против согласованного фильтра

Я недавно опубликовал статью «Распознавание радиотехнических сигналов с помощью нейронных сетей»[1]. И там была довольно длинная и интересная дискуссия по поводу возможности использования для этих целей согласованного фильтра(СФ). Разумеется, использовать согласованные фильтры для той задачи, что решалась, проблематично. Но меня заинтересовал другой вопрос, что лучше использовать при незначительных колебаниях параметров сигнала, нейронные сети(НС) или СФ. В качестве генератора сигнала буду использовать обычный мультивибратор. Подавать сигнал буду через звуковую карту, а далее распознавать с помощью метода описанного в [1] и с помощью согласованного фильтра. Далее ПО сравнит результаты и даст ответ какой метод лучше.

Часть 1. Генератор сигнала

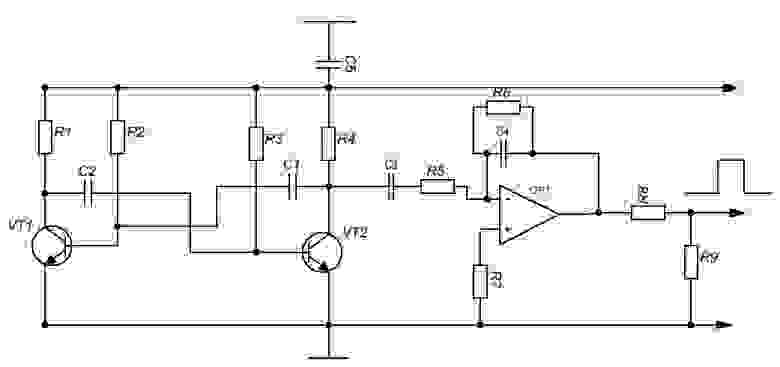
Для того чтобы сравнение было адекватным, будем распознавать РЕАЛЬНЫЙ сигнал. Для его создания нужен генератор. Так же понадобится генератор шума. Сигнал будем генерировать с помощью мультивибратора. И чтобы «не лезли» ВЧ составляющие на выход надо поставить ФНЧ. Питание осуществляется от USB. Диапазон подаваемого напряжения на аудио карту должен быть в пределах 0.001 — 1.5В. А выход с мультивибратора лежит от 0 до 5В. Для ограничения напряжения будем использовать Г-образный делитель. Ниже представлена принципиальная схема генератора.

Делать с нуля я его не стал, т.к. на втором курсе, в рамках хакатона, собирал предусилитель кардиосигнала для съема кардиоинтервалограммы, который отличается только отсутствием ПОС между двумя каскадами. Поэтому я ограничился добавлением этой связи. Вот что в итоге получилось.

В качестве генератора белого шума, я использовал метод randNorm из своей мат. библиотеки AI.MathMod для языка C#.

Часть 2. Прием сигнала

Для приема и записи сигнала я использовал библиотеку NAudio для языка C#. Далее надо создать класс для записи сигнала. В начале подключаем пространства имен.

Объявляем глобальные переменные:

И метод для начала записи (взято отсюда):

Часть 3. Согласованный фильтр

Теперь надо создать модель согласованного фильтра. Согласованный фильтр(СФ) обеспчивает максимальное ОСШ(отношение сигнал/шум) в случае если фильтр согласован с полезным сигналом, т.е. АЧХ фильтра совпадает с модулем спектральной плотности сигнала. Состоит СФ из согласованного фильтра для одиночного импульса(СФОИ), линий задержки(ЛЗ) и сумматора. СФОИ для прямоугольного импульса состоит из интегратора, ЛЗ, инвертора и сумматора(для радио импульса с прямоугольной огибающей интегратор заменен на радиоинтегратор, в качестве которого часто выступает полосовой фильтр, в частности колебательный контур или резонансный усилитель с колебательным контуром в коллекторной цепи). Ниже представлена структурная схема. Увеличение ОСШ происходит благодаря тому, что сигнал узкополосный, а помеха широкополосная.[2]

Так же накопитель дает увеличение ОСШ в раз, где m количество импульсов в пачке. Из-за дороговизны и сложности реализации ЛЗ, в реальных задачах все чаще используют метод с цифровым накоплением. Тогда вероятность ложной тревоги и верного обнаружения задаются следующими соотношениями:

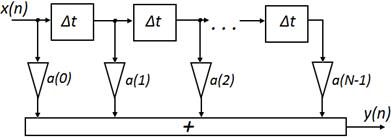
Структура накопителя(все коеф. «а» = 1):

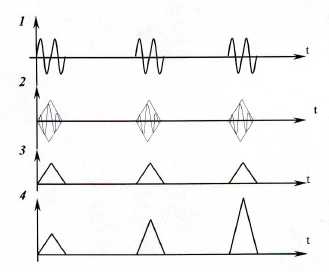
Схематично работа накопителя представлена ниже:

Из-за того что периоды следования импульсов равны как и длительности импульсов, можно использовать вместо набора линий задержек только одну, поставить так называемый рециркулятор с накопителем.[3]

В нашем случае идеальный, без потерь. Структурная схема СФ.

Подробнее о структуре и расчетах СФ можете почитать в [2 стр. 415 — 427] и [3 стр. 563 — 598].

При вероятности нахождения там сигнала >0.6 принимается решение, что сигнал зарегистрирован.

Часть 4. ПО для сравнения

Архитектура программы в своей структуре содержит «два флажка»,

при старте программы они оба неактивны, имеется метод, который каждый раз, как опрашивается окно проверяет активны ли флажки, если активен первый флажок зачисляется 1 балл согласованным фильтрам. Если же второй, то балл зачисляется нейронной сети. В любом случае все параметры возвращаются в исходное положение.

Итог

Было проведено 20 экспериментов, в которых использовался, согласованный фильтр настроенный на исследуемый сигнал, ОСШ = 0.4, результат: 16:4 в пользу СФ. После чего была изменена длительность сигнала на 5%, результат: 2:18 в пользу НС. Из этого можно сделать вывод, что при ИЗВЕСТНЫХ параметрах СФ работает намного лучше чем ИНС, но когда параметры не известны, или могут варьироваться, целесообразней использовать ИНС.

Литература:

Источник

Что такое согласованный фильтр

Основные принципы согласованной фильтрации были сформулированы в результате исследований, направленных на оптимизацию функционирования радиолокационных систем. По этим углубленным теоретическим представлениям необходимо было разработать схемы, которые могли бы быть реализованы инженерами-практиками. Метод согласованной фильтрации осуществляет оптимальную

линейную обработку радиолокационных сигналов. При такой обработке исходная радиолокационная информация, поступающая на вход приемника и искаженная согласно предположению белым гауссовым шумом, преобразуется к виду, удобному для вынесения оптимального решения об обнаружении (наличия или отсутствия цели) или для оценки параметров цели (дальности, скорости и т. д.) с минимальной среднеквадратичной ошибкой, или для обеспечения максимально возможного разрешения группы целей.

Характеристики согласованных фильтров могут быть описаны. с помощью частотной либо временной функции отклика, которые связаны между собой преобразованием Фурье. В пространстве частот переходная функция согласованного фильтра есть комплексно-сопряженная функция спектра сигнала, который должен быть обработан оптимальным образом. Таким образом в общем виде

где спектр входного сигнала постоянная задержка, нужная для физической реализации фильтра. Нормирующий коэффициент и постоянная задержка, как правило, опускаются при записи основных соотношений теории согласованной фильтрации, которые обычно формулируются в виде

Соответствующая зависимость во временной области между сигналом, который должен быть обработан, и характеристикой согласованного фильтра получается в результате обратного преобразования функции Фурье Это приводит к тому, что импульсный отклик фильтра представляет собой обращенную во времени копию известной временной функции, описывающей сигнал. Таким образом, если импульсный отклик согласованного фильтра есть то основное соотношение, эквивалентное равенству (1.2), имеет вид

Как и в предыдущем случае, произвольная задержка в записи основного соотношения может быть опущена:

Считается, что свойства оптимального приемника в зависимости от параметров спектра сигнала для случая белого гауссового шума [уравнение (1.2)] первым определил Норе 151. Поэтому согласованные фильтры называют также фильтрами Норса; однако Ван Флек и

Миддлтон [6] были, очевидно, первыми, кто использовал термин «согласованный фильтр» по отношению к фильтрам, оптимизирующим отношение сигнал/шум для импульсных сигналов. Вывод требований, которым должен удовлетворять согласованный фильтр, рассматривается в гл. 2 для законченности изложения, а также с тем, чтобы помочь заинтересованному читателю глубже понять сущность систем с согласованными фильтрами. На рис. 1.2 иллюстрируются соотношения, определяемые равенствами (1.3) и (1.5).

Рис. 1.2. Связь между характеристиками сигнала и согласованного фильтра.

Исходные соображения для вывода условий, определяющих оптимальное обнаружение сигнала, поясняются на рис. 1.3, где дана упрощенная схема приемной системы. Выходной сигнал в точке представляет собой смесь сигнала с шумом. Целью разработчика системы являетсй оптимизация вероятности обнаружения сигнала на некотором интервале наблюдения, который может представлять собой строб дальности. В других случаях этот интервал явно не указан, мы просто фиксируем факт, что внимание наблюдателя должно быть направлено на некоторую особую точку случайно либо вследствие наличия априорных данных. Порог наблюдения может быть четко зафиксированным, например, в автоматических сигнализаторах тревоги, или устанавливаться подсознательно человеком-оператором, который по своим физиологическим свойствам способен не учитывать даже сравнительно большие шумовые выбросы, не являющиеся истинными сигналами. Статистические характеристики, используемые в процессе обнаружения, будут зависеть от многих факторов, например от уровня порога и наличия априорной информации относительно расположения сигнала.

Однако даже без учета существенных факторов из рассмотрения рис. 1.3 мы можем заметить, что для. оптимизации процедуры обнаружения, как подсказывает логика, следует попытаться максимизировать пиковое значение сигнала по отношению к шуму. Так как сигнал, по всей вероятности, присутствует редко (непрерывный сигнал по определению не может переносить полезной информации), то при непрерывном наблюдении случайных флюктуаций шумового сигнала мы будем концентрировать внимание на кратковременных отклонениях от усредненного за длительный период или среднеквадратичного значения шума.

Рис. 1.3. Критерий обнаружения сигнала.

С этой точки зрения логично сделать вывод, что получение максимального пикового значения сигнала по отношению к среднеквадратичному значению шума будет приводить к нужной нам оптимизации, т. е.

Читатель, которого интересует определение условий максимизации отношения, задаваемого равенством (1.6), может найти этот вывод в гл. 2, где рассматривается также статистический подход к оптимизации характеристик систем обнаружения. Оба эти подхода приводят к целесообразности использования согласованной фильтрации, которая характеризуется равенствами (1.3) и (1.5). Найдено, что в случае применения согласованного фильтра, который задается этими выражениями, максимальное значение отношения сигнал/шум на выходе фильтра при наличии белого гауссова шума определяется соотношением

Равенство (1.7) для простого импульсного радиолокационного сигнала может быть получено эвристическим путем при

рассмотреции параметров, показанных на рис. 1.4. Энергия принимаемого сигнала равна

а мощность шума определяется как

где спектральная плотность мощности шума и эффективная полоса фильтра.

Рис. 1.4. Параметры импульсного сигнала.

Отношение Пиковой мощности сигнала к мощности шума, выраженное через энергию сигнала, равно

Для получения равенств, описывающих оптимальную обработку, можно использовать известный вывод о том, что ширина полосы фильтра связана с длительностью импульса приближенной зависимостью

где значение всегда близко к единице. Предположим, что тогда отношение сигнал/шум, задаваемое равенством (1.10), сведется к

Этот результат означает для разработчика радиолокатора, что «поскольку согласованный фильтр используется в додетекторных

каскадах приемной системы, то ее способность к обнаружению зависит только от содержащейся в сигнале энергии и никоим образом не связана с формой сигнала, в которой он поступает на вход приемника. Для того чтобы получить оптимальное отношение сигнал/шум на выходе, фильтр должен быть согласован с сигналом. Однако теория показывает, что если построение строго согласованного фильтра окажется практически невыгодным или невозможным, то обычно можно использовать разумную аппроксимацию, причем это весьма слабо скажется на способности радиолокационной системы к обнаружению сигнала.

Источник

Согласованный фильтр его импульсная и частотная характеристики

В предыдущей статье рассмотрели оптимальный прием сигналов и ансамбль сигнала. В этой статье поговорим о согласованном фильтре, его свойствах и АЧХ и ФЧХ характеристиках.

Согласованный фильтр

Согласованный фильтр — линейный оптимальный фильтр, позволяющий получить максимальное отношение сигнал/шум на выходе фильтра для сигналов известной формы.

Линейный фильтр вносит линейные искажения. Если на нелинейное устройство подать моногармонический сигнал (обычную синусоиду) с одной частотой, то на выходе устройства, посмотрев на спектр, увидим новые спектральные составляющие, гармоники. У линейного устройства новые спектральные составляющие не появляются. На выходе любого линейного устройства, те же самые спектральные составляющие, что и на его входе, без добавления новых гармоник, у этих устройств изменяются только амплитуда и фаза.

Оптимальный фильтр, оптимальный это значит, что он достигает какого-то наилучшего качества. Если мы говорим про оптимальность, то мы должны говорить и про критерий оптимальности, т.е. что у нас достигается наилучшим способом. В данном случае критерием оптимальности является отношение сигнал/шум.

Для каждого сигнала существует свой согласованный фильтр. Сигнал на выходе любого линейного фильтра, в том числе и согласованного, определяется выражением:

Свойства согласованного фильтра

Для любого линейного фильтра сигнал на выходе определяется через свертку сигнала на входе и его импульсной характеристики.

Импульсная характеристика фильтра это реакция фильтра (т.е. то что мы получим на выходе фильтра), на дельта импульс.

Если на вход фильтра подадим дельта импульс, то на выходе получим отклик, этот отклик и есть импульсная характеристика.

Дельта импульс это математическая абстракция, это импульс, который имеет бесконечно большую амплитуду, бесконечно малую длительность и площадь этого импульса равна единице. На практике, такой дельта импульс можно заменить коротким импульсом. Спектр дельта импульса равномерен и бесконечен.

Импульсная характеристика согласованного фильтра

Импульсная характеристика СФ имеет отзеркаленную форму сигнала, для которого фильтр согласован:

Не важно какую амплитуду имеет сигнал, если по форме сигнал повторяет импульсную характеристику, то фильтр будет согласован для этого сигнала. На картинке ниже представлено два примера. Есть треугольный сигнал, осциллограмма в виде треугольного импульса.

Какой фильтр будет для него согласован? Тот который имеет импульсную характеристику повторяющую форму сигнала, но отзеркаленную.

Другой пример, выше, затухающая синусоида сигнала. Чтобы спроектировать согласованный фильтр для такого сигнала, нужно взять форму сигнала и отзеркалить ее и получится импульсная характеристика.

Если у сигнала меняется амплитуда, становится больше или меньше, импульсная характеристика не меняется, фильтр всё равно будет согласован.

Частотные характеристики согласованного фильтра

Комплексная частотная передаточная характеристика СФ комплексно сопряжена с Фурье-образом сигнала.

Комплексная экспонента е^-i2πTf говорит о сдвиге фаз, возникшем в результате задержки сигнала в фильтре на время T. Откуда взялась комплексная экспонента? Любой фильтр вносит задержку, а комплексная экспонента поворачивает фазу сигнала.

Эта функция H(f) комплексная, у нее есть мнимая и реальная части. Формула с точностью до постоянного множителя (константы) повторяет Фурье-образ сигнала S(f). Единственное, нужно взять Фурье-образ и сделать над ним комплексное сопряжение. Фурье-образ сигнала это результат преобразования Фурье. Это комплексный спектр сигнала.

Комплексная частотная передаточная характеристика СФ комплексно сопряжена с Фурье-образом сигнала с точностью до какого-то постоянного коэффициента. Импульсная характеристика повторяет форму сигнала, частотная характеристика повторяет спектр сигнала, только комплексно сопряжена.

Комплексное сопряжение. Если есть комплексное число в котором есть реальная и мнимая часть, то комплексное число сопряженное, это число у которого меняется знак мнимой части. c=a+jb и c=a-jb.

АЧХ и ФЧХ согласованного фильтра

Из передаточной характеристики H(f) получаем АЧХ и ФЧХ. Чтобы получить АЧХ нужно у этой функции взять модуль. АЧХ согласованного фильтра с точностью до постоянного коэффициента k повторяет амплитудный спектр сигнала:

ФЧХ согласованного фильтра повторяет фазовый спектр сигнала с обратным знаком и с учетом задержки:

где ψs(f) — фазовый спектр сигнала.

На картинке выше есть амплитудный и фазовый спектр. Чтобы получить согласованный фильтр, нужно взять фильтр, который имеет АЧХ повторяющий амплитудный спектр сигнала и ФЧХ повторяющий фазовый спектр сигнала, но с обратным знаком. Наклон, который появился на графике “ФЧХ согласованного фильтра” появился из-за задержки сигнала.

Отклик согласованного фильтра

Предположим, есть сигнал, который имеет прямоугольную форму, для него спроектирован согласованный фильтр, который будет иметь импульсную характеристику в виде прямоугольного импульса.

Если на вход согласованного фильтра подать прямоугольный импульс, то на выходе получится сигнал, который определяется через свёртку.

Свёртка это перемножение двух функций в различный момент сдвига друг относительно друга и затем функции нужно их проинтегрировать.

На картинке, зафиксировали положение импульсов. Есть один импульс s(t) на входе и вторая импульсная характеристика согласованного фильтра h(t). В конкретный момент времени нужно вычислить площадь, которая образуется пересечением и эта площадь — значение сигнала на выходе в какой-то конкретный момент времени. И нужно постепенно смещать этот импульс и снова вычислять площадь и так далее. В итоге получим функцию, это и есть свертка.

Сигнал проходя через согласованный фильтр не сохраняет свою форму.

С точки зрения приема сигнала важна не его форма, а значение сигнала. В следующей статье расскажем про приемники.

Источник

Согласованная фильтрация типовых широкополосных сигналов

Изготовление аналоговых согласованных фильтров, особенно для сложных энергоёмких сигналов, сложно и не допускает перестройки их параметров. Поэтому компьютерное моделирование, в частности в пакете прикладных программ MATLAB, позволяет изучать особенности согласованной обработки сигналов и реакцию согласованного фильтра на входное воздействие.

В публикации рассматривается опыт создания и использования програмных продуктов в среде MATLAB при проведении занятий с обучающимися по дисциплине «Радиотехнические системы».

Оптимальная временная обработка сигнала, принимаемого на фоне стационарного белого шума, сводится к вычислению корреляционного интеграла. Это выражение аналогично интегралу свёртки, который описывает реакцию линейного фильтра с импульсной характеристикой на принимаемый сигнал. Эта аналогия позволяет использовать для вычисления корреляционного интеграла линейный фильтр, импульсная характеристика которого согласована с ожидаемым сигналом. При приёме сигнала на фоне стационарного белого шума импульсная характеристика согласованного фильтра (СФ) зеркальна по отношению к ожидаемому сигналу. Согласованный фильтр является оптимальным устройством обработки входной реализации с точки зрения получения максимального отношения сигнал-шум.

Изготовление аналоговых согласованных фильтров, особенно для сложных энергоёмких сигналов, сложно и не допускает перестройки их параметров. Поэтому компьютерное моделирование, в частности в пакете прикладных программ MATLAB, позволяет изучать особенности согласованной обработки сигналов и реакцию согласованного фильтра на входное воздействие.

Рис.1. Структурная схема оптималного обнаружителя сигнала со случайными параметрами

Практическое занятие «Согласованная фильтрация типовых широкополосных сигналов» учебной дисциплины «Радиотехнические системы» проводится методом решения задач по оценке выходного эффекта при прохождении ЛЧМ и ФКМ радиоимпульса через устройства оптимальной обработки с помощью программ.

Для обеспечения данного вида занятия были разработаны программы в ППП MATLAB с простым пользовательским интерфейсом (UI) (рис.2.).

Рис.2. Окно среды GUIDE

Ниже приведена ссылка.

Дальнейшая компиляция продукта осуществляется с помощью встроеных приложений (рис.3).

Рис.3. Окно компилятора Matlab

При отработке первого вопроса занятия используется программа «Имитационная модель исследования согласованной обработки ЛЧМ сигналов».

Рис.4. Свидетельство о государственной регистрации программ для ЭВМ

Рис.5. Внешний вид окна программы «Имитационная модель исследования согласованной обработки ЛЧМ сигналов»

При рассмотрении первого вопроса особое внимание уделяется выработке у обучающихся практических умений в расчете коэффициента сжатия ЛЧМ сигнала на выходе устройства оптимальной обработки и оценке систематической ошибки измерения времени запаздывания.

В развернувшемся рабочем окне в поле «Зондирующий сигнал» вводятся параметры зондирующего сигнала. Для обработки сигнала с заданными параметрами необходимо нажать кнопку «Расчет» (рис.6).

Рис.6. К пояснению порядка работы в окне программы

После нажатия кнопки «Расчет» запускается процесс моделирования прохождения сигнала с заданными параметрами через согласованный фильтр.

Рис.7. К пояснению эффекта сжатия сигнала и процесса измерения информативного параметра сигнала

Определение ошибки измерения времени запаздывания находится как разность между истинным временем запаздывания, которое соответствует случаю нулевой частотной расстройки и измеренным значением.

При отработке первого вопроса занятия используется программа «Имитационная модель исследования согласованной обработки ФКМ сигналов, манипулированных по коду Баркера».

Рис.8. Свидетельство о государственной регистрации программ для ЭВМ

В ходе отработки второго вопроса занятия уделяется внимание обучающихся на форму ФКМ сигнала и величину уровня боковых лепестков на выходе устройства оптимальной обработки.

1. В развернувшемся рабочем окне во вкладке «Зондирующий сигнал» во всплывающем списке необходимо выбрать код Баркера входного (исследуемого) сигнала.

Рис.9. Внешний вид окна программы «Имитационная модель исследования согласованной обработки ФКМ сигналов,манипулированных по коду Баркера»

2. В окне «Значение кода импульсной характеристики» задается код импульсной характеристики согласованного фильтра.

Рис.10. К пояснению порядка работы в окне программы

3. После нажатия кнопки «Расчёт» запускается моделирование процесса прохождения сигнала через фильтровое устройство оптимальной обработки (рис.1). Полученные реализации входного сигнала, импульсной характеристики фильтра и сигнала на выходе СФ обучающиеся зарисовывают в рабочих тетрадях.

Рис.7. К пояснению процесса обработки ФКМ сигнала

4. Рассчитается коэффициент сжатия.

5. Оценивается отношение амплитуды боковых лепестков АКФ по отношению к главному.

6. В окне «Значение кода импульсной характеристики» задается значение, отличное от кода Баркера (в любом из дискрет импульсной характеристики меняется код на обратный). После процесса моделирования по графикам оценивается изменение временной структуры сигнала на выходе фильтра. Рассчитывается значение коэффициента сжатия.

7. Сравниваются значения коэффициентов сжатия, рассчитанных в пунктах 4 и 6.

8. Определяются ошибки измерения времени запаздывания при несогласованной обработке сигнала.

Источник