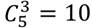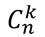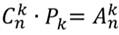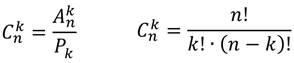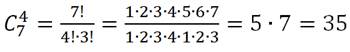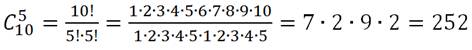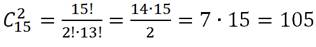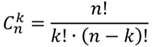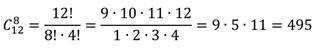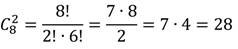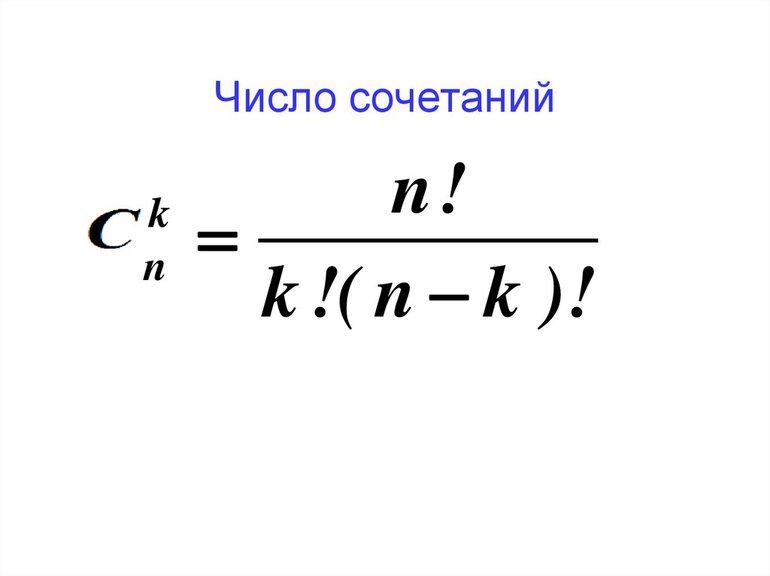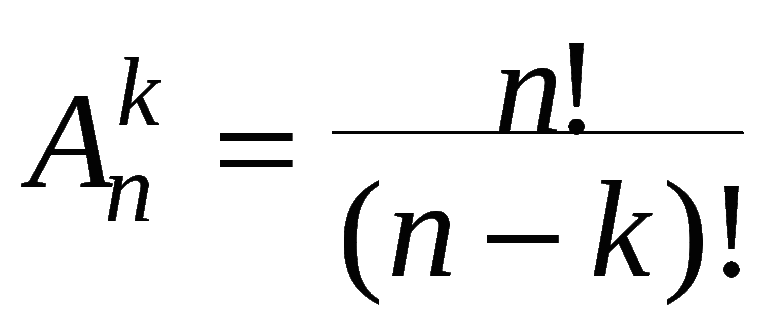что такое сочетание в математике

1.3.3. Сочетания

В учебниках обычно даётся лаконичное и не очень понятное определение сочетаний, поэтому в моих устах формулировка будет не особо рациональной, но, надеюсь, доходчивой:

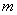
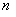
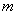
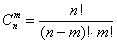
Сочетаниями называют различные комбинации из объектов, которые выбраны из множества различных объектов, и которые отличаются друг от друга хотя бы одним объектом. Иными словами, отдельно взятое сочетание – это уникальная выборка из элементов, в которой не важен их порядок (расположение). Общее же количество таких уникальных сочетаний рассчитывается по формуле .
Задача 3

В ящике находится 15 деталей. Сколькими способами можно взять 4 детали?

Решение: прежде всего, обращаю внимание на то, что по логике такого условия, детали считаются различными – даже если они на самом деле однотипны и визуально одинаковы (в этом случае их можно, например, пронумеровать
).

В задаче речь идёт о выборке из четырёх деталей, в которой не имеет значения их «дальнейшая судьба» – грубо говоря, «просто выбрали 4 штуки и всё». Таким образом, у нас имеют место сочетания деталей. Считаем их количество:

(прерываю решение для промежуточных объяснений)

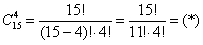
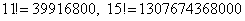
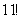
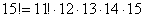
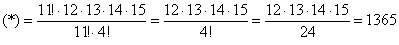
И здесь, конечно, не нужно «тягать» значения . В похожей ситуации я советую использовать следующий приём: в знаменателе выбираем наибольший факториал (в данном случае ) и сокращаем на него дробь. Для этого числитель следует представить в виде . Распишу очень подробно:

способами можно взять 4 детали из ящика.

Ещё раз: что это значит? Это значит, что из 15 различных деталей можно составить одну тысячу триста шестьдесят пять уникальных сочетаний из 4 деталей. То есть, каждая такая комбинация из четырёх деталей будет отличаться от других комбинаций хотя бы одной деталью.

Ответ: 1365 способами

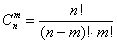
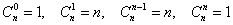
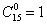
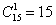
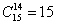
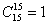
Формуле необходимо уделить самое пристальное внимание, поскольку она является «хитом» комбинаторики. При этом полезно понимать и без всяких вычислений записывать «крайние» значения: . Применительно к разобранной задаче:

– единственным способом можно не выбрать ни одной детали;
способами можно взять 1 деталь (любую из 15);
способами можно взять 14 деталей (при этом какая-то одна из 15 останется в ящике);
– единственным способом можно выбрать все пятнадцать деталей.

Рекомендую вновь обратиться к Приложению Формулы комбинаторики и внимательно ознакомиться с биномом Ньютона и треугольником Паскаля (пункт 3), по которому очень удобно выполнять проверку вычислений количества сочетаний 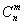при небольших значениях «эн».

Для самостоятельного решения:

Задача 4

а) Сколькими способами из колоды в 36 карт можно выбрать 3 карты?

б) В шахматном турнире участвует 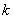человек и каждый с каждым играет по одной партии. Сколько всего партий сыграно в турнире?

Чем приятны многие комбинаторные задачи, так это краткостью – главное, разобраться в сути. Решения и ответы в конце книги.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Источник

Сочетания и размещения — что это такое и в чем разница

Оба этих понятия – сочетание и размещение – относятся к науке комбинаторике. Это раздел математики, созданный учеными Б. Паскалем и П. Ферма в процессе исследования теории карточных игр. Комбинаторика используется в решении задач особенного рода: когда требуется вычислить количество потенциальных вариантов для какой-либо ситуации. Примером может служить подсчет возможных позиций на шахматной доске после первого хода «черных» и «белых».

О сочетании и размещении говорят, когда из множества необходимо выбрать какое-либо подмножество. Понятия эти весьма близки по своему смыслу, поэтому так трудно бывает понять разницу между ними. Но она существует (причем принципиальная!). Ниже об этом достаточно простым языком написано в статье.

Сочетания

Сочетание – это подмножество, состоящее из К элементов, выбранных из множества, включающего в себя N элементов. При этом выполняется такое условие: N > К.

Важный момент: порядок расположения в данной выборке никакого значение не имеет. То есть комбинации, отличающиеся порядком размещения элементов, но не составом, считаются одинаковыми сочетаниями.

Образно проиллюстрировать понятие можно на примере лотереи. Предположим, человеку предлагается угадать 3 выпавшие цифры из 15-ти. Он выбрал следующий набор – 1, 6, 10. И уже не важно, в каком порядке они выпадут: 1, 6, 10; 1, 10, 6; 10, 1, 6; 10, 6, 1; 6, 10, 1; 6, 1, 10. Главное – состав комбинации. Если он совпадает с загаданным накануне набором цифр, игрок считается победителем.

Сочетания обозначаются следующим образом: С К _N. Где N – количество элементов в множестве, а К – количество объектов в производимой выборке. Для нашего примера N = 15, а К = 3.

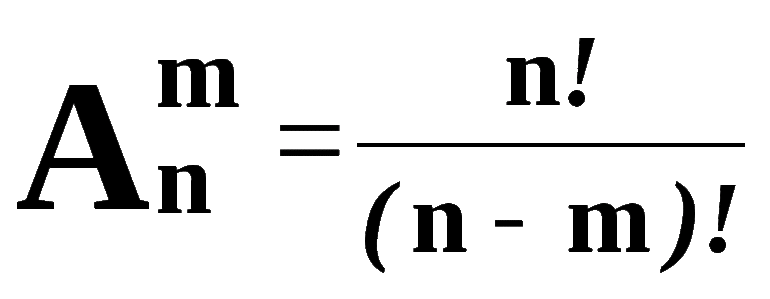
Существует формула для определения числа возможных сочетаний в множестве. Выглядит она так: N!/((N-K)!*K!) подставим цифры из нашего примера:

Это означает, что из 15 чисел можно составить 455 различных комбинаций, включающих в себя три разных числа.

Такие подсчеты в нашем примере позволяют определить велики ли шансы субъекта на выигрыш.

Размещения

В самом названии этого термина присутствует корень, позволяющий понять его суть. Размещение – тоже подмножество, выбранное из первоначального множества. Но здесь уже существенное значение имеет место расположения элемента в комбинации. То есть если сочетания могут различаться только составом объектов, то размещения разнятся и составом, и порядком следования элементов.

Получается, что количество размещений всегда превосходит число сочетаний, при условии выборки из одного и того же множества.

Это легко проследить, если сделать выборку трех элементов из множества, состоящего всего из 4 объектов (от 1-го до 4-х).

Сочетаний здесь будет всего 4 (это легко проверить и по приведенной выше формуле):

Размещений же окажется гораздо больше:

123, 132, 321, 312, 231, 213, 234, 243, 324, 342 и т.д.

Существует формула, позволяющая подсчитать возможное количество размещений в представленном множестве:

Для нашего примера посчитаем количество потенциальных размещений:

Получается, что для состоящего из 4-х элементов множества существует 4 сочетания и целых 24 размещения.

Для тех, кто увлекается спортивными ставками, эти знания могут пригодится для того, чтобы рассчитать шансы на выигрыш.

Например, в турнире участвует 6 команд. Необходимо определить количество возможных комбинаций троек призеров кубка.

Обозначим названия команд буквами: А, Б, В, Г, Д, Е.

Сначала определим команду, которая станет золотым призером чемпионата. Таких вариантов, очевидно, 6: А, Б, В, Г, Д, Е.

Затем выбираем один из вариантов (пусть это будет комбинация, в которой золото принадлежит команде А), и определяем для него потенциального серебряного призера. Таких комбинаций уже окажется всего 5, так как одна команда уже записана на 1-м месте: АБ, АВ, АГ, АД, АЕ.

Такую пятерку вариаций можно сформировать для каждой из команд. То есть всего претендентов на серебро оказывается 30 (5*6).

Для каждой двойки первых призеров (чемпион-серебряный призер) можно составить только 4 комбинации с бронзовым призером. Первые два места уже распределены, так что остается 4 команды (6-2). Подберем комбинации для варианта АБ: АБВ, АБГ, АБД, АБЕ.

Мы уже подсчитали выше количество возможных комбинаций для первых двух мест – их оказалось 30. Теперь это число умножаем на 4 – получаем 120.

Выходит, что если в турнире участвует 6 команд, вариантов их размещения по первым трем местам может быть целых 120. Угадать призеров не так просто.

Сочетания и размещения: в чем же разница?

И сочетания, и размещения являются выборкой из определённого множества. Принципиальная разница между понятиями заключается лишь в том, что в случае сочетаний порядок расположения элементов не имеет значения, а в случае размещений он важен. Именно поэтому в пределах одного и того же множества количество сочетаний всегда оказывается меньше числа размещений.

Источник

Сочетания

Урок 29. Алгебра 9 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Сочетания»

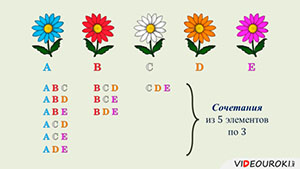
Пусть имеются 5 цветков различного цвета. Для удобств обозначим их буквами: A, B, C, D, E. Составить букеты из трёх цветков.

Если в букет входит цветок А, то можем составить такие букеты:

ABC, ABD, ABE, ACD, ACE и ADE.

Если в букет входит цветок B, но не входит А, то составим букеты:

Если же в букет входит цветок C и не входят А и B, то получим только один букет: CDE.

Мы составили все возможные сочетания из 5 элементов по 3.

Сочетанием из n элементов по k называется любое множество, составленное из k элементов, выбранных из данных n элементов. Обозначают .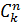

В отличие от размещений в сочетаниях не имеет значения, в каком порядке расположены элементы. Сочетания считаются различными, если они отличаются хотя бы одним элементом.

Эти два букета являются размещениями, так как в их состав входят одни и те же элементы, только с разным расположением.

А два таких букета являются сочетаниями, ведь они отличаются составом элементов.

Мы составили все сочетания из 5 элементов по 3, и выяснили, что:

Выведем формулу из n сочетаний по k. Допустим, что имеется множество из n элементов, и из них составлены все возможные сочетания по k элементов. Число таких сочетаний равно:

В каждом из этих сочетаний можно выполнить 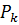перестановок. В результате мы получим все размещения, которые можно получить из n элементов по k:

Пользуясь уже известными формулами числа перестановок и размещений, получим такое равенство.

Получили формулу нахождения числа сочетаний из n элементов по k. При этом k≤n.

1. Найти число сочетаний из 7 элементов по 4.

2. Вычислим число сочетаний из 10 элементов по 5:

3. Найти число сочетаний из 15 элементов по 2:

Турист запланировал взять с собой в поездку 8 футболок, при этом всего их у него насчитывается 12. Сколькими способами он может сделать выбор?

У вас мог возникнуть вопрос, почему мы не ищем число размещений?

Но вспомнив отличие размещений от сочетаний, становиться ясно, что туристу не важно, в каком порядке он соберёт футболки. Ему важно, какие именно из них он возьмёт с собой.

Найдем число сочетаний:

В чемпионате принимало участие 8 команд. Каждая команда сыграла с каждой только 1 раз. Сколько всего было игр?

То есть нужно выяснить, сколько различных по составу пар можно получить из 8 элементов.

Найдём число сочетаний:

Получили, что всего было 28 игр.

Найти сколькими способами для участия в конкурсе можно выбрать 2 мальчика и 4 девочки, если в классе 11 мальчиков и 13 девочек?

Для начала выясним, сколькими способами можно выбрать мальчиков. Всего мальчиков 11, а выбрать нужно 2.

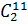
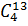
Число возможных вариантов выбора мальчиков равно , а для выбора девочек нужно .

Источник

Краткое описание

Изучение математических правил не может обойти стороной число сочетаний из n по k. Формулы комбинаторики как науки активно используются во всех жизненных отраслях. Этот раздел включён в школьную программу старших классов и вступительные испытания многих вузов России. Удивительная комбинаторика лежит в основе прикладного искусства.

Это направление науки начало активно развиваться ещё шесть веков назад. Достоверно известно, что первые комбинаторные задачи присутствовали в трудах философов и талантливых математиков Средневековья. В те времена представители стремительно развивающегося научного мира всячески пытались найти актуальные методы решения поставленных задач, хотели определить основные правила и понятия, а также утвердить уникальные в своём роде формулы и математические уравнения для тех, кто ещё не знаком с этим научным направлением.

Актуальные формулы и нормы комбинаторики применяются в распространённой теории вероятностей, где специалисты могут быстро и качественно подсчитать процент случайных событий, чтобы в итоге получить закон реального распределения случайных величин. При правильном подходе можно углублённо изучать закономерности тех или иных событий, что очень важно для понимания статистических природных правил, которые неизбежно проявляются в окружающей природе и эксплуатируемой технике.

Ключевые нюансы

Используемое в математике число сочетаний с повторениями можно подробно изучить по книгам и специальным изданиям. Комбинаторика подробно описана в том разделе науки, который занимается многофункциональными операциями с множеством задействованных элементов.

Экспертами было доказано, что это направление затрагивает довольно большой математический пласт, в котором ученикам предлагается изучить, сколько в мире существует различных комбинаций, подчиняющихся определённым условиям. Основной задачей этой науки можно считать требование размещения различных объектов по специальным правилам и последующее нахождение точного количества способов таких расположений.

На просторах интернета можно встретить много различных учебников и другого познавательного материала по информатике/математике для школьников, а также специальные сборники уравнений и сложных примеров для студентов, где в доступном и максимально подробном виде объяснена довольно увлекательная и познавательная комбинаторика. В начальных классах задачи на эту тему решают на специальных кружках, а вот в гимназиях с углублённым изучением точных наук ей посвящают основные уроки. Многоуровневые задачи по комбинаторике включены в программу олимпиады.

Существует ряд базовых понятий, которые нужно усвоить учащимся:

Необходимо отметить тот факт, что за основу может быть взят объект или целое явление, которое попадает в искомое множество. Перестановка затрагивает элементы, которые находятся в большом количестве и определённом порядке. Сочетание — своеобразные подмножества, пребывающие в произвольной форме. Размещение представляет собой упорядоченные подмножества в исходном множестве. Правильно посчитать нужный коэффициент можно при помощи многофункциональных онлайн-калькуляторов, которые обладают всеми необходимыми функциями.

Выборки и подсчёт суммы

Если предположить, что А = — множество из n элементов, то их совокупность будет называться выборкой объёма k из n. В этом случае действует ряд важных правил. Выборка может считаться правильно упорядоченной только в том случае, если итоговая последовательность следования всех задействованных элементов в ней была задана учеником заранее. Исключений не предусмотрено.

Различными выборками называются только те математические примеры, которые отличаются исключительно порядком следования элементов. Если отличия незначительные, тогда ученику предстоит работать с неупорядоченной комбинацией. В отдельных примерах могут допускаться или не должны допускаться повторения задействованных элементов.

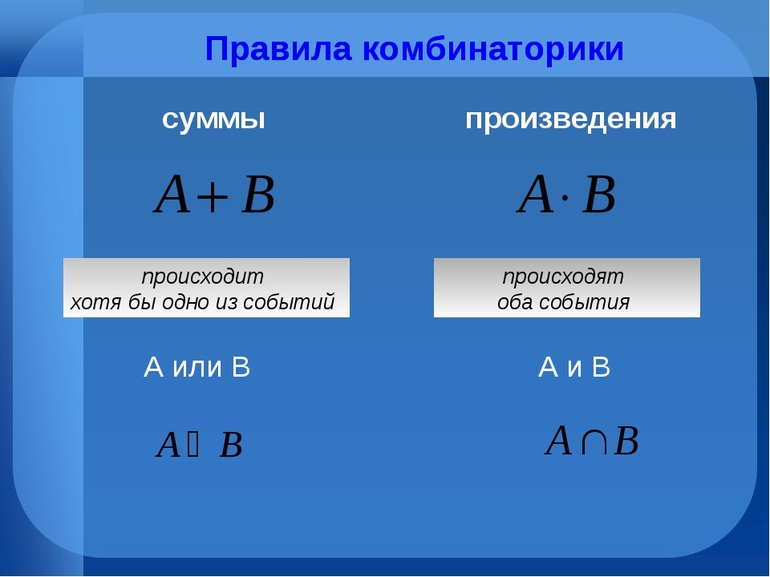
Чаще всего перед учащимися возникает необходимость подсчёта точного числа вероятных выборок с определёнными математическими параметрами. Довольно часто для контроля над вероятными комбинаторными объектами используется два ключевых приёма — правила произведения и суммы. На каждый случай специалисты предусмотрели ряд важных правил, которые призваны обезопасить учащегося от различных ошибок.

Базовое требование математического произведения основано на том, что когда исследуемый объект А может быть выбран различными f способами, то итоговый выбор А и B в указанном ранее порядке может быть осуществлён f * n методами. Правило суммы отличается тем, что если ученик имеет несколько возможностей выбрать точку А, тогда поиск А или В можно будет осуществить по специальной системе f + n.

Действующее правило произведения

Именно это направление в комбинаторике является одним из базовых для решения поставленных задач. При тщательном выборе элемента А из n способов (В из m) правильным считается то утверждение, в соответствии с которым одновременно подобрать пару А и В можно n * m методами, что очень важно. На этот случай действует три основных утверждения:

В эффективности описанных правил можно убедиться, благодаря некоторым примерам. По условиям задачи дано два ромба, три мяча, четыре гантели и пять кубов. Ученику нужно определить, сколькими способами можно будет вытянуть ромб, мяч, гантель и куб. Решение элементарное: 2*3*4*5= 120. Стоит отметить, что в этой задаче может быть задействован факториал, с помощью которого всегда можно вычислить более сложные варианты и решить трудные задачи.

По условиям следующего примера дано два мяча и пять скакалок. Задача состоит в том, чтобы определить, какова вероятность достать 1 скакалку и 1 мяч. Решение: 2*5=10.

Решение примеров комбинированного типа

Если ученик разобрался с основными свойствами сочетаний, то он также должен изучить уравнения всех доступных разновидностей задач с наиболее подходящими методами поиска правильных ответов. Эксперты рекомендуют потренироваться на более запутанных ситуациях, которые встречаются в повседневной жизни каждого человека. Основные категории задач:

Экспертами неоднократно было подтверждено, что комбинаторика является интересной и познавательной наукой, так как в наш век быстрой модернизации инновационных технологий постоянно будут нужны профессиональные специалисты, которые способны в полном объёме предоставить разнообразные решения для тех или иных практических задач.

Доступные размещения с повторениями и без них

Изучаемое число сочетаний без повторений сопряжено с некоторыми дополнительными нюансами. В этом случае в распоряжении учащегося имеется n разных математических элементов. Многих в такой ситуации интересует, сколько именно можно будет составить актуальных k расстановок.

Два базовых подхода считаются различными только при условии, если они отличаются друг от друга минимум одним элементом или состоят из аналогичных элементов, которые расположены в разном порядке. Каждый нюанс должен быть учтён, так как от этого зависит итоговый результат.

Источник