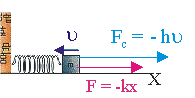что такое собственная частота колебаний

Как определить собственную частоту колебаний

Для лучшего понимания вопроса рассмотрим, что собой представляют собственные колебания и колебания в нелинейных системах.

Собственные колебания

Колебания очень схожи по природе с волнами, они подчиняются общим закономерностям, единственное их отличие в том, что в процессе распространения волн энергия не переходит из одной формы в другую, а всего лишь переносится. Исследованием закономерностей физической природы волн и колебаний занимается теория колебаний и волн. На практике в реальных условиях без воздействия внешних факторов любые колебания со временем затухают, это связано с потерей энергии.

Колебания, по характеру взаимодействия с внешней средой, разделают на:

Рассмотрим подробнее собственные колебания.

Причиной возникновения таких колебаний является отклонение от равновесия одного или нескольких параметров системы. Такие колебания возникают под воздействием внутренних сил после выведения системы из равновесия.

Рассмотрим принцип суперпозиции, который гласит о том, что допустимое движение системы равно сумме ее произвольных движений. При незначительных отклонениях характеристик системы от положения равновесия, ее движение будет соответствовать принципу суперпозиции. Подобные движения описываются дифференциальными уравнениями линейного характера. Если рассмотреть консервативную систему, т.е. такую, в которой отсутствуют потери энергии и ее параметры постоянны во времени, то любое свободное колебание такой системы представляет собой сумму простых колебаний, меняющихся во времени с определенными частотами свободных колебаний по закону синуса.

Не нашли что искали?

Просто напиши и мы поможем

Системы бывают с одной или несколькими степенями свободы. Если состояние системы в любой конкретный момент времени описывается одним параметром, то такая система имеет одну степень свободы, если двумя – то две, тремя – три, и так далее. Как пример системы с одной степенью свободы, можно рассмотреть маятник, который совершает колебательные движения в плоскости. В этом случае любое конкретное его положение характеризуется углом его отклонения от оси вертикали. Для описания колебательной системы с двумя степенями свободы нужны два переменных параметра. Примером таких колебаний является маятник, колеблющийся в сфере. В этом случае переменными параметрами будут являться углы положения маятника относительно двух перпендикулярных плоскостей. Но зачастую движения системы с двумя степенями свободы имеют сложный негармоничный характер. Они описываются линейными уравнениями суперпозиций двух простых переменных параметров, которые происходят одновременно. Так вот, каждое из этих двух простых элементарных колебаний называют собственной или свободной, так называемой гармоникой.

Для колебательных систем, состоящих из определенного количества осцилляторов (к примеру вереница шариков, соединенных между собой маленькими пружинками), число гармоник будет равняться их числу. Для более сложных систем, таких как мембрана, например, гармоники будут различные по длине волн и их будет бесконечное множество. При заданной скорости распространения таких волн, спектр собственных частот определяется простой линейной формулой. При наличии волн с разной скоростью распространения такой линейный закон уже не действует, здесь в силу вступают различные дисперсионные уравнения.

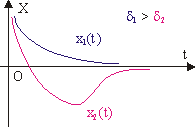
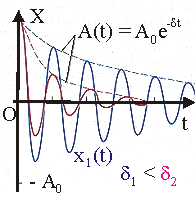
Если рассмотреть реальные существующие системы, в которых собственные колебания затухают со временем, то их считают лишь относительно гармоничными в небольшом конкретном отрезке времени. Свободные колебания, затухающие во времени, могут состоять из нескольких гармоник в определенном диапазоне частот. В таком случае имеет место так называемая добротность, то есть расширение спектральной линии, которое равно отношению запасенной энергии к потерям системы. Соответственно, сгущение спектра за счет потерь влечет за собой трансформацию его дискретной формы в сплошную в том случае, если ширина линий приближается к ширине между ними.

Сложно разобраться самому?

Попробуй обратиться за помощью к преподавателям

Колебания в нелинейных системах

Свободные или собственные колебания в нелинейных системах сложно поделить на какие-либо классы. В нелинейных системах спектр частоты свободных колебаний дискретен, что приводит к движению энергии по различным компонентам спектра. В таких колебательных системах наблюдается явление конкуренции гармоник, т.е. выживание одних за счет подавления других. Лишь дисперсия может уравновесить подобный процесс, приводя к образованию устойчивых в пространстве и времени форм колебаний.

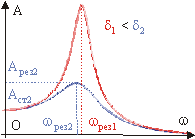
В колебательных системах частым явлением, имеющим большое значение, является процесс резонанса. Его суть заключается в резком возрастании амплитуды колебаний. Это происходит из-за приближения частоты внешнего воздействия к частоте колебания внутреннего собственного параметра системы.

Если линейная система и ее параметры находятся вне времени, то частота резонанса совпадает с частотой ее собственных колебаний. Амплитуда колебаний системы будет усиливаться с ростом параметра ее добротности. В таком случае раскачка амплитуды будет происходить до того момента, пока поступающая энергия будет больше потерь при осцилляции.

Если говорить о линейных колебаниях, то поступающая внешняя энергия пропорциональна амплитуде, а потери пропорциональны амплитуде в квадрате. Таким образом можно сказать, что баланс энергии достигается во всех известных случаях.

Источник

Как определить собственную частоту колебаний

Вы будете перенаправлены на Автор24

Собственные колебания

Собственные или свободные колебания – это колебания, происходящие в системе при отсутствии переменных внешних воздействий. Такие колебания возникают по причине начального отклонения одного из параметров от состояния равновесия.

В целом колебания представляют собой повторяющийся во времени процесс изменения состояния системы около точки равновесия (при колебании маятника все углы его отклонения от вертикали повторяются с определенной периодичностью.

В реальных макроскопических системах собственные колебания затухают по причине потерь энергии. Любой колебательный процесс связан с переходом энергии из одной формы в другую.

Следует заметить, что колебания различной физической природы имеют ряд общих закономерностей и тесно связаны с волнами. В этой связи исследованием таких закономерностей занимается теория колебаний и волн. Принципиальное отличие колебаний от волн заключается в том, что распространение последних сопровождается переносом, а не переходом энергии.

По характеру взаимодействия с окружающей средой колебания разделяют на:

В настоящей статье речь пойдет о собственных колебаниях, т.е. о колебаниях системы под действием внутренних сил после выведения системы из равновесия.

При небольших отклонениях от состояния равновесия движение любой системы будет удовлетворять принципу суперпозиции. Согласно данному принципу сумма произвольных движений составляет допустимое движение системы. Подобные движения описываются линейными (дифференциальными) уравнениями.

В случае, если в системе нет потерь энергии (она консервативна), а ее параметры не изменяются во времени, то любое собственное колебание может быть представлено, как совокупность нормальных колебаний, изменяющихся во времени по закону синуса с определенными частотами собственных колебаний.

Если положение системы в любой момент времени описывается единственным параметром, то такая система имеет одну степень свободы. Идеальным примером такой системы является маятник, колеблющийся в плоскости. И действительно, положение маятника в любой момент может определяться лишь углом его отклонения от вертикали.

Готовые работы на аналогичную тему

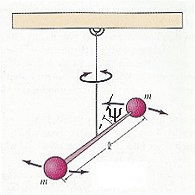
В природе существует большое количество весьма интересных систем, имеющих две степени свободы. Например, молекулы и элементарные частицы (наиболее примечательны нейтральные К-мезоны). Более простым и понятным примером является двойной маятник (один маятник подвешивается к опоре, второй – к гире первого маятника; два маятника, объединенные пружиной).

Чтобы описать состояние системы с двумя степенями свободы необходимо уже две переменные. Например, в случае со сферическим маятником роль таких переменных будут выполнять положения маятника в двух взаимно перпендикулярных плоскостях. В случае объединенных маятников эти переменные соответствуют положению каждого из маятников.

В общем виде движение системы, имеющей две степени свободы, может иметь весьма сложный вид, не напоминающий простое гармоническое движение.

Для двух степеней свободы, а также при линейных уравнениях движения общий вид движения представляет собой суперпозицию двух простейших гармонических зависимостей, происходящих в один момент. Эти два элементарных движения называют нормальными (собственными) колебаниями или гармониками.

Колебательные системы с сосредоточенными параметрами, состоящими из N связанных осцилляторов (например, цепочка из связанных между собой пружинками шариков), число гармоник будет равно N. В системах с распределенными параметрами (мембрана или резонатор) таких колебаний существует бесчисленное множество. Например, для закрепленной струны длиной L гармоники будут отличаться количеством полуволн, которые возможно уложить по всей длине струны. Если скорость распространения волн струны равна v, то спектр собственных частот определяется по формуле:

Рисунок 1. Формула 1. Автор24 — интернет-биржа студенческих работ

Наличие дисперсии волн искажает данное простое распределение частот, спектр которых определяется уже из дисперсионных уравнений.

Колебания в нелинейных системах

Собственные колебания нелинейных систем не поддаются простой классификации. Нелинейность систем с дискретным спектром частот собственных колебаний приводят к переходу энергии по спектральным компонентам. При этом возникает явление конкуренции гармоник – выживание одних и подавление других.

Подобный процесс может стабилизировать дисперсия. Она может привести к появлению устойчивых пространственно-временных образований (например, солитоны).

Большое значение при возбуждении колебаний может иметь явление резонанса, которое заключается в резком увеличении амплитуды колебаний (отклика). Данное явление наблюдается при приближении частоты внешних воздействий на систему к некоторой резонансной частоте, которая характеризует настоящую систему.

Раскачка будет происходить до тех пор, пока энергия, поступающая извне (например, полученная при отклонении маятника от положения равновесия) будет превышать потери за время осцилляции. Что касается линейных колебаний, то энергия, вносимая извне будет пропорциональна амплитуде, а потери будут расти пропорционально ее квадрату. Отсюда следует, что баланс энергии достижим во всех случаях.

Источник

собственная частота

3.2 собственная частота : Частота свободного колебания системы.

Собственную частоту плавающего пола , Гц, определяют по формуле

где — измеренная динамическая жесткость упругого материала, отнесенная к площади поверхности образца, Н/м 3 ;

3.12 собственная частота (natural frequency): Частота свободных колебаний конструкции (периодических или затухающих), зависящая только от физических характеристик этой конструкции (массы, жесткости и коэффициента демпфирования).

3.12 собственная частота (natural frequency): Частота свободных колебаний конструкции (периодических или затухающих), зависящая только от физических характеристик этой конструкции (массы, жесткости и коэффициента демпфирования).

Смотри также родственные термины:

3.2 собственная частота f₀: Частота свободного колебания системы.

Собственную частоту плавающего пола f₀, Гц, определяют по формуле

(2)

116. Собственная частота колебаний (вибрации) линейной системы

Любая из частот свободных колебаний (вибрации) линейной системы.

Примечание. Если возможны различные толкования, необходимо дать соответствующее уточнение: «собственная частота консервативной системы» или «собственная частота системы с линейным демпфированием»

55. Собственная частота колебаний линейной системы

Любая из частот свободных колебаний линейной системы

2.1.3 собственная частота колебаний. Количество гармонических колебаний в секунду.

273 собственная частота колебательного контура Частота колебательной составляющей преходящего тока

Собственная частота электродинамического сейсмоприемника

Частота свободных механических колебаний подвижной системы сейсмоприемника без затухания

Полезное

Смотреть что такое «собственная частота» в других словарях:

СОБСТВЕННАЯ ЧАСТОТА — частота нормальных колебаний или нормальныхволн динамич. системы. Физическая энциклопедия. В 5 ти томах. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988 … Физическая энциклопедия

собственная частота — Частота свободных колебаний системы. Единица измерения Гц [Система неразрушающего контроля. Виды (методы) и технология неразрушающего контроля. Термины и определения (справочное пособие). Москва 2003 г.] Тематики виды (методы) и технология неразр … Справочник технического переводчика

собственная частота f₀ — 3.2 собственная частота f0: Частота свободного колебания системы. Собственную частоту плавающего пола f0, Гц, определяют по формуле (2) где s измеренная динамическая жесткость упругого… … Словарь-справочник терминов нормативно-технической документации

собственная частота — savasis dažnis statusas T sritis automatika atitikmenys: angl. free running frequency; natural frequency vok. Eigenfrequenz, f rus. собственная частота, f pranc. fréquence propre, f … Automatikos terminų žodynas

собственная частота — savasis dažnis statusas T sritis Standartizacija ir metrologija apibrėžtis Sistemos virpesių, vykstančių dėl sukauptos energijos, kai nėra išorinio poveikio, dažnis. atitikmenys: angl. natural frequency; self frequency vok. Eigenfrequenz, f rus.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

собственная частота — savasis dažnis statusas T sritis fizika atitikmenys: angl. natural frequency; self frequency vok. Eigenfrequenz, f rus. собственная частота, f pranc. fréquence propre, f … Fizikos terminų žodynas

собственная частота — natural frequency Частота свободных гармонических колебаний недемпфируемой линейной системы. Шифр IFToMM: 3.9.39 Раздел: КОЛЕБАНИЯ В МЕХАНИЗМАХ … Теория механизмов и машин

собственная частота — Каждая из частот свободных колебаний линейной колебательной системы … Политехнический терминологический толковый словарь

собственная частота колебаний (вибрации) линейной системы — собственная частота Любая из частот свободных колебаний (вибрации) линейной системы. Примечание Если возможны различные толкования, необходимо дать соответствующее уточнение: «собственная частота консервативной системы» или… … Справочник технического переводчика

Собственная частота колебаний — (вибрации) линейной системы – любая из частот свободных колебаний (вибрации) линейной системы. Примечание. Если возможны различные толкования, необходимо дать соответствующее уточнение: «собственная частота консервативной системы» или… … Энциклопедия терминов, определений и пояснений строительных материалов

Источник

Гармонические колебания

9 класс, 11 класс, ЕГЭ/ОГЭ

Механические колебания

Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.

Колебания делятся на два вида: свободные и вынужденные.

Свободные колебания

Это колебания, которые происходят под действием внутренних сил в колебательной системе.

Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.

Вынужденные колебания

А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.

Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.

Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.

Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.

Автоколебания

Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.

У автоколебательной системы есть три важных составляющих:

Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.

Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.

Характеристики колебаний

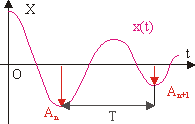
Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение характеризуется величинами: период, частота, амплитуда, фаза колебаний.

Формула периода колебаний

T = t/N

N — количество колебаний [-]

Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.

Формула частоты

ν = N/t = 1/T

N — количество колебаний [-]

Она используется в уравнении гармонических колебаний:

Гармонические колебания

Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением:

Уравнение гармонических колебаний

x — координата в момент времени t [м]

t — момент времени [с]

2πνtв этом уравнении — это фаза. Ее обозначают греческой буквой φ

Фаза колебаний

t — момент времени [с]

Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.

На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.

Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.

На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.

Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.

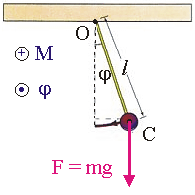
Математический маятник

Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.

Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.

Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).

Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:

Формула периода колебания математического маятника

g — ускорение свободного падения [м/с^2]

На планете Земля g = 9,8 м/с2

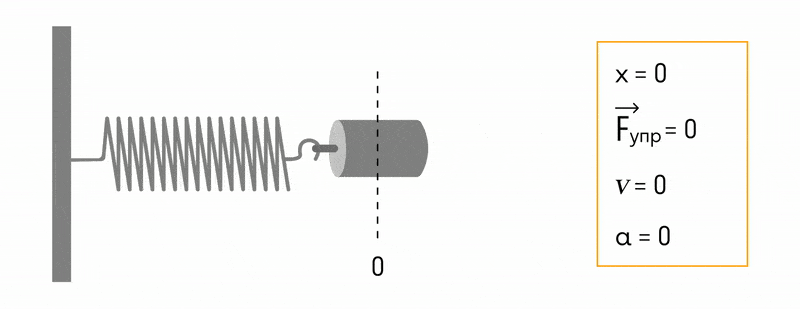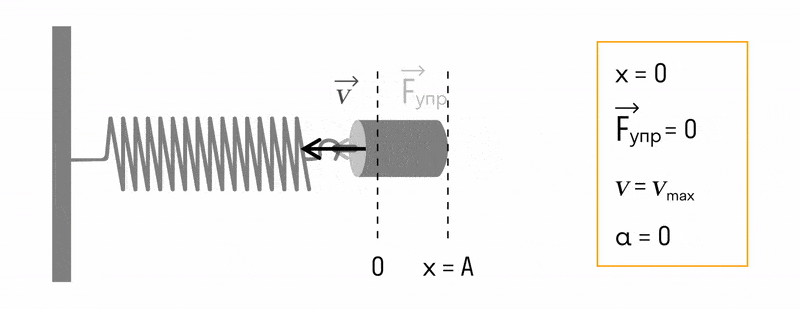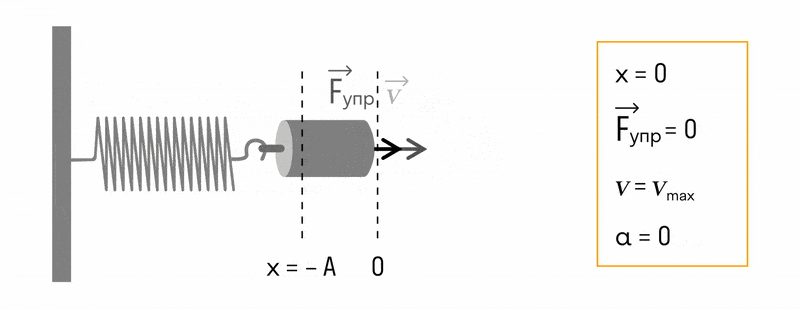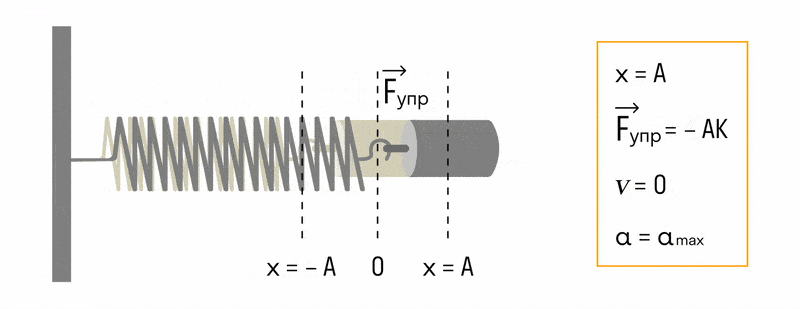
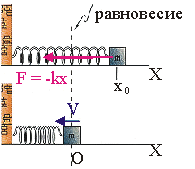
Пружинный маятник

Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.

В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.

Формула периода колебания пружинного маятника

m — масса маятника [кг]

k — жесткость пружины [Н/м]

Закон сохранения энергии для гармонических колебаний

Физика — такая клевая наука, в которой ничего не исчезает бесследно и не появляется из ниоткуда. Эту особенность описывает закон сохранения энергии.

Рассмотрим его на примере математического маятника.

Источник

Что такое собственная частота колебаний

Общие понятия теории собственных колебаний.

Собственными называются колебания, которые совершает система около положения устойчивого равновесия после первоначального возмущения под действием только внутренних сил.

Какая сила должна действовать на систему, чтобы колебания были гармоническими? Так как для гармонических колебаний уравнение, связывающее ускорение и координату материальной точки выглядят как

то согласно II закону Ньютона справедливо следующее равенство:

Итак, тело совершает гармонические колебания, если сила, возвращающая его в положение равновесия, пропорциональна смещению и направлена в противоположную этому смещению сторону.
Такая сила называется квазиупругой.

На практике зависимость F(x) является более сложной. Однако, при малых значениях величины х эту функцию можно разложить в ряд:

и пренебречь слагаемыми более высокого, чем 1 порядка малости. Следовательно, любая система с одной степенью свободы при достаточно малом отклонении от положения равновесия будет гармонически колебаться.

Рис. 10.1.

Значение w₀ зависит только от физических свойств системы и не зависит от начальных условий.

Рис. 10.2. Крутильные колебания.

Сравнивая уравнения (10.6) и (10.1), видим, что они аналогичны. Следовательно, решение уравнения (10.6) имеет вид гармонической функции:

Рис. 10.3. Колебания физического маятника.

Решение этого уравнения имеет следующий вид:

Для математического маятника момент инерции и значение собственной частоты колебаний будут равны:

Собственную частоту физического маятника можно представить в виде, аналогичном выражению для математического маятника:

Собственные затухающие колебания. Логарифмический декремент затухания.

Рис. 10.4.

Уравнение динамики затухающих колебаний. В реальных случаях на тело, совершающее собственные гармонические колебания, действует сила трения. Наиболее распространен случай жидкого трения, когда сила трения (сопротивления среды) пропорциональна скорости:

Уравнение (10.7) справедливо для малых скоростей. Согласно II закону Ньютона уравнение движения тела будет иметь вид:

После несложных преобразований получим:

Рис. 10.6. Затухающие колебания в случае большого трения.

и определяется характеристиками колеблющейся системы и окружающей среды. Таким образом, трение уменьшает частоту колебаний. Качественно этот факт можно объяснить так. Сила трения действует против скорости. Следовательно, для линейного осциллятора ее действие эквивалентно уменьшению возвращающей силы, т.е. упругости пружины. Это означает, что частота колебаний w уменьшается, а период Т увеличивается.

Рис. 10.5. Затухающие колебания.

При большом трении тело колебаний как таковых не совершает (см. рис. 10.6, кривая x₁(t) ). Решение будет иметь вид:

Возможен и промежуточный вариант, также характерный для больших значений коэффициента затухания (кривая x₂(t) на рис. 10.6).

величина 1/ d , равна промежутку времени, по истечении которого амплитуда колебаний уменьшается в е = 2.73 раз.

Рис. 10.7. К определению логарифмического декремента затухания.

называется логарифмическим декрементом затухания. Выясним связь между d и d :

Используя уравнение (10.13), можно преобразовать закон изменения амплитуды:

Величина 1/d равна числу колебаний, за которое их амплитуда уменьшается в е раз.

Если значение d невелико ( d ), то можно показать, что

Динамика вынужденных колебаний. Резонанс.

Уравнение динамики колебаний, происходящих под действием гармонической силы. Вынужденными называются колебания, которые система совершает под действием внешней силы. Характер движения зависит от особенностей внешней силы. Она может быть любой периодически изменяющей свое значение. Наиболее важным является случай гармонической внешней силы. Более сложные случаи ее изменения во времени сводятся к этому простейшему.

Будем считать, что внешняя сила действует на линейный гармонический осциллятор по следующему закону:

Кроме внешней силы на осциллятор, по-прежнему, действуют квазиупругая сила и сила трения. Согласно II закону Ньютона уравнение движения имеет вид:

Рис. 10.8.

Таким образом, общее решение будут иметь вид:

Первое слагаемое правой части этого выражения описывает собственные затухающие колебания, зависящие от начальных условий. Из уравнения (10.18) следует, что в течение определенного промежутка времени осциллятор будет совершать сложное негармоническое движение, т.к. оно является результатом сложения двух асинхронных колебаний. Однако, через промежуток времени t

1/ d амплитуда и энергия собственных колебаний уменьшатся до нуля и они прекратятся. При этом второе слагаемое останется неизменным и результирующее колебание будет гармоническим (см. рис. 10.8, 10.9).

Рис. 10.9.

Переходной и установившийся режимы колебаний. Колебания, которые будут совершаться после затухания собственных колебаний, называются установившимися вынужденными колебаниями. Процесс установления этих колебаний называется переходным режимом (см. рис. 10.8).

Установившиеся колебания не зависят от начальных условий и описываются уравнением:

Амплитуда вынужденных колебаний пропорциональна амплитуде вынуждающей силы и существенно зависит от соотношения между частотой вынуждающей силы и собственной частотой.

Величину сдвига фаз между смещением и вынуждающей силой будет равна:

Обратите внимание, что смещение отстает по фазе от вынуждающей силы.

Рис. 10.10. Амплитудно-резонансная кривая.

Из графика видно, что при определенном значении частоты вынуждающей силы амплитуда осциллятора становится максимальной.

Явление, при котором амплитуда колебаний системы достигает максимального значения, характерного для некоторого значении частоты вынуждающей силы называется резонансом.

Частота вынуждающей силы, при которой наступает данное явление, называется резонансной. Приравнивая к нулю производную по частоте выражения (10.20) и пренебрегая слагаемыми второго порядка малости, получим формулы для расчета резонансной частоты w _рез и амплитуды А_рез :

При значении d = 0 амплитуда колебаний в резонансе стремится к бесконечности.

Важной характеристикой осциллятора является отношение амплитуды его колебаний в резонансе к ее статическому значению. Из формул (10.21) и (10.23) следует, что это отношение равно добротности системы:

Добротность является важнейшей характеристикой резонансных свойств системы.

Рассмотрим чему равен сдвиг фаз между смещением и силой при резонансе. Допустим, что при w = w ₀ сила и смещение подчиняются следующим законам:

Тогда уравнение для скорости колеблющейся частицы (осциллятора) имеет вид:

Из этих соотношений видно, что скорость u и сила колеблются в фазе. Следовательно, мощность, сообщаемая осциллятору внешней силой, равна N = F· u. Ее значение положительно в любой момент времени, следовательно, работа внешней силы достигает своего максимального значения. Энергия, передаваемая осциллятору внешней силой, в этом случае направлена на преодоление сил трения.

Примеры . Явление резонанса используется в работе резонансных контуров в электрических схемах, усиливающих полезный сигнал, наличие резонанса необходимо учитывать при расчете механических конструкций на прочность.

Источник

• ← что такое социальное государство определение
• что делать с ожоговыми волдырями →