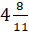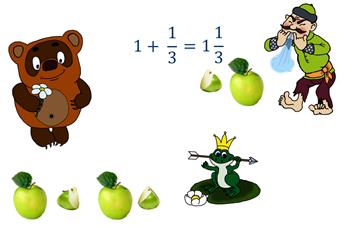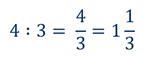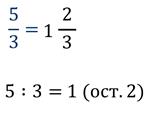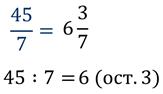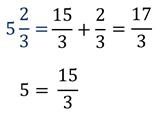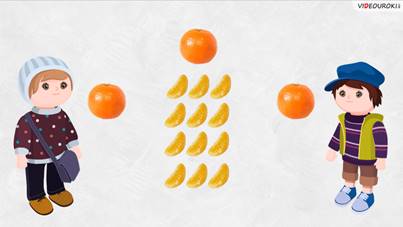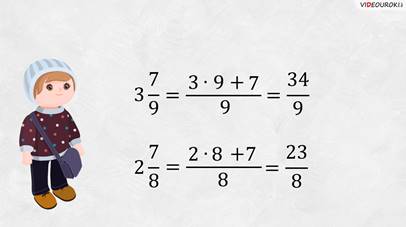что такое смешанное число в математике 5 класс

Смешанные числа

Содержание

Знакомство со смешанными числами

А что будет, если мы будем делить на четверых 5 яблок?

Можно так же разрезать каждое яблоко на 4 кусочка, и каждый возьмёт 5 четвертинок. Но обычно делают не так.

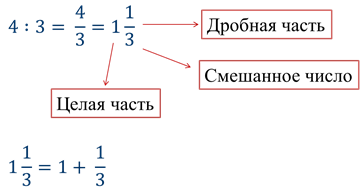
Читается это как «Одна целая одна четвёртая». Подобную запись (целое число и дробь) называют «смешанной», а само число – «смешанным числом». Запись числа, содержащую целую и дробную части, называют смешанной.

Выделение смешанного числа из неправильной дроби

Как думаете, из любой дроби можно сделать смешанное число?

Нет, только из неправильной дроби. В правильной дроби просто «не хватает» долей числа на то, чтобы из них получилась целая часть.

Нужно разделить 11 на 5, 11 на 5 не делится, берём ближайшее число – 10.

Чтобы из неправильной дроби выделить целую часть, надо:
1) разделить числитель на знаменатель
2) если деление произошло без остатка, результатом будет целое число, если же деление прошло с остатком, то неполное частное будет целой частью. Остаток становится числителем, а делитель – знаменателем дробной части.

Превращение смешанной дроби в неправильную дробь

А если нам нужно, наоборот, превратить смешанную дробь в неправильную?

Сначала нам нужно представить целую часть в виде дроби с таким же знаменателем, как у дробной части, а потом сложить получившуюся дробь с дробной частью.

Разберём на примере.

Чтобы представить смешанное число в виде дробной части, надо:
1) умножить целую часть дроби на знаменатель дробной части
2) прибавить получившееся произведение к числителю дробной части. Знаменатель оставить без изменения.

Буквами это можно записать так:

Лена, Марина и Никита делили несколько шоколадок поровну: каждому дали по шоколадке, а оставшуюся лишнюю разделили на 3 части. Но Никита сказал, что шоколадки-то одинаковые по размеру, но что, если они все с разными вкусами? Честнее и интереснее будет разломить каждую шоколадку на 3 части, а потом каждый возьмёт себе равное количество частей.

Можете сказать, сколько частей шоколадки было у каждого? А сколько всего частей шоколадок у них получилось? И сколько целых шоколадок было в начале?

Получается, что каждый взял по 4 части.

А когда шоколадки разломили на кусочки, сколько получилось?

То есть у них получилось 12 третьих частей шоколадки.

Источник

Смешанные числа

Урок 29. Математика 5 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Смешанные числа»

На этом уроке мы узнаем, какие числа называют смешанными. Научимся выделять целую часть. А также применим свои знания на конкретных примерах.

Мы с вами на прошлых уроках разобрались, как делить меньшее число на большее. А вот, если нужно разделить большее число на меньшее, и при этом числа не делятся нацело? Как же поступить в таком случае?

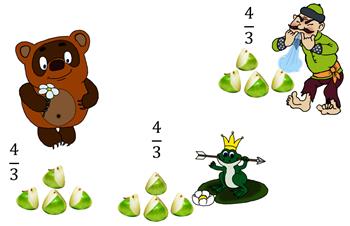
Винни Пух принёс на полянку 4 яблока и решил поделиться ими со своими друзьями: Царевной лягушкой, и Соловьём Разбойником. Как Винни Пуху разделить яблоки, чтобы все остались довольны?

Видим, что результат деления не зависит от способа решения задачи, который мы выбрали. Значит можно записать, что

Число 1 называют целой частью числа 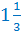, а число – его дробной частью.

Запись вида 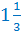называют смешанным числом, и равняется сумме его целой части и дробной.

Научимся переводить неправильную дробь в смешанное число.

Запомним правило выделения целой части из неправильной дроби:

1) Разделить с остатком числитель на знаменатель.

2) Неполное частное будет целой частью.

3) Остаток (если он есть) даёт числитель, а делитель – знаменатель дробной части.

Выделить целую часть из неправильной дроби: .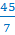

Любое смешанное число можно представить в виде неправильной дроби.

Представить дробь 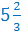в виде неправильной дроби.

Запомним правило представления смешанного числа в виде неправильной дроби:

1) Нужно целую часть числа умножить на знаменатель дробной части.

2) К полученному произведению прибавить числитель дробной части.

3) Записать полученную сумму числителем дроби, а знаменатель дробной части оставить без изменения.

Итак, сегодня на уроке мы узнали, какие числа называют смешанными. Научились, выделять целую часть из неправильной дроби, представлять смешанное число в виде неправильной дроби, а также применили свои знания на конкретных примерах.

Источник

Смешанные числа

Урок 29. Математика 5 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Смешанные числа»

– Паша, привет. Хочешь мандарин?

– Привет, Саша. Да, хочу. Я очень люблю мандарины.

– Смотри, у меня 3 мандарина, нас двое. Надо как-то эти мандарины разделить.

– Давай почистим все мандарины, посчитаем, сколько всего долек, и поделим их на 2.

– Давай. Смотри, в каждом мандарине 12 долек. У нас 3 мандарина, значит, и долек 36. Каждому получается по 18 долек.

– Подожди, Саша. Но мы можем же мандарины поделить и по-другому. Взять каждый по одному, а третий мандарин разделить пополам. В нём 12 долек, значит, каждый получит по 1 целому мандарину и по 6 долек.

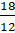
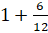
– Ты прав, Паша. И как тогда записать? Если мы берём по 18 долек, то можем это записать как . Потому что в каждом мандарине по 12 долек. А если делим так, как ты предложил, то записать как? , что ли?

– Ничего не понимаю. Давай пойдём к Электроше. Он точно нам поможет разобраться.

– Электроша, привет. Смотри, мы попробовали разделить на двоих 3 мандарина и у нас что-то не очень понятное получилось. Если сначала мандарины разделить на дольки и делить их, то получится, что каждый из нас должен взять 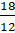мандарина, а если сначала каждому взять по одному целому мандарину, а оставшийся поделить на дольки, то получится, что у каждого из нас 1 целый мандарин и ещё 6 двенадцатых мандарина. Как записать такое деление?

– Успокойтесь, ребята. Сейчас мы с вами во всём разберёмся, но сначала давайте устно выполним несколько упражнений.

Вернёмся к вашей задаче.

Запишем дробь 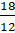. Какая это дробь? Паша, ты помнишь, как называются такие дроби?

– Конечно, Электроша, помню. Числитель этой дроби больше знаменателя, значит, перед нами неправильная дробь.

Давайте подумаем, суммой каких дробей её можно представить?

– Ну, например, .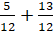

– Или .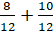

Мы можем ещё долго перечислять.

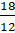
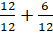
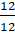
– Да, мальчики, вы правильные суммы называете. А давайте запишем в виде суммы дробей . Что вы можете сказать о дроби ?

– Числитель равен знаменателю, значит, эта дробь равна 1. То есть нашу дробь можно записать так: .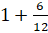

– А 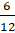– это какая дробь?

– Числитель меньше знаменателя, значит, это правильная дробь.

– Ой, – удивился Саша, – так у нас же получилось то же самое, когда мы сначала взяли себе по целому мандарину, а потом оставшийся мандарин поделили пополам.

– Конечно, Саша. У вас и должно было так получиться.

У нас получилось, что неправильную дробь мы представили в виде суммы натурального числа и правильной дроби.

Давайте посмотрим, может, это только дробь 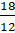можно так представить?

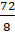
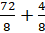
Возьмём дробь . И представим её в виде суммы двух дробей .

Чему равна дробь 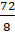? Паша, ты можешь подсчитать?

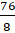
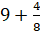
– Конечно. Эта дробь равна 9. Тогда получим, что дробь равна сумме .

Опять получилась сумма натурального числа и правильной дроби. Так что получается, Электроша? Любую неправильную дробь можно представить в виде такой суммы?

– Да, запомните правило: любую неправильную дробь, у которой числитель не делится нацело на знаменатель, можно представить в виде суммы натурального числа и правильной дроби.

Обратите внимание на слова «числитель не делится нацело на знаменатель». Если же числитель делится нацело на знаменатель, например, дробь , то такая дробь равна просто натуральному числу, в нашем случае, 3.

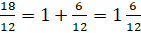
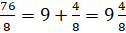
Но вернёмся к нашим примерам. Как правило, такие суммы записывают так , и читают: «одна целая шесть двенадцатых» и «девять целых четыре восьмых».

Числа такого вида называют смешанными числами. Ну, почему такое название, я думаю, вам понятно.

– Да, Электроша, ясно. Смешали натуральные числа и дробные, вот и получились смешанные числа.

– Да, Саша, ты прав. У каждого компонента смешанной дроби есть своё название.

Так, натуральное число называют целой частью смешанного числа, а дробь – дробной частью смешанного числа.

Обратите внимание, дробная часть смешанного числа – это обязательно правильная дробь.

Например, число 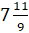– это несмешанное число, потому что – это неправильная дробь.

– Всё понятно, Электроша. А дай нам задание, чтобы проверить, как мы поняли, что такое смешанные числа.

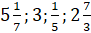
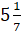
Среди предложенных чисел укажите смешанные. Начинай ты, Паша.

– – это смешанное число. У него есть целая часть и дробная часть. В дробной части – правильная дробь.

Число 3 несмешанное, так как у него нет дробной части.

тоже несмешанное число, потому что у него нет целой части.

– это несмешанное число, потому что в дробной части этого числа находится неправильная дробь.

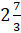
Сейчас мы с вами научимся переводить неправильную дробь в смешанное число.

То есть разберём то, как правильно выделять или, другими словами, находить целую и дробную части числа.

Давайте посмотрим на дробь 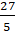. Это неправильная дробь, и 27 без остатка на 5 не делится. То есть мы точно можем представить эту дробь суммой натурального числа и правильной дроби, другими словами, смешанным числом.

Выполним деление с остатком числа 27 на 5.

Получим, что 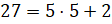. Здесь 5 – это неполное частное, а 2 – остаток. Тогда целой частью смешанного числа будет число 5, а числителем дробной части – число 2. Знаменателем дробной части смешанного числа будет знаменатель неправильной дроби, то есть 5.

– Ну как, мальчики, вы всё поняли?

– Вроде бы, да. Но давай решим какое-нибудь задание, чтобы нам стало ещё яснее.

Вот задание для тебя, Саша.

Переведите неправильные дроби в смешанные числа .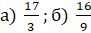

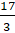
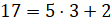
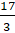
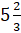
Первая дробь – . Разделим 17 на 3. Получим, что . Тогда можем записать, что равно смешанному числу .

– Я так понял, Электроша?

– Да, Саша. Ты всё правильно понял. Продолжай.

. Разделим 16 на 9 с остатком. Получим, что . Тогда дробь равна .

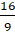
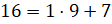
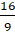
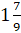
Запомните правило: для того, чтобы неправильную дробь, у которой числитель не делится нацело на знаменатель, преобразовать в смешанное число, надо числитель разделить на знаменатель.

Полученное неполное частное записывается как целая часть смешанного числа, а остаток – как числитель дробной части смешанного числа.

Знаменатель дробной части будет равен знаменателю неправильной дроби.

Теперь давайте вернёмся к предыдущему правилу и немного его исправим. Теперь можно записать так: любую неправильную дробь, у которой числитель нацело не делится на знаменатель, можно представить в виде смешанного числа.

Ну что, вам стало понятно, что такое смешанные числа и как неправильные дроби в них переводить?

– Да, это понятно. Но вот интересно, а смешанное число можно перевести в неправильную дробь?

Давайте возьмём, например, число .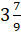

Представим это число в виде суммы .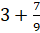

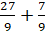
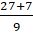
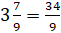
Мы помним, что любое натуральное число можно представить в виде дроби с любым знаменателем. Представим 3 в виде дроби со знаменателем 9. Получим, что смешанное число равно . Как складываются дроби с одинаковыми знаменателями, мы знаем . Получим, что .

Попробуй, Саша, перевести число 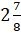в неправильную дробь.

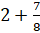
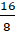
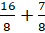
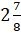
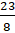
– Представим это число в виде суммы . 2 запишем как . Сложим и получим, что можно представить в виде неправильной дроби .

Есть правило, которое помогает упростить перевод смешанного числа в неправильную дробь.

Для того, чтобы преобразовать смешанное число в неправильную дробь, надо целую часть числа умножить на знаменатель дробной части. К полученному произведению надо добавить числитель дробной части. Эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа.

Вернёмся к нашим примерам и попробуем перевести смешанное число в дробь по этому правилу , .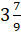

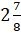
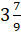
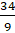
Начнём с . Умножим 3 на 9 и прибавим 7. Это будет числитель неправильной дроби, а знаменателем дроби будет число 9. Получим дробь .

Попробуй, Паша, перевести этим способом в дробь число .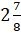

– Умножим 2 на 8 и добавим 7. Получим, что числитель неправильной дроби будет равен 23. А знаменатель – 8. .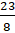

Выполните такое задание.

Преобразуйте смешанные числа в дроби, а неправильные дроби – в смешанные числа .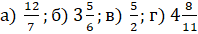

– Итак, дробь .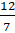

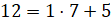
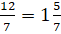
Разделим 12 на 7 с остатком. Получим . Тогда .

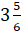
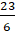
Переведём в неправильную дробь. Умножим 3 на 6 и добавим 5. Получим, что числитель дроби равен 23. Знаменатель дроби будет равен 6. .

– Теперь, Паша, продолжи решать ты.

Дробь . Разделим 5 на 2 с остатком. Получим . То есть дробь .

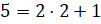
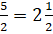
Для того, чтобы перевести число в неправильную дробь, умножим 4 на 11 и прибавим 8. Числитель дроби будет равен 52. Знаменатель дроби будет равен 11.

Источник