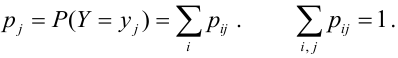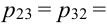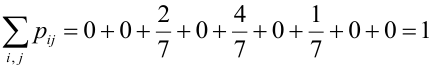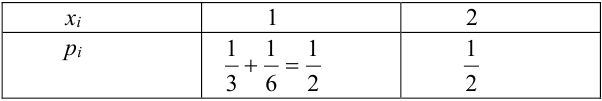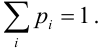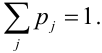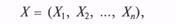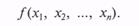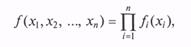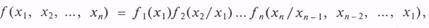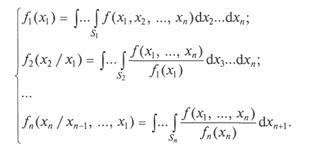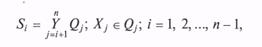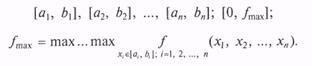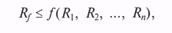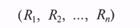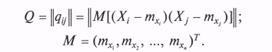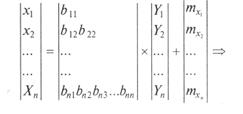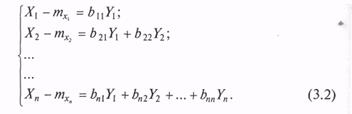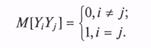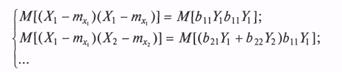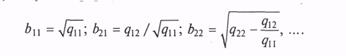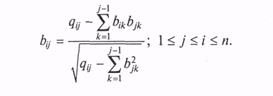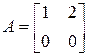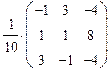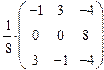что такое случайный вектор

Содержание:

Системы случайных величин или случайные векторы:

При изучении случайных явлений в зависимости от их сложности приходится использовать два, три и большее число случайных величин.

Например, 1) попадание снаряда в цель определяется не одной, а двумя случайными величинами: абсциссой и ординатой точки попадания, 2) случайное отклонение точки разрыва снаряда при дистанционной стрельбе определяется комплексом трех случайных величин: тремя координатами этой точки.

Определение 57. Совместное рассмотрение двух или нескольких случайных величин приводит к системе случайных величин или к случайному вектору.

Геометрическая интерпретация системы: 1) систему двух случайных величин (X, У) рассматривают как случайную точку на плоскости (Охх) или как случайный вектор с составляющими X, У; 2) систему трех случайных величин (X, У, Z) рассматривают как случайную точку на плоскости (Оxyz) или как случайный вектор с составляющими X, У; Z и т.д.

В зависимости от типа случайных величин, образующих систему, могут быть дискретные, непрерывные и смешанные системы.

Определение 58. Двумерный случайный вектор (X, У) называется вектором дискретного типа (СВДТ), если множество его возможных значений не более, чем счетно.

Определение 59. (первое определение) Двумерный случайный вектор (X, У) называется вектором непрерывного типа (СВНТ), если множество его возможных значений непрерывно заполняет некоторую область плоскости (Оху)-

Определение 60. Законом распределения системы случайных величин называется соотношение, устанавливающее связь между областями возможных значений системы случайных величин и вероятностями появления системы в этих областях.

Законы распределения СВДТ и СВНТ

Пример:

Решение.

(0 четных, 0 нечетных) = 0, не выбираем ни одной цифры, а по условию выбираем две цифры. Аналогично, (выбираем всего одну цифру либо нечетную, либо четную), (выбираем три цифры вместо двух по условию), (выбираем четыре цифры вместо двух по условию).

— (обе цифры нечетные),

— (одна четная, одна нечетная),

— (обе цифры четные).

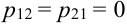
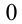
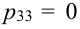
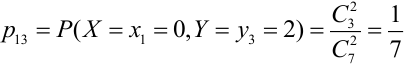
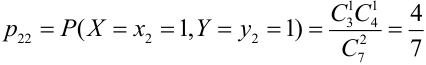
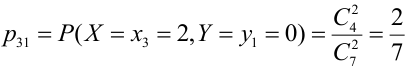
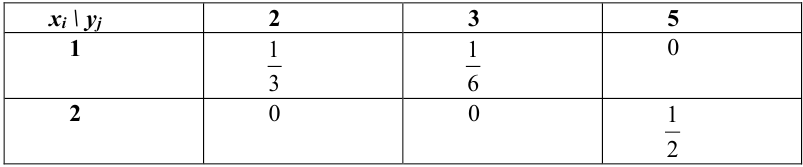
Таблица распределения имеет вид:

Проверка:

Пример:

Дана таблица распределения случайного вектора (X, Y). Получить ряды распределения для Х и Y отдельно.

Решение.

, (складываем по строкам), следовательно,

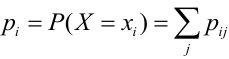
Проверка:

, (складываем по столбцам), следовательно,

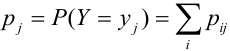
Проверка:

Определение 61. Функцией распределения системы двух случайных величин называется функция двух аргументов F(x,y), равная вероятности совместного выполнения двух неравенств: X

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Случайный вектор

Смотреть что такое «Случайный вектор» в других словарях:

n-мерный случайный вектор — 11. n мерный случайный вектор Конечное семейство случайных величин ξn = (ξ1, ξ2. ξn) Источник: ГОСТ 21878 76: Случайные процессы и динамические системы. Термины и определения … Словарь-справочник терминов нормативно-технической документации

Вектор — Вектор многозначный термин; величина, характеризующаяся размером и направлением. В Викисловаре есть статья «вектор» … Википедия

Вектор (значения) — Вектор: Содержание 1 В биологии 2 В информатике 3 В математике 4 В физике … Википедия

Случайный элемент — обобщение понятия случайной величины. Термин был введён, по видимому, М.Фреше (1948), отмечавшим, что «развитие теории вероятностей и расширение области её приложений привели к необходимости перейти от схем, где (случайные) исходы опыта могут… … Википедия

ВЕКТОР — математич. абстракция объектов, характеризующихся величиной и направлением. Понятие В. может быть введено аксиоматически (что делается в математике при определении векторного пространства). В социологии чаще всего используются В., каждый из к рых … Российская социологическая энциклопедия

СЛУЧАЙНЫЙ ПРОЦЕСС — стохастический процесс, вероятностный процесс, случайная функция времени, процесс (т. е. изменение во времени состояния нек рой системы), течение к рого зависит от случая и для к рого определена вероятность того или иного его течения. Типичным… … Математическая энциклопедия

Компонента вектора — Вектор: Содержание 1 В биологии 2 В информатике 3 В математике 4 В физике … Википедия

ГОСТ 21878-76: Случайные процессы и динамические системы. Термины и определения — Терминология ГОСТ 21878 76: Случайные процессы и динамические системы. Термины и определения оригинал документа: Cross power spectral density function of stationary dependent random processes Определения термина из разных документов: Cross power… … Словарь-справочник терминов нормативно-технической документации

ГОСТ Р 52633.0-2006: Защита информации. Техника защиты информации. Требования к средствам высоконадежной биометрической аутентификации — Терминология ГОСТ Р 52633.0 2006: Защита информации. Техника защиты информации. Требования к средствам высоконадежной биометрической аутентификации оригинал документа: 3.1 автоматическое обучение: Обучение, осуществляемое автоматически без… … Словарь-справочник терминов нормативно-технической документации

Многомерное нормальное распределение — (или многомерное гауссовское распределение) в теории вероятностей это обобщение одномерного нормального распределения. Определения Случайный вектор имеет многомерное нормальное распределение, если выполняется одно из следующих эквивалентных … Википедия

Источник

Случайный вектор

Смотреть что такое «Случайный вектор» в других словарях:

n-мерный случайный вектор — 11. n мерный случайный вектор Конечное семейство случайных величин ξn = (ξ1, ξ2. ξn) Источник: ГОСТ 21878 76: Случайные процессы и динамические системы. Термины и определения … Словарь-справочник терминов нормативно-технической документации

Вектор — Вектор многозначный термин; величина, характеризующаяся размером и направлением. В Викисловаре есть статья «вектор» … Википедия

Вектор (значения) — Вектор: Содержание 1 В биологии 2 В информатике 3 В математике 4 В физике … Википедия

Случайный элемент — обобщение понятия случайной величины. Термин был введён, по видимому, М.Фреше (1948), отмечавшим, что «развитие теории вероятностей и расширение области её приложений привели к необходимости перейти от схем, где (случайные) исходы опыта могут… … Википедия

ВЕКТОР — математич. абстракция объектов, характеризующихся величиной и направлением. Понятие В. может быть введено аксиоматически (что делается в математике при определении векторного пространства). В социологии чаще всего используются В., каждый из к рых … Российская социологическая энциклопедия

СЛУЧАЙНЫЙ ПРОЦЕСС — стохастический процесс, вероятностный процесс, случайная функция времени, процесс (т. е. изменение во времени состояния нек рой системы), течение к рого зависит от случая и для к рого определена вероятность того или иного его течения. Типичным… … Математическая энциклопедия

Компонента вектора — Вектор: Содержание 1 В биологии 2 В информатике 3 В математике 4 В физике … Википедия

ГОСТ 21878-76: Случайные процессы и динамические системы. Термины и определения — Терминология ГОСТ 21878 76: Случайные процессы и динамические системы. Термины и определения оригинал документа: Cross power spectral density function of stationary dependent random processes Определения термина из разных документов: Cross power… … Словарь-справочник терминов нормативно-технической документации

ГОСТ Р 52633.0-2006: Защита информации. Техника защиты информации. Требования к средствам высоконадежной биометрической аутентификации — Терминология ГОСТ Р 52633.0 2006: Защита информации. Техника защиты информации. Требования к средствам высоконадежной биометрической аутентификации оригинал документа: 3.1 автоматическое обучение: Обучение, осуществляемое автоматически без… … Словарь-справочник терминов нормативно-технической документации

Многомерное нормальное распределение — (или многомерное гауссовское распределение) в теории вероятностей это обобщение одномерного нормального распределения. Определения Случайный вектор имеет многомерное нормальное распределение, если выполняется одно из следующих эквивалентных … Википедия

Источник

Моделирование случайных векторов

Случайным вектором (системой случайных величин) называют совокупность случайных величин, совместно характеризующих какое-либо случайное явление

где X_i — СВ с теми или иными законами распределения.

Данный подпункт содержит материал по методам моделирования непрерывных случайных векторов (все компоненты которых представляют собой непрерывные СВ).

Проще всего моделировать случайный вектор с независимыми компонентами, для которого справедливо

т.е. каждую из компонент случайного вектора можно моделировать независимо от других в соответствии с ее «собственной» плотностью вероятности f_i(x_i).

В случае, когда компоненты случайного вектора статистически зависимы, необходимо использовать специальные методы: условных распределений, исключения (фон Неймана), линейных преобразований.

Метод условных распределений.Метод основан на рекуррентном вычислении условных плотностей вероятностей для каждой из компонент случайного вектора х с многомерной совместной плотностью вероятности f(x₁, х₂, …, x_n).

Для плотности распределения случайного вектора х можно записать:

Для получения указанных плотностей необходимо провести интегрирование совместной плотности распределения случайного вектора в соответствующих пределах:

Алгоритм метода следующий.

1. Генерируются (n + 1) ПСЧ

распределенных соответственно на интервалах

2. Если выполняется условие

и есть искомая реализация случайного вектора.

3. Если данное условие не выполняется, переходят к первому пункту и т.д.

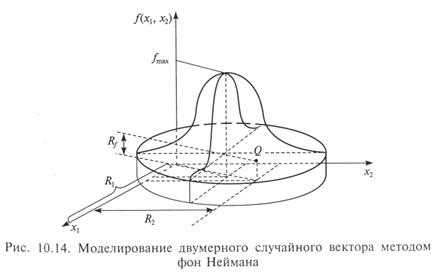
Рис. 10.14 содержит иллюстрацию данного алгоритма для двумерного случая R_f £ f(R₁, R₂).

Возврат к п. 1 после «неудачного» моделирования п ПСЧ происходит тогда, когда точка Q окажется выше поверхности, представляющей двумерную плотность вероятности f(x₁, x₂). Для случая, представленного на рисунке, в качестве (очередной) реализации двумерного случайного вектора следует взять пару ПСЧ (R₁, R₂).

Среднюю относительную частоту «неудач» можно вычислить геометрическим способом, взяв отношение объемов соответствующих фигур.

Как уже отмечалось для одномерного случая, основным достоинством метода фон Неймана является его универсальность. Однако для плотностей вероятностей, поверхности которых имеют острые пики, достаточно часто будут встречаться «пустые» прогоны, когда очередные п ПСЧ бракуются. Этот недостаток тем существеннее, чем больше размерность моделируемого вектора (п) и длиннее требуемая выборка реализаций случайного вектора. На практике такие ситуации встречаются не слишком часто, поэтому метод исключений и имеет столь широкое распространение.

Метод линейных преобразований.Метод линейных преобразований является одним из наиболее распространенных так называемых корреляционных методов, применяемых в случаях, когда при моделировании непрерывного n-мерного случайного вектора достаточно обеспечить лишь требуемые значения элементов корреляционной матрицы этого вектора (это особенно важно для случая нормального распределения, для которого выполнение названного требования означает выполнение достаточного условия полного статистического соответствия теоретического и моделируемого распределений). Идея метода заключается в линейном преобразовании случайного n-мерного вектора Y cнезависимыми (чаще всего нормально распределенными) компонентами в случайный вектор X с требуемыми корреляционной матрицей и вектором математических ожиданий компонент.

Математическая постановка задачи выглядит следующим образом. Даны корреляционная матрица и математическое ожидание вектора X

Требуется найти такую матрицу В, которая позволяла бы в результате преобразования

где Y — n-мерный вектор с независимыми нормально распределенными компонентами со стандартными параметрами, получить вектор Х стребуемыми характеристиками.

Будем искать матрицу В в виде нижней треугольной матрицы, все элементы которой, расположенные выше главной диагонали, равны 0. Перейдем от матричной записи к системе алгебраических уравнений:

Поскольку компоненты вектора у независимы и имеют стандартные параметры, справедливо выражение

Почленно перемножив сами на себя и между собой соответственно левые и правые части уравнений системы (3.2) и взяв от результатов перемножения математическое ожидание, получим систему уравнений вида

Как легко увидеть, в левых частях полученной системы уравнений — элементы заданной корреляционной матрицы Q, ав правых — элементы искомой матрицы В. Последовательно решая эту систему, получаем формулы для расчета элементов b_ij:

Формула для расчета любого элемента матрицы преобразования В имеет вид

Таким образом, алгоритм метода линейных преобразований весьма прост:

· по заданной корреляционной матрице рассчитывают значения коэффициентов матрицы преобразования В;

· генерируют одну реализацию вектора Y, компоненты которого независимы и распределены нормально со стандартными параметрами;

· полученный вектор подставляют в выражение (3.1) и определяют очередную реализацию вектора X, имеющего заданные корреляционную матрицу и вектор математических ожиданий компонентов;

· при необходимости два предыдущих шага алгоритма повторяют требуемое число раз (до получения нужного количества реализаций вектора X).

В данной главе рассмотрены основные методы генерации ПСЧ, равномерно распределенных на интервале [0; 1], и моделирования случайных событий, величин и векторов, часто используемые в практике имитационных исследований ЭИС. Как правило, все современные программные средства, применяемые для реализации тех или иных имитационных моделей, содержат встроенные генераторы равномерно распределенных ПСЧ, что позволяет исследователю легко моделировать любые случайные факторы.

Источник

Случайные векторы и их характеристики

Тема 1. Математическое и программное обеспечение процесса

Моделирования

Линейная алгебра

Повторите основные понятия линейной алгебры: линейное пространство, векторы, линейная комбинация векторов, линейная зависимость векторов, матрицы, ранг матрицы, действия с матрицами, обратная и транспонированная матрица, вычисление определителя.

1. Свойства матриц и матричных операций

1. I – единичная матрица

2. det A – определитель матрицы А. Если det A = 0, то А – вырожденная матрица, иначе А невырождена.

3. Вычисление произведения двух матриц и матрицы на столбец

Пусть даны две матрицы: A размера n строк и m столбцов, B размера m строк и k столбцов, а также столбец Х из m элементов. Надо вычислить произведения С = A×B и Y = A×X.

В основе вычислительных алгоритмов лежат следующие формулы:

; ;

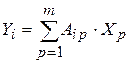
4. A T – транспонированная матрица.

5. Если А – квадратная невырожденная матрица, то A –1 – обратная матрица, такая, что AA –1 = A –1 A = I.

Свойства: (A B) –1 = B –1 A –1 ; (A T ) –1 = (A –1 ) T ; (A Т A) – симметричная матрица.

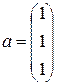
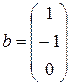
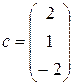
Пусть, например, ; ; . Пример линейной комбинации: 1×a + 1×b + 1×c = .

7. Ненулевые векторы называются линейно зависимыми, если существует их линейная комбинация, равная нулевому вектору.

Пусть, например, ; ; . Векторы x, y, z линейно зависимы, т.к. z = x – y. Отсюда 1×x – 1×y – 1×z = 0.

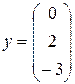
8. Ранг матрицы А – целое число rank A, равное максимальному порядку отличного от 0 минора матрицы.

Например, матрица 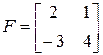невырождена. Следовательно, максимальный порядок её ненулевого минора равен 2, т.е. размерности матрицы. Значит, rank F = 2.

Матрица 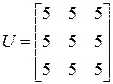имеет ненулевые миноры лишь 1-го порядка, все равные 5. Значит, rank U = 1.

Задачи для самостоятельного решения

1. Дано: . Вычислить det (A) разложением по 1-й строке.

2. Дано: . Вычислить det (A) разложением по 3-му столбцу.

3. Дайте определение понятия «линейная комбинация векторов». Образуйте любую линейную комбинацию из векторов

; ; .

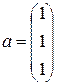
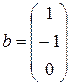
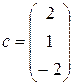
4. Какие векторы называются линейно зависимыми, а какие – линейно независимыми? Являются ли линейно зависимыми следующие три вектора

; ; .

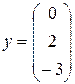
5. Что такое «ранг матрицы»? Чему равны ранги следующих матриц

? Ответ объяснить.

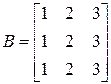
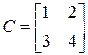
6. Какая из следующих матриц является обратной к матрице C = :

7. Дано: ; . Вычислить B А T A.

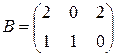
Основные сведения из теории вероятностей

Замечание. Следует отметить, что с точки зрения исследователя, наблюдающего это события, каждый раз условия опыта абсолютно одинаковы, тем не менее, в одном случае событие наступает, а в другом – нет. Это происходит из-за того, что мы не знаем о существовании каких-то факторов, влияющих на событие, или знаем, но не можем их зафиксировать.

Тем не менее, факт наступления случайного события подчиняется определённой закономерности.

Случайная величина x может принимать такие значения, которые можно перенумеровать – х₁, х₂ и т.д. Такие случайные величины называются дискретными. Пример – число очков, выпадающих на игральной кости. Непрерывными называются СВ, возможные значения которых заполняют сплошь некоторую область числовой оси. Пример – значение температуры некоторого тела.

Законы распределения имеют следующие формы.

Для дискретной СВ необходимо задать соответствие между возможными значениями x = х₁, x = х₂, … случайной величины и вероятностями Р(x= х_i) = p_i, с которой эти значения принимаются. Задать это соответствие можно таблично, аналитически (в виде формулы) и графически.

Пример 1.1. Пусть бросаются две игральные кости. СВ x – число выпадений «орла». Очевидно, возможны следующие значения x : х₁ = 0; х₂ = 1; х₃ = 2. Несложно подсчитать, что соответствующие вероятности равны: р₁ = 1/4; р₂ = 1/2; р₃ = 2. Составим таблицу:

которая представляет собой табличное задание закона распределения СВ x = (число выпадения «орла» на двух игральных костях).

Для непрерывной СВ существуют следующие формы записи закона распределения: функция распределения и плотность распределения.

Например, вычислим 0,25-квантиль экспоненциального распределения с параметром l =2, т.е. для распределения с плотностью f(x) = 2exp(-2x). Воспользуемся операторами MathCad

tp:=qexp(0.25, 2) tp = 0.14384

3. Если x и h – независимые СВ, то D[x + h] = D[x] + D[h].

4. Из свойства 2 следует: если x – СВ, то h = – это СВ, у которой D[h] = 1.

Кроме математического ожидания и дисперсии важной числовой характеристикой СВ является коэффициент вариации – безразмерный показатель разброса случайной величины.

Случайные векторы и их характеристики

Набор (x₁,…, x_n) называют также системой случайных величин. Как и обычные (скалярные) случайные величины, случайные векторы бывают непрерывными и дискретными. Исчерпывающей вероятностной характеристикой случайного вектора является его функция распределения (функция совместного распределения системы случайных величин).

Дата добавления: 2019-02-26 ; просмотров: 406 ; Мы поможем в написании вашей работы!

Источник