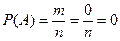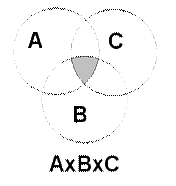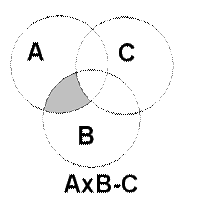что такое случайное событие

Случайное событие

Случа́йное собы́тие — подмножество множества исходов случайного эксперимента; при многократном повторении случайного эксперимента частота наступления события служит оценкой его вероятности.

Случайное событие, которое никогда не реализуется в результате случайного эксперимента, называется невозможным и обозначается символом . Случайное событие, которое всегда реализуется в результате случайного эксперимента, называется достоверным и обозначается символом .

Содержание

Определение

Математически случайное событие — подмножество пространства элементарных исходов случайного эксперимента; элемент алгебры или сигма-алгебры событий , которая в свою очередь задаётся аксиоматически и вместе с пространством элементарных событий и вероятностью образует вероятностное пространство .

Пример

Случайный эксперимент состоит в бросании игральной кости: пример случайного события — выпавшее число чётно; события «Выпала единица», «Выпала двойка» и т. д. — элементарные исходы эксперимента; совокупность всех событий «Выпала 1»..«Выпала 6» — полная группа событий.

См. также

Ссылки

Полезное

Смотреть что такое «Случайное событие» в других словарях:

случайное событие — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] случайное событие Событие, которое при осуществлении некоторых условий может произойти либо не произойти, и для которого имеется определенная… … Справочник технического переводчика

Случайное событие — [ran­dom event, chance event] — событие, которое при осуществлении некоторых условий может произойти либо не произойти, и для которого имеется определенная вероятность его наступления. То же (в разных источниках) исход, случай, результат… … Экономико-математический словарь

СЛУЧАЙНОЕ СОБЫТИЕ — (в теории вероятностей) событие, которое может при осуществлении данных условий (т. е. при данном испытании) как произойти, так и не произойти и для которого имеется определенная вероятность его наступления. Наличие у случайного события… … Большой Энциклопедический словарь

случайное событие — (в теории вероятностей), событие, которое может при осуществлении данных условий (то есть при данном испытании) как произойти, так и не произойти и для которого имеется определенная вероятность его наступления. Наличие у случайного события… … Энциклопедический словарь

случайное событие — atsitiktinis įvykis statusas T sritis fizika atitikmenys: angl. accidental event; chance event; random event vok. zufälliges Ereignis, n rus. случайное событие, n pranc. événement aléatoire, m … Fizikos terminų žodynas

Случайное событие — в теории вероятностей, событие, которое может при данных условиях как произойти так и не произойти и для которого имеется определённая Вероятность р (0 ≤ p ≤ 1) его наступления при данных условиях. Наличие у С. с. А определённой… … Большая советская энциклопедия

СЛУЧАЙНОЕ СОБЫТИЕ — любая комбинация исходов нек рого опыта, имеющая определенную вероятность наступления. Пример 1. При бросании двух игральных костей каждый из 36 исходов опыта может быть представлен нарой (i, j), где i число очков на верхней грани цервой кости, а … Математическая энциклопедия

СЛУЧАЙНОЕ СОБЫТИЕ — (в теории вероятностей), событие, к рое может при осуществлении данных условий (т. е. при данном испытании) как произойти, так и не произойти и для к рого имеется определ. вероятность его наступления. Наличие у С. с. определ. вероятности р… … Естествознание. Энциклопедический словарь

Случайное событие — (в теории вероятностей) событие, которое может, с определенной долей вероятности, в условиях испытания как произойти, так и не произойти; отдельный исход (результат) испытания. См. Случайная величина. Случайный процесс … Начала современного естествознания

событие — Факт, состоящий в том, что нечто произошло или в проблемной области, или в среде, или в информационной системе. [ГОСТ 34.320 96] событие 1. См. Случайное событие. 2. В сетевом планировании и управлении — промежуточный или окончательный… … Справочник технического переводчика

Источник

Что такое случайное событие

Всякое действие, явление, наблюдение с несколькими различными исходами, реализуемое при данном комплексе условий, будем называть испытанием.

Результат этого действия или наблюдения называется событием.

Если событие при заданных условиях может произойти или не произойти, то оно называется случайным. В том случае, когда событие должно непременно произойти, его называют достоверным, а в том случае, когда оно заведомо не может произойти,- невозможным.

События называются несовместными, если каждый раз возможно появление только одного из них.

События называются совместными, если в данных условиях появление одного из этих событий не исключает появление другого при том же испытании.

События называются противоположными, если в условиях испытания они, являясь единственными его исходами, несовместны.

Если полная система состоит из двух несовместных событий, то такие события называются противоположными и обозначаются

Пример. В коробке находится 30 пронумерованных шаров. Установить, какие из следующих событий являются невозможными, достоверными, противоположными:

достали пронумерованный шар (А);

достали шар с четным номером (В);

достали шар с нечетным номером (С);

достали шар без номера (Д).

Какие из них образуют полную группу?

Полную группу событий составляют А и Д, В и С.

Источник

СЛУЧАЙНОЕ СОБЫТИЕ

Смотреть что такое «СЛУЧАЙНОЕ СОБЫТИЕ» в других словарях:

случайное событие — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] случайное событие Событие, которое при осуществлении некоторых условий может произойти либо не произойти, и для которого имеется определенная… … Справочник технического переводчика

Случайное событие — [ran­dom event, chance event] — событие, которое при осуществлении некоторых условий может произойти либо не произойти, и для которого имеется определенная вероятность его наступления. То же (в разных источниках) исход, случай, результат… … Экономико-математический словарь

Случайное событие — Случайное событие подмножество множества исходов случайного эксперимента; при многократном повторении случайного эксперимента частота наступления события служит оценкой его вероятности. Случайное событие, которое никогда не реализуется в… … Википедия

случайное событие — (в теории вероятностей), событие, которое может при осуществлении данных условий (то есть при данном испытании) как произойти, так и не произойти и для которого имеется определенная вероятность его наступления. Наличие у случайного события… … Энциклопедический словарь

случайное событие — atsitiktinis įvykis statusas T sritis fizika atitikmenys: angl. accidental event; chance event; random event vok. zufälliges Ereignis, n rus. случайное событие, n pranc. événement aléatoire, m … Fizikos terminų žodynas

Случайное событие — в теории вероятностей, событие, которое может при данных условиях как произойти так и не произойти и для которого имеется определённая Вероятность р (0 ≤ p ≤ 1) его наступления при данных условиях. Наличие у С. с. А определённой… … Большая советская энциклопедия

СЛУЧАЙНОЕ СОБЫТИЕ — любая комбинация исходов нек рого опыта, имеющая определенную вероятность наступления. Пример 1. При бросании двух игральных костей каждый из 36 исходов опыта может быть представлен нарой (i, j), где i число очков на верхней грани цервой кости, а … Математическая энциклопедия

СЛУЧАЙНОЕ СОБЫТИЕ — (в теории вероятностей), событие, к рое может при осуществлении данных условий (т. е. при данном испытании) как произойти, так и не произойти и для к рого имеется определ. вероятность его наступления. Наличие у С. с. определ. вероятности р… … Естествознание. Энциклопедический словарь

Случайное событие — (в теории вероятностей) событие, которое может, с определенной долей вероятности, в условиях испытания как произойти, так и не произойти; отдельный исход (результат) испытания. См. Случайная величина. Случайный процесс … Начала современного естествознания

событие — Факт, состоящий в том, что нечто произошло или в проблемной области, или в среде, или в информационной системе. [ГОСТ 34.320 96] событие 1. См. Случайное событие. 2. В сетевом планировании и управлении — промежуточный или окончательный… … Справочник технического переводчика

Источник

Теория вероятностей, формулы и примеры

Тема непростая, но если вы собираетесь поступать на факультет, где нужны базовые знания высшей математики, освоить материал — must have. Тем более, все формулы по теории вероятности пригодятся не только в универе, но и при решении 4 задания на ЕГЭ. Начнем!

Основные понятия

Французские математики Блез Паскаль и Пьер Ферма анализировали азартные игры и исследовали прогнозы выигрыша. Тогда они заметили первые закономерности случайных событий на примере бросания костей и сформулировали теорию вероятностей.

Когда мы кидаем монетку, то не можем точно сказать, что выпадет: орел или решка.

Но если подкидывать монету много раз — окажется, что каждая сторона выпадает примерно равное количество раз. Из чего можно сформулировать вероятность: 50% на 50%, что выпадет «орел» или «решка».

Теория вероятностей — это раздел математики, который изучает закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.

Вероятность — это степень возможности, что какое-то событие произойдет. Если у нас больше оснований полагать, что что-то скорее произойдет, чем нет — такое событие называют вероятным.

Ну, скажем, смотрим на тучи и понимаем, что дождь — вполне себе вероятное событие. А если светит яркое солнце, то дождь — маловероятное или невероятное событие.

Случайная величина — это величина, которая в результате испытания может принять то или иное значение, причем неизвестно заранее, какое именно. Случайные величины можно разделить на две категории:

Вероятностное пространство — это математическая модель случайного эксперимента (опыта). Вероятностное пространство содержит в себе всю информацию о свойствах случайного эксперимента, которая нужна, чтобы проанализировать его через теорию вероятностей.

Формулы по теории вероятности

Теория вероятности изучает события и их вероятности. Если событие сложное, то его можно разбить на простые составные части — так легче и быстрее найти их вероятности. Рассмотрим основные формулы теории вероятности.

Случайные события. Основные формулы комбинаторики

Классическое определение вероятности

Вероятностью события A в некотором испытании называют отношение:

P (A) = m/n, где n — общее число всех равновозможных, элементарных исходов этого испытания, а m — количество элементарных исходов, благоприятствующих событию A

Таким образом, вероятность любого события удовлетворяет двойному неравенству:

Пример 1. В пакете 15 конфет: 5 с молочным шоколадом и 10 — с горьким. Какова вероятность вынуть из пакета конфету с белым шоколадом?

Так как в пакете нет конфет с белым шоколадом, то m = 0, n = 15. Следовательно, искомая вероятность равна нулю:

Неприятная новость для любителей белого шоколада: в этом примере событие «вынуть конфету с белым шоколадом» — невозможное.

Пример 2. Из колоды в 36 карт вынули одну карту. Какова вероятность появления карты червовой масти?

Количество элементарных исходов, то есть количество карт равно 36 (n). Число случаев, благоприятствующих появлению карты червовой масти (А) равно 9 (m).

Геометрическое определение вероятности

Геометрическая вероятность события А определяется отношением:

P(A)= m(A)/m(G), где m(G) и m(A) — геометрические меры (длины, площади или объемы) всего пространства элементарных исходов G и события А соответственно

Чаще всего, в одномерном случае речь идет о длинах отрезков, в двумерном — о площадях фигур, а в трехмерном — об объемах тел.

Пример. Какова вероятность встречи с другом, если вы договорились встретиться в парке в промежутке с 12.00 до 13.00 и ждете друг друга 5 минут?

У нас есть отличные курсы по математике для учеников с 1 по 11 классы — приглашаем на вводный урок!

Сложение и умножение вероятностей

Теорема о сложении вероятностей звучит так: вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий:

P(A + B) = P(A) + P(B)

Эта теорема справедлива для любого числа несовместных событий:

Если случайные события A₁, A₂. A_n образуют полную группу несовместных событий, то справедливо равенство:

Произведением событий А и В называется событие АВ, которое наступает тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.

Вторая теорема о сложении вероятностей: вероятность суммы совместных событий вычисляется по формуле:

P(A + B) = P(A) + P(B) − P(AB)

События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Теорема об умножении вероятностей: вероятность произведения независимых событий А и В вычисляется по формуле:

P(AB) = P(A) * P(B)

Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8.

Найдем вероятности того, что формула содержится:

А — формула содержится в первом справочнике;

В — формула содержится во втором справочнике;

С — формула содержится в третьем справочнике.

Воспользуемся теоремами сложения и умножения вероятностей.

Ответ: 1 — 0,188; 2 — 0,452; 3 — 0,336.

Формула полной вероятности и формула Байеса

По теореме умножения вероятностей:

Аналогично, для остальных гипотез:

Эта формула называется формулой Байеса. Вероятности гипотез называются апостериорными вероятностями, тогда как — априорными вероятностями.

Пример. Одного из трех стрелков вызывают на линию огня, он производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго — 0,5; для третьего — 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.

Формула Бернулли

При решении вероятностных задач часто бывает, что одно и тоже испытание повторяется многократно, и исход каждого испытания независит от исходов других. Такой эксперимент называют схемой повторных независимых испытаний или схемой Бернулли.

Примеры повторных испытаний:

Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы. А вероятность появления события А в каждом случае постоянна и не изменяется от испытания к испытанию.

Биномиальное распределение — распределение числа успехов (появлений события).

Пример. Среди видео, которые снимает блогер, бывает в среднем 4% некачественных: то свет плохой, то звук пропал, то ракурс не самый удачный. Найдем вероятность того, что среди 30 видео два будут нестандартными.

Опыт заключается в проверке каждого из 30 видео на качество. Событие А — это какая-то неудача (свет, ракурс, звук), его вероятность p = 0,04, тогда q = 0,96. Отсюда по формуле Бернулли можно найти ответ:

Ответ: вероятность плохого видео приблизительно 0,202. Блогер молодец🙂

Наивероятнейшее число успехов

Биномиальное распределение ( по схеме Бернулли) помогает узнать, какое число появлений события А наиболее вероятно. Формула для наиболее вероятного числа успехов k (появлений события) выглядит так:

Пример. В очень большом секретном чатике сидит 730 человек. Вероятность того, что день рождения наугад взятого участника чата приходится на определенный день года — равна 1/365 для каждого из 365 дней. Найдем наиболее вероятное число счастливчиков, которые родились 1 января.

Формула Пуассона

При большом числе испытаний n и малой вероятности р формулой Бернулли пользоваться неудобно. Например, 0.97 999 вычислить весьма затруднительно.

В этом случае для вычисления вероятности того, что в n испытаниях событие произойдет k раз, используют формулу Пуассона:

Здесь λ = np обозначает среднее число появлений события в n испытаниях.

Эта формула дает удовлетворительное приближение для p ≤ 0,1 и np ≤10.

События, для которых применима формула Пуассона, называют редкими, так как вероятность, что они произойдут — очень мала (обычно порядка 0,001-0,0001).

При больших np рекомендуют применять формулы Лапласа, которую рассмотрим чуть позже.

Пример. В айфоне 1000 разных элементов, которые работают независимо друг от друга. Вероятность отказа любого элемента в течении времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента.

P₁₀₀₀(3) = λ 3 /3! * e −λ = 2 3 /3! * e −2 ≈ 0,18.

Ответ: ориентировочно 0,18.

Теоремы Муавра-Лапласа

Кроме того, пусть P_n(k₁;k₂) — вероятность того, что число появлений события А находится между k₁ и k₂.

Локальная теорема Лапласа звучит так: если n — велико, а р — отлично от 0 и 1, то

Интегральная теорема Лапласа звучит так: если n — велико, а р — отлично от 0 и 1, то

Функции Гаусса и Лапласа обладают свойствами, которые пригодятся, чтобы правильно пользоваться таблицей значений этих функций:

Теоремы Лапласа дают удовлетворительное приближение при npq ≥ 9. Причем чем ближе значения q, p к 0,5, тем точнее данные формулы. При маленьких или больших значениях вероятности (близких к 0 или 1) формула дает большую погрешность по сравнению с исходной формулой Бернулли.

Источник

Случайные события и их вероятности

1. Случайные события

Теория вероятностей— это раздел математики изучающий закономерности массовых случайных событий.

Случайным называется событие, наступление которого нельзя гарантировать. Случайность того или иного события определяется множеством причин, которые существуют объективно, но учесть их все, а также степень их влияния на изучаемое событие, невозможно. К таким случайным событиям относятся: выпадание того или иного числа при бросании игральной кости, выигрыш в лотереи, коли­чество больных, записавшихся на прием к врачу и т.п.

И хотя в каждом конкретном случае трудно предсказать исход испытания, при достаточно большом числе наблюдений можно установить наличие некоторой закономерности. Подбрасывая монету, можно заметить, что число выпадания орла и решки примерно одинаково, а при бросании игральной кости различные грани также появляются, примерно одинаково. Это говорит о том, что случайным явлениям присущи свои закономерности, но они проявляются лишь при большом количестве испытаний. Правильность этого подтверждает закон больших чисел, который лежит в основе теории вероятностей.

Рассмотрим основные термины и понятия теории вероятностей.

Испытанием называется совокупность условий, при которых может произойти данное случайное событие.

События бывают достоверные, невозможные и случайные.

Достоверное событие — это событие, которое в результате испытания непременно должно произойти.

Например,если на игральной кости на всех шести гранях. нанести цифру 1, тогда выпадение цифры 1, при бросании кости, есть событие достоверное.

Например,в ранее рассмотренном примере — это выпадение любой цифры, кроме 1.

Случайное событие — это событие, которое при испытаниях может произойти или не произойти. Те или иные события реализуются с различной возможностью.

События называются несовместными, если в результате данного испытания появление одного из них исключает появление другого.

Например,при бросании монеты выпадение одновременно орла и решки есть события несовместные.

События называются совместными, если в результате данного испытания появление одного из них не исключает появление другого.

Например,при игре в карты появление валета и масти пик — события совместные.

События называются равновозможными, если нет оснований считать, что одно из них происходит чаше, чем другое!

Например,выпадение любой грани игрального кубика есть равновозможные события.

События образуют полную группу событий, если в результате испытания обязательно произойдет хотя бы одно из них и любые два из них несовместны.

Например,при 10 выстрелах в мишень возможно от 0 до 10 попаданий. При бросании игрального кубика может выпасть цифра от 1 до 6. Эти события образуют полную группу.

События, входящие в полную группу попарно несовместных и равновозможных событий, называются исходами, или элементарными событиями. Согласно определению достоверного события, можно считать, что событие, состоящее в появлении одного, неважно какого, из событий полной группы, есть событие достоверное.

Например,при бросании одного игрального кубика выпадает число меньше семи. Это пример достоверного события.

Частным случаем событий, образующих полную группу, являются противоположные события.

Два несовместных события А и 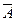(читается «не А») называются противоположными, если в результате испытания одно из них должно обязательно произойти.

Например,если стипендия начисляется только при получении на экзамене хороших и отличных оценок, то события «стипендия» и «неудовлетворительная или удовлетворительная оценка» — противоположные.

Событие А называется благоприятствующим событию В, если появление события А влечет за собой появление события В.

Например,при бросании игрального кубика появлению нечетного числа благоприятствуют события, связанные с выпадением чисел 1,3 и 5.

2. Операции над событиями

Операции над событиями аналогичны операциям над множествами.

Суммой нескольких событий называется событие, состоящее в наступлении хотя бы одного из них в результате испытания.

Сумма событий может быть обозначена знаками «+», «È», «или».

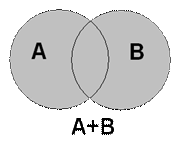
На рисунке 1 представлена геометрическая интерпретация с помощью диаграмм Эйлера-Венна. Сумме событий А + В будет соответствовать вся заштрихованная область.

рис.1

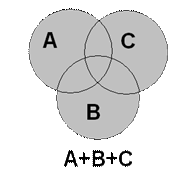
Область пересечения событий А и В соответствует совместным событиям, которые могут произойти одновременно. Аналогично для событий А, В и С имеются совместные события А и В; А и С; В и С; А и В и С, которые могут про изойти одновременно.

Например,в урне находятся белые, красные и синие шары. Возможны следующие события: А — вынут белый шар; В — вынут красный шар; С — вынут синий шар. Событие В + С означает, что произошло событие — вынут цветной шар или вынут не белый шар.

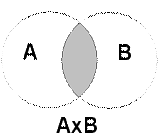
Произведением нескольких событий называется событие которое состоит в совместном наступлении всех этих событий в результате испытания.

Произведение событий может быть обозначено знаками «х», «∩», «и».

Геометрическая интерпретация произведения событий представлена на рис. 2.

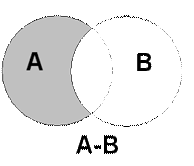
Разностью двух событий А-В называется событие, состоящее из исходов, входящих в А, но не входящих в В.

На рис. 3 представлена иллюстрация разности событий с помощью диаграмм Эйлера-Венна.

Разностью двух событий А-В является заштрихованная область А без той части, которая входит в событие В. Разность между произведением событий А и В и событием С будет совместная площадь события А и события В без совместной с нею площадью события С.

3. Определение вероятности события

Классическое определение вероятности заключается в следующем. Если известны все возможные исходы испытания и нет оснований считать, что одно случайное событие появлялось бы чаще других, т.е. события равновозможны и несовместны, то имеется возможность аналитического определения вероятности события.

Вероятностью Р(А)события Аназывается отношение числа благоприятствующих исходов т к общему числу равновозможных несовместных исходов п:

(1)

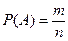
Свойства вероятности:

1. Вероятность случайного события А находится между 0 и 1.

.

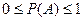
2. Вероятность достоверного события равна 1.

.

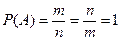
3. Вероятность невозможного события равна 0.

.

Источник