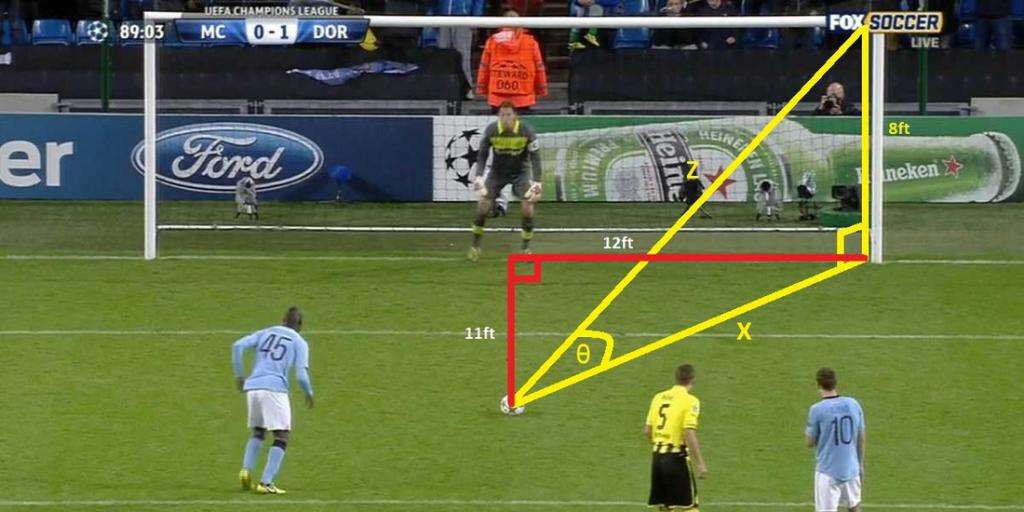
что такое синус в физике
Определение синуса. Основные тригонометрические функции
Тригонометрия является важной частью математики, знания которой широко используются в астрономии и при ориентировании на местности. В данной статье рассматривается определение синуса, косинуса, тангенса и котангенса как основных тригонометрических функций.
Что такое тригонометрия?
Это наука, которая изучает количественные свойства треугольников, о чем говорит ее название. Процесс изучения этих простых плоских фигур осуществляется с использованием так называемых тригонометрических функций.
Еще в древнем Вавилоне и Египте люди сталкивались с задачами, требующими знания соотношения между сторонами и углами треугольника (например, при строительстве египетских пирамид). Однако до нашего времени не дошли точные свидетельства того, что вавилоняне и египтяне располагали необходимой математической теорией для решения задач подобного рода.
Развитие тригонометрия получила на заре нашей эры, благодаря достижениям древнегреческих ученых. Первые таблицы тригонометрических функций были составлены лишь во второй половине XV века.
Прямоугольный треугольник
Перед тем как давать определение синусу и другим тригонометрическим функциям, необходимо пояснить, что представляет собой прямоугольный треугольник. У него один из углов равен 90o.
Зная, что сумма углов в этой фигуре равна 180o, можно с уверенностью сказать, что два других угла в сумме составят 90o. При этом каждый из них будет меньше, чем прямой угол.
Введение тригонометрических функций
Давая определение синуса угла, следует сказать, что он равен отношению отрезка BC к отрезку AB. Записывается это следующим образом: sin(θ) = BC/AB. Поскольку AB = 1, то sin(θ) = BC. Иными словами, под синусом угла прямоугольного треугольника понимают отношение катета, лежащего напротив этого угла, к гипотенузе.
Теперь определение косинуса угла. Это отношение катета, прилежащего к рассматриваемому углу, к гипотенузе. Для рисунка выше имеем: cos(θ) = AC/AB = AC.
Свойства синуса и других тригонометрических функций
Из введенных определений синуса, косинуса угла и других функций следуют несколько важных выводов об их свойствах:
Периодичность функций
Это свойство специально было вынесено в отдельный пункт статьи, поскольку его рассмотрение заслуживает отдельного внимания.
Если вращать отрезок AB (см. рис. выше) против часовой стрелки, то точка B пробежит всю окружность единичного радиуса. Как при этом будут меняться тригонометрические функции?
Рассмотрим синус. Согласно определению синуса угла, когда θ = 0, то BC = 0, то есть sin(0o) = 0. По мере возрастания угла θ, увеличивается длина отрезка BC. При этом длина AB остается неизменной. Это означает, что sin(θ) постоянно увеличивается. Когда угол θ = 90o, то BC=AB и sin(90o) = 1.
Дальнейшее вращение AB против часовой стрелки приводит к уменьшению значения синуса до нуля при угле 180o (sin(180o)=0).
Наконец, в 4-м квадранте окружности, когда угол меняется от 270o до 360o, абсолютное значение синуса увеличивается, но модуль его уменьшается до тех пор, пока при 360o он снова не станет равным нулю (sin(360o) = sin(0o) = 0).
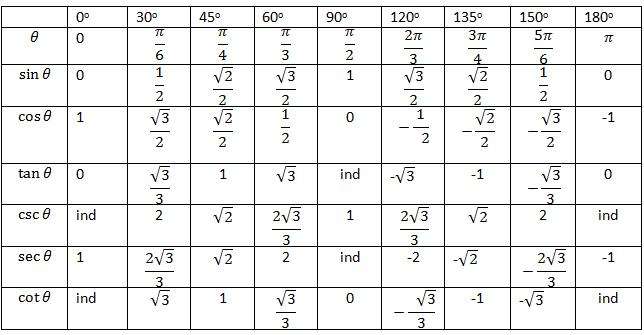
Таблица значений тригонометрических функций
Эта таблица включает в себя данные о значениях синуса, косинуса, тангенса и котангенса для набора углов. Школьников заставляют учить эти значения наизусть.
В настоящее время, благодаря развитию информатики, все языки программирования и калькуляторы снабжены соответствующими библиотеками, которые позволяют быстро рассчитать значения любой тригонометрической функции за доли секунды.
Ниже приводится таблица, в которой приведены значения для всех названных функций набора углов. Которые представлены, как в градусах, так и в радианах. Буквы «ind» означают, что функция для этого угла имеет неопределенное значение. Помимо основных четырех тригонометрических функций, в таблице также приводятся секанс (sec) и косеканс (csc), которые представляют собой обратные косинус и синус, соответственно.
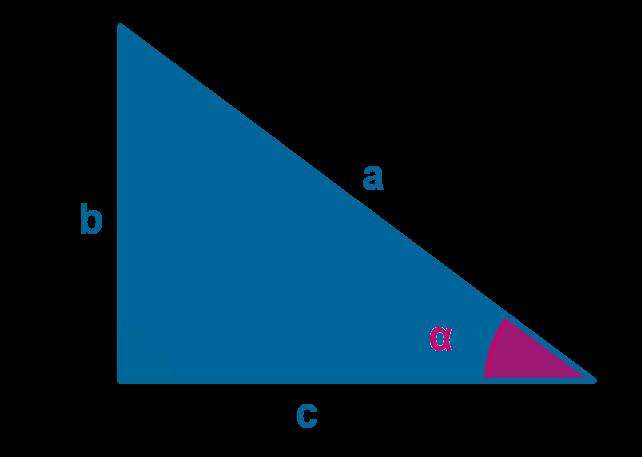
Теорема Пифагора и связь синуса и косинуса
Поскольку определение синуса и косинуса угла основано на использовании прямоугольного треугольника, то эти функции можно связать, если воспользоваться теоремой Пифагора.
Для изображенного выше прямоугольного треугольника имеем: sin(α) = b/a и cos(α) = c/a. Теорема Пифагора записывается так: c2 + b2 = a2. Если левую и правую части этого выражения поделить на a2, а затем подставить формулы для синуса и косинуса, то получим: (sin(α))2 + (cos(α))2 = 1.
Синус, косинус и тангенс острого угла прямоугольного треугольника
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.

Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.
Острый угол — меньший 90 градусов.
Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 🙂
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.
Давайте докажем некоторые из них.
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?
С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
| 0 | |
| 0 | |
| 0 | |
| 0 | − |
| − | 0 |
Обратите внимание на два красных прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.
Ты нашел то, что искал? Поделись с друзьями!
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
Задача решается за четыре секунды.
Найдем по теореме Пифагора.
Треугольник с углами и — равнобедренный. В нем гипотенуза в раз больше катета.
Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.
Основное тригонометрическое тождество
9 класс, 10 класс, ЕГЭ/ОГЭ
Связь между sin и cos одного угла
Вы уже наверняка знаете, что тождественный — это равный.
Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция.
Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:
sin 2 α + cos 2 α = 1
Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.
Равенство tg 2 α + 1 = 1/cos 2 α и равенство 1 + сtg 2 α + 1 = 1/sin 2 α выводят из основного тождества, разделив обе части на sin 2 α и cos 2 α.
В результате деления получаем:
Поэтому основному тригонометрическому тождеству уделяется максимум внимания. Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая.
sin 2 α + cos 2 α = 1
Сумма квадратов синуса и косинуса одного угла тождественно равна единице.
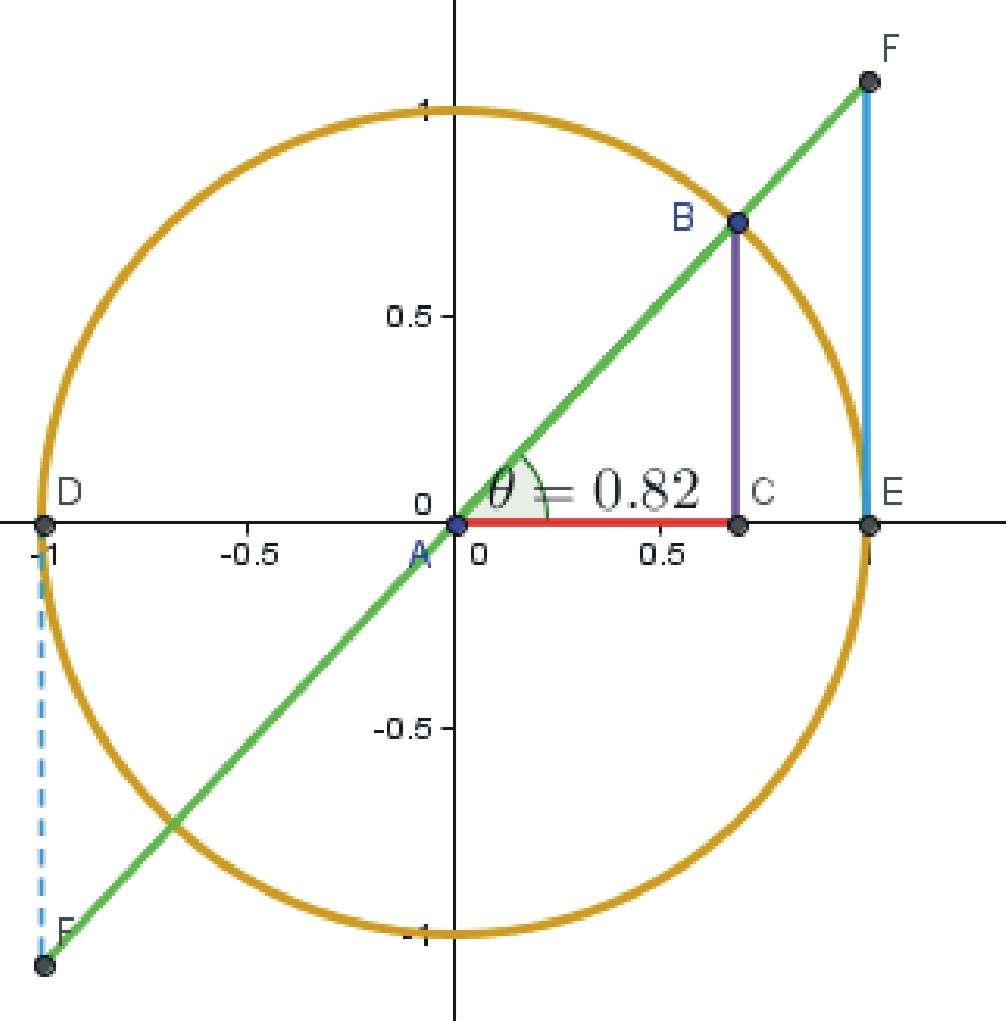
Чтобы доказать тождество, обратимся к теме единичной окружности.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.
Докажем тождество sin 2 α + cos 2 α = 1
Образовался прямоугольный треугольник OA1B.
Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:
Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.
Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.
Тангенс и котангенс через синус и косинус
Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.
Исходя из определений:
Это позволяет сделать вывод, что тригонометрические тождества

задаются sin и cos углов.
Отсюда следует, что тангенс угла — это отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.
Отдельно стоит обратить внимание на то, что тригонометрические тождества

верны для всех углов α, значения которых вписываются в диапазон.
применимо для любого угла α, не равного π * z, где z — это любое целое число.
Связь между тангенсом и котангенсом
Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.
Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.
Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.
tg α * ctg α = 1.
Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.
Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.
Тангенс и косинус, котангенс и синус
Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла — с синусом.
Эта связь становится очевидна, если взглянуть на тождества:
Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.
Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.
Вывести оба этих тождества можно из основного тригонометрического тождества:
sin 2 α + cos 2 α = 1.
Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами.
Основные тригонометрические тождества
sin 2 α + cos 2 α = 1
tg 2 α + 1 =
1 + ctg 2 α =
Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.
Примеры решения задач
Разберем пару задачек, для решения которых нужно знать основные тождества. Рассмотрите внимательно предложенные решения и потренируйтесь самостоятельно.
Задачка 1. Найдите cos α, tg α, ctg α при условии, что sin α = 12/13.
Задачка 2. Найдите значение cos α,
если:
Подставляем значения sin α:
Как видите, задачи решаются достаточно просто, нужно лишь верно применять формулы основных тождеств.
Синус, косинус, тангенс и котангенс (ЕГЭ 2022)
Понятия синуса, косинуса, тангенса, котангенса неразрывно связаны с понятием угла.
Не так страшен черт, как его малюют!
Чтобы хорошо разобраться в этих понятиях (нет, не в чёрте! в тригонометрии 🙂 ), начнём с самого начала.
Синус, косинус, тангенс, котангенс — коротко о главном.
Синус угла — это отношение противолежащего (дальнего) катета к гипотенузе
Косинус угла — это отношение прилежащего (близкого) катета к гипотенузе
Тангенс угла — это отношение противолежащего (дальнего) катета к прилежащему (близкому)
Котангенс угла — это отношение прилежащего (близкого) катета к противолежащему (дальнему).
Понятие угла: радиан, градус
Давай для начала разберёмся в понятии угла.
Посмотрим на рисунок.
Вектор \( AB\) «повернулся» относительно точки \( A\) на некую величину. Так вот мерой этого поворота относительно начального положения и будет выступать угол \( \alpha \).
Что же ещё необходимо знать о понятии угла? Ну, конечно же, единицы измерения угла!
Угол, как в геометрии, так и в тригонометрии, может измеряться в градусах и радианах.
Углом в \( 1<>^\circ \) (один градус) называют центральный угол в окружности, опирающийся на круговую дугу, равную \( \frac<1><360>\) части окружности.
Таким образом, вся окружность состоит из \( 360\) «кусочков» круговых дуг. То есть угол, описываемый окружностью, равен \( 360<>^\circ \).
То есть на рисунке выше изображён угол \( \beta \), равный \( 50<>^\circ \), то есть этот угол опирается на круговую дугу размером \( \frac<50><360>\) длины окружности.
Углом в \( 1\) радиан называют центральный угол в окружности, опирающийся на круговую дугу, длина которой равна радиусу окружности.
Ну что, разобрался? Если нет, то давай разбираться по рисунку.
Итак, на рисунке изображён угол \( \gamma \), равный \( 1\) радиану.
То есть этот угол опирается на круговую дугу, длина которой равна радиусу окружности (длина \( AB\) равна длине \( BB’\) или радиус \( r\) равен длине дуги \( l\)).
Таким образом, длина дуги вычисляется по формуле:
\( l=\theta \cdot r\), где \( \theta \) — центральный угол в радианах.
Ну что, можешь, зная это, ответить, сколько радиан содержит угол, описываемый окружностью?
Да, для этого надо вспомнить формулу длины окружности. Вот она:
Ну вот, теперь соотнесём эти две формулы и получим, что угол, описываемый окружностью равен \( 2\pi \).
То есть, соотнеся величину в градусах и радианах, получаем, что \( 2\pi =360<>^\circ \).
Соответственно, \( \pi =180<>^\circ \).
Как можно заметить, в отличие от «градусов», слово «радиан» опускается, так как единица измерения обычно ясна из контекста.
А сколько радиан составляют \( 60<>^\circ \)?
Уловил? Тогда вперёд закреплять:
Тогда смотри ответы:
Cинус, косинус, тангенс, котангенс угла в прямоугольном треугольнике
Итак, с понятием угла разобрались. А что же всё-таки такое синус, косинус, тангенс, котангенс угла?
Давай разбираться. Для этого нам поможет прямоугольный треугольник.
Как называются стороны прямоугольного треугольника?
Всё верно, гипотенуза и катеты.
Гипотенуза — это сторона, которая лежит напротив прямого угла (в нашем примере это сторона \( AC\))
Катеты – это две оставшиеся стороны \( AB\) и \( BC\) (те, что прилегают к прямому углу).
Причём, если рассматривать катеты относительно угла \( \angle BAC\), то катет \( AB\) – это прилежащий катет, а катет \( BC\) — противолежащий.
Итак, теперь ответим на вопрос: что такое синус, косинус, тангенс и котангенс угла?
Синус угла – это отношение противолежащего (дальнего) катета к гипотенузе.
В нашем треугольнике \( \sin \beta =\frac
Косинус угла – это отношение прилежащего (близкого) катета к гипотенузе.
В нашем треугольнике \( \cos \beta =\frac
Тангенс угла – это отношение противолежащего (дальнего) катета к прилежащему (близкому).
В нашем треугольнике \( tg\beta =\frac
Котангенс угла – это отношение прилежащего (близкого) катета к противолежащему (дальнему).
В нашем треугольнике \( ctg\beta =\frac
Эти определения необходимо запомнить!
Чтобы было проще запомнить какой катет на что делить, необходимо чётко осознать, что в тангенсе и котангенсе сидят только катеты, а гипотенуза появляется только в синусе и косинусе.
А дальше можно придумать цепочку ассоциаций. К примеру, вот такую:
В первую очередь, необходимо запомнить, что синус, косинус, тангенс и котангенс как отношения сторон треугольника не зависят от длин этих сторон (при одном угле).
Тогда убедись, посмотрев на рисунок:
Рассмотрим, к примеру, косинус угла \( \beta \).
По определению, из треугольника \( ABC\): \( \cos \beta =\frac
Но ведь мы можем вычислить косинус угла \( \beta \) и из треугольника \( AHI\): \( \cos \beta =\frac
Видишь, длины у сторон разные, а значение косинуса одного угла одно и то же. Таким образом, значения синуса, косинуса, тангенса и котангенса зависят исключительно от величины угла.
Если разобрался в определениях, то вперёд закреплять их!
Тогда пробуй сам: посчитай то же самое для угла \( \beta \).
Ответы: \( \sin \ \beta =0,6;\ \cos \ \beta =0,8;\ tg\ \beta =0,75;\ ctg\ \beta =\frac<4><3>\).
Единичная (тригонометрическая) окружность
Разбираясь в понятиях градуса и радиана, мы рассматривали окружность с радиусом, равным \( 1\).
Такая окружность называется единичной. Еще ее называют тригонометрической. Это одно и тоже.
Эта окружность — универсальная шпаргалка для решения уравнений и даже неравенств, если уметь ей пользоваться!
У нас есть целая статья, посвященная ей, которая так и называется «Тригонометрическая (единичная) окружность».
Здесь мы тоже ее разберем довольно подробно.
Как можно заметить, данная окружность построена в декартовой системе координат.
Радиус окружности равен единице.
При этом центр окружности лежит в начале координат, начальное положение радиус-вектора зафиксировано вдоль положительного направления оси \( x\) (в нашем примере, это радиус \( AB\)).
Каждой точке окружности соответствуют два числа: координата по оси \( x\) и координата по оси \( y\).
А что это за числа-координаты? И вообще, какое отношение они имеют к рассматриваемой теме?
Для этого надо вспомнить про рассмотренный прямоугольный треугольник.
На рисунке, приведённом выше, можно заметить целых два прямоугольных треугольника.
Рассмотрим треугольник \( ACG\). Он прямоугольный, так как \( CG\) является перпендикуляром к оси \( x\).
Чему равен \( \cos \ \alpha \) из треугольника \( ACG\)?
Всё верно \( \cos \ \alpha =\frac
Кроме того, нам ведь известно, что \( AC\) – это радиус единичной окружности, а значит, \( AC=1\).
Подставим это значение в нашу формулу для косинуса. Вот что получается:
А чему равен \( \sin \ \alpha \) из треугольника \( ACG\)?
Ну конечно, \( \sin \alpha =\frac
Подставим значение радиуса \( AC\) в эту формулу и получим:
Так, а можешь сказать, какие координаты имеет точка \( C\), принадлежащая окружности? Ну что, никак?
А если сообразить, что \( \cos \ \alpha \) и \( \sin \alpha \) — это просто числа?
Какой координате соответствует \( \cos \alpha \)?
Ну, конечно, координате \( x\)!
А какой координате соответствует \( \sin \alpha \)?
Всё верно, координате \( y\)!
Таким образом, точка \( C(x;y)=C(\cos \alpha ;\sin \alpha )\).
А чему тогда равны \( tg \alpha \) и \( ctg \alpha \)?
Всё верно, воспользуемся соответствующими определениями тангенса и котангенса и получим, что \( tg \alpha =\frac<\sin \alpha ><\cos \alpha >=\frac
А что, если угол будет больше \( 90<>^\circ =\frac<\pi ><2>\)?
Вот, к примеру, как на этом рисунке:
Что же изменилось в данном примере?
Давай разбираться. Для этого опять обратимся к прямоугольному треугольнику.
Всё верно, придерживаемся соответствующих определений тригонометрических функций:
Ну вот, как видишь, значение синуса угла всё так же соответствует координате \( y\); значение косинуса угла – координате \( x\); а значения тангенса и котангенса соответствующим соотношениям.
Таким образом, эти соотношения применимы к любым поворотам радиус-вектора.
Уже упоминалось, что начальное положение радиус-вектора – вдоль положительного направления оси \( x\).
До сих пор мы вращали этот вектор против часовой стрелки, а что будет, если повернуть его по часовой стрелке?
Ничего экстраординарного, получится так же угол определённой величины, но только он будет отрицательным.
Таким образом, при вращении радиус-вектора против часовой стрелки получаются положительные углы, а при вращении по часовой стрелке – отрицательные.
Итак, мы знаем, что целый оборот радиус-вектора по окружности составляет \( 360<>^\circ \) или \( 2\pi \).
В первом случае, \( 390<>^\circ =360<>^\circ +30<>^\circ \), таким образом, радиус-вектор совершит один полный оборот и остановится в положении \( 30<>^\circ \) или \( \frac<\pi ><6>\).
Таким образом, из приведённых примеров можем сделать вывод, что углы, отличающиеся на \( 360<>^\circ \cdot m\) или \( 2\pi \cdot m\) (где \( m\) – любое целое число), соответствуют одному и тому же положению радиус-вектора.
Ниже на рисунке изображён угол \( \beta =-60<>^\circ \).
Этот список можно продолжить до бесконечности.
Все эти углы можно записать общей формулой \( \beta +360<>^\circ \cdot m\) или \( \beta +2\pi \cdot m\) (где \( m\) – любое целое число)
Теперь, зная определения основных тригонометрических функций и используя единичную окружность, попробуй ответить, чему равны значения:
Вот тебе в помощь единичная окружность:
Возникли трудности? Тогда давай разбираться.
Отсюда мы определяем координаты точек, соответствующих определённым мерам угла.
Ну что же, начнём по порядку: углу в \( 90<>^\circ =\frac<\pi ><2>\) соответствует точка с координатами \( \left( 0;1 \right)\), следовательно:
\( \text
Зная это, легко определить значения тригонометрических функций в соответствующих точках. Сначала попробуй сам, а потом сверяйся с ответами.
Ответы:
\( \displaystyle \sin \ 180<>^\circ =\sin \ \pi =0\) \( \displaystyle \cos \ 180<>^\circ =\cos \ \pi =-1\) \( \text
\( \text
\( \sin \ 270<>^\circ =-1\) \( \cos \ 270<>^\circ =0\)
\( \text
\( \text
\( \text
\( \sin \ 450<>^\circ =\sin \ \left( 360<>^\circ +90<>^\circ \right)=\sin \ 90<>^\circ =1\) \( \cos \ 450<>^\circ =\cos \ \left( 360<>^\circ +90<>^\circ \right)=\cos \ 90<>^\circ =0\)
\( \text
\( \text
Таким образом, мы можем составить следующую табличку:
Нет необходимости помнить все эти значения!
Достаточно помнить соответствие координат точек на единичной окружности и значений тригонометрических функций:
А вот значения тригонометрических функций углов в \( 30<>^\circ =\frac<\pi ><6>,\ 45<>^\circ =\frac<\pi ><4>\) и \( 30<>^\circ =\frac<\pi ><6>,\ 45<>^\circ =\frac<\pi ><4>\), приведённых ниже в таблице, необходимо запомнить:
Не надо пугаться, сейчас покажем один из примеров довольно простого запоминания соответствующих значений: