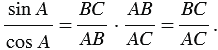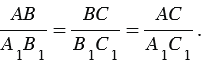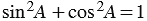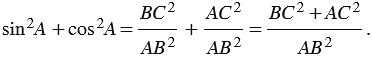что такое синус косинус и тангенс острого угла
Синус, косинус и тангенс острого угла прямоугольного треугольника
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.
Острый угол — меньший 90 градусов.
Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 🙂
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.
Давайте докажем некоторые из них.
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?
С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
| 0 | |
| 0 | |
| 0 | |
| 0 | − |
| − | 0 |
Обратите внимание на два красных прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.
Ты нашел то, что искал? Поделись с друзьями!
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
Задача решается за четыре секунды.
Найдем по теореме Пифагора.
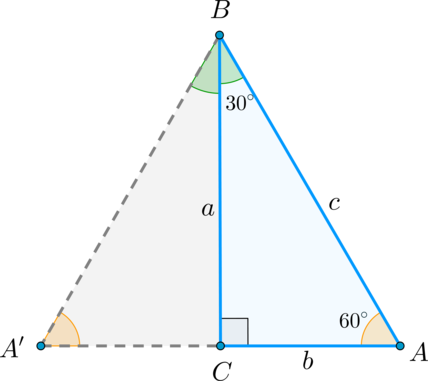
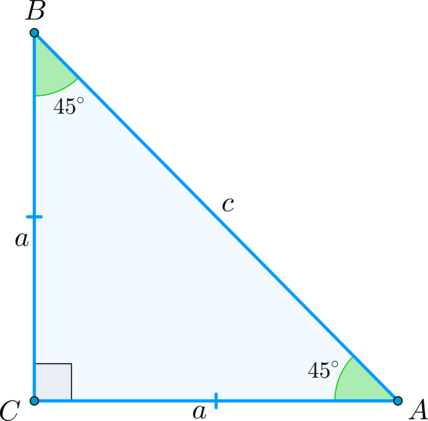
Треугольник с углами и — равнобедренный. В нем гипотенуза в раз больше катета.
Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.
Что такое синус, косинус, тангенс и котангенс в прямоугольном треугольнике?
Синус, косинус и тангенс острого угла прямоугольного треугольника.
Приветствую Вас дорогие учащиеся.
Сейчас рассмотрим что же такое синус, косинус, тангенс и котангенс в прямоугольном треугольнике?
Это тема не сложная, главное это запомнить правила. И так начнем:
Вспомним, что такое прямоугольный треугольник?
Прямоугольным треугольником, называется треугольник у которого один из углов прямой (составляет 90 градусов). Две стороны которые прилежат к прямому углу, называются катетами, а сторона лежащая напротив прямого угла, называется гипотенузой.
Синус (sin(a)) — это отношение противолежащего катета к гипотенузе;
Косинус (cos(a)) — это отношение прилежащего катета к гипотенузе;
Тангенс (tg(a)) — это отношение противолежащего катета к прилежащему катету;
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу;
Котангенс (ctg(a)) — это отношение прилежащего катета к противолежащему.
Другое (равносильное) определение: котангенсом острого угла называется отношение косинуса угла к его синусу;
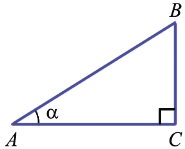
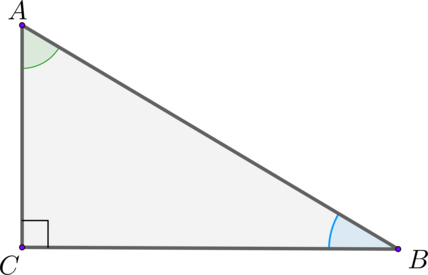
Пусть дан прямоугольный треугольник ABC с прямым углом C.
Найти sin(a); cos(a); tg(a); ctg(a) 
Отношение сторон в прямоугольном треугольнике
Аналогично рассуждаем относительно угла B.
Найти sin(b); cos(b); tg(b); ctg(b) 
Отношение сторон в прямоугольном треугольнике
Пример:
Найти тангенс угла С (tg(C)) треугольника ABC.
Хочешь готовиться к экзаменам бесплатно? Репетитор онлайн бесплатно. Без шуток. ЗДЕСЬ
Синус, косинус и тангенс острого угла прямоугольного треугольника
(1)
(2)
(3)
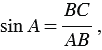
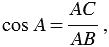
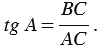
Из формул (1) и (2) получаем:
Сравнивая с формулой (3), находим:
(4)
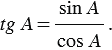
Получили, что тангенс угла равен отношению синуса к косинусу этого угла.
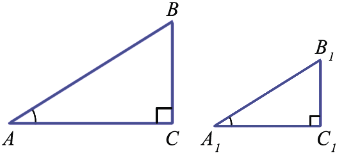
Докажем, что если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.
Доказать: sin A = sin A1, cos A = cos A1, tg A = tg A1.
Доказательство:
Из этих равенств следует, что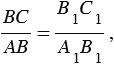 
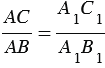
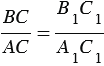
т.е. sin A = sin A1. Аналогично 
, т.е. cos A = cos A1, и 
, т.е. tg A = tg A1, что и требовалось доказать.
Мы получили, что синус, косинус и тангенс острого угла зависит только от величины этого угла.
Докажем основное тригонометрическое тождество:
Из формул (1) и (2) получаем
По теореме Пифагора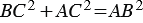 
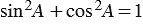
, поэтому 
.
Поделись с друзьями в социальных сетях:
Начальные сведения о синусе, косинусе, тангенсе и котангенсе
Определения
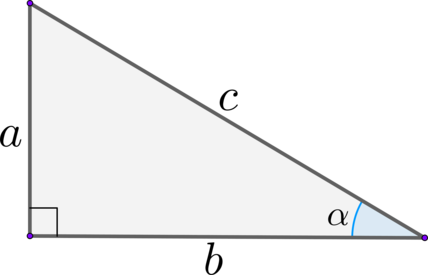
Синус острого угла в прямоугольном треугольнике – это отношение противолежащего к этому углу катета к гипотенузе: \(\sin \alpha=\dfrac ac\)
Косинус острого угла в прямоугольном треугольнике – это отношение прилежащего к этому углу катета к гипотенузе: \(\cos \alpha=\dfrac bc\)
Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего к этому углу катета к прилежащему катету: \(\mathrm
Котангенс острого угла в прямоугольном треугольнике – это отношение прилежащего к этому углу катета к противолежащему катету: \(\mathrm
Утверждение
Синусы, косинусы, тангенсы и котангенсы равных углов соответственно равны.
Теорема
Из определений синуса, косинуса, тангенса и котангенса вытекают следующие формулы:
Утверждение
В прямоугольном треугольнике \(ABC\) с прямым углом \(\angle C\) :
\(\sin \angle A=\cos \angle B\)
Доказательство
Утверждение следует непосредственно из определения синуса и косинуса острого угла в прямоугольном треугольнике.
Теорема
Для углов \(30^\circ, 45^\circ, 60^\circ\) верна следующая таблица:
\[<\large<\begin
Доказательство
Теперь по определению \(\sin \angle A=\sin 60^\circ =\dfrac ac=\dfrac<\sqrt3>2\)
Замечание
Для простоты запоминания таблицы можно записать ее в следующем виде:
Теорема
Справедливы следующие формулы приведения:
\[\begin
Пример
Учащиеся, которые готовятся к сдаче ЕГЭ по математике и при этом рассчитывают на получение конкурентных баллов по итогам его прохождения, непременно должны повторить теорию о синусе, косинусе, тангенсе и котангенсе. Как показывает практика, задания по данной тематике ежегодно встречаются в аттестационном испытании. Таким образом, если одним из ваших слабых мест являются формулы и теоремы синусов, косинусов, тангенсов и котангенсов, рекомендуем освежить в памяти базовую теорию. В этом вам поможет образовательный портал «Школково». В соответствующем разделе представлена теория о синусах, косинусах, тангенсах и котангенсах, которая позволит вам подготовиться к сдаче экзамена. Весь базовый материал составлен нашими специалистами на основе многолетнего опыта и представлен в максимально доступной форме. Ознакомившись с теорией, выпускник сможет грамотно объяснять решение задач ЕГЭ на синусы, косинусы, тангенсы и котангенсы. В этом состоит половина успеха при прохождении аттестационного испытания.
Для того чтобы учащиеся из Москвы или другого населенного пункта России, посетившие наш ресурс, смогли легко и качественно подготовиться к ЕГЭ, мы не только в понятной форме изложили теорию косинусов, синусов, тангенсов и котангенсов, но и подобрали соответствующие упражнения. Для каждого из них наши специалисты прописали подробный алгоритм решения и правильный ответ. Выполняя такие задачи при подготовке к ЕГЭ по математике, выпускники смогут лучше закрепить изученную теорию синусов и косинусов в треугольнике. Выбрать простые и более сложные упражнения вы можете в разделе «Каталог».
Изучив теорию о синусах, косинусах, тангенсах и котангенсах и попрактиковавшись в решении задач по данной теме при подготовке к ЕГЭ, учащиеся имеют возможность сохранить любое задание в «Избранное», чтобы при необходимости обсудить его с преподавателем.
Инструменты пользователя
Инструменты сайта
Боковая панель
Навигация
Загрузки всякие
Связь
Содержание
Синус, косинус, тангенс острого угла
Тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника.
Основное тригонометрическое тождество
Если мы возьмем гипотенузу, равную 1, то это определение можно упростить до:
Тогда теорему Пифагора можно переформулировать так:
$$(\sin \alpha)^2 + (\cos \alpha)^2 = 1$$
Или другая форма записи без скобок:
$$\sin^2 \alpha + \cos^2 \alpha = 1$$
Формулы приведения для острого угла
Возрастание и убывание
Чем больше один из острых углов прямоугольного треугольника, тем меньше другой. Отсюда следует, с учетом ОТТ, для этих углов:
Мнемоническое правило
Правило для косинуса
Синусу не остается ничего другого, кроме «противолежать».
«Длинный» косинус в паре с «коротким» прилежащим катетом, «короткий» синус в паре с «длинным» противолежащим катетом.
Правило для ОТТ
В семье Синичкиных (Sin) праздник. К ним в отпуск приезжает дочка с мужем, семья Косичкиных (Cos). Вот двое Синичкиных радостно бегут навстречу Косичкиным. Они обнимаются (+). И образуют одну большую семью: 1.
Синус в строительстве
Возьмите 10-метровый столб и поднимите его с земли на 45 градусов. Верхушка столба будет находиться на высоте
А 8-метровый столб будет на высоте
Подобные манипуляции со столбами очень полезны в строительстве (пирамиды сами себя не рассчитают). К сожалению, спустя тысячи лет у нас твердо закрепилась мысль, что смысл синуса в возможности вычислить высоту треугольника по гипотенузе и углу. Для краткости мыслительного процесса думаем «синус=высота». Это нормально, главное не застревать на этом, а смотреть шире.
Расчеты в Excel
Пусть известно расстояние до дерева. Нужно узнать его высоту:
