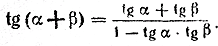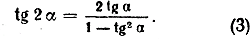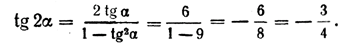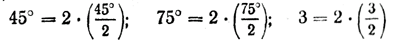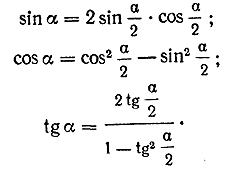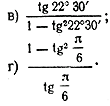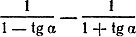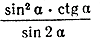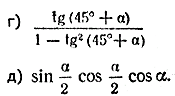что такое синус двойного угла

Способы преобразования

Чтобы понять, как выражаются тригонометрические функции двойных углов, необходимо воспользоваться их записью в виде nα, где n принадлежит натуральному числу. Значение основного выражения отображается математически без скобок. Используя это свойство, можно составить следующее уравнение: sin nα = sin (nα).

Для приведения произведения sin nα х sin nα, используется аналогичное свойство. Выражение можно упростить до 2 (n sin α). Основой тождества является n sin α. В математике используются и другие равенства:

Доказательства равенств

Чтобы подтвердить уравнения на сложение, вычитание и умножение, понадобится подойти к доказательству комплексным способом. Используя формулы синуса с плюсом для углов (α+β) и косинуса ​ для β и α, получится синусα·косинусβ+косинусα·синусβ. Пример для вычитания: соsα ·cosβ-синусα·синусβ.

При вычислении разницы следует придерживаться аналогичного принципа. Результат будет следующим: косинус (α+α) равен двойному значению косинуса минус двойное значение синуса. Формула двойного угла косинуса и синуса доказана. При решении задач из дидактических материалов используются и другие уравнения при положительном и отрицательном значении альфа, при нуле либо половинном π.

Для их доказательства необходимо находить корень из числа z, возводить целое значение в квадрат либо иную степень. Чтобы определиться с ходом решения, необходимо следить за графиком функции:

Сложные действия вычисляются с помощью калькулятора. Если задача состоит из нескольких частей, для нахождения результата потребуется преобразовать первичное уравнение в более простое. Используются следующие равенства:

Решение задач

Задача 1: дан угол, отличный от 2α, например 3π5. Нужно найти его значение. Решение: угол 3π5 необходимо преобразовать. Получается α = 3π5:2 = 3π10. Из результата следует, что ФДУ для косинуса принимает следующий вид: cos3π5 = cos23π10 — sin23π10.

Задача 2: необходимо представить sin2α3 через функции, когда α = 6. Решение: заменить 2α3 = 4·α6. Если подставить данные, получится sin2α3. Выражая через функцию, принимая формулу двойного угла, записывается выражением: sin2α3 = 2·sinα3·cosα3. Используя cosα3, применяя sin2α2, получится результат sin2α3 = 4·sinα6·cos3α6 − 4·sin3α6·cosα6.

Тождества при других значениях

По такой же методике выводятся формулы четвёртой степени. Значение 4α нужно представить в виде 2·2α. Равенство выводится с помощью ФДУ дважды. Для получения равенства пятой степени представляется значение угла 5α в виде 3α+2α.

Такая сумма позволяет использовать формулы двойного и тройного углов с целью преобразования в конечный результат. По аналогичной схеме преобразовываются разные степени тригонометрических функций, но их применяют в тригонометрии редко.

Область применения

Чтобы определить значение тригонометрической функции (ТФ), рассматривается окружность с радиусом в единицу и диаметрами, взаимно перпендикулярными. Для вычислений потребуется отложить от точки, принадлежащей окружности, дуги любых длин. Они будут положительными, если их отложить против часовой стрелки.

Отрицательное значение принимают те, которые размещены по часовой стрелке. Если конец дуги имеет длину f, тогда проекция радиуса на любом диаметре примет значение косинуса дуги. Под аргументом понимается число, которое рассматривается геометрически как f либо радианная мера угла. Если аргумент ТФ взят за угол, тогда его значение выражается и в градусах.

Доказано, что значение острых углов больше нуля, но меньше p/2. Для таких величин ТФ рассматривается как отношение катетов к гипотенузе. Эти элементы принадлежат прямоугольному треугольнику. Название связано с наличием угла в 90 градусов. Для решения задач с тригонометрическими функциями используется и теорема Пифагора, в основе которой находится свойство прямоугольного треугольника: квадрат гипотенузы равен сумме квадратов катетов.

Дуга делит окружность на несколько частей. Углы, размещенные в первой четверти, больше нуля, во второй косинус меньше, но синус больше, в третьей ТФ меньше 0, а в четвёртой получаются значения, противоположные второй. Для построения окружности потребуется циркуль, а для измерения углов транспортир.

Для получения точного чертежа рекомендуется наносить данные на миллиметровую бумагу либо тетрадь в клетку.

Источник

Формулы двойного угла — значения функций, свойства и примеры решений

На уроках математики школьники 8−11 классов изучают интегралы, знакомятся с таблицей значений аргумента (переменная). Через формулу двойного угла (ФДУ) выражаются косинус, синус, тангенс, котангенс с произведением 2α. В основе находится тригонометрическая функция угла альфа. Чтобы её отобразить на графике, используются координаты и окружность.

Способы преобразования

Чтобы понять, как выражаются тригонометрические функции двойных углов, необходимо воспользоваться их записью в виде nα, где n принадлежит натуральному числу. Значение основного выражения отображается математически без скобок. Используя это свойство, можно составить следующее уравнение: sin nα = sin (nα).

Для приведения произведения sin nα х sin nα, используется аналогичное свойство. Выражение можно упростить до 2 (n sin α). Основой тождества является n sin α. В математике используются и другие равенства:

В геометрии и алгебре чаще применяются следующие известные формулы: синус2α = cos2α — sin2α, cos2α = 1 − 2·sin2α. Можно разложить производные sin и cos, если угол имеет любой градус. Решение тангенса потребуется, если в основе задачи находится tg2α, при этом значение угла отлично от суммы π4 и π2. Частный случай, когда в задании есть целое число z, а α ≠ π4 + π2·z. Если рассматривать для котангенса ФДУ при любом альфа, ctg2α не определён на промежутке π2. Для косинуса двойного угла характерна тройная запись.

Доказательства равенств

Чтобы подтвердить уравнения на сложение, вычитание и умножение, понадобится подойти к доказательству комплексным способом. Используя формулы синуса с плюсом для углов (α+β) и косинуса ​ для β и α, получится синусα·косинусβ+косинусα·синусβ. Пример для вычитания: соsα ·cosβ-синусα·синусβ.

При вычислении разницы следует придерживаться аналогичного принципа. Результат будет следующим: косинус (α+α) равен двойному значению косинуса минус двойное значение синуса. Формула двойного угла косинуса и синуса доказана. При решении задач из дидактических материалов используются и другие уравнения при положительном и отрицательном значении альфа, при нуле либо половинном π.

Для их доказательства необходимо находить корень из числа z, возводить целое значение в квадрат либо иную степень. Чтобы определиться с ходом решения, необходимо следить за графиком функции:

Сложные действия вычисляются с помощью калькулятора. Если задача состоит из нескольких частей, для нахождения результата потребуется преобразовать первичное уравнение в более простое. Используются следующие равенства:

Их можно привести к косинус2α — синус2α. Если заменить единицу суммой квадратов, тогда sin2α + cos2α = 1. Получается, что синус2α + косинус2α = 1. Подставив данные, выходит: 1 − 2·sin2α.

Чтобы доказать ФДУ котангенса, применяется равенство ctg2α = cos2αsin2α. Преобразовав данные, получится для tg2α равенство 2·sinα·cosαcos2α — sin2α. Разделив выражение на cos2α, отличное от нуля, получится, что tgα определен. Другое выражение поделится на sin2α. Значение sin2α ≠ 0 будет иметь смысл при любом α, если ctg2α имеет смысл.

Решение задач

Для убеждения в справедливости 2α для α=30° применяется значение тригонометрических функций для углов. Если α=30°, тогда 2α будет соответствовать 60°. Необходимо проверить значение sin 60° = 2·sin 30°·cos 30°, cos 60° = cos2 30° — sin2 30°. Если подставить данные, получится подробная функция: tg 60°= 2·tg 30°1 — tg2 30° и ctg 60° = ctg230° — 12·ctg 30°.

Так как sin 30° = 12, cos 30° = 32, tg 30° = 33, ctg 30° = 3 и sin 60° = 32, cos 60° = 12, tg 60° = 3, ctg 60° = 33, тогда выводится следующее: 2·sin 30°·cos 30° = 2·12·32 = 32, cos230° — sin230° = (32)2-(12)2 = 12,2·tg 30°1-tg230° = 2·321 — (33) = 3 и ctg230° — 12·ctg 30° = (3)2 − 12·3 = 33.

Задача 1: дан угол, отличный от 2α, например 3π5. Нужно найти его значение. Решение: угол 3π5 необходимо преобразовать. Получается α = 3π5:2 = 3π10. Из результата следует, что ФДУ для косинуса принимает следующий вид: cos3π5 = cos23π10 — sin23π10.

Задача 2: необходимо представить sin2α3 через функции, когда α = 6. Решение: заменить 2α3 = 4·α6. Если подставить данные, получится sin2α3. Выражая через функцию, принимая формулу двойного угла, записывается выражением: sin2α3 = 2·sinα3·cosα3. Используя cosα3, применяя sin2α2, получится результат sin2α3 = 4·sinα6·cos3α6 − 4·sin3α6·cosα6.

Тождества при других значениях

На практике студенты высших учебных заведений математических факультетов встречаются с задачами, для решения которых применяются формулы тройного, четверного и другого угла. В их основе находятся тригонометрические функции. Чтобы их вывести, используются формулы сложения двойного угла: sin3α = sin (2α+α) = 3·sinα·cos2α — sin3α.

При замене cos2α на 1-sin2α формула примет новый вид: sin3α = 3·sinα-4·sin3α. По аналогичной схеме приводится формула косинуса тройного угла: косинус3α = косинус (2α+α) = косинус3α — 3·синус2α·косинусα.

По такой же методике выводятся формулы четвёртой степени. Значение 4α нужно представить в виде 2·2α. Равенство выводится с помощью ФДУ дважды. Для получения равенства пятой степени представляется значение угла 5α в виде 3α+2α.

Такая сумма позволяет использовать формулы двойного и тройного углов с целью преобразования в конечный результат. По аналогичной схеме преобразовываются разные степени тригонометрических функций, но их применяют в тригонометрии редко.

Область применения

Чтобы определить значение тригонометрической функции (ТФ), рассматривается окружность с радиусом в единицу и диаметрами, взаимно перпендикулярными. Для вычислений потребуется отложить от точки, принадлежащей окружности, дуги любых длин. Они будут положительными, если их отложить против часовой стрелки.

Отрицательное значение принимают те, которые размещены по часовой стрелке. Если конец дуги имеет длину f, тогда проекция радиуса на любом диаметре примет значение косинуса дуги. Под аргументом понимается число, которое рассматривается геометрически как f либо радианная мера угла. Если аргумент ТФ взят за угол, тогда его значение выражается и в градусах.

Доказано, что значение острых углов больше нуля, но меньше p/2. Для таких величин ТФ рассматривается как отношение катетов к гипотенузе. Эти элементы принадлежат прямоугольному треугольнику. Название связано с наличием угла в 90 градусов. Для решения задач с тригонометрическими функциями используется и теорема Пифагора, в основе которой находится свойство прямоугольного треугольника: квадрат гипотенузы равен сумме квадратов катетов.

Дуга делит окружность на несколько частей. Углы, размещенные в первой четверти, больше нуля, во второй косинус меньше, но синус больше, в третьей ТФ меньше 0, а в четвёртой получаются значения, противоположные второй. Для построения окружности потребуется циркуль, а для измерения углов транспортир.

Для получения точного чертежа рекомендуется наносить данные на миллиметровую бумагу либо тетрадь в клетку.

Источник

Тригонометрические формулы: косинус, синус и тангенс двойного угла

Формулы двойного угла дают возможность выразить тригонометрические функции (синус, косинус, тангенс, котангенс) угла ` 2\alpha` через эти самые функции угла `\alpha`.

Перечень всех формул двойного угла

Записанный ниже список — это основные формулы двойного угла, которые наиболее часто используются в тригонометрии. Для косинуса их есть три, они все равносильны и одинаково важны.

`sin \ 2\alpha=` `2 \ sin \ \alpha \ cos \ \alpha`
`cos \ 2\alpha=cos^2 \alpha-sin^2 \alpha`, ` cos \ 2\alpha=1-2 \ sin^2 \alpha`, `cos \ 2\alpha=2 \ cos^2 \alpha-1`
`tg \ 2\alpha=\frac<2 \ tg \alpha><1-tg^2 \alpha>`
`ctg \ 2\alpha=\frac<2 \ ctg \alpha>`

Следующие тождества выражают все тригонометрические функции угла ` 2\alpha` через функции тангенс и котангенс угла `\alpha`.

Формулы для косинуса и синуса двойного угла выполняются для любого угла `\alpha`. Формулы для тангенса двойного угла справедливы для тех `\alpha`, при которых определен `tg \ 2\alpha`, то есть при ` \alpha\ne\frac\pi4+\frac\pi2 n, \ n \in Z`. Аналогично, для котангенса они имеют место для тех `\alpha`, при которых определен `ctg \ 2\alpha`, то есть при ` \alpha\ne\frac\pi2 n, \ n \in Z`.

Доказательство формул двойного угла

Все формулы двойного угла выводятся из формул сумы и разности углов тригонометрических функций.

Возьмем две формулы, для сумы углов синуса и косинуса:

`sin(\alpha+\beta)=` `sin \ \alpha\ cos \ \beta+cos \ \alpha\ sin \ \beta` и `cos(\alpha+\beta)=` `cos \ \alpha\ cos \ \beta-sin \ \alpha\ sin \ \beta`. Возьмем `\beta=\alpha`, тогда `sin(\alpha+\alpha)=` `sin \ \alpha\ cos \ \alpha+cos \ \alpha\ sin \ \alpha=2 \ sin \ \alpha \ cos \ \alpha`, аналогично `cos(\alpha+\alpha)=` `cos \ \alpha\ cos \ \alpha-sin \ \alpha\ sin \ \alpha=cos^2 \alpha-sin^2 \alpha`, что и доказывает формулы двойного угла для синуса и косинуса.

Два другие равенства для косинуса ` cos \ 2\alpha=1-2 \ sin^2 \alpha` и `cos \ 2\alpha=2 \ cos^2 \alpha-1` сводятся к уже доказанному, если в них заменить 1 на `sin^2 \alpha+cos^2 \alpha=1`. Так `1-2 \ sin^2 \alpha=` `sin^2 \alpha+cos^2 \alpha-2 \ sin^2 \alpha=` `cos^2 \alpha-sin^2 \alpha` и `2 \ cos^2 \alpha-1=` `2 \ cos^2 \alpha-(sin^2 \alpha+cos^2 \alpha)=` `cos^2 \alpha-sin^2 \alpha`.

Чтобы доказать формулы тангенса двойного угла и котангенса, воспользуемся определением этих функций. Запишем `tg \ 2\alpha` и `ctg \ 2\alpha` в виде `tg \ 2\alpha=\frac ` и `ctg \ 2\alpha=\frac `. Применив уже доказанные формулы двойного угла для синуса и косинуса, получим `tg \ 2\alpha=\frac =\frac <2 \ sin \alpha cos>` и `ctg \ 2\alpha=\frac =` `\frac <2 \ sin \alpha cos>`.

В случае с тангенсом разделим числитель и знаменатель конечной дроби на `cos^2 \alpha`, для котангенса в свою очередь — на `sin^2 \alpha`.

Предлагаем еще посмотреть видео, чтобы лучше закрепить теоретический материал:

Примеры использования формул при решении задач

Формулы двойного угла в большинстве случаев используются для преобразование тригонометрических выражений. Рассмотрим некоторые из случаем, как можно на практике применять их при решений конкретных задач.

Пример 1. Проверить справедливость тождеств двойного угла для `\alpha=30^\circ`.

Решение. В наших формулах используется два угла `\alpha` и `2\alpha`. Значение первого угла задано в условии, второго соответственно будет `2\alpha=60^\circ`. Также нам известны числовые значения для всех тригонометрических функций этих углов. Запишем их:

`sin 30^\circ=\frac 1 2`, `cos 30^\circ=\frac <\sqrt 3>2`, `tg 30^\circ=\frac <\sqrt 3>3`, `ctg 30^\circ=\sqrt 3` и

`sin 60^\circ=\frac <\sqrt 3>2`, `cos 60^\circ=\frac 1 2`, `tg 60^\circ=\sqrt 3`, `ctg 60^\circ=\frac <\sqrt 3>3`.

`sin 60^\circ=2 sin 30^\circ cos 30^\circ=` `2 \cdot \frac 1 2 \cdot \frac <\sqrt 3>2=\frac <\sqrt 3>2`,

`cos 60^\circ=cos^2 30^\circ-sin^2 30^\circ=` `(\frac <\sqrt 3>2)^2 \cdot (\frac 1 2)^2=\frac 1 2`,

Что и доказывает справедливость равенств для заданного в условии угла.

Пример 2. Выразить `sin \frac <2\alpha>3` через тригонометрические функции угла `\frac <\alpha>6`.

Решение. Запишем угол синуса следующим образом ` \frac <2\alpha>3=4 \cdot \frac <\alpha>6`. Тогда, применив два раза формулы двойного угла, мы сможем решить нашу задачу.

Вначале воспользуемся равенством синуса двойного угла: ` sin\frac <2\alpha>3=2 \cdot sin\frac <\alpha>3 \cdot cos\frac <\alpha>3 `, теперь снова применим наши формулы для синуса и косинуса соответственно. В результате получим:

` sin\frac <2\alpha>3=2 \cdot sin\frac <\alpha>3 \cdot cos\frac <\alpha>3=` `2 \cdot (2 \cdot sin\frac <\alpha>6 \cdot cos\frac <\alpha>6) \cdot (cos^2\frac <\alpha>6-sin^2\frac <\alpha>6)=` `4 \cdot sin\frac <\alpha>6 \cdot cos^3 \frac <\alpha>6-4 \cdot sin^3\frac <\alpha>6 \cdot cos \frac <\alpha>6`.

Ответ. ` sin\frac <2\alpha>3=` `4 \cdot sin\frac <\alpha>6 \cdot cos^3 \frac <\alpha>6-4 \cdot sin^3\frac <\alpha>6 \cdot cos \frac <\alpha>6`.

Формулы тройного угла

Эти формулы, аналогично к предыдущим, дают возможность выразить функции угла ` 3\alpha` через эти самые функции угла `\alpha`.

Доказать их можно, используя равенства сумы и разности углов, а также хорошо известные нам формулы двойного угла.

`sin \ 3\alpha= sin (2\alpha+ \alpha)=` `sin 2\alpha cos \alpha+cos 2\alpha sin \alpha=` `2 sin \alpha cos \alpha cos \alpha+(cos^2 \alpha-sin^2 \alpha) sin \alpha=` `3 sin \alpha cos^2 \alpha-sin^3 \alpha`.

Заменим в полученной формуле `sin \ 3\alpha=3 sin \alpha cos^2 \alpha-sin^3 \alpha` `cos^2\alpha` на `1-sin^2\alpha` и получим `sin \ 3\alpha=3 \ sin \ \alpha-4sin^3 \alpha`.

Также и для косинуса тройного угла:

`cos \ 3\alpha= cos (2\alpha+ \alpha)=` `cos 2\alpha cos \alpha-sin 2\alpha sin \alpha=` `(cos^2 \alpha-sin^2 \alpha) cos \alpha-2 sin \alpha cos \alpha sin \alpha+=` `cos^3 \alpha-3 sin^2 \alpha cos \alpha`.

Заменив в конечном равенстве `cos \ 3\alpha=cos^3 \alpha-3 sin^2 \alpha cos \alpha` `sin^2\alpha` на `1-cos^2\alpha`, получим `cos \ 3\alpha=4cos^3 \alpha-3 \ cos \ \alpha`.

С помощью доказанных тождеств для синуса и косинуса можно доказать для тангенса и котангенса:

Для доказательства формул угла ` 4\alpha` можно представить его как ` 2 \cdot 2\alpha` и примерить два раза формулы двойного угла.

Для вывода аналогичных равенств для угла ` 5\alpha` можно записать его, как ` 3\alpha + 2\alpha` и применить тождества суммы и разности углов и двойного и тройного угла.

Аналогично выводятся все формулы для других кратных углов, то нужны они на практике крайне редко.

Источник

Что такое синус двойного угла

Тригонометрические функции двойного угла

sin (α + β) = sin α • cos β + sin β • cos α.

sin 2 α = sin α • cos α + sin α • cos α = 2 sin α cos α .

sin 2 α = 2 sin α cos α (1)

Синус двойного угла равен удвоенному произведению синуса данного угла на его косинус.

Аналогично, положив в формуле

cos (α + β) = cos α cos β — sin α sin β,

Косинус двойного угла равен квадрату косинуса данного угла минус квадрат синуса того же угла.

Точно так же, положив в формуле

Тангенс двойного угла равен удвоенному тангенсу данного угла, деленному на единицу минус квадрат тангенса того же угла.

1) Пусть sin α = 0,6, причем угол α оканчивается во 2-й четверти.

Тогда cos α = — \ / 1 — sin 2 α = — \ / 1 — 0,36 = — 0,8.

sin 2 α = 2 sin α • cos α = 2 • 0,6 • (— 0,8) = — 0,96;

cos 2 α = cos 2 α — sin 2 α = 0,64 — 0,36 = 0,28.

Замечание. Не следует думать, что двойной угол обязательно содержит четное число градусов или радианов: 20°; 60°; 4; 6 и т. д. Под двойным углом можно понимать любой угол. Например,

Эти формулы выражают тригонометрические функции угла через тригонометрические функции половинного угла.

а) sin α > 0, sin 2 α > 0; в) sin α α > 0;

а) sin 22°30′ • cos 22e30′;

б) cos 2 22°30′ — sin 2 22°30′;

а) (sin α + cos α ) 2 = 1 + sin 2 α ;

б) cos 4 α — sin 4 α = cos 2 α ;

7. Доказать, что для любого острого угла α

a). sin 2 ( β — 45°) — cos 2 ( β — 45°).

в).

11. Выразить sin α и cos α :

а) через sin α /₂ и cos α /₂ ;

а).

в). 2 cos 2 α — cos 2 α

в). cos ( 2arcsin 1 /₂ )

14. Найти формулу общего членa арифметической прогрессии, для которой
а ₁ = cos 2φ; а ₂ = cos 2 φ

15. Доказать, что бесконечная геометрическая прогрессия, у которой
а ₁ = 4sin φ, а ₂ = sin 2φ, является бесконечно убывающей, и найти ее сумму.

Источник

Тригонометрические формулы. Их вывод

Наиболее часто встречающиеся тригонометрические формулы:

\(\blacktriangleright\) Основные тождества: \[\begin <|l|l|>\hline \sin^2 \alpha+\cos^2 \alpha =1& \mathrm\, \alpha \cdot \mathrm\, \alpha =1 \\ &(\sin\alpha\ne 0, \cos\alpha\ne 0)\\[0.5ex] \hline &\\ \mathrm\, \alpha=\dfrac<\sin \alpha> <\cos \alpha>&\mathrm\, \alpha =\dfrac<\cos \alpha> <\sin \alpha>\\&\\ 1+\mathrm^2\, \alpha =\dfrac1 <\cos^2 \alpha>& 1+\mathrm^2\, \alpha=\dfrac1<\sin^2 \alpha>\\&\\ (\cos\alpha\ne 0)& (\sin\alpha\ne 0) \\ \hline \end\]

\(\blacktriangleright\) Формулы сложения углов: \[\begin <|l|r|>\hline &\\ \sin<(\alpha\pm \beta)>=\sin\alpha\cdot \cos\beta\pm \sin\beta\cdot \cos\alpha & \cos<(\alpha\pm \beta)>=\cos\alpha\cdot \cos\beta \mp \sin\alpha\cdot \sin\beta\\ &\\ \hline &\\ \mathrm\, (\alpha\pm \beta)=\dfrac<\mathrm\, \alpha\pm \mathrm\, \beta><1 \mp \mathrm\, \alpha\cdot \mathrm\, \beta> & \mathrm\, (\alpha\pm\beta)=-\dfrac<1\mp \mathrm\, \alpha\cdot \mathrm\, \beta><\mathrm\, \alpha\pm \mathrm\, \beta>\\&\\ \cos\alpha\cos\beta\ne 0&\sin\alpha\sin\beta\ne 0\\ \hline \end\]

\(\blacktriangleright\) Формулы понижения степени: \[\begin <|lc|cr|>\hline &&&\\ \sin^2\alpha=\dfrac<1-\cos<2\alpha>>2 &&& \cos^2\alpha=\dfrac<1+\cos<2\alpha>>2\\&&&\\ \hline \end\]

\(\blacktriangleright\) Формулы произведения функций: \[\begin <|c|>\hline \\ \sin\alpha\sin\beta=\dfrac12\bigg(\cos<(\alpha-\beta)>-\cos<(\alpha+\beta)>\bigg)\\\\ \cos\alpha\cos\beta=\dfrac12\bigg(\cos<(\alpha-\beta)>+\cos<(\alpha+\beta)>\bigg)\\\\ \sin\alpha\cos\beta=\dfrac12\bigg(\sin<(\alpha-\beta)>+\sin<(\alpha+\beta)>\bigg)\\\\ \hline \end\]

\(\blacktriangleright\) Выражение синуса и косинуса через тангенс половинного угла: \[\begin <|l|r|>\hline &\\ \sin<2\alpha>=\dfrac<2\mathrm\, \alpha><1+\mathrm^2\, \alpha> & \cos<2\alpha>=\dfrac<1-\mathrm^2\, \alpha><1+\mathrm^2\, \alpha>\\&\\ \cos\alpha\ne 0 & \sin\alpha\ne 0\\ \hline \end\]

\(\blacktriangleright\) Формула вспомогательного аргумента: \[\begin <|c|>\hline \text<Частный случай>\\ \hline \\ \sin\alpha\pm \cos\alpha=\sqrt2\cdot \sin<\left(\alpha\pm \dfrac<\pi>4\right)>\\\\ \sqrt3\sin\alpha\pm \cos\alpha=2\sin<\left(\alpha\pm \dfrac<\pi>6\right)>\\\\ \sin\alpha\pm \sqrt3\cos\alpha=2\sin<\left(x\pm \dfrac<\pi>3\right)>\\\\ \hline \text<Общий случай>\\ \hline\\ a\sin\alpha\pm b\cos\alpha=\sqrt\cdot \sin<(\alpha\pm \phi)>, \ \ \cos\phi=\dfrac a<\sqrt>, \ \sin\phi=\dfrac b<\sqrt>\\\\ \hline \end\]

Зная идею вывода формул, вы можете запомнить лишь несколько из них. Тогда остальные формулы вы всегда сможете быстро вывести.

Вывод всех основных тождеств был рассказан в предыдущем разделе “Введение в тригонометрию”.

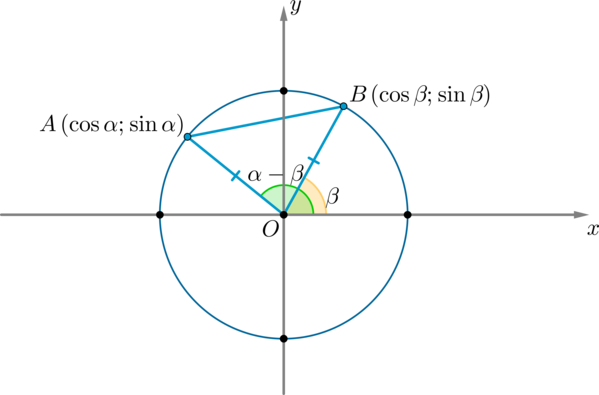
\(AB^2=AO^2+BO^2-2AO\cdot BO\cdot \cos(\alpha-\beta)=1+1-2\cos(\alpha-\beta) \ (1)\) (т.к. \(AO=BO=R\) – радиус окружности)

По формуле расстояния между двумя точками на плоскости:

Таким образом, сравнивая равенства \((1)\) и \((2)\) :

Отсюда и получается наша формула.

\(\blacktriangleright\) Вывод остальных формул суммы/разности углов:

Остальные формулы с легкостью выводятся с помощью предыдущей формулы, свойств четности/нечетности косинуса/синуса и формул приведения \(\sin x=\cos(90^\circ-x)\) и \(\cos x=\sin (90^\circ-x)\) :

\(\blacktriangleright\) Вывод формул двойного и тройного углов:

Данные формулы выводятся с помощью предыдущих формул:

1) \(\sin 2\alpha=\sin(\alpha+\alpha)=\sin\alpha\cos\alpha+\sin\alpha\cos\alpha=2\sin\alpha\cos\alpha\)

разделим числитель и знаменатель дроби на \(\cos^2\alpha\ne 0\) (при \(\cos\alpha=0 \Rightarrow \mathrm\,2\alpha=0\) ):

5) \(\sin3\alpha=\sin(\alpha+2\alpha)=\sin\alpha\cos2\alpha+\cos\alpha\sin2\alpha=\sin\alpha(1-2\sin^2\alpha)+\cos\alpha\cdot 2\sin\alpha\cos\alpha=\)

6) Аналогично выводится, что \(\cos3\alpha=\cos(\alpha+2\alpha)=4\cos^3\alpha-3\cos\alpha\)

\(\blacktriangleright\) Вывод формул понижения степени:

Данные формулы — просто по-другому записанные формулы двойного угла для косинуса:

1) \(\cos2\alpha=2\cos^2\alpha-1 \Rightarrow \cos^2\alpha=\dfrac<1+\cos2\alpha>2\)

2) \(\cos2\alpha=1-2\sin^2\alpha \Rightarrow \sin^2\alpha=\dfrac<1-\cos2\alpha>2\)

\(\blacktriangleright\) Вывод формул произведения функций:

1) Сложим формулы косинуса суммы и косинуса разности двух углов:

Получим: \(\cos(\alpha+\beta)+\cos(\alpha-\beta)=2\cos\alpha\cos\beta \Rightarrow \cos\alpha\cos\beta=\dfrac12\Big(\cos(\alpha-\beta)+\cos(\alpha+\beta)\Big)\)

2) Если вычесть из формулы косинуса суммы косинус разности, то получим:

3) Сложим формулы синуса суммы и синуса разности двух углов:

\(\blacktriangleright\) Вывод формул суммы/разности функций:

Получили формулу суммы косинусов.

Получили формулу разности косинусов.

Получили формулу суммы синусов.

4) Формулу разности синусов можно вывести из формулы суммы синусов:

Аналогично выводится формула суммы котангенсов.

\(\blacktriangleright\) Вывод формул выражения синуса и косинуса через тангенс половинного угла:

(разделим числитель и знаменатель дроби на \(\cos^2\alpha\ne 0\) (при \(\cos\alpha=0\) и \(\sin2\alpha=0\) ):)

\(\blacktriangleright\) Вывод формул вспомогательного угла:

Данные формулы выводятся с помощью формул синуса/косинуса суммы/разности углов.

\(a\sin x+b\cos x=\sqrt\left(\dfrac a<\sqrt>\sin x+ \dfrac b<\sqrt>\cos x \right)=\sqrt\big(a_1\sin x+b_1\cos x\big)\)

\(\sqrt\,\big(\cos \phi \sin x+\sin \phi\cos x\big)=\sqrt\,\sin (x+\phi)\) (по формуле синуса суммы двух углов)

Значит, формула выглядит следующим образом: \[<\large\,\sin (x+\phi),>> \quad \text <где >\cos \phi=\dfrac a<\sqrt>\] Заметим, что мы могли бы, например, принять за \(\cos \phi=b_1, \ \sin \phi=a_1\) и тогда формула выглядела бы как \[a\sin x+b\cos x=\sqrt\,\cos (x-\phi)\]

\(\blacktriangleright\) Рассмотрим некоторые частные случаи формул вспомогательного угла:

\(a) \ \sin x\pm\cos x=\sqrt2\,\left(\dfrac1<\sqrt2>\sin x\pm\dfrac1<\sqrt2>\cos x\right)=\sqrt2\, \sin \left(x\pm\dfrac<\pi>4\right)\)

\(b) \ \sqrt3\sin x\pm\cos x=2\left(\dfrac<\sqrt3>2\sin x\pm \dfrac12\cos x\right)=2\, \sin \left(x\pm\dfrac<\pi>6\right)\)

\(c) \ \sin x\pm\sqrt3\cos x=2\left(\dfrac12\sin x\pm\dfrac<\sqrt3>2\cos x\right)=2\,\sin\left(x\pm\dfrac<\pi>3\right)\)

Источник