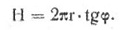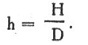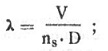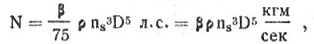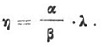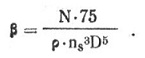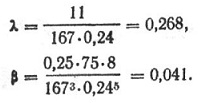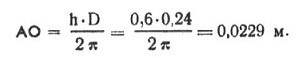Что такое шаг воздушного винта

Шаг винта

Шагом воздушного винта Н называется расстояние, на которое он поступательно продвигается за один оборот (рис. 82).

Рис. 82. Шаг винта Н

Шаг для всех частей и сечений винта одинаков, т. е. винт имеет постоянный шаг. Это графически изображено на рис. 83,а, где показаны углы установки сечений лопасти на различных ее радиусах для винта постоянного шага.

Рис. 83. Углы установки сечений лопасти на различных радиусах:
а — винт постоянного шага; б — винт переменного шага

В действительности же условия работы винта в податливой среде (воздух) более сложны и форма винтовой поверхности, которой придерживались ранее, невыгодна. В настоящее время винты строятся переменного вдоль лопасти шага (рис. 83,6), который возрастает к концу лопасти. К винтам переменного шага также применяется понятие «шаг винта», но условно берется шаг, соответствующий сечению, расположенному на 0,75 R (или 75%).

Геометрический шаг винта Я можно подсчитать по формуле:

где R — радиус винта до рассматриваемого сечения допасти;
ϕ — угол установки профиля дужки лопасти в данном сечении.

Вследствие податливости воздуха винт в действительности за один оборот продвигается на расстояние меньше, чем H. Это расстояние называется поступью винта H и определяется из выражения:

аде v — (поступательная скорость винта, м/сек; n — число оборотов винта в секунду.

Разность между геометрическим шагом и поступью называется скольжением винта
S = H—Hа.

Для характеристики кривизны лопасти, или крутки лопасти, необходимо определить угол наклона всех сечений лопасти относительно одного из них. Разность между углами наклона сечений у конца лопасти и у комля называют закруткой лопасти.

Мощность винта данного диаметра, точнее, способность винта к поглощению мощности зависит от угла установки лопастей и от их площади. Последняя величина дается в виде отношения суммарной площади всех лопастей винта к площади, ометаемой винтом, и называется перекрытием винта.

С учетом скольжения геометрический, шаг винта может быть подсчитан из выражения:

где v — поступательная скорость винта, задаваемая конструктором; n — число оборотов винта, зависящее от тина двигателя и выбранного конструктором соотношения чисел оборотов коленчатого вала двигателя и винта; S — скольжение винта, которое выражается процентах от геометрического шага и для расчета аэросанных винтов принимается равным 25—30%.

Полученные результаты можно проверить, подсчитав углы ϕ установки сечений по лопасти, имеющие прямую зависимость от шага винта.

На рис. 84 показаны кривые углов установки сечений лопасти по отношению к относительному радиусу винта для уже построенных и испытанных аэросанных воздушных винтов, а в табл. 10 указаны основные данные этих винтов.

Таблица 10

№ кривой на рис. 84	Двигатель	Мощность двигателя, л. с.	Диаметр винта, м	Число оборотов винта в минуту	Аэросани
1	М-72	20	2,2	1700	РФ-12
2	НАМИ	22	1,45	2500	ОСГА-4
3	—	12	1,3	2400	ОСГА-4
4	ГАЗ-А	40	2,2	1600	А-2
5	ИЖ-49	11	1,6	1440	—
6	ГАЗ М-1	50	2	—	КМ-5
7	«Вальтер» (самолетный)	—	2,35	1400	—

Рис. 84. Кривые углов ϕ установки сечений лопасти, по отношению к относительному радиусу винта для аэросанных воздушных винтов

Источник

Шаг винта

Шаг винта — одна из основных технических характеристик воздушного или гребного винта, зависящая от угла атаки его лопастей при их круговом движении в газовой или жидкостной среде.

Шаг винта — расстояние, пройденное поступательно винтом, ввинчивающимся в твердую среду, за один полный оборот (360°). Находится в тангенциальной зависимости от угла наклона лопастей относительно плоскости, перпендикулярной оси винта. Измеряется в единицах расстояния за один оборот. Чем больше шаг винта, тем больший объём газа или жидкости захватывают лопасти, однако, вследствие увеличения противодействия, тем больше нагрузка на двигатель и меньше скорость вращения винта (обороты). Конструкция современных воздушных и гребных винтов предусматривает способность изменения наклона лопастей без остановки агрегата.

Содержание

Воздушный винт (пропеллер)

В самолёте с винтовым движителем управление шагом винта осуществляется экипажем. Для самолёта шаг винта функционально является аналогом коробки передач в автомобиле. Увеличение шага приводит к увеличению тяги винта, уменьшение шага винта уменьшает тягу. Однако, при маленькой скорости движения и большом шаге винта (близком к 85° относительно плоскости винта) на лопастях будет формироваться срыв потока, и скорость движения будет увеличиваться очень медленно, так как лопасти будут просто перемешивать воздух, создавая очень маленькую тягу. Напротив, в случае маленького шага (5° — 10°) и высокой скорости полёта лопасти будут захватывать малый объём воздуха, скорость воздушного потока, создаваемого винтом, будет приближаться к скорости движения набегающего воздуха, остатки которого будут врезаться в винт и тормозить полёт. В некоторых случаях лопасти просто не выдержат перегрузок и разрушатся.

В связи с этим, пилотам (в особенности, времён Второй мировой войны) приходилось постоянно следить за скоростью, шагом винта и оборотами двигателя. Умело манипулируя оборотами и шагом винта, в зависимости от скорости полёта, можно было добиться меньших оборотов двигателя при высокой скорости, причём скорость не падала, а даже увеличивалась. Чтобы снизить расход топлива, а также не утруждать двигатель сильнейшими нагрузками, приходилось искать золотую середину.

На относительно современных турбовинтовых двигателях самолётов и вертолётов установлена автоматика, поддерживающая частоту вращения воздушного винта постоянной, за счёт непрерывной корректировки угла установки лопастей винта, а значит, и нагрузки на двигатель. Изменение мощности двигателя в сторону уменьшения или увеличения путем изменения подачи количества топлива приводит к автоматическому соответствующему изменению шага при сохранении неизменной частоты вращения. Говорят, что винт с большим шагом загружен, а с малым шагом — облегчён.

При аварийной остановке двигателя в полёте для снижения лобового сопротивления устанавливают максимальный угол наклона лопастей, равный 90° (параллельно оси винта). Значение шага винта в этом случае теряет смысл и становится условно равно ∞. Такой винт называется зафлюгированным.

На некоторых самолётах реализована система реверса тяги с помощью изменения шага винта, когда при приземлении во время пробега устанавливают отрицательный угол наклона лопастей, таким образом, вектор тяги винта меняет направление на обратное. Впрочем, сопротивление потоку незафлюгированного воздушного винта настолько велико, что на многих турбовинтовых самолётах для эффективного торможения в полёте или при пробеге на посадке вполне достаточно установить малый шаг винта (облегчить винт) простым переводом рычага управления тягой двигателя на минимальную тягу.

Несущий винт вертолета

Ветрогенератор

Управление шагом винта в промышленных ветряных турбинах позволяет достичь большей эффективности генератора.

Источник

Как вычислить шаг воздушного винта

Чтобы обеспечить поступательное движение модели самолета, необходимо приложить к ней силу тяги. Ее создает воздушный винт, приводимый во вращение авиамодельным двигателем. Лопасти винта, вращаясь, отбрасывают поток воздуха назад — в сторону, противоположную направлению полета. Чем больше масса и скорость воздушного потока, отбрасываемого винтом, тем больше сила тяги винта.

Воздушные винты имеют различные геометрические характеристики. Важнейшими из них являются диаметр и шаг винта.

Диаметр винта D_B — это диаметр окружности, описываемой при вращении концами лопастей.

Теоретический шаг винта Н — это расстояние, проходимое элементом лопасти в направлении полета за 1 оборот винта, движущегося поступательно с определенной скоростью; при этом предполагается, что винт вращается в неподатливой (твердой) среде (см.рис). Но так как винт вращается в воздухе, частицы которого проскальзывают на поверхности винта, та за 1 оборот он проходит меньшее расстояние. Фактически пройденное расстояние называется действительным шагом или поступью винта, а разница между теоретическим (расчетным) шагом и действительным — скольжением. Действительный шаг винта можно вычислить по формуле H=v/n,

где v — скорость модели, м/с;

Для сравнения различных винтов введено понятие относительного шага: h=H/D_B у кордовых пилотажных моделей относительный шаг воздушных винтов равен (0,4—0,6) D_B. Для получения полной мощности двигателя модели нужно правильно подобрать размеры винта — диаметр, шаг, ширину лопасти.

Рассмотрим упрощенный способ расчета воздушного винта для кордовой тренировочной модели с двигателем МАРЗ-2,5: скорость полета 80 км/ч (22 м/с), частота вращения винта 10 000 об/мин (166 с-1).

Более детально ознакомиться со способами расчета воздушного винта можно в замечательной книге Жидкова Станислава «Секреты высоких скоростей кордовых моделей самолетов» начиная с 113 страницы

Если вам нужны простые советы и рекомендации по выбору воздушного винта для своей модели, смотрите тут.

Воздушный винт дополнительные сведения.

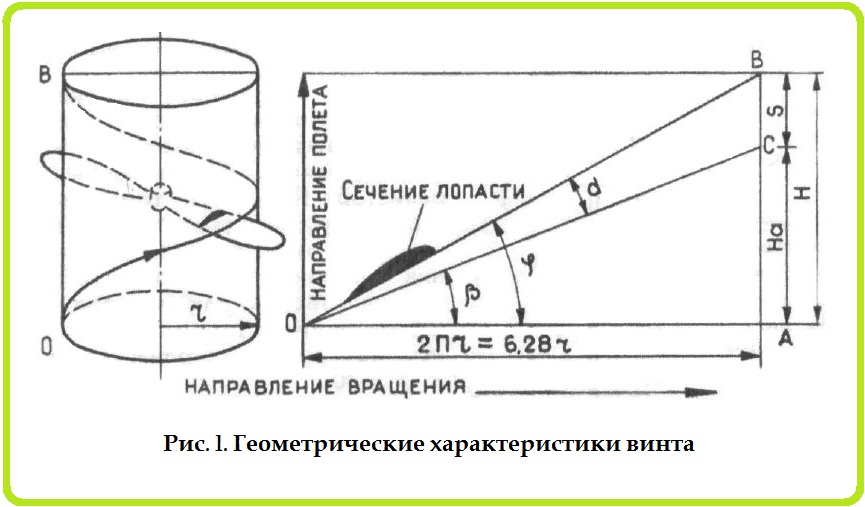
Рис. 1. Геометрические характеристики воздушного винта

Основные геометрические характеристики винта — его диаметр D и шаг — Н.

Если предположить, что винт вращается в плотной неупругой среде и вокруг оси винта описать цилиндр произвольного радиуса — r, то сечение лопасти, лежащее на поверхности этого цилиндра будет двигаться по винтовой линии (рис. 1) с углом подъема (углом установки) —ϕ. В развертке винтовая линия изобразится диагональю — ОВ, а сторона АВ характеризует перемещение сечения лопасти за один оборот, то есть шаг винта Н. Его можно выразить формулой:

Зная угол установки каждого сечения лопасти и радиус — r, можно найти соответствующий шаг. Если все сечения лопасти винта имеют одинаковую величину Н, то такие винты называются винтами постоянного шага; у винтов переменного шага в различных сечениях лопасти значения Н различны. Изменение шага по длине лопасти зависит от конструкции и формы винта. Обычно шаг винта к концу лопасти уменьшают.

Относительный шаг — это отношение шага к диаметру

Поскольку лопасть винта движется в упругой среде — воздухе, то за один оборот винт проходит расстояние меньше теоретического шага, именуемое поступью винта — Н_а (рис. 1).

Разность между шагом винта и его поступью называется скольжением — S = H—Н_а (рис. 1). Скольжение обычно дается в процентах. Для таймерных моделей с компрессионными силовыми установками оно составляет 20—40% от Н.

Из сказанного следует, что лопасть фактически движется по линии ОС, а это значит, что она имеет угол атаки α=ϕ-ß. Из рис. 1 хорошо видно, что угол атаки тем больше, чем больше скольжение S.

В расчетах часто пользуются понятием относительной поступи винта, определяемой как отношение поступи Н_а к диаметру D.

Легко показать, что

где ns — число оборотов пинта в секунду,

D — диаметр винта,

V — скорость полета модели.

Тяга, развиваемая винтом, подсчитывается по формуле: P=αρD 4 n_s 2 кг, где α— коэффициент тяги винта, который зависит от формы лопасти, h и λ; ρ — плотность воздуха.

А вот формула для мощности, необходимой для вращения винта:

где ß— коэффициент мощности винта, зависящий от тех же параметров, что и α. Коэффициентом полезного действия винта называется отношение полезной мощности, равной Р*V, к мощности, необходимой для его вращения.

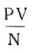
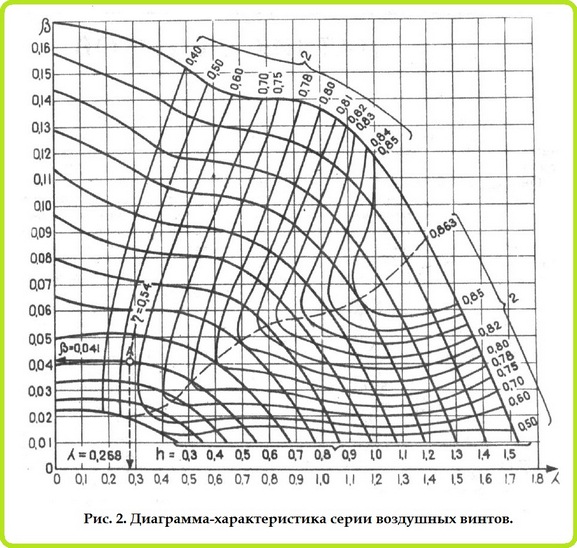
Из соотношения — получим выражение для определения коэффициента полезного действия:

Основные параметры, характеризующие работу винта, узнаем опытным путем. Проверяя винт при различных значениях λ, можно вычислить коэффициенты α и ß. Их наносят на диаграмму, называемую характеристикой винта. Исследования производятся для винтов, имеющих одинаковую форму лопастей, диаметр и профили сечений, но разный относительный шаг. Получаются характеристики серии винтов, сходных по своим формам, но имеющих различные шаги. Характеристику строят в виде группы кривых ß по λ при различных h (рис. 2).

Рис. 2. Диаграмма-характеристика серии воздушных винтов.

Зная (мощность двигателя и соответствующее ей число оборотов, а также задавшись скоростью полета модели, можно найти необходимый шаг и диаметр винта.

Пусть N = 0,25 л. с. при n_s = 167 об/сек ( 10000 об/мин), а V = 11 м/сек (около 40 (км/час). Имеется в виду таймерная модель с серийным компрессионным двигателем, скорость которой на траектории редко превышает 10—12 м/сек при диаметре винта 220—240 мм. Из формулы для определения мощности двигателя находим величину потребного ß и λ;

Если ρ=1,8, а D=0,24 м, то подставляя данные в формулы, найдем λ и ß.

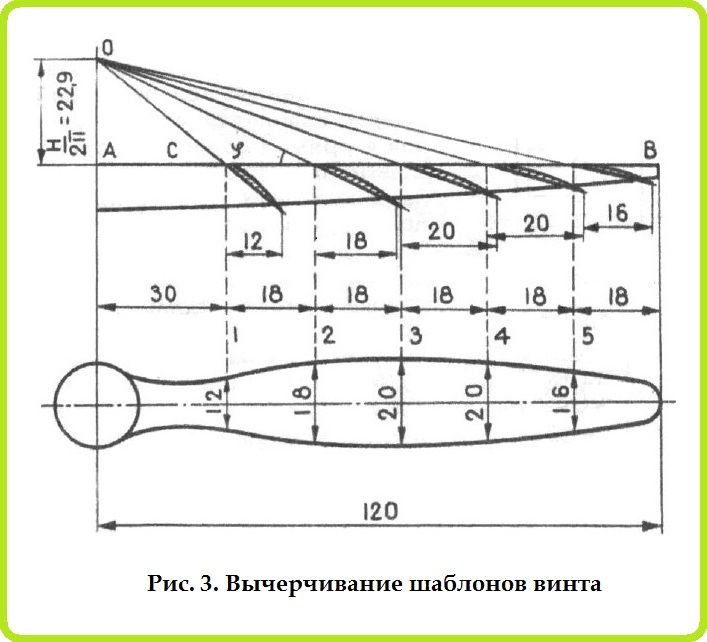
На рис. 3, откладывая по осям координат значения ß и λ, находим точку А и читаем относительный шаг h и к. п. д.—η.

Рис. 3. Вычерчивание шаблонов винта.

В нашем примере h=0,6, а η = 0,54. Тогда шаг винта будет Н = h * D = 0,6* 0,24 = 0,144 м. Для винта вычерчивают шаблоны: сначала лопасть «вид сверху», на котором размечают пять сечений (рис. 3). Таким образом узнаем верхний шаблон. Параллельно оси лопасти проводят прямую АВ, перпендикулярно к ней откладывают отрезок

После этого сечения лопасти переносят на линию АВ, полученные точки соединяют с вершиной О. Эти линии дают нам углы установки сечений. Затем ширину лопасти в первом сечении (на рис. 4—12 мм) переносят на горизонтальную прямую. Из точки С восстанавливают перпендикуляр и в пересечении с наклонной линией получают точку С’. Отрезок СС’ и есть высота бокового шаблона в сечении № 1. Дальнейшее построение видно из рисунка. Полученные точки соединяют плавной линией и получают боковой шаблон лопасти.

Значительное влияние на работу винта оказывает форма лопасти в поперечном сечении (профиль). Наибольшего значения тяга достигает при расположении максимальной толщины профиля на 30% от передней кромки.

На характеристику винта влияет и форма лопасти в плане. От взаимного расположения оси продольной жесткости лопасти и точки приложения полной аэродинамической силы образуется момент, который скручивает лопасть, увеличивая или уменьшая шаг.

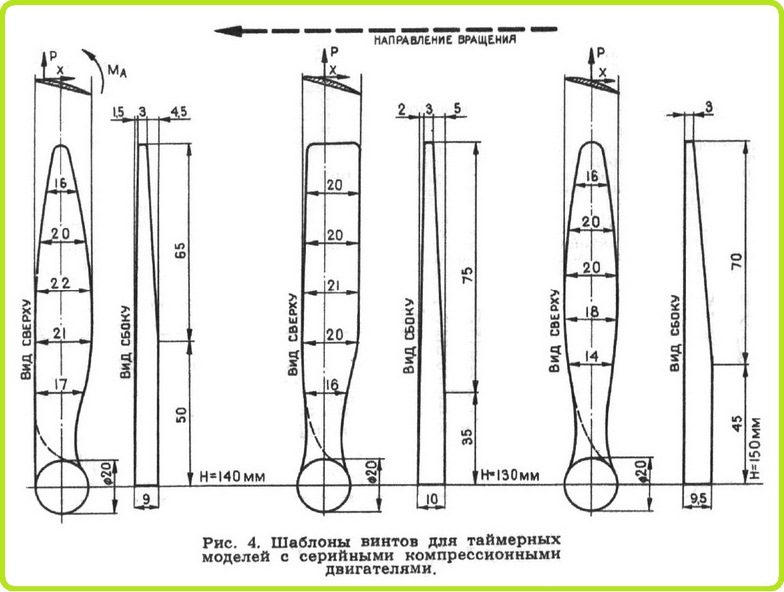
На рис. 4 показаны шаблоны нескольких различных винтов.

Источник

Воздушные винты-ликбез

воздушные винты——автор Книжников ВВ

воздушный винт открытого типа называется пропеллер

Равномерная крутка лопасти обеспечивает постоянный геометрический шаг винта для прямого набегающего потока! В первую очередь они делятся на так называемые тяговые и скоростные——принято считать, что если шаг винта H меньше диаметра D или соотношение шага к диаметру меньше единицы К=H/D, где ещё не начался полный срыв потока с лопастей из-за угла атаки менее 12 градусов, то это тяговый пропеллер с относительно большой стендовой удельной тягой!

для мультикоптеров К=0.25 или 1/4 называют условно четвертной——

К=0.33 или 1/3 треугольный—-

К=0.5 или 1/2 половинный—-

и для самолетов К=0.62 или золотого сечения по тяге—-

для медленных водоотталкивающих судов гребные винты К=0.9-1.1——

Авиамодельных винты условно принято называть коптерными для относительного шага 0.3-0.5 с вогнутовыпуклым профилем лопастей с кривизной 5-8% и самолётными при H/D= 0.6-1.1с плосковыпуклым профилем толщиной 10-16%!

Соотношение геометрического шага Н к диаметру D воздушного винта определят кпд как соотношение приращенной мощности потока к механической мощности на валу мотора в разных режимах полёта—

1)для висючек типа мультироторных платформ Н/D=0.24 получается максимальная удельная тяга для тяжелых аппаратов!

4)Н/D =1 или квадратный винт хорош для скоростного боевого пилотажа и высокого крейсера

5)Н/D=1.62 для пиковых максимальных скоростей типа гонки, для гребных винтов и низкоскоростных импеллеров,

6)Н/D=2.6 уже для больших скоростей у вв на высоте и импеллеров средней скорости,

7)Н/D=4.2 для импеллеров околозвуковых скоростей

форма и удлинение лопастей авиамодельных винтов

1) исторически эллипсоидная форма лопасти называется русским винтом при Куд=5-6 обычно слоуфлаеры из термопластика,

2) прямоугольная при Куд=7-8 обычно для двс из реактопластика с толстой комлей лопастей,

3) трапецивидная с сужением 2.5-3 и Куд=9-10 типа диджиай стиль и т-моторс,

4) типа китового плавника сложной современной формы Куд=6-8 типа граупнер и аэронавт стиль,

5) оригинальной гибридной формы с сужением 2-2.5 и Куд=7-10 типа апс стиль,

6) усеченный овал с Куд=6-7 скоростные высокооборотные деревянные или пластмассовые,

7) оригинальный винт Книжникова ВВ сложной формы с удлинением лопастей 6-7.

кпд винта от габаритов

КПД пропульсивной системы полёта в целом(внешний кпд)— это соотношение поглащенной мощности планером к мех. мощности на валу!

На практике начальный кпд или Кво воздушных винтов в большой авиации 0.99 или 99% обусловлен огромными габаритами диаметром 6-8 метров,много лопастностью 4-8штук, узкими с большим удлинением лопастями и большим числом Рейнольдса более двух миллионов, низким профильным сопротивлением, малой шероховатостью и низкой частотой вращения 660-780 об/мин и большим относительным шагом, как соотношение шага к диаметру 2.5-3 раза и в полёте имеет полный кпд около 95% при горизонтальной скорости полёта 700-900 км в час!

В средней авиации кпд в полёте около 90% при РЕ=1000 000, так как меньше габариты диаметром 4-5 и больше частота вращения 900-1000 при скоростях 500-600 км в час!

в малой реальный кпд=85% не более при оборотах 1500-1800, диаметр 2-3 метра при скорости 300-400 км вчас!

на бпла и ультролайтах кпд =75% при винтах 1-1.3 метра и частотой 3600-4200 150-180 км в час!

летающие игрушки кпд=50% при д=0.1-0.13м—-13 000-16 000 при 40-45 км/ч

так как число РЕ для лопастей не более 40 000—- вязкое, липкое обтекание!

то есть летать на низком крейсере на моторе невыгодно,проще выключить вмг и перейти на планирование в динаме или парение в термиках

частота вращения винта ограничена окружной скоростью кончиков лопастей и не должна превышать скорость звука из-за волнового кризиса, но на практике не более 270 м/с для ла!

относительное скольжение винта и угол атаки

Приведенный угол атаки лопасти условно считается на сечении 0.75 радиуса—-но на самом деле угол атаки минимален на кончике и максимален в комле, но это компенсируется изменением формы профиля и ширины лопасти для более равномерного распределения силы тяги и момента аэродинамического сопротивления по длине лопасти!

Разница между геометрическим шагом Н и поступью h задаёт скольжение! Так как угол атаки лопасти к набегающему потоку в горизонтальном полёте зависит только от относительного скольжения Кскол=(Н-h)/Н=1-Купор, а само скольжение зависит от режима полёта или потребной тяги то получается, что для квадратного винта

При пикировании в 30гр винт полностью разгружен и скольжение равно нулю и угол атаки нулевой и нет тяги—вырождение при полном газе

1) при пологом снижениив 5-10гр скольжение минимально 0.05-0.07 и угол атаки всего 1-1.5 гр,

2) на максим скорости горизонтального полета скольжение уже 0.1 и угол атаки 2 градусов!

3) при полёте в пологую горку 20-30 гр возвышения или мягком вираже скольжение 0.2-0.25 и угол атаки 4-5 гр пол-тяги от стопа,

4) при полёте в 40-50 гр возвышения или среднем вираже скольжение 0.3-0.35 и угол атаки 6-7гр,

5) при крутой горке в 60 гр или крутом вираже скольжение 0.4 и угол атаки 8 гр,

6) при вертикальном полёте вверх скольжение 0.45 и угол атаки 10 гр,

все самолётные винты сильно разружают мотор на полном газу по моменту сопротивления при прямолинейном горизонтальном полёте ла в 1.1-1.7 раз относительно режима на стопе и соответственно пропорционально падает потребляемая мощность и ток для эму—-и как следствие падает текущая сила тяги от винта в полёте на максимальной горизонтальной воздушной скорости до запирания силой общего аэродинамического сопротивления планера бпла.

Вв является адаптивным движителем в зоне рабочих углов атаки лопасти в набегающем потоке в диапозоне 1-12гр—-то есть при выполнении силовых фигур типа вираж, петля, где образуется перегрузка или горка с повышением тяги, пропеллер сам нагружает мотор мощностью с ростом от относительного скольжения и падения скорости полёта при полном газу! Это хорошо слышно по изменению частота вращения винта и тону воя от режима полета во время высшего пилотажа.

режим полета и эффективность пропеллера

Так как тяга винта для самолётов не играет существенной роли от стопа до скорости сваливания, то шаг подбираеться так, чтобы срыв потока на лопастях пропадал именно на границе сваливания ла, называется подхват—-то есть на стопе мотор немного перегружен по моменту сопротивления при винте фиксированного шага или вфш, чем выше нагрузка на крыло тем больше скорость сваливания и крейсер!

И поэтому для каждого режима полета есть оптимальный относительный шаг, когда эффективность винта максимальна

1) Пик тяги рассчитанный на скорость планирования с АКмах или 1.2-1.3 скорости сваливания даёт максимальную скороподъёмность типичное соотношение шага к диаметру 0.6—0.7 при КПДв=60%-63% соответственно—режим пилотажа

2) Высокий крейсер или 1.6-2.0 скорости сваливания дает пик кпд на винте H/D = 0.8-0.9 при КПДв=65%-67%—для бпла

3) Пик скорости на гонках 1.0-1.1 шага к диаметру винта при КПДв=69%-71%—правда долго разбегаться будет при винте фиксированного шага—гонка

оптимальный диаметр винта от миделя ла

Шаг винта Ш определяет желаемую скорость полёта—— при постоянной частоте вращения! Чем меньше шаг, а значит и меньше скорость, тем больше ометаемая площадь,а значит больше тяга при той же мощности! Фактически диаметр винта (ометаемая площадь) отвечает за тягу в горку и шаг винта за скорость полёта, а произведение диаметра на шаг (геометрическая тяжесть движителя) за поглащённую мощность потока—чем больше это произведение, тем больше потребная мощность двигателя. эмпирика для авиамодельных винтов постоянная для конкретной вмг H1+D1=H2+D2 например в дюймах 8+8=7+9=6+10

оптимальный диаметр двухлопастного пропеллера для крылатого ла на двух скоростях планирования или 2.5 скоростей сваливания—-

Все производители моторов рекомендуют диаметр и шаг допустимых винтов, тогда достаточно замерить тягу безменом и частоту вращения винта тахометром прямо на модели на стопе——например винт слоуфлаер 10/4 или D=254мм и H=102мм! Проблема в том, что разные производители пропеллеров указывают разный параметр шага винта (второе значения в дюймах,первое это диаметр—-некоторые пишут максимальный шаг нулевой тяги, другие геометрический шаг,третьи поступь винта на стенде! Поэтому только практические замеры тяги и оборотов на стопе дадут истиную картину хар-ки винта.

Сила тяги авиамодельного винта на стопе на уровне моря Fст=0.9(Dhf)2,

где поступь эмпирически для двухлопастного винта с плосковыпуклым профилем лопасти типа ДВС или ЕР h=0.45D(H/D)0.5—-

с вогнутовыпуклым профилем типа слоуфлаер h=0.5D(H/D)0.5

упрощённо для двухлопастого винта Fст=0.25D3 Н f2

Полезная мощность движителя на стопе равна произведению тяги на приращенную скорость потока в плоскости винта! Pполез=Fv=Fhf

I = Fст Н Kхх— удобно для тяговых винтов коптеров ш/д=0.3—0.4

тогда сразу подбирается мотор с потребляемым током не менее 10а и соответствующий регулятор хода

Потребляемая мощность электро-вмг на стопе ( ватт) приближенно равна произведению силы тяги ( ньютон) на максимальную теоритическую скорость потока от винта ( метры в секунду) (шаг(метр) х частоту вращения под нагрузкой (обор/сек)!

1) тяга F=(UаккуIпотр)/(Нfнаг)=(10а х12в)/ (0.12м х 200гц)=120вт/24м/с=5н=500г силы

2) сила тока Iпотр= (FНfнаг)/Uакку=(10н х 0.1м х120гц)/15в=120вт/15в=8а

3) частота fнаг=(UаккуIпотр)/(FН)=(24в х15а)/(12н х 0.15м)=360вт/1.8нм=200обор/сек

4) шаг Н=(UаккуIпотр)/(fнагF)= (50в х100а)/(125гц х160н)=5000вт/20000нгц=0.25м

Для бпла типа мотопланер актуально применение в режиме планирования в термичке винтов со складывающимися по потоку лопастями состоящего из хаба, кока и лопастей!

например промышленные хабы и лопасти отлитые из термопластика—-

1) винт диаметром 305мм и шагом 230мм имеет гарантированный предел в 7000 оборотов в мин——

2) винт диаметром 280мм и шагом 205мм имеет предел в 8000 оборотов в мин——

3) винт д255мм ш180мм при 9000—

4) винт д230мм ш160мм 10 000—-

5) д200мм ш150мм 11 000—

6) д190мм ш140мм 12 000—

7) д180мм ш130мм 13 000—-

8) д170мм ш120мм 14 000—-

9) д160мм ш110мм 15 000—

10) д150мм ш100мм 16 000—

физический анализ упругости винтов Есть несколько граничных частот работы винта!

2) крутильная резонансовая частота отвечает за флаттер лопастей характеризуется воем!

3) частота вращения определяется прочностью комли лопасти на разрыв от ценробежных сил!

1) типичный относительный шаг многолопастного винта 3-4 диаметра в больших турбовинтиляторных двигателях и 1.5-2 у авиамодельных импеллерах——чем больше относительный шаг, тем больше кол-во лопастей по тождеству n=(3-5)(H/D)!

4) соотношение входной площади губы к площади среза сопла не более 2 единиц или коэффициент сужения потока 1.4- 2——а диаметр входного патрубка больше диаметра крыльчатки в 1.1-1.2 раза!

5) соотношение входного сечения импеллера к полному миделю самолёта 0.2-0.25 для реактивных полукопий!

расчёт тяги и мощи импеллеров

Для большинства импелеров с относительным шагом 1.5-2, где поступь примерно равна диаметру крыльчатки на Сулопасти( h=CyD), есть простой расчёт силы тяги (ньютон) на уровне моря равной——

например для семилопастной крыльчатки от компьютерного куллера(0.9х(0.075м)2 х 280Гц х1.6)2=5.14Н=520 грамм силы!

потребляемая электрическая мощность (ватт)——

например 5.14н х 0.075м х 280гц х 1.6= 173 вт!—-удельная тяга 520г/173вт=3г/вт.

например 5.14н х 0.075мм х 24гц/в x(1.6)0.5=11.5а!—-Uakky=Pпот/Iст=173вт/11.5а=15в

Особенности применения импеллеров для реалистического полёта—-

1)тяговооруженность на старте при полном газу не более 0.7

2)сумма площадей воздуховода (входных отверстий и щелей) не менее двух площадей сопла

3)профиль лопастей крыльчатки желательно вогнуто выпуклый

4)масса липо акку в граммах эмпирически равна мощности потребления в ваттах на стопе

5)размашистый пилотаж—-большие радиусы поворотов, петли с пикирования, угол подъёма в горку не более 30 градусов

7)коэф. перекрытия лопастей не менее 0.6

На практике тяга винта в горизонтальном полёте на полном газу меньше в 2-3 раза от тяги на стопе—-

1) падение тяги примерно в два раза у гоночных винтов (квадратные) и у импеллеров на максимальной горизонтальной скорости

2 )падение в два с половиной раза у скоростных винтов с относительным шагом Ш/Д=0.6—0.8

3) падение в три раз у тяговых винтов с Ш/Д=0.4—0.5

Источник