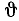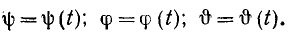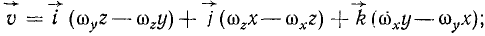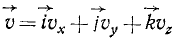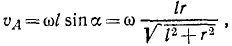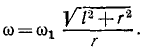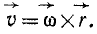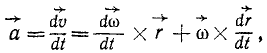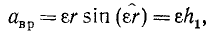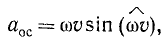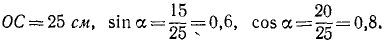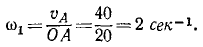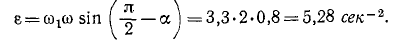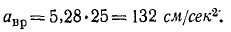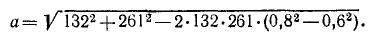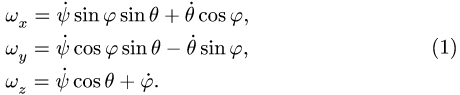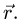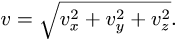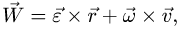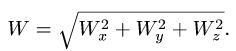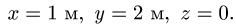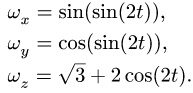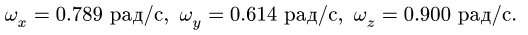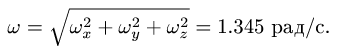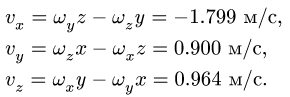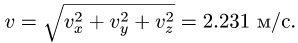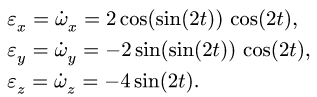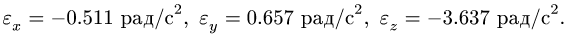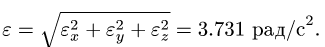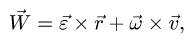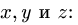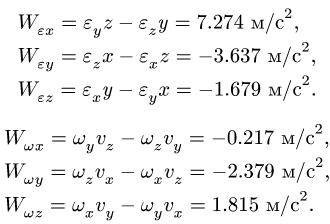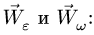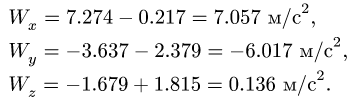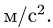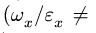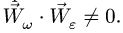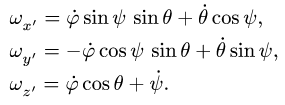что такое сферическое тело

сферическое тело

Смотреть что такое «сферическое тело» в других словарях:

Сверхмассивные черные дыры — Связать? Сверхмассивная черная дыра некогда ядро суперзвезды, ранее ядро звезды первого уровня образовавшейся после Большого Взрыва и до образования галактик, прежде ядро суперновой сжатое при звездном коллапсе взрывом звезды, остаточное… … Википедия

ТЯГОТЕНИЕ — или гравитация, свойство материи, которое состоит в том, что между любыми двумя частицами существуют силы притяжения. Тяготение универсальное взаимодействие, охватывающее всю доступную наблюдению Вселенную и потому называемое всемирным. Как мы… … Энциклопедия Кольера

Приливные силы — Стиль этой статьи неэнциклопедичен или нарушает нормы русского языка. Статью следует исправить согласно стилистическим правилам Википедии. Во … Википедия

Приливная сила — Рис. 1. Тело в поле тяготения массы (расположена справа за границами рисунка). Вверху: Силы тяготения максимальны для частей тела, ближних к тяготеющей массе и минимальны для дальних частей. Внизу: приливные силы как разность сил, действующих на… … Википедия

Приливное взаимодействие — Рис. 1. Тело в поле тяготения массы (расположена справа за границами рисунка). Вверху: Силы тяготения максимальны для частей тела, ближних к тяготеющей массе и минимальны для дальних частей. Внизу: приливные силы как разность сил, действующих на… … Википедия

Приливное воздействие — Рис. 1. Тело в поле тяготения массы (расположена справа за границами рисунка). Вверху: Силы тяготения максимальны для частей тела, ближних к тяготеющей массе и минимальны для дальних частей. Внизу: приливные силы как разность сил, действующих на… … Википедия

Приливные взаимодействия — Рис. 1. Тело в поле тяготения массы (расположена справа за границами рисунка). Вверху: Силы тяготения максимальны для частей тела, ближних к тяготеющей массе и минимальны для дальних частей. Внизу: приливные силы как разность сил, действующих на… … Википедия

СФЕРИЧЕСКИЙ — СФЕРИЧЕСКИЙ, сферическая, сферическое (мат., спец.). прил. к сфера в 1 знач.; шарообразный, шаровидный. Сферическое тело. Сферическая поверхность. Сферический аэростат. Сферический треугольник (треугольник на поверхности сферы). Сферическая… … Толковый словарь Ушакова

Циста — (от греч. κύστις пузырь) временная форма существования микроорганизмов (обычно бактерий и простейших (протистов), многих одноклеточных), характеризующаяся наличием защитной оболочки, в неблагоприятных условиях или в определенные моменты их… … Википедия

Источник

Сфера

Сфе́ра (греч. σφαῖρα — мяч) — замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, называемой центром сферы. Сфера также является телом вращения, образованным при вращении полуокружности вокруг своего диаметра. Площадь сферы в градусной мере с учётом непостоянства значения размеров дуг составляет 41252.96 кв. градусов.

Сфера является частным случаем эллипсоида, у которого все три оси (полуоси, радиусы) равны. Сфера является поверхностью шара.

Объёмы цилиндра, вписанной в него сферы, касающейся его основания, и двух конусов, имеющих общую вершину в центре основания и основания, равные основаниям цилиндра, находятся в соотношении 1:2:3 [1]

Содержание

Основные геометрические формулы

Сфера в трёхмерном пространстве

где — координаты центра сферы, — её радиус.

Параметрическое уравнение сферы с центром в точке :

где и

Геометрия на сфере

Окружность, лежащая на сфере, центр которой совпадает с центром сферы, называется большим кругом (большой окружностью) сферы. Большие круги являются геодезическими линиями на сфере; любые два из них пересекаются в двух точках.

Расстояние между двумя точками на сфере

Если даны сферические координаты двух точек, то расстояние между ними можно найти так:

Однако, если угол задан не между осью Z и вектором на точку сферы, а между этим вектором и плоскостью XY (как это принято в земных координатах, заданных широтой и долготой), то формула будет такая:

В этом случае и называются широтами, а и долготами.

n-мерная сфера

В общем случае уравнение (n-1)-мерной сферы (в n-мерном евклидовом пространстве) имеет вид:

где — центр сферы, а — радиус.

Пересечением двух n-мерных сфер является n-1-мерная сфера, лежащая на радикальной гиперплоскости этих сфер.

В n-мерном пространстве могут попарно касаться друг друга (в разных точках) не более n+1 сфер.

n-мерная инверсия переводит n-1-мерную сферу в n-1-мерную сферу или гиперплоскость.

См. также

Примечания

Полезное

Смотреть что такое «Сфера» в других словарях:

СФЕРА — (греч. sphaira шар). 1) твердое тело, в котором все точки поверхности одинаково отдалены от внутренней точки, называемой центром шар; изображение земли в виде глобуса. 2) часть пространства, в котором планета совершает свой путь. 3) в фигуральном … Словарь иностранных слов русского языка

СФЕРА — жен., греч. шар, шарообразное тело или пустота, или изображенье его на бумаге; в приложении к небесным телам: шар обращаемый на оси своей, представляющий землю нашу, или небесную твердь, с означеньем всех воображаемых кругов. Армилярная сфера,… … Толковый словарь Даля

сфера — ы, ж. sphère f. <гр. sphaira. 1. геом. Замкнутая поверхность, все точки которой одинаково удалены от одной точки (центра /. БАС 1. | перен. Сфер десять пролетев воздушных, Узрел вдали питейный дом. И. Наумов Ясон. // Ирои комич. поэма 560. 2.… … Исторический словарь галлицизмов русского языка

СФЕРА — сферы, жен. [греч. sphaira шар]. 1. То же, что шар (мат.). 2. перен. Область, место, пределы, в к рых существует, действует, развивается, применяется что н. (книжн.). «Смотря по свойству поэтического таланта и по степени его выработанности, сфера … Толковый словарь Ушакова

СФЕРА — СФЕРА, ы, жен. 1. Область, пределы распространения чего н. С. деятельности. С. влияния. 2. Среда, общественное окружение. В своей сфере. Высшие сферы (о правящих, аристократических кругах). 3. Замкнутая поверхность, все точки к рой равно удалены… … Толковый словарь Ожегова

сфера — См. область … Словарь синонимов

Сфера — (Хабаровск,Россия) Категория отеля: 3 звездочный отель Адрес: Переулок Дежнева 15, Хабаровск … Каталог отелей

-сфера — сфера компонент сложных слов, означающих: 1) одну из оболочек планет и звёзд: астеносфера атмосфера барисфера биосфера геосфера гетеросфера гидросфера гомосфера ионосфера литосфера магнитосфера мезосфера стратосфера субстратосфера… … Википедия

СФЕРА — (от греческого sphaira шар), 1) область действия, пределы распространения чего либо (например, сфера влияния). 2) Общественное окружение, среда, обстановка … Современная энциклопедия

СФЕРА — (от греч. sphaira шар) 1) область действия, пределы распространения чего либо (напр., сфера влияния).2) Общественное окружение, среда, обстановка … Большой Энциклопедический словарь

СФЕРА — замкнутая поверхность, все точки которой одинаково удалены от одной точки (центра сферы). Отрезок, соединяющий центр сферы с какой либо ее точкой (а также его длина), называется радиусом сферы. Площадь поверхности сферы S=4?R2, где R радиус сферы … Большой Энциклопедический словарь

Источник

Сферическое движение твердого тела в теоретической механике

Содержание:

Сферическое движение твердого тела:

Сферическим называют такое движение твердого тела, при котором точки тела описывают траектории, лежащие на сферах с одним и тем же неподвижным центром

Вращение тела вокруг точки

Пусть во время движения тела одна из его точек остается неподвижной. Тогда всякая другая точка тела может двигаться только по поверхности сферы, описанной вокруг неподвижной точки радиусом, равным расстоянию этой точки от неподвижной. Такое движение называют сферическим движением тела, или вращением вокруг неподвижной точки.

Положение тела, имеющего неподвижную точку, можно определить тремя независимыми углами

Углы Эйлера

Чтобы определить положение тела, имеющего неподвижную точку, построим две системы координатных осей с общим началом в этой точке О: основную xOyz и подвижную x’Oy’z’, неизменно связанную с движущимся телом (рис. 107). Три оси подвижной системы составляют 9 углов с тремя осями основной, но для определения положения тела, имеющего неподвижную точку, нет необходимости знать все 9 направляющих косинусов, так как они связаны известными из аналитической геометрии соотношениями, и независимых величин остается только три.

Положение тела, имеющего неподвижную точку, можно определить тремя независимыми углами. Эти углы обычно называют эйлеровыми.1 Ознакомимся с углами, предложенными Эйлером и применяемыми в астрономии, в гироскопии и во многих других науках.

Линией узлов называют линию ON пересечения плоскостей xОy и х’Оу’ основной и подвижной систем. Первый угол — угол прецессии ψ—лежит в плоскости хОу между неподвижной осью Ox и линией узлов. Его измеряют от оси Ox к оси ON против хода часов, если смотреть с оси Oz.

Второй—угол собственного вращения φ—лежит в плоскости х’Оу’ и его отмеривают от линии узлов до оси Ox’ против хода часовой стрелки, если смотреть с оси Oz’. Третий — угол

Во время движения тела эти углы изменяются. Чтобы задать уравнение сферического движения, надо представить их как некоторые непрерывные однозначные функции времени:

Предельное положение такой оси, вокруг которой следует повернуть твердое тело на бесконечно малый угол, чтобы перевести его из одного положения в другое, бесконечно близкое первому, называют мгновенной осью вращения

Мгновенная ось вращения

Положение тела в пространстве можно определить различными способами. В частности, для этого можно задать положение трех его точек. Применим этот способ для изучения сферического движения тела. За одну из этих точек примем неподвижную точку О (рис. 108, а), а две другие, А и В, выберем произвольно, но с условием, чтобы их скорости не были параллельны между собой.

Рассмотрим сначала точку А. Проведем прямую через точку А и неподвижную точку О. Согласно основной теореме кинематики твердого тела (77) проекции скоростей точек А и Q на АО должны быть равны. Но скорость точки О, а потому и ее проекция равны нулю. Скорость точки А нулю не равна, но проекция ее на ЛО должна равняться нулю, следовательно, скорость точки А перпендикулярна к АО. Если мы проведем через точки А и О плоскость (рис. 108, б) перпендикулярно к скорости точки А, то по той же теореме скорости точек этой плоскости должны быть перпендикулярны к прямым, соединяющим эти точки с неподвижной точкой О, т. е. перпендикулярны плоскости.

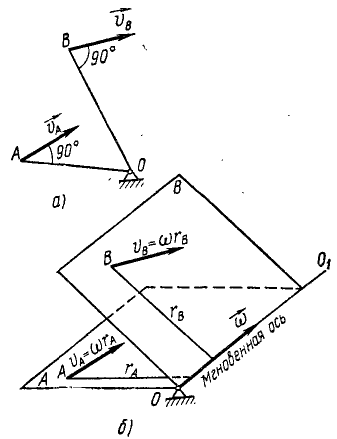
Рис. 108

Рассмотрим теперь точку В и повторим те же рассуждения. Если мы проведем через точки В и О плоскость В перпендикулярно к скорости точки В, то скорости точек этой плоскости должны быть перпендикулярны к плоскости В. Точки, лежащие на линии OO₁ пересечения плоскостей А и В, должны иметь скорости, перпендикулярные сразу к обеим пересекающимся плоскостям, что невозможно. Следовательно, скорости точек этой прямой OO₁ в данное мгновение равны нулю. Мы пришли к убеждению, что при движении тела с одной неподвижной точкой через эту точку всегда можно провести ось, скорости точек которой в данное мгновение равны нулю. Эту ось называют мгновенной осью вращения.

Если в движущемся теле существует ось, скорости точек которой в данное мгновение равны нулю, то скорости других его точек должны быть пропорциональны их расстояниям от оси. Таким образом, картина распределения скоростей в теле с одной неподвижной точкой оказалась на данное мгновение такой же, как и в теле, вращающемся вокруг неподвижной оси.

При изучении вращения тела вокруг неподвижной оси мы условились о направлении вектора угловой скорости. То же условие сохраняется на сферическое движение, где вектор угловой скорости ω направлен от неподвижной точки О по мгновенной оси вращения в такую сторону, чтобы вращение тела представлялось происходящим против хода часов, если смотреть с конца вектора ω, к точке О. Этот вектор можно переносить вдоль оси вращения, но нельзя перемещать параллельно оси. Глубокое отличие вектора угловой скорости при сферическом движении заключается в том, что он постоянно меняет свое направление.

В связи с этим другое толкование принимает и угловое ускорение. Изображая угловое ускорение тела при вращении вокруг оси вектором, мы направляли его в ту или иную сторону по вектору угловой скорости. При вращении тела относительно неподвижной точки дело обстоит иначе: направление угловой скорости меняется. Мы будем называть вектором углового ускорения тела вектор, характеризующий изменение в данное мгновение величины и направления угловой скорости тела

(97)

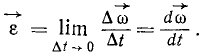
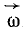
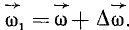
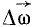
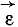
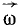
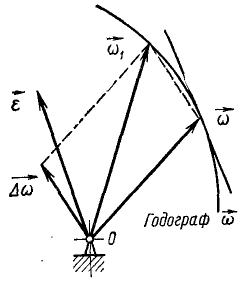
Направление этого вектора, вообще говоря, не совпадает с мгновенной осью вращения. Пусть, например, угловая скорость тела, имеющего неподвижную точку О (рис. 109) и не показанного на чертеже, в данное мгновение равна , а через малый промежуток времени Δt станет Разделив на Δt, мы получим вектор среднего углового ускорения тела. Если мы будем уменьшать промежуток времени Δt, оставляя неизменным его начало, то вектор среднего углового ускорения тела будет стремиться к своему предельному значению — вектору углового ускорения тела. Этот вектор проходит через неподвижную точку О и параллелен касательной к годографу вектора.

Рис. 109

При сферическом движении тела подвижный аксоид катится без скольжения по неподвижному

Аксоиды при сферическом движении

Положение мгновенной оси в теле, имеющем одну неподвижную точку, непрерывно меняется. Но в каждое мгновение ось имеет вполне определенное положение и всегда проходит через неподвижную точку О. Геометрическое место мгновенных осей вращения, проведенных в теле, представляет собой некоторую коническую поверхность и называется подвижным аксои-дом. Положение мгновенной оси вращения можно отметить и относительно неподвижных координат. Их геометрическое место относительно неподвижных координат, называемое неподвижным аксоидом, также является конической поверхностью с вершиной в той же неподвижной точке О. Оба конуса соприкасаются по мгновенной оси вращения. Сферическое движение тела можно представить как качение без скольжения подвижного аксоида по неподвижному.

Зависимость между проекциями скоростей точек тела, их координатами и проекциями угловой скорости выражается формулами Эйлера

Формулы Эйлера

Как было только что показано, скорость каждой точки K тела, имеющего неподвижную точку О, перпендикулярна к прямой КО и пропорциональна расстоянию KО sin α точки К от мгновенной оси вращения (рис. 110), т. е.

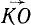
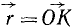
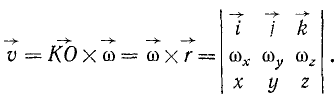
Таким образом, при сферическом движении, как и при вращательном, скорость всякой точки тела можно рассматривать как момент вектора угловой скорости тела относительно этой точки. Проведем из какой-либо точки К тела вектор в неподвижную точку О, принятую нами за начало отсчета. Этот вектор равен по модулю, но направлен противоположно радиусу-вектору точки K относительно начала отсчета О. Момент вектора угловой скорости относительно точки K представим векторным произведением и запишем в виде определителя третьего порядка, как это мы делали (см. 17 и 17′) в статике при определении момента силы:

Раскладывая этот определитель по элементам первой строки:

раскладывая скорость точки по осям координат:

и сравнивая оба равенства, мы можем выразить проекции скорости точки через проекции угловой скорости тела и координаты точки:

(98)

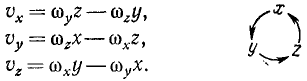
Эти соотношения, очень напоминающие знакомые нам выражения (23) момента силы относительно оси, отличаются от них не только тем, что вектор силы заменен вектором угловой скорости, но и знаками. Круговой заменой букв в любой из трех формул (98) можно получить две остальные. Эти формулы имеют применение при определении проекций скоростей точек тела, совершающего сферическое движение или вращение вокруг неподвижной оси. В частном случае, если тело вращается вокруг оси Oz, то проекции угловой скорости ω_x = ω_y = 0, a ω_z=ω, мы получаем формулы (89).

Задача №1

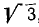
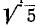
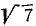
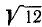
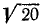
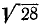
Тело движется вокруг неподвижной точки — начала координат. В некоторое мгновение угловая скорость его изображается вектором, проекции которого на координатные оси равны , , . Найти скорость точки К тела, определяемой координатами , ,.

Решение. Подставляя данные в формулы Эйлера, получим

Ответ. υ = 0. В этот момент времени мгновенная ось проходит через точки О и К.

Задача №2

Ось OA мельничного бегуна (рис. 111) вращается равномерно вокруг вертикальной оси с угловой скоростью ω₁. Длина оси OA=l, радиус бегуна равен r. Пренебрегая скольжением бегуна, определить вектор его угловой скорости.

Решение. Движение бегуна можно рассматривать как вращение около неподвижной точки О. Бегун катится без скольжения, поэтому скорость точки C соприкосновения его с горизонтальной плоскостью равна нулю, и, следовательно, в каждое мгновение ось, проходящая через точки О и С, есть мгновенная ось вращения. Центр бегуна (точка А) движется вокруг вертикальной оси, проходящей через О, с постоянной по величине скоростью

Но точка А принадлежит бегуну, а потому ее скорость в то же время является вращательной скоростью вокруг мгновенной оси вращения ОС. Опуская из А перпендикуляр на мгновенную ось, получаем

где ω—угловая скорость бегуна, а а — угол AОС. Из двух выражений υ_A находим ответ.

Ответ.

Ускорение всякой точки тела, совершающего сферическое движение, состоит из вращательного и осестремительного ускорений

Чтобы получить ускорение какой-либо точки К тела, находящегося в сферическом движении, продифференцируем по времени вектор ее скорости

(99)

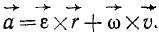
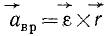
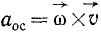
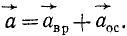
Таким образом, ускорение каждой точки К тела, имеющего одну неподвижную точку О, состоит из векторной суммы двух ускорений: вращательного ускорения и осестремительного ускорения
. В общем случае оба эти ускорения не перпендикулярны друг другу, что необходимо учесть при их суммировании (рис. 112, а).

(99 / )

Эту формулу называют формулой Ривальса.

Чтобы лучше уяснить чему равны и как направлены эти ускорения, обратимся к чертежу.

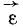
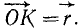
Вращательное ускорение (рис. 112, б) выражается векторным произведением углового ускорения и радиуса вектора Следовательно, оно направлено перпендикулярно плоскости, образованной этими векторами, и по модулю равно

где h₁—длина перпендикуляра, опущенного из точки К на прямую, по которой направлено угловое ускорение ε. Из формулы (100) в частности следует, что эта прямая обязательно должна проходить через неподвижную точку О, потому что в противном случае точка О имела бы неравное нулю вращательное ускорение, т. е. стала бы подвижной.

Осестремительное ускорение по модулю равно

но этот синус равен единице, так как векторы угловой и вращательной скорости взаимно перпендикулярны. Модуль же вектора вращательной скорости υ = ωh, где h—длина перпендикуляра, опущенного из точки К на мгновенную ось вращения, а потому

Направлено осестремительное ускорение перпендикулярно векторам угловой скорости тела и вращательной скорости точки К, т. е. по прямой h от точки К к мгновенной оси вращения.

Задача №3

Найти скорость и ускорение точки В конического катка, равномерно катящегося без скольжения по горизонтальной конической кольцевой опоре (рис. 113). Диаметр катка BC = 30 см, OA = 20 см, скорость центра катка υ_А = 40 см/ceκ и направлена перпендикулярно плоскости чертежа на читателя.

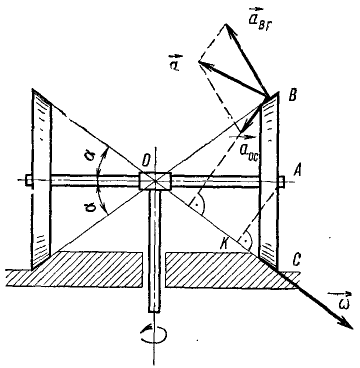
Рис. 113

Решение. Мгновенная ось проходит через неподвижную точку О и точку С, скорость которой в данное мгновение равна нулю, потому что каток катится без скольжения. Вектор угловой скорости ω направлен по мгновенной оси. Модуль его определим, разделив скорость точки А на расстояние АК от мгновенной оси. Из треугольника OAC находим OC 2 = OA 2 + АС 2 = 625. Тогда

Имея эти данные, находим угловую скорость:

Найдем теперь вектор углового ускорения. Каток катится равномерно, величина угловой скорости не изменяется, но меняется ее направление, и конец вектора угловой скорости описывает годограф—окружность радиуса ω sin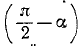. Угловая скорость ω₁, с которой поворачивается вектор угловой скорости ω, равна угловой скорости, с которой поворачивается ось OA во время движения катка:

Вектор углового ускорения равен скорости годографа вектора угловой скорости. Он направлен перпендикулярно плоскости чертежа на читателя, но приложен в неподвижной точке О:

Осестремительное ускорение по модулю равно произведению квадрата модуля угловой скорости на длину перпендикуляра h, опущенного из точки В на мгновенную ось, и направлено к оси:

α_oc = 3,3 2 ∙24 = 261 см/сек.

Угол между векторами вращательного и осестремительного ускорений равен 2α. Полное ускорение точки В определим, применив теорему косинусов

Скорость и ускорение точки тела

Постановка Задачи. Твердое тело совершает сферическое движение по закону, заданному в углах Эйлера 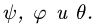Найти скорость и ускорение точки, положение которой дано относительно подвижных осей координат.

1. Воспользуемся кинематическими уравнениями Эйлера для определения проекций угловой скорости на подвижные оси координат

2. Находим проекции скорости 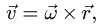на подвижные оси относительно которых задан радиус-вектор точки

3. Вычисляем модуль скорости

4. Дифференцируя по времени t проекции угловой скорости, получаем компоненты углового ускорения 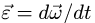в подвижных осях.

5. Ускорение точки представляем в виде векторной суммы

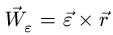
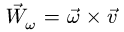
где — вращательное, a — осестремительное ускорение.

6. Находим модуль ускорения

Пример. Твердое тело совершает сферическое движение по закону, заданному в углах Эйлера 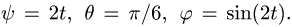При t = 1 с найти скорость и ускорение точки, положение которой относительно подвижных координат задано координатами

Углы 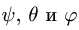даны в рад. Решение

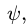
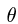
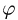
1. Зная зависимости угла прецессии угла нутации и собственного вращения от времени, воспользуемся кинематическими уравнениями Эйлера (1) для определения проекций угловой скорости на подвижные оси координат. Подставляя в (1) заданные функции, получаем

При t = 1 вычисляем

Модуль угловой скорости тела

2. Вычисляем проекции скорости точки на подвижные оси:

3. Модуль скорости точки

4. Дифференцируя пo t проекции угловой скорости, получаем компоненты углового ускорения тела в подвижных осях:

Модуль углового ускорения

5. Ускорение точки представляем в виде векторной суммы:

Гл. 10. Сферическое движение тела

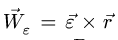
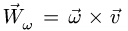
где — вращательное, a — осестремительное ускорение. Вычисляем отдельно их проекции на оси

Компоненты ускорения получаем, суммируя

6. Модуль ускорения 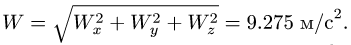Ответы занесем в таблицу. Скорости — в м/с, ускорения — в

Замечание 1. При сферическом движении тела векторы угловой скорости и углового ускорения не лежат на одной прямой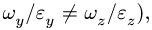а вектор осестремительного ускорения в общем случае не перпендикулярен вектору вращательного ускорения. В этом можно убедиться, вычислив скалярное произведение

Замечание 2. Кинематические уравнения Эйлера для определения проекций угловой скорости на неподвижные оси координат имеют вид

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник