что такое сети петри

Сети Петри. Структура и правила выполнения сетей Петри.

Сети Петри [ ]

Сети Петри — математический аппарат для моделирования динамических дискретных систем. Впервые описаны Карлом Петри в 1962 году.

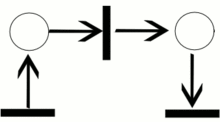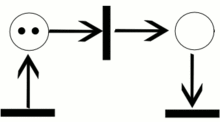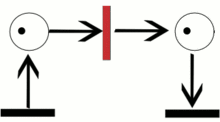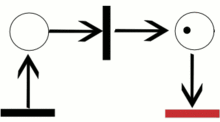
Пример работы сети Петри

Сеть Петри представляет собой двудольный ориентированный граф, состоящий из вершин двух типов — позиций и переходов, соединённых между собой дугами. Вершины одного типа не могут быть соединены непосредственно. В позициях могут размещаться метки (маркеры), способные перемещаться по сети.

Событием называют срабатывание перехода, при котором метки из входных позиций этого перехода перемещаются в выходные позиции. События происходят мгновенно, либо разновременно, при выполнении некоторых условий.

Как и стандартные UML диаграммы, BPMN и EPC, сети Петри предоставляют возможность графически иллюстрировать процессы включающие выбор, итерации и одновременное выполнение. Но в отличие от данных стандартов, у сетей Петри четкая математическая формулировка и за ними стоит развитая математическая теория.

==Структура сетей Петри==

Сеть Петри состоит из 4-х элементов:

Пример сети Петри. Белыми кружками обозначены позиции, полосками — переходы, чёрными кружками — метки.

Правила выполнения сетей Петри [ ]

Выполнением сети Петри управляют количество и распределение фишек в сети. Сеть Петри выполняется посредством запусков переходов. Переход запускается удалением фишек из его входных позиций и образованием новых фишек, помещаемых в его выходные позиции.

Переход запускается, если он разрешен. Переход называется разрешенным, если каждая из его входных позиций имеет число фишек по крайней мере равное числу дуг из позиции в переход. Фишки во входной позиции, которые разрешают переход, называются его разрешающими фишками. Например, если позиции р1 и р2 служат входами для перехода t1, тогда t1 разрешен, если р1 и р2 имеют хотя бы по одной фишке. Для перехода t3 с входным комплектом позиция р3 должна иметь не менее 3 фишек для разрешения перехода t3.

Определение. Переход маркированной сети Петри с маркировкой , разрешен, если для всех , .

Переход запускается удалением разрешающих фишек, из всех его входных позиций (количество удаленных фишек для каждой позиции соответствует числу дуг, идущих из этой позиции в переход), с последующим помещением фишек в каждую из его выходных позиций (количество помещаемых фишек в позицию соответствует количеству дуг входящих в данную позицию из перехода).

>Переход t3 I(t3) = и O(t3) = разрешен каждый раз, когда в р2 будет хотя бы одна фишка. Переход t3 запускается удалением одной фишки из позиции р2 и помещением одной фишки в позицию р3 и р4 (его выходы). Переход t4, в котором I(t4) = и O(t4) = запускается удалением по одной фишке из позиций р4 и р5, при этом одна фишка помещается в р5 и две в р6 (рис. 2).

Определение. Переход в маркированной сети Петри с маркировкой может быть запущен всякий раз, когда он разрешен. В результате запуска разрешенного перехода образуется новая маркировка :

Источник

Сети Петри

Сети Петри — математический аппарат для моделирования динамических дискретных систем. Впервые описаны Карлом Петри в 1962 году.

Сеть Петри представляет собой двудольный ориентированный граф, состоящий из вершин двух типов — позиций и переходов, соединённых между собой дугами. Вершины одного типа не могут быть соединены непосредственно. В позициях могут размещаться метки (маркеры), способные перемещаться по сети.

Событием называют срабатывание перехода, при котором метки из входных позиций этого перехода перемещаются в выходные позиции. События происходят мгновенно, либо разновременно, при выполнении некоторых условий.

Содержание

История

Виды сетей Петри

Некоторые виды сетей Петри:

Анализ сетей Петри

Основными свойствами сети Петри являются:

В основе исследования перечисленных свойств лежит анализ достижимости.

См. также

Примечания

Ссылки

Полезное

Смотреть что такое «Сети Петри» в других словарях:

Раскрашенные сети Петри — Методология создания динамической модели бизнес процесса, позволяющая проанализировать зависящие от времени характеристики выполнения процесса и распределение ресурсов для входящих потоков различной структуры. [http://www.morepc.ru/dict/]… … Справочник технического переводчика

Петри, Карл Адам — Карл Адам Петри Carl Adam Petri Дата рождения … Википедия

Петри — Фамилия Известные носители: Петри, Бернгард Эдуардович российский и советский антрополог, археолог. Петри, Генри Вильгельм нидерландский скрипач. Петри, Дональд американский киноактёр и кинорежиссёр. Петри, Лаурентиус … … Википедия

Сети — Сети: Сети I египетский фараон Сети II египетский фараон теория графов и теория сетей эти названия используются для одного математического понятия SETI (программа поиска внеземных цивилизаций) «Сети» музыкальная группа. «Сети» книга стихов… … Википедия

СЕТИ — теория графов и теория сетей эти названия используются для одного математического понятия SETI (программа поиска внеземных цивилизаций) «Сети» музыкальная группа. «Сети» книга стихов Михаила Кузмина. передачи данных I II Сети SOHO Инженерные… … Википедия

Сети I — В Википедии есть статьи о других людях с именем Сети. Сети I XIX династия Новое царство … Википедия

ПЕТРИ СЕТЬ — математическая модель дискретных динамич. систем, в том числе информационных систем (параллельных программ, операционных систем, ЭВМ и их устройств, сетей ЭВМ), ориентированная на качественный анализ и синтез таких систем (обнаружение блокировок … Математическая энциклопедия

WF-сети — WF сети подкласс сетей Петри, называемый также сетями потоков работ. Формализм WF сетей введён Вил ван дер Аальстом (англ. Wil van der Aalst) для моделирования потоков работ в workflow системах. Сеть Петри PN = (P,T,F) называется сетью … Википедия

Асинхронная логика — Содержание 1 Принцип самосинхронности 2 Краткая история … Википедия

Модель акторов — В компьютерных науках модель акторов представляет собой математическую модель параллельных вычислений, которая трактует понятие «актор» как универсальный примитив параллельного численного расчёта: в ответ на сообщения, которые он получает, актор… … Википедия

Источник

Сети Петри для моделирования

Сети Петри были разработаны и используются в основном для моделирования. С их помощью могут быть промоделированы многие системы, в особенности системы с независимыми компонентами, например аппаратное и программное обеспечение ЭВМ, физические системы, социальные и др. Сети Петри применяются для моделирования возникновения различных событий в системе. В частности, сети Петри могут моделировать поток информации или другие ресурсы системы.

В этой главе мы приведем примеры систем, моделируемых при помощи сетей Петри. Эти примеры дадут представление о большом классе систем, которые можно моделировать сетями Петри, об использующемся методе моделирования и о свойствах, которыми должны обладать моделируемые системы.

Примитивные и непримитивные события

Различают 2 вида событий:

(Иногда это обосновывается тем, что время — это непрерывная действительная переменная. Следовательно, если мы присвоим каждому событию время возникновения, то вероятность того, что любые две произвольно выбранные непрерывные действительные переменные совпадают, равна нулю, и, следовательно, события неодновременны.)

Петри и другие предложили представлять непримитивные события в сети Петри в ви-де прямоугольника

примитивные события — планками, как мы делали это раньше (как обычно).

Конфликт

Другая ситуация, в которой одновременное выполнение затруднено и которая характеризуется невозможностью одновременного возникновения событий, показана на рис. 3.8. Здесь два разрешенных перехода находятся в конфликте. Может быть запущен только один переход, так как при запуске он удаляет фишку из общего входа и запрещает другой переход.

36. Модель сети Петри для обедающих философов

Задача об обедающих мудрецах была предложена Дейкстрой и связана с пятью мудрецами, которые попеременно то думали, то ели. Мудрецы сидят за большим круглым столом, на котором много блюд китайской кухни. Между соседями лежит одна палочка для еды. Однако для приема китайской пищи необходимо две палочки, следовательно, каждый мудрец должен взять палочку слева и палочку справа: проблема, конечно, заключается в том, что если все мудрецы возьмут палочки слева и затем будут ждать, когда освободятся палочки с правой стороны, то они будут ждать вечно и умрут от голода (состояние тупика).

37. Модель сети Петри для читателей-писателей

Существует несколько вариантов задачи о чтении/записи [58], однако основная структура их остается неизменной. Имеются процессы двух типов: процессы чтения и процессы записи. Все процессы совместно используют общий файл или переменную или элемент данных. Процессы чтения не изменяют объект в отличие от процессов записи. Таким образом, процессы записи должны взаимно исключать все другие процессы чтения и записи, в то время как несколько процессов чтения могут иметь доступ к разделяемым данным одновременно. Задача состоит в определении структуры управления, которая не приведет к тупику и не допустит нарушения критерия взаимного исключения.

На рис. 3.33 иллюстрируется решение задачи в том случае, когда количество процессов чтения ограничено величиной п. Если в системе количество процессов чтения не ограничено, то только п процессов могут выполняться в одно и то же время.

Проблема возникает в том случае, если количество процессов чтения не ограничено и мы хотим предоставить возможность не ограниченному количеству процессов читать одновременно.

Рис. 3.33. Задача о чтении/записи в случае, когда число процессов чтения ограничено величиной и. Первоначально имеются s процессов чтения и t процессов записи.

38.Модель сети Петри производителя-потребителя.

В задаче о производителе/потребителе также присутствует совместно используемый объект, но в этом случае разделяемый объект точно определен и является буфером. Процесс-производитель создает объекты, которые помещаются в буфер. Потребитель ждет, пока объект не будет помещен в буфер, удаляет его оттуда и использует. Такая ситуация может быть промоделирована сетью Петри так, как показано на рис. 3.29. Позиция В представляет собой буфер, каждая фишка соответствует элементу данных, который произведен, но еще не использован.

Один из вариантов этой задачи — это задача о нескольких производителях/нескольких потребителях. В этом случае несколько производителей порождают элементы данных, помещаемые в общий буфер, для нескольких потребителей. На рис. 3.30 представлено решение этой задачи в виде сети Петри. Эта сеть совпадает с сетью на рис. 3.29, за исключением того, что для представления s производителей и t потребителей мы начали выполнение сети с s фишками в начальной позиции процесса-производителя и t фишками в начальной позиции процесса-потребителя. Таким образом мы представляем s производителей и t потребителей, реализуемых реентерабельными совместно используемыми программами. Альтернативой было бы дублирование программного кода для процессов производителя и потребителя, однако результатом этого при том же самом поведении была бы гораздо большая сеть.

Рис. 3.29. Задача о производителе/потребителе, моделируемая сетью Петри.

Рис. 3.30. Задача о нескольких производителях/нескольких потребителях (s производителей и t потребителей для фиксированных s и t).

Рис. 3.31. Задача о производителе/потребителе с ограниченным буфером. Буфер, представленный позициями В и В’, ограничен п ячейками.

В другом варианте задачи о производителе/потребителе используется буфер ограниченного размера. При такой постановке задачи буфер между производителем и потребителем ограничен, т. е. имеет только n ячеек для элементов данных. Следовательно, производитель не может постоянно работать с той скоростью, которая ему нужна, а вынужден ждать, если потребитель работает медленно и буфер заполнен. На рис. 3.31 показано решение этой проблемы. Ограниченному буферу сопоставляются две позиции: В представляет количество элементов данных, которые произведены, но еще не использованы (число заполненных ячеек), В’ — количество пустых ячеек в буфере. Первоначально В’ имеет п фишек, а В фишек не имеет. Если буфер заполнен, то В’ фишек не имеет, а В имеет п фишек. Если теперь производитель попытается поместить еще один элемент данных в буфер, то он будет остановлен, так как в В’ нет фишки, делающей этот переход разрешенным.

39. Уровни активности в сетях Петри

Причиной рассмотрения сохранения в сети Петри было распределение ресурсов в операционной системе ЭВМ. Другая задача, которая может возникнуть при распределении ресурсов вычислительной системы — тупики. Тупики служат предметом многих исследований в области вычислительной техники [119]. Лучше всего иллюстрирует задачу простой пример. Рассмотрим систему, включающую два различных ресурса q и r и два процесса а и b. Если оба процесса нуждаются в обоих ресурсах, им необходимо будет совместно использовать ресурсы. Для выполнения этого потребуем, чтобы каждый процесс запрашивал ресурс, а затем освобождал его. Теперь предположим, что процесс а сначала запрашивает ресурс q, затем ресурс r и, наконец, освобождает и q, и r. Процесс b работает аналогично, но сначала запрашивает r, а затем q. Сеть Петри на рис. 4.6 иллюстрирует два процесса и распределение ресурсов между ними.

Рис. 4.6. Распределение ресурсов для случая двух процессов (а и b ) и двух ресурсов q (моделируется p4) и r (моделируется р₅ ).

Тупик в сети Петри — это переход (или множество переходов), которые не могут быть запущены. В сети Петри на рис. 4.6. тупик возникает, если нельзя запустить переходы t₂ и t₅. Переход называется активным, если он не заблокирован (не тупиковый). Это не означает, что переход разрешен, скорее он может быть разрешенным. Переход t_j сети Петри С называется потенциально запустимым в маркировке μ, если существует маркировка μ’ Є R(C, μ), в которой t_j разрешен. Переход активен в маркировке μ, если потенциально запустим во всякой маркировке из R(C, μ). Следовательно, если переход активен, то всегда возможно перевести сеть Петри из ее текущей маркировки в маркировку, в которой запуск перехода станет разрешенным.

Существуют другие, связанные с активностью понятия, которые рассматривались при изучении тупиков [53]. Их можно разбить на категории по уровню активности и определить для сети Петри С с маркировкой μ следующим образом:

Уровень 0: Переход t_j обладает активностью уровня 0, если он никогда не может быть запущен.

Уровень 1: Переход t_j обладает активностью уровня 1, если ‘ он потенциально запустим, т. е. если существует такая μ’ Є R(C, μ), что t_j разрешен в μ‘.

Уровень 2: Переход t_j обладает активностью уровня 2, если для всякого целого п существует последовательность запусков, в которой t_j присутствует по крайней мере n раз.

Уровень 3: Переход t_j обладает активностью уровня 3, если существует бесконечная последовательность запусков, в которой t_j присутствует неограниченно часто.

Уровень 4: Переход t_j обладает активностью уровня 4, если для всякой μ’ Є R(C, μ) существует такая последовательность запусков о, что t_j разрешен в δ(μ’, δ).

40. Дерево достижимости на сетях Петри

Дерево достижимости

Дерево достижимости представляет множество достижимости сети Петри. Рассмотрим, например, маркированную сеть Петри на рис. 4.9. Начальная маркировка ее — (1, 0, 0). В этой начальной маркировке разрешены два перехода: t₁ и t₂. Поскольку мы хотим рассмотреть все множества достижимости, определим новые вершины в дереве достижимости 1 ) для (достижимых) маркировок, получающихся в результате запуска каждого из этих двух переходов. Дуга, помеченная запускаемым переходом, приводит из начальной маркировки к каждой из новых маркировок (рис. 4.10).

Это (частичное) дерево показывает все маркировки, непосредственно достижимые из начальной маркировки.

Теперь необходимо рассмотреть все маркировки, достижимые из новых маркировок. Из маркировки (1,1,0) можно снова запустить t₁ (получая 1, 2, 0) и t₂ (получая (0, 2, 1)); из (0, 1, 1) можно запустить t₃ (получая (0, 0, 1)). Это порождает дерево, изображенное на рис. 4.11. Начиная с трех новых маркировок, необходимо повторить этот процесс, порождая новые маркировки, которые нужно ввести в дерево, как показано на рис. 4.12. Заметим, что маркировка (0, 0, 1) пассивная; никакой переход в ней не является разрешенным, поэтому никакие новые маркировки из этой пассивной маркировки в дереве порождаться не будут.

Рис. 4.9. Маркированная сеть Петри Рис. 4.10. Первый шаг построения, для которой строится дерева достижимости.

Кроме того, необходимо отметить, что маркировка (0, 1, 1), порождаемая запуском t₃ в (0, 2, 1), была уже порождена непосредственно из начальной маркировки запуском t₂.

Рис. 4.11. Второй шаг построения дерева достижимости.

Рис. 4.12. Третий шаг построения дерева достижимости.

Если эту процедуру повторять снова и снова, каждая достижимая маркировка окажется порожденной. Однако получившееся дерево достижимости может оказаться бесконечным. Будет порождена каждая маркировка из множества достижимости, поэтому для любой сети Петри с бесконечным множеством достижимости соответствующее дерево также должно быть бесконечным. Даже сеть Петри с конечным множеством достижимости может иметь бесконечное дерево (рис. 4.13). Дерево представляет все возможные последовательности запусков переходов. Всякий путь в дереве, начинающийся в корне, соответствует допустимой последовательности переходов. Для превращения дерева в полезный инструмент анализа необходимо найти средства ограничения его до конечного размера. (Заметим, что если какое-то представление бесконечного множества конечно, то бесконечное множество маркировок должно отображаться в такое представление. В общем случае это приведет к потере информации и, возможно, к тому, что некоторые свойства сетей Петри определить будет нельзя, но все зависит от того, как представление было получено.)

• Рис. 4.13. Простая сеть Петри с бесконечным деревом достижимости.

Для сведения дерева достижимости к конечному представлению используется еще одно средство. Рассмотрим последовательность запусков переходов а, начинающуюся в начальной маркировке ( μ и кончающуюся в маркировке μ’, μ’ > μ. Маркировка μ‘ совпадает с маркировкой μ, за исключением того, что имеет некоторые «дополнительные» фишки в некоторых позициях, т. е. μ‘ = μ + (μ’ — μ,) и (μ’ — ψ) > 0. Теперь, поскольку на запуски переходов лишние фишки не влияют, последовательность а можно запустить снова, начиная в μ’, приходя к маркировке μ» Так как действие последовательности переходов о добавило μ‘ — μ фишек к маркировке μ, она добавит также μ’ — μ, фишек и к маркировке μ‘, поэтому μ» = μ’ + (μ’ — μ) или μ» = μ + 2(μ’ — μ). В общем можно запустить последовательность а п раз, получив в результате Маркировку μ + n(μ’ — μ). Следовательно, для тех позиций, которые увеличивают число фишек последовательностью а, можно создать произвольно большое число фишек, просто повторяя последовательность о столько, сколько это нужно. В сети Петри на рис. 4.9, например, можно запустить переход t₁. столько раз, сколько необходимо для того, чтобы получить произвольное число фишек в p₂.и r. Представим бесконечное число маркировок, получающихся из циклов такого типа, с помощью специального символа ω, который обозначает «бесконечность». Для любого постоянного а определим ω + a =ω, а

Для построения дерева достижимости необходимы только эти операции над μ. Теперь можно точно сформулировать действительный алгоритм построения дерева достижимости. Каждая вершина i дерева связывается с расширенной маркировкой μ[i]; в расширенной маркировке число фишек в позиции может быть либо неотрицательным целым, либо ω. Каждая вершина классифицируется или как граничная вершина, терминальная вершина, дублирующая вершина, или как внутренняя вершина. Граничными являются вершины, которые еще не обработаны алгоритмом; алгоритм превратит их в терминальные, дублирующие или внутренние вершины.

Алгоритм начинает с определения начальной маркировки корнем дерева, т. е. граничной вершиной. До тех пор пока имеются граничные вершины, они обрабатываются алгоритмом.

Рис. 4.14. Дерево достижимости сети Петри, приведенной из рис. 4.9.

41. Классификации Базу

На первом этапе мы определяем, какой уровень параллелизма используется в вычислительной системе. Одна и та же операция может одновременно выполняться над целым набором данных, определяя параллелизм на уровне данных (обозначается буквой D на рисунке). Способность выполнять более одной операции одновременно говорит о параллелизме на уровне команд (буква O на рисунке). Если же компьютер спроектирован так, что целые последовательности команд могут быть выполнены одновременно, то будем говорить о параллелизме на уровне задач (буква T).

Второй уровень в классификационном дереве фиксирует метод реализации алгоритма. С появлением сверхбольших интегральных схем (СБИС) стало возможным реализовывать аппаратно не только простые арифметические операции, но и алгоритмы целиком. Например, быстрое преобразование Фурье, произведение матриц и LU-разложение относятся к классу тех алгоритмов, которые могут быть эффективно реализованы в СБИС’ах. Данный уровень классификации разделяет системы с аппаратной реализацией алгоритмов (буква C на схеме) и системы, использующие традиционный способ программной реализации (буква P).

Третий уровень конкретизирует тип параллелизма, используемого для обработки инструкций машины: конвейеризация инструкций (P_i) или их независимое (параллельное) выполнение (P_a). В большей степени этот выбор относится к компьютерам с программной реализацией алгоритмов, так как аппаратная реализация всегда предполагает параллельное исполнение команд.

Последний уровень данной классификации определяет способ управления, принятый в вычислительной системе: синхронный (S) или асинхронный (A). Если выполнение команд происходит в строгом порядке, определяемом только сигналами таймера и счетчиком команд, то будем говорить о синхронном способе управления. Если же для инициации команды определяющими являются такие факторы, как, например, готовность данных, то попадаем в класс машин с асинхронным управлением.

Модель сети Петри для спящего брадобрея

Источник