что такое сектор круга
Что такое сектор круга
Круг — это часть плоскости, ограниченная окружностью. Центр данной окружности называется центром круга, а расстояние от центра до любой точки окружности — радиусом круга:
O — центр круга, OA — радиус круга.
Площадь круга
Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга:
где S — площадь круга, а r — радиус круга.
Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:
| D = 2r, значит r = | D | . |
| 2 |
Следовательно, формула нахождения площади круга через диаметр будет выглядеть так:
| S = π( | D | ) 2 = π | D 2 | = π | D 2 | . |
| 2 | 2 2 | 4 |
Сектор круга. Площадь сектора
Сектор — это часть круга, ограниченная двумя радиусами и дугой. Два радиуса разделяют круг на два сектора:
Чтобы найти площадь сектора, дуга которого содержит n°, надо площадь круга разделить на 360 и полученный результат умножить на n.
Формула площади сектора:
| S = | πr 2 | · n = | πr 2 n | , |
| 360 | 360 |
где S — площадь сектора. Выражение
можно представить в виде произведения
| πr 2 n | = n · | πr | · | r | , |
| 360 | 180 | 2 |
| где | nπr | — это длина дуги сектора. |
| 180 |
Следовательно, площадь сектора равна длине дуги сектора, умноженной на половину радиуса:
где S — это площадь сектора, s — длина дуги данного сектора, r — радиус круга.
Сегмент. Площадь сегмента
Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой. Любая хорда делит круг на два сегмента:
Площадь сегмента равна половине радиуса, умноженной на разность между дугой сегмента и половиной хорды двойной дуги.
Площадь сегмента AMB будет вычисляться по формуле:
где S — это площадь сегмента, r — радиус круга, s — длина дуги AB, а BC — длина половины хорды двойной дуги.
Геометрия. Урок 5. Окружность
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Определение окружности
Окружность – геометрическое место точек, равноудаленных от данной точки.
Отрезки в окружности
Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.
Хорда a – отрезок, соединяющий две точки на окружности.
Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).
O A – радиус, D E – хорда, B C – диаметр.
Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.
Касательная к окружности – прямая, имеющая с окружностью одну общую точку.
Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.
Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).
Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.
Дуга в окружности
Теорема 4:
Равные хорды стягивают равные дуги.
Углы в окружности
В окружности существует два типа углов: центральные и вписанные.
Центральный угол – угол, вершина которого лежит в центре окружности.
∠ A O B – центральный.
Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.
Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.
∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2
∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °
Длина окружности, длина дуги
Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.
Длина окружности находится по формуле:
Площадь круга и его частей
Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.
Круг – часть пространства, которая находится внутри окружности.
Иными словами, окружность – это граница, а круг – это то, что внутри.
Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.
Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.
Площадь круга находится по формуле: S = π R 2
Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Примеры сектора в реальной жизни: кусок пиццы, веер.
Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α
Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.
Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.
Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.
S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α
Теорема синусов
Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с окружностями.
Сектор (геометрия)
Сектор в геометрии — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Свойства
См. также
Полезное
Смотреть что такое «Сектор (геометрия)» в других словарях:
Сегмент (геометрия) — У этого термина существуют и другие значения, см. Сегмент. Сегмент круга закрашен жёлтым цветом Сегмент плоская фигура, заключённая между кривой и её хордой. Как частный сл … Википедия
Жёсткий диск — Запрос «HDD» перенаправляется сюда; см. также другие значения … Википедия
Польша — (Polska) Польская Народная Республика (Polska Rzeczpospolita Ludowa), ПНР. I. Общие сведения П. социалистическое государство в Центральной Европе, в бассейне рр. Висла и Одра, между Балтийским морем на С., Карпатами и… … Большая советская энциклопедия
БЕСКОНЕЧНО МАЛЫХ ИСЧИСЛЕНИЕ — термин, ранее объединявший различные разделы математич. анализа, связанные с понятием бесконечно малой функции. Хотя метод бесконечно малых (в той или иной форме) с успехом применялся учеными Древней Греции и средневековой Европы для решения… … Математическая энциклопедия
Кравец, Торичан Павлович — В Википедии есть статьи о других людях с такой фамилией, см. Кравец. Торичан Павлович Кравец Дата рождения: 10 (22) марта 1876( … Википедия
Югославия — (Jugoslavija, Jyгославиja) Социалистическая Федеративная Республика Югославия, СФРЮ (Socialistička Federativna Republika Jugoslavija, Социjaлистичка Федеративна Република Jyгославиja). I. Общие сведения Ю.… … Большая советская энциклопедия
Цфасман, Михаил Анатольевич — В Википедии есть статьи о других людях с такой фамилией, см. Цфасман. Михаил Анатольевич Цфасман Дата рождения: 23 июля 1954(1954 07 23) (58 лет) Место рождения: Москва, СССР Страна … Википедия
Всё про окружность и круг
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
Квадрат касательной равен произведению секущей на ее внешнюю часть
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = ПR 2 а/360°.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.
Сектор окружности формулы, описание и рисунки
Изучая плоские геометрические фигуры, необходимо четко понимать все определения того или иного обозначения. Правильное их представление позволит быстро и правильно освоить предлагаемые азы теории. И так окунемся в его мир.
• Часть круга, которая ограничена двумя радиусами и дугой окружности, проведенной из одной точки радиуса в другую, будем называть сектором.
• Часть круга, которая ограничена дугой окружности, проведенной из одной точки хорды в другую, будем называть сегментом.
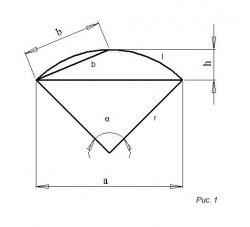
Сектор окружности и его сегмент изображены на 1-ом рисунке, где
r – радиус;
l – длина дуги;
a – хорда;
α – центральный угол (в градусах);
h – стрела сегмента;
S – площадь сектора;
S1 – площадь сегмента
a = 2√(2hr – h²) = 2r sin α/2
h = r – √(r² – a²/4) = r(1 – cos α/2) = a/2 tg α/4
l = 2πrα/360 ≈ 0.01745rα
S = πr²/360
S1 = r²/2 (2πα/180 – sin α) = ½ (lr – a(r – h))
Вспомогательные формулы
l ≈ 0,01745rα ≈ (8b – a)/3 ≈ √(a² + h²16/3)
S ≈ 0,00873r² α
S1 ≈ h/15(6a + 8b)
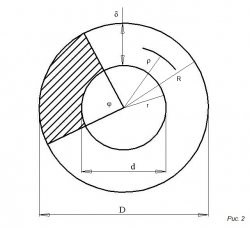
Круговое кольцо изображено на 2-ом рисунке, где
D – внутренний диаметр;
d – внешний диаметр;
R – внешний радиус;
R – внутренний ралиус;
ρ – средний радиус;
δ – толщина кольца;
S – площадь кольца;
S1 – площадь части кольца заштрихованной поверхности
D = 2R
d = 2r
ρ = ½(R + r)
δ = R – r
S = π(R² – r²) = π(D² – d²)/4 = 2πρδ
S1 = φπ(R² – r²)/360 = φπ(D² – d²)/180 = φπρδ/180
Надеемся, что полученная информация пригодится в решении различных задач и вопросов.