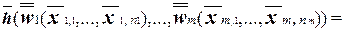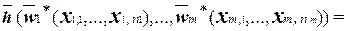что такое самодвойственная функция
Что такое самодвойственная функция
Определение. Булева функция f(x1, …, xn) самодвойственна (принадлежит классу S), если она равна двойственной себе функции, то есть
Примеры. Мажоритарная функция самодвойственна:
Из элементарных функций самодвойственными являются лишь тождественная функция и инверсия. Остальные функции, в частности, штрих Шеффера и стрелка Пирса, несамодвойственны. •
Алгоритм распознавания самодвойственной функции, заданной таблицей истинности. Очевидно, что для проверки самодвойственности булевой функции можно не получать двойственную ей функцию в явном виде, а лишь сравнивать значения исходной функции на противоположных наборах. Функция самодвойственна, если и только если на противоположных наборах принимает противоположые значения.
Достаточное условие несамодвойственности булевой функции. Если число единиц в столбце значений функции не совпадает с числом нулей, то функция не является самодвойственной.
Примеры. Рассмотрим три булевы функции.
Для функции f(x,y,z) выполняется достаточное условие несамодвойственности. Для остальных оно не выполняется, при этом функция g(x,y,z) несамодвойственна, так как на первом и последнем наборах принимает одинаковые значения, а функция h(x,y,z) самодвойственна. •
Пример. Из всех 16 булевых функций двух аргументов x1, x2 4 функции (2 2 2 –1 ) принадлежат классу S: тождественные функции x1 и x2 и их инверсии x 1 и x 2. •
Теорема о замкнутости класса S. Множество всех самодвойственных булевых функций является замкнутым классом.
Доказательство. Рассмотрим суперпозицию любых булевых функций из S, то есть функцию
и покажем, что она самодвойственна. Пользуясь принципом двойственности, получим функцию, двойственную f(x1, …, xn).
[ учтем, что каждая из функций, образующих суперпозицию, самодвойственна ]
Итак, мы показали, что f * (x1, …, xn)=f(x1, …, xn), значит, f(x1, …, xn) самодвойственна, и класс S замкнут. •
Лемма о несамодвойственной булевой функции. Если булева функция несамодвойственна, то из нее подстановкой вместо аргументов переменной x и ее инверсии x можно получить либо константу 0, либо константу 1.
Доказательство. Рассмотрим несамодвойственную булеву функцию f(x1, …, xn). Для нее существует такой набор a1… an, что
Заменим каждый аргумент xi функции f(x1, …, xn на x a i, (подстановка переменной x и ее инверсии x допустима по условию теоремы). В результате получим функцию одного аргумента
Но набор a1… an выбран так, что правые части равны, следовательно, g(0)=g(1), и константа получена. •
Примеры. Рассмотрим функцию f(y,z) = y ↓ z. Она несамодвойственна, так как на противоположных наборах 01 и 10 принимает одно и то же значение 0. В качестве набора a1a2 возьмем набор 01. Положим y=x 0 = x и z=x 1 =x, получим
Аналогично, рассмотрев функцию h(y,z)=y/z, которая на тех же противоположных наборах принимает значение 1, получим:
 Раздел 1. Математическая логика
Раздел 1. Математическая логика
 Тема 1. Логика высказываний
Тема 1. Логика высказываний
 Тема 2. Булевы функции
Тема 2. Булевы функции
В этой теме рассматриваются всюду определенные функции, заданные на множестве B=<0,1>. Такие функции называются булевыми. Основная цель темы – доказать критерий полноты класса функций – теорему Поста.
 §1. Замкнутость и полнота
§1. Замкнутость и полнота
 §2. Самодвойственные функции
§2. Самодвойственные функции
Этот и два следующих параграфа посвящены рассмотрению трех конкретных классов функций: самодвойственных, монотонных и линейных.
Определение. Функция g(x1,…,xn) называется двойственной k f(x1,…,xn), если выполняется равенство
Например, x × y двойственна x Ú y, и наоборот. Это следует из равенств x × y= n ( n (x) Ú n (y) и x Ú y= n ( n (x) × n (y)), которые мы уже приводили. Функция x ® y двойственна функции n (x)&y, поскольку n ( n (x) ® n (y)= n [ n ( n (x)) Ú n (y)]= n (x Ú n (y)) = n (x)&y. Отметим, что первое равенство выполняется на основании закона 20, второе 19 и третье 18 и 19.
Определение. Функция f(x1,…,xn) называется самодвойственной, если выполняется равенство
Другими словами, функция самодвойственна, если она совпадает со своей двойственной.
Приведем примеры. Легко видеть, что самодвойственными функциями являются тождественная функция и отрицание: n [ e ( n (x))]= n [ n (x)]=x= e (x), n [ n ( n (x))]= n (x). В то же время, произведение x × y самодвойственной не является, поскольку двойственно дизъюнкции x Ú y и x × y ¹ x Ú y. Можно показать, что никакая функция от двух переменных, существенно зависящая от каждого аргумента, самодвойственной не является. В качестве еще одного примера самодвойственной функции приведем функцию
| Действительно, n [f( n (x1), n (x2), n (x3)]= | |
| = n [ n (x1) × n (x2)) Ú ( n (x1) × n (x3)) Ú ( n (x2) × n (x3))]= | |
| = n [ n (x1 Ú x2) Ú n (x1 Ú x3)) Ú n (x2 Ú x3)]= | |
| =(x1 Ú x2) × (x1 Ú x3) × (x2 Ú x3)= | |
| =(x1 × x1 × x2) Ú (x1 × x1 × x3) Ú (x1 × x3 × x2) Ú (x1 × x3 × x3) Ú | |
| Ú (x2 × x1 × x2) Ú (x2 × x1 × x3) Ú (x2 × x3 × x2) Ú (x2 × x3 × x3)= | |
| =(x1 × x2) Ú (x1 × x3) Ú (x1 × x2 × x3) Ú (x1 × x3) Ú | |
| Ú (x1 × x2) Ú (x1 × x2 × x3) Ú (x2 × x3) Ú (x2 × x3)= | |
| =(x1 × x2) Ú (x1 × x3) Ú (x2 × x3) Ú (x1 × x2 × x3)= | |
| =(x1 × x2) Ú (x1 × x3) Ú (x2 × x3). | |
Последнее равенство выполняется на основании закона поглощения.
Отметим, что равенство (1) из определения самодвойственности равносильно равенству n (f(x1,…,xn))=f( n (x1),…, n (xn)). (2)
Класс всех самодвойственных функций обозначим буквой S. Убедимся в том, что S – замкнутый класс. Как уже отмечалось, S содержит e (x). Пусть f(x1,…,xn) Î S и y1,…,yn – новый набор переменных. Тогда поскольку равенство f(x1,…,xn)= n [f( n (x1),…, n (xn)] выполняется для всех значений переменных x1,…,xn, то n [f( n (y1),…, n (yn)]=f(y1,…,yn). Следовательно, f(y1,…,yn) Î S и S – замкнут относительно переименования аргументов. Возьмем теперь функции f(x1,…,xk), g1(x1,…,xn),…, gk(x1,…,xn) из S. Поскольку эти функции принадлежат S, то, используя равенство (2), получаем, что
| Тогда если h(x1. xn)=f(g1(x1,…,xn),…,gk(x1. xn)),то | |
| h( n (x1),…, n (xn))= | |
| =f[g1( n (x1),…, n (xn)),…,g( n (x1),…, n (xn))]= | |
| =f[ n (g1(x1,…,xn)),…, n (gk(x1,…,xn))]= | |
| = n [f(g1(x1,…,xn),…,gk(x1,…,xn))]= | |
| = n (h(x1,…,xn)). | |
В силу равенства (2), h(x1,…,xn) – самодвойственная функция. Следовательно, класс S замкнут относительно суперпозиции.
Следующее утверждение называется леммой о несамодвойственной функции.
Лемма. Пусть f(x1,…,xn) – несамодвойственная функция. Тогда замыкание класса K=
Доказательство. Поскольку f(x1,…,xn) – несамодвойственная функция, то существуют a1,…,an Î B такие, что
Множество B содержит только два элемента. Поэтому из этого неравенства следует равенство
Для удобства обозначений предположим, что a1,…,ak=0, ak+1,…, an=1. Тогда последнее равенство можно записать так:
где точка с запятой отделяет k-ый аргумент от (k+1)-го.
Заметим, что g(x) принадлежит [K]. Имеем равенства
Следовательно, g(x) – одна из констант, принадлежащая [K]. Поскольку K содержит отрицание, то и другая константа принадлежит [K].
В заключение параграфа рассмотрим пример решения задачи на распознавание самодвойственности: определить, будет ли функция f(x1,x2)=x2 × (x2 ® x1) самодвойственной? (Впрочем, мы уже знаем, что f(x1,x2) несамодвойственна, но надо это доказать). Для получения ответа на вопрос составим таблицу, задающую функции f(x1,x2) и n (f( n (x1), n (x2)). (см. таблицу 2.4)
| x1 | x2 | x2 ® x1 | n (x2) | n (x2) ® n (x1) | f(x1,x2) | n (f( n (x1), n (x2)) |
| 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 | 1 | 1 |
Мы видим, что f(x1,x2) ¹ n (f( n (x1), n (x2)), например при x1=0, x2=1. Следовательно, функция f(x1,x2) самодвойственной не является. (Для того, чтобы сделать заключение о несамодвойственности, можно было, конечно, прервать составление таблицы на второй строке.
 §3. Монотонные функции
§3. Монотонные функции
 §4. Линейные функции
§4. Линейные функции
 §5. Критерий полноты
§5. Критерий полноты
 Задачи
Задачи
 Ответы, указания и решения
Ответы, указания и решения
 Тема 3. Логика предикатов
Тема 3. Логика предикатов
 Тема 4. Метод резолюций
Тема 4. Метод резолюций
 Раздел 2. Теория графов
Раздел 2. Теория графов
САМОДВОЙСТВЕННЫЕ ФУНКЦИИ
СПЕЦИАЛЬНЫЕ КЛАССЫ БУЛЕВСКИХ
ФУНКЦИЙ
ОПРЕДЕЛЕНИЕ
Множество функций B 
Например, множество <x, 
ФУНКЦИИ, СОХРАНЯЮЩИЕ НОЛЬ
Обозначим как Т0 множество всех таких булевских функций, которые на нулевом наборе значений переменных принимают значение 0.
О таких функциях говорят, что они сохраняют 0, т.е. множество б.ф., сохраняющих ноль, это:
Т0 = <f(x1. x n) ½ f(0. 0) = 0>.
Сформулируем простейшие свойства класса T0.
1. Класс T0 является замкнутым классом функций.
Проведем обоснование этого свойства в соответствии с определением понятия формулы над классом функций.
ФУНКЦИИ, СОХРАНЯЮЩИЕ ЕДИНИЦУ
Класс T1 является замкнутым и содержит 
САМОДВОЙСТВЕННЫЕ ФУНКЦИИ
Двоичные наборы 

Противоположные наборы значений переменных в табличном задании булевых функций соответствуют строкам, расположенным симметрично относительно середины таблицы.
Тогда, пусть 

ОПРЕДЕЛЕНИЕ
Двойственная функция к заданной функции f обозначается как f*.
Нетрудно проверить, что 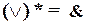
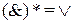

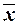
Кроме того, легко убедиться в справедливости следующего свойства: функция, двойственная к двойственной функции, совпадает с исходной функцией, т.е. справедливо равенство: f** = f.
ОПРЕДЕЛЕНИЕ
Функция f называется самодвойственной, если f = f*.
То есть всякая самодвойственная функция на любых двух противоположных наборах значений переменных принимает противоположные значения. Примерами самодвойственных функций являются тождественная функция f(x) = x и отрицание f(x) = 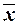
Множество всех самодвойственных функций обозначается как S.
Установленное ранее свойство симметричности расположения противоположных наборов в табличном задании булевских функций позволяет использовать следующую схему построения табличного задания функции, двойственной к заданной функции.
1. Выпишем столбец значений f в обратном порядке.
2. В полученном столбце выполним замену всякого значения в нем на противоположное значение.
Если функция f задана формулой, то для получения формульного представления функции f* можно воспользоваться следующей теоремой.
ТЕОРЕМА 4.7 (О формуле для двойственной функции)
Доказательство
Докажем теорему индукцией по глубине формулы U.
1. Базис индукции.Покажем, что если f = 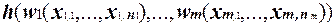
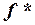

=
=
= 
2. Индуктивное предположение. Предположим, что доказываемое в свойство выполняется для всех формул, глубина которых не превосходит n.
Тогда аналогично доказательству базиса индукции можно показать, что 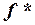
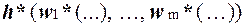
Поскольку всякая функция 
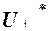


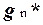
Презентация по математической логике на тему «Двойственные функции»
Описание презентации по отдельным слайдам:
Двойственные функции Булевы функции
Двойственные функции Булева функция f*(x1, …, xn) называется двойственной булевой функции f(x1, …, xn), если она получена из f(x1, …, xn) инверсией всех аргументов и самой функции, то есть
Пример Построим функцию, двойственную стрелке Пирса. Значения двойственной функции можно получить переворотом и инверсией столбца значений исходной функции
Пример. Покажем, что дизъюнкция двойственна конъюнкции (применив законы де Моргана и двойного отрицания):
Двойственная формула Определение Формула F* называется двойственной формуле F, если она получена из F заменой символов функций на символы двойственных им функций. Пример
Пример Рассмотрим формулу задающую булеву функцию НЕ-ИЛИ, то есть стрелку Пирса. Двойственная ей формула должна задавать функцию, двойственную стрелке Пирса – это штрих Шеффера: в самом деле это функция НЕ-И, то есть штрих Шеффера.
Самодвойственная функция Функция, совпадающая со своей двойственной, называется самодвойственной. F*=F Следствие из принципа двойственности. Если формулы F1 и F2 равносильны, то двойственные им формулы F*1 и F*2, также равносильны.
Способы получения двойственной функции – по определению двойственной функции – инверсией в формуле Ff всех аргументов и самой функции; – по определению двойственной формулы и принципу двойственности – заменой в формуле Ff символов функций на символы двойственных им функций; – построением таблицы истинности исходной функции по заданной формуле Ff, а затем переходом к таблице истинности двойственной функции (переворотом и инверсией столбца значений исходной функции).
Упражнение 1 Построить формулы для функций, двойственных данным, пользуясь двумя разными способами: определением двойственной функции и принципом двойственности. Сравнить таблицы истинности, построенные по полученным формулам.
Упражнение 2 Двойственны ли формулы Ff и Gg? Функции f и g?
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-011113
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
Минпросвещения предлагает закрыть пляжи детских лагерей для посторонних лиц
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
В Псковской области ввели обязательную вакцинацию для студентов
Время чтения: 1 минута
Школьники из России выиграли 8 медалей на Международном турнире по информатике
Время чтения: 3 минуты
ОНФ проверит качество охраны в российских школах
Время чтения: 2 минуты
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

 Раздел 1. Математическая логика
Раздел 1. Математическая логика Тема 1. Логика высказываний
Тема 1. Логика высказываний